Empíricamente, hemos visto que la regularización ayuda a reducir el reciclaje. Esto es inspirador, pero, desafortunadamente, no es obvio por qué ayuda la regularización. Por lo general, las personas lo explican de alguna manera: en cierto sentido, los pesos más pequeños tienen menos complejidad, lo que proporciona una explicación más simple y más eficiente de los datos, por lo que deberían preferirse. Sin embargo, esta es una explicación demasiado corta, y algunas partes pueden parecer dudosas o misteriosas. Desplieguemos esta historia y examinémosla con ojo crítico. Para hacer esto, supongamos que tenemos un conjunto de datos simple para el que queremos crear un modelo:

En términos de significado, aquí estudiamos el fenómeno del mundo real, y x e y denotan datos reales. Nuestro objetivo es construir un modelo que nos permita predecir y en función de x. Podríamos intentar usar una red neuronal para crear dicho modelo, pero sugiero algo más simple: intentaré modelar y como un polinomio en x. Haré esto en lugar de las redes neuronales, ya que el uso de polinomios hace que la explicación sea especialmente clara. Tan pronto como tratemos el caso del polinomio, pasaremos a la Asamblea Nacional. Hay diez puntos en el gráfico anterior, lo que significa que podemos
encontrar un polinomio único de noveno orden y = a
0 x
9 + a
1 x
8 + ... + un
9 que se ajusta exactamente a los datos. Y aquí está el gráfico de este polinomio.
Golpe perfecto. Pero podemos obtener una buena aproximación usando el modelo lineal y = 2x
Cual es mejor? ¿Cuál es más probable que sea cierto? ¿Cuál se generalizará mejor a otros ejemplos del mismo fenómeno del mundo real?
Preguntas difíciles Y no se pueden responder exactamente sin información adicional sobre el fenómeno subyacente del mundo real. Sin embargo, veamos dos posibilidades: (1) un modelo con un polinomio de noveno orden realmente describe el fenómeno del mundo real y, por lo tanto, se generaliza perfectamente; (2) el modelo correcto es y = 2x, pero tenemos ruido adicional asociado con el error de medición, por lo que el modelo no encaja perfectamente.
A priori, no se puede decir cuál de las dos posibilidades es correcta (o si no hay una tercera). Lógicamente, cualquiera de ellos puede ser cierto. Y la diferencia entre ellos no es trivial. Sí, según los datos disponibles, se puede decir que solo hay una ligera diferencia entre los modelos. Pero supongamos que queremos predecir el valor de y correspondiente a algún valor grande de x, mucho más grande que cualquiera de los que se muestran en el gráfico. Si intentamos hacer esto, aparecerá una gran diferencia entre las predicciones de los dos modelos, ya que el término x
9 domina en el polinomio de noveno orden, y el modelo lineal sigue siendo lineal.
Un punto de vista sobre lo que está sucediendo es afirmar que, si es posible, se debe usar una explicación más simple en la ciencia. Cuando encontramos un modelo simple que explica muchos puntos de referencia, solo queremos gritar: "¡Eureka!" Después de todo, es poco probable que aparezca una explicación simple por casualidad. Sospechamos que el modelo debería producir alguna verdad asociada con el fenómeno. En este caso, el modelo y = 2x + ruido parece mucho más simple que y = a
0 x
9 + a
1 x
8 + ... Sería sorprendente si la simplicidad surgiera por casualidad, por lo que sospechamos que y = 2x + ruido expresa algo verdad subyacente Desde este punto de vista, el modelo de noveno orden simplemente estudia el efecto del ruido local. Aunque el modelo de noveno orden funciona perfectamente para estos puntos de referencia específicos, no puede generalizarse a otros puntos, como resultado de lo cual el modelo lineal con ruido tendrá mejores capacidades predictivas.
Veamos qué significa este punto de vista para las redes neuronales. Supongamos que, en nuestra red, existen principalmente pesos bajos, como suele ser el caso en las redes regularizadas. Debido a su pequeño peso, el comportamiento de la red no cambia mucho cuando se cambian varias entradas aleatorias aquí y allá. Como resultado, la red regularizada es difícil de aprender los efectos del ruido local presente en los datos. Esto es similar al deseo de garantizar que la evidencia individual no afecte en gran medida la salida de la red en su conjunto. En cambio, la red regularizada está capacitada para responder a la evidencia que a menudo se encuentra en los datos de capacitación. Por el contrario, una red con grandes pesos puede cambiar su comportamiento con bastante fuerza en respuesta a pequeños cambios en los datos de entrada. Por lo tanto, una red irregular puede usar grandes pesos para entrenar un modelo complejo que contiene mucha información de ruido en los datos de entrenamiento. En resumen, las limitaciones de las redes regularizadas les permiten crear modelos relativamente simples basados en patrones que a menudo se encuentran en los datos de entrenamiento, y son resistentes a las desviaciones causadas por el ruido en los datos de entrenamiento. Existe la esperanza de que esto haga que nuestras redes estudien el fenómeno en sí y generalicen mejor el conocimiento adquirido.
Dicho todo esto, la idea de dar preferencia a explicaciones más simples debería ponerlo nervioso. A veces las personas llaman a esta idea "la navaja de afeitar de Occam" y la aplican celosamente, como si tuviera el estatus de un principio científico general. Pero esto, por supuesto, no es un principio científico general. No hay una razón lógica a priori para preferir explicaciones simples a las complejas. A veces una explicación más complicada es correcta.
Permítanme describir dos ejemplos de cómo una explicación más compleja resultó ser correcta. En la década de 1940, el físico Marcel Shane anunció el descubrimiento de una nueva partícula. La compañía para la que trabajó, General Electric, estaba encantada y distribuyó ampliamente la publicación de este evento. Sin embargo, el físico Hans Bethe se mostró escéptico. Bethe visitó a Shane y estudió las placas con rastros de la nueva partícula de Shane. Shane mostró Beta placa tras placa, pero Bete encontró en cada una de ellas un problema que indicaba la necesidad de rechazar estos datos. Finalmente, Shane le mostró a Beta un registro que parecía adecuado. Bethe dijo que probablemente era solo una desviación estadística. Shane: "Sí, pero las posibilidades de que se deba a estadísticas, incluso según su propia fórmula, son una de cada cinco". Bethe: "Sin embargo, ya he visto cinco registros". Finalmente, Shane dijo: "Pero usted explicó cada uno de mis registros, cada buena imagen con alguna otra teoría, y tengo una hipótesis que explica todos los registros a la vez, de lo que se deduce que estamos hablando de una nueva partícula". Bethe respondió: “La única diferencia entre mis explicaciones y las tuyas es que las tuyas están equivocadas y las mías son correctas. Tu única explicación es incorrecta, y todas mis explicaciones son correctas. Posteriormente, resultó que la naturaleza estaba de acuerdo con Bethe, y la partícula de Shane se evaporó.
En el segundo ejemplo, en 1859, el astrónomo Urbain Jean Joseph Le Verrier descubrió que la forma de la órbita de Mercurio no se corresponde con la teoría de la gravitación universal de Newton. Hubo una pequeña desviación de esta teoría, y luego se propusieron varias opciones para resolver el problema, que se redujo al hecho de que la teoría de Newton en su conjunto es correcta y requiere solo un ligero cambio. Y en 1916, Einstein demostró que esta desviación puede explicarse bien utilizando su teoría general de la relatividad, radicalmente diferente de la gravedad newtoniana y basada en matemáticas mucho más complejas. A pesar de esta complejidad adicional, hoy se acepta generalmente que la explicación de Einstein es correcta y que la gravedad newtoniana es incorrecta
incluso en una forma modificada . Esto sucede, en particular, porque hoy sabemos que la teoría de Einstein explica muchos otros fenómenos con los que la teoría de Newton tuvo dificultades. Además, aún más sorprendente, la teoría de Einstein predice con precisión varios fenómenos que la gravedad newtoniana no predijo en absoluto. Sin embargo, estas cualidades impresionantes no eran obvias en el pasado. A juzgar por la simple simplicidad, alguna forma modificada de la teoría newtoniana habría parecido más atractiva.
Se pueden extraer tres moralidades de estas historias. Primero, a veces es bastante difícil decidir cuál de las dos explicaciones será "más fácil". En segundo lugar, incluso si tomamos esa decisión, ¡la simplicidad debe guiarse con extremo cuidado! En tercer lugar, la verdadera prueba del modelo no es la simplicidad, sino qué tan bien predice nuevos fenómenos en nuevas condiciones de comportamiento.
Teniendo en cuenta todo esto y teniendo cuidado, aceptaremos un hecho empírico: los NS regularizados generalmente están mejor generalizados que los irregulares. Por lo tanto, más adelante en el libro usaremos la regularización. Las historias mencionadas solo son necesarias para explicar por qué nadie ha desarrollado una explicación teórica completamente convincente de por qué la regularización ayuda a las redes a generalizarse. Los investigadores continúan publicando trabajos donde intentan probar diferentes enfoques para la regularización, compararlos, ver qué funciona mejor y tratar de entender por qué los diferentes enfoques funcionan peor o mejor. Entonces la regularización puede ser tratada como una
nube . Cuando ayuda bastante a menudo, no tenemos una comprensión sistémica completamente satisfactoria de lo que está sucediendo, solo reglas heurísticas y prácticas incompletas.
Aquí yace un conjunto más profundo de problemas que van al corazón de la ciencia. Este es un problema de generalización. La regularización puede darnos una varita mágica computacional que ayuda a nuestras redes a generalizar mejor los datos, pero no brinda una comprensión básica de cómo funciona la generalización y cuál es el mejor enfoque para ella.
Estos problemas se remontan al
problema de la inducción , cuya interpretación conocida fue realizada por el filósofo escocés
David Hume en el libro "
A Study on Human Cognition " (1748). El problema de la inducción es el tema del "
teorema sobre la ausencia de comidas gratuitas " de
David Walpert y William Macredie (1977).
Y esto es especialmente molesto, porque en la vida cotidiana las personas son fenomenalmente capaces de generalizar los datos. Muestre algunas imágenes del elefante al niño, y él aprenderá rápidamente a reconocer a otros elefantes. Por supuesto, a veces puede cometer un error, por ejemplo, confundir un rinoceronte con un elefante, pero en general, este proceso funciona sorprendentemente con precisión. Ahora, tenemos un sistema, el cerebro humano, con una gran cantidad de parámetros libres. Y después de que se le muestre una o más imágenes de entrenamiento, el sistema aprende a generalizarlas a otras imágenes. ¡Nuestro cerebro, en cierto sentido, es increíblemente bueno para regularizar! ¿Pero cómo hacemos esto? Por el momento, esto es desconocido para nosotros. Creo que en el futuro desarrollaremos tecnologías de regularización más potentes en redes neuronales artificiales, técnicas que finalmente permitirán a la Asamblea Nacional generalizar datos basados en conjuntos de datos aún más pequeños.
De hecho, nuestras redes ya se están generalizando mucho mejor de lo que podría esperarse a priori. Una red con 100 neuronas ocultas tiene casi 80,000 parámetros. Tenemos solo 50,000 imágenes en datos de entrenamiento. Esto es lo mismo que tratar de estirar un polinomio de 80,000 órdenes sobre 50,000 puntos de referencia. Según todas las indicaciones, nuestra red debe volverse a entrenar terriblemente. Y, sin embargo, como hemos visto, una red de este tipo en realidad se generaliza bastante bien. ¿Por qué está pasando esto? Esto no está del todo claro. Se
planteó la
hipótesis de que "la dinámica del aprendizaje por descenso de gradiente en redes multicapa está sujeta a autorregulación". Esta es una fortuna extrema, pero también un hecho bastante inquietante, ya que no entendemos por qué sucede esto. Mientras tanto, adoptaremos un enfoque pragmático y utilizaremos la regularización siempre que sea posible. Esto será beneficioso para nuestra Asamblea Nacional.
Permítanme terminar esta sección volviendo a lo que no expliqué antes: que la regularización de L2 no limita los desplazamientos. Naturalmente, sería fácil cambiar el procedimiento de regularización para que regularice los desplazamientos. Pero empíricamente, esto a menudo no cambia los resultados de manera notable, por lo tanto, hasta cierto punto, tratar con la regularización de sesgos, o no, es una cuestión de acuerdo. Sin embargo, vale la pena señalar que un desplazamiento grande no hace que una neurona sea sensible a los insumos como los pesos grandes. Por lo tanto, no debemos preocuparnos por las grandes compensaciones que permiten que nuestras redes aprendan el ruido en los datos de entrenamiento. Al mismo tiempo, al permitir grandes desplazamientos, hacemos que nuestras redes sean más flexibles en su comportamiento, en particular, los grandes desplazamientos facilitan la saturación de las neuronas, lo que nos gustaría. Por esta razón, generalmente no incluimos compensaciones en la regularización.
Otras técnicas de regularización.
Hay muchas técnicas de regularización además de L2. De hecho, ya se han desarrollado tantas técnicas que, con todo el deseo, no podría describirlas brevemente. En esta sección, describiré brevemente otros tres enfoques para reducir el reentrenamiento: regularizar L1,
abandonar y aumentar artificialmente el conjunto de entrenamiento. No los estudiaremos tan profundamente como los temas anteriores. En cambio, solo los conocemos y, al mismo tiempo, apreciamos la variedad de técnicas de regularización existentes.
Regularización L1
En este enfoque, modificamos la función de costo irregular agregando la suma de los valores absolutos de los pesos:
Intuitivamente, esto es similar a la regularización de L2, que multas por grandes pesos y hace que la red prefiera pesos bajos. Por supuesto, el término de regularización L1 no es como el término de regularización L2, por lo que no debe esperar exactamente el mismo comportamiento. Tratemos de entender cómo el comportamiento de una red entrenada con regularización L1 difiere de una red entrenada con regularización L2.
Para hacer esto, observe las derivadas parciales de la función de costo. Diferenciando (95), obtenemos:
donde sgn (w) es el signo de w, es decir, +1 si w es positivo y -1 si w es negativo. Usando esta expresión, modificamos ligeramente la propagación hacia atrás para que realice un descenso de gradiente estocástico usando la regularización L1. La regla de actualización final para la red regularizada L1:
donde, como de costumbre, ∂C / ∂w se puede estimar opcionalmente utilizando el valor promedio del mini-paquete. Compare esto con la regla de actualización de regularización L2 (93):
En ambas expresiones, el efecto de la regularización es reducir los pesos. Esto coincide con la noción intuitiva de que ambos tipos de regularización penalizan grandes pesos. Sin embargo, los pesos se reducen de diferentes maneras. En la regularización de L1, los pesos disminuyen en un valor constante, tendiendo a 0. En la regularización de L2, los pesos disminuyen en un valor proporcional a w. Por lo tanto, cuando algo de peso tiene un gran valor | w |, la regularización de L1 reduce el peso no tanto como L2. Y viceversa, cuando | w | pequeño, la regularización de L1 reduce el peso mucho más que la regularización de L2. Como resultado, la regularización de L1 tiende a concentrar los pesos de la red en un número relativamente pequeño de enlaces de gran importancia, mientras que otros pesos tienden a cero.
Alivié un problema en la discusión anterior: la derivada parcial ∂C / ∂w no está definida cuando w = 0. Esto se debe a que la función | w | hay un "doblez" agudo en el punto w = 0, por lo tanto, no se puede diferenciar allí. Pero esto no da miedo. Solo aplicamos la regla habitual e irregular para el descenso de gradiente estocástico cuando w = 0. Intuitivamente, no hay nada de malo en eso: la regularización debería reducir los pesos, y obviamente no puede reducir los pesos que ya son iguales a 0. Más precisamente, utilizaremos las ecuaciones (96) y (97) con la condición de que sgn (0) = 0. Esto nos dará una regla conveniente y compacta para el descenso de gradiente estocástico con regularización L1.
Excepción [abandono]
Una excepción es una técnica de regularización completamente diferente. A diferencia de la regularización de L1 y L2, la excepción no trata con un cambio en la función de costo. En cambio, estamos cambiando la red misma. Permítanme explicar la mecánica básica del funcionamiento de una excepción antes de profundizar en el tema de por qué funciona y con qué resultados.
Supongamos que estamos tratando de entrenar una red:
En particular, digamos que tenemos entrada de entrenamiento x y la salida deseada correspondiente y. Por lo general, lo entrenamos distribuyendo directamente x a través de la red, y luego propagándonos nuevamente para determinar la contribución del gradiente. Una excepción modifica este proceso. Comenzamos eliminando aleatoria y temporalmente la mitad de las neuronas ocultas en la red, dejando las neuronas de entrada y salida sin cambios. Después de eso, tendremos aproximadamente dicha red. Tenga en cuenta que las neuronas excluidas, aquellas que se eliminan temporalmente, todavía están marcadas en el diagrama:
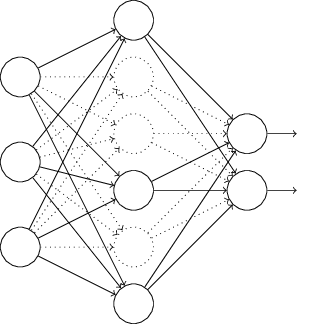
Pasamos x por distribución directa a través de la red modificada, y luego distribuimos de nuevo el resultado, también a través de la red modificada. Después de hacer esto con un mini paquete de ejemplos, actualizamos los pesos y compensaciones correspondientes. Luego, repetimos este proceso, primero restaurando las neuronas excluidas, luego eligiendo un nuevo subconjunto aleatorio de neuronas ocultas para eliminar, evaluar el gradiente para otro mini paquete y actualizar los pesos y las compensaciones de la red.
Repitiendo este proceso una y otra vez, obtenemos una red que ha aprendido algunos pesos y desplazamientos. Naturalmente, estos pesos y desplazamientos se aprendieron en condiciones en las que se excluyó la mitad de las neuronas ocultas.
Y cuando lancemos la red en su totalidad, tendremos el doble de neuronas ocultas activas. Para compensar esto, reducimos a la mitad los pesos que provienen de las neuronas ocultas.El procedimiento de exclusión puede parecer extraño y arbitrario. ¿Por qué debería ayudarla con la regularización? Para explicar lo que está sucediendo, quiero que se olviden de la excepción por un tiempo y presenten la capacitación de la Asamblea Nacional de manera estándar. En particular, imagine que entrenamos varios NS diferentes utilizando los mismos datos de entrenamiento. Por supuesto, las redes pueden variar al principio y, a veces, la capacitación puede producir resultados diferentes. En tales casos, podríamos aplicar algún tipo de promedio o esquema de votación para decidir qué resultados aceptar. Por ejemplo, si capacitamos a cinco redes, y tres de ellas clasifican el número como "3", entonces este es probablemente el verdadero tres. Y las otras dos redes probablemente estén equivocadas. Tal esquema de promedios es a menudo una forma útil (aunque costosa) de reducir el reciclaje. El motivo esque diferentes redes pueden volver a capacitarse de diferentes maneras, y el promedio puede ayudar a eliminar dicha reentrenamiento.¿Cómo se relaciona todo esto con la excepción? Heurísticamente, cuando excluimos diferentes conjuntos de neutrones, es como si estuviéramos entrenando diferentes NS. Por lo tanto, el procedimiento de exclusión es similar a los efectos promedio en una gran cantidad de redes diferentes. Las diferentes redes se vuelven a entrenar de diferentes maneras, por lo que se espera que el efecto promedio de la exclusión reduzca la reentrenamiento.Una explicación heurística relacionada de los beneficios de la exclusión se da en uno de los primeros trabajos.usando esta técnica: “Esta técnica reduce la compleja adaptación articular de las neuronas, porque la neurona no puede confiar en la presencia de ciertos vecinos. Al final, tiene que aprender rasgos más confiables que pueden ser útiles para trabajar junto con muchos subconjuntos aleatorios diferentes de neuronas ". En otras palabras, si imaginamos a nuestra Asamblea Nacional como un modelo que hace predicciones, entonces una excepción será una forma de garantizar la estabilidad del modelo ante la pérdida de partes individuales de evidencia. En este sentido, la técnica se asemeja a las regularizaciones de L1 y L2, que buscan reducir los pesos, y de esta manera hacen que la red sea más resistente a la pérdida de cualquier conexión individual en la red.Naturalmente, la verdadera medida de la utilidad de la exclusión es su tremendo éxito en mejorar la eficiencia de las redes neuronales. En la obra originaldonde se introdujo este método, se aplicó a muchas tareas diferentes. Estamos particularmente interesados en el hecho de que los autores aplicaron la excepción a la clasificación de números de MNIST, usando una red de distribución directa simple similar a la que examinamos. El documento señala que hasta entonces, el mejor resultado para dicha arquitectura era el 98.4% de precisión. Lo mejoraron al 98.7% usando una combinación de exclusión y una forma modificada de regularización L2. Se obtuvieron resultados igualmente impresionantes para muchas otras tareas, incluido el reconocimiento de patrones y del habla, y el procesamiento del lenguaje natural. La excepción fue especialmente útil en el entrenamiento de grandes redes profundas, donde a menudo surge el problema del reciclaje.Conjunto de datos de entrenamiento que se expande artificialmente
Vimos anteriormente que nuestra precisión de clasificación MNIST cayó al 80 por ciento, cuando usamos solo 1,000 imágenes de entrenamiento. Y no es de extrañar: con menos datos, nuestra red encontrará menos opciones para escribir números por personas. Intentemos entrenar a nuestra red de 30 neuronas ocultas, utilizando diferentes volúmenes del conjunto de entrenamiento para observar el cambio en la eficiencia. Entrenamos usando el tamaño de mini-paquete de 10, la velocidad de aprendizaje η = 0.5, el parámetro de regularización λ = 5.0 y la función de costo con entropía cruzada. Entrenaremos una red de 30 eras utilizando un conjunto completo de datos y aumentaremos el número de eras en proporción a la disminución en el volumen de datos de entrenamiento. Para garantizar el mismo factor de reducción de peso para diferentes conjuntos de datos de entrenamiento, utilizaremos el parámetro de regularización λ = 5,0 con un conjunto de entrenamiento completo y reduzca proporcionalmente con una disminución en los volúmenes de datos.
Ejercicio
- Como discutimos anteriormente, una forma de extender los datos de entrenamiento de MNIST es usar pequeñas rotaciones de las imágenes de entrenamiento. ¿Qué problema puede aparecer si permitimos la rotación de las imágenes en cualquier ángulo?
Digresión de grandes datos y el significado de comparar la precisión de la clasificación
Echemos un vistazo nuevamente a cómo la precisión de nuestro NS varía según el tamaño del conjunto de entrenamiento:Suponga que, en lugar de utilizar NS, usaríamos otra tecnología de aprendizaje automático para clasificar los números. Por ejemplo, intentemos usar el método de máquina de vectores de soporte (SVM), que conocimos brevemente en el Capítulo 1. Como entonces, no se preocupe si no está familiarizado con SVM, no necesitamos comprender sus detalles. Usaremos SVM a través de la biblioteca scikit-learn. Así es como la efectividad de SVM varía con el tamaño del conjunto de entrenamiento. A modo de comparación, puse el calendario y los resultados de la Asamblea Nacional.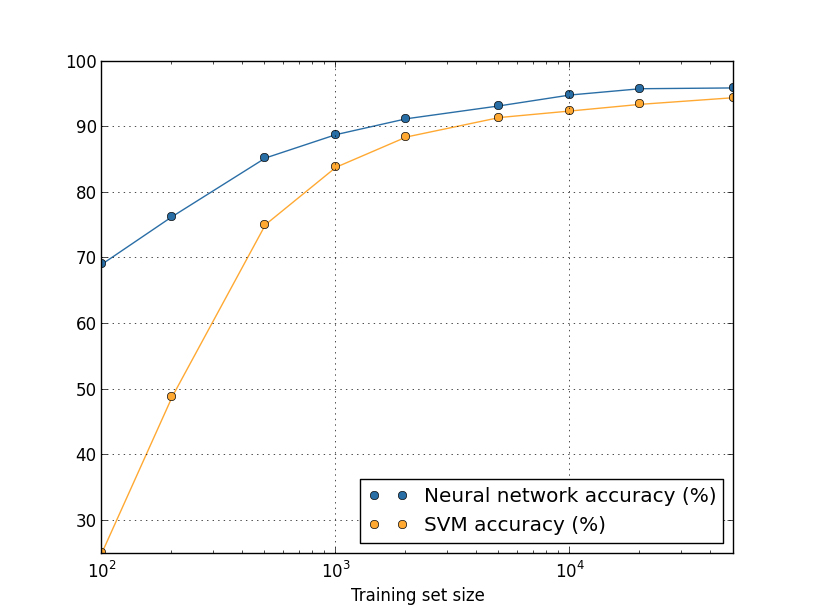
Desafío
- . ? . – , , , . , . - ? , .
Resumen
Hemos completado nuestra inmersión en el reciclaje y la regularización. Por supuesto, volveremos a estos problemas. Como ya he mencionado varias veces, la recapacitación es un gran problema en el campo de NS, especialmente a medida que las computadoras se vuelven más potentes y podemos entrenar redes más grandes. Como resultado, existe una necesidad urgente de desarrollar técnicas efectivas de regularización para reducir el reciclaje, por lo que esta área es muy activa hoy.
Inicialización de peso
Cuando creamos nuestro NS, debemos elegir los valores iniciales de los pesos y las compensaciones. Hasta ahora, los hemos elegido de acuerdo con las pautas brevemente descritas en el Capítulo 1. Permítanme recordarles que elegimos pesos y compensaciones basados en una distribución gaussiana independiente con una expectativa matemática de 0 y una desviación estándar de 1. Este enfoque funcionó bien, pero parece bastante arbitrario, por lo que vale la pena. revíselo y piense si es posible encontrar una mejor manera de asignar los pesos y desplazamientos iniciales y, tal vez, ayudar a nuestros NS a aprender más rápido.
Resulta que el proceso de inicialización se puede mejorar seriamente en comparación con la distribución gaussiana normalizada. Para entender esto, digamos que trabajamos con una red con una gran cantidad de neuronas de entrada, digamos, desde 1000. Y digamos que usamos la distribución Gaussiana normalizada para inicializar los pesos conectados a la primera capa oculta. Hasta ahora, me enfocaré solo en las escalas que conectan las neuronas de entrada a la primera neurona en la capa oculta, e ignoraré el resto de la red:
Para simplificar, imaginemos que estamos tratando de entrenar la red con la entrada x, en la que la mitad de las neuronas de entrada están activadas, es decir, tienen un valor de 1 y la otra mitad están desactivadas, es decir, tienen un valor de 0. El siguiente argumento funciona en un caso más general, pero es más fácil para usted lo entenderé en este ejemplo particular. Considere la suma ponderada z = ∑
j w
j x
j + b de entradas para una neurona oculta. Los 500 miembros de la suma desaparecen porque la x
j correspondiente es 0. Por lo tanto, z es la suma de 501 variables aleatorias gaussianas normalizadas, 500 pesos y 1 desplazamiento adicional. Por lo tanto, el valor z en sí tiene una distribución gaussiana con una expectativa matemática de 0 y una desviación estándar de √501 ≈ 22.4. Es decir, z tiene una distribución gaussiana bastante amplia, sin picos agudos:

En particular, este gráfico muestra que | z | es probable que sea bastante grande, es decir, z ≫ 1 o z ≫ -1. En este caso, la salida de las neuronas ocultas σ (z) estará muy cerca de 1 o 0. Esto significa que nuestra neurona oculta estará saturada. Y cuando esto sucede, como ya sabemos, pequeños cambios en los pesos producirán pequeños cambios en la activación de una neurona oculta. Estos pequeños cambios, a su vez, prácticamente no afectarán a los neutrones restantes en la red, y veremos los pequeños cambios correspondientes en la función de costo. Como resultado, estos pesos se entrenarán muy lentamente cuando usemos el algoritmo de descenso de gradiente. Esto es similar a la tarea que ya discutimos en este capítulo, en la que las neuronas de salida saturadas con valores incorrectos hacen que el aprendizaje se ralentice. Solíamos resolver este problema eligiendo inteligentemente una función de costo. Desafortunadamente, aunque esto ayudó con las neuronas de salida saturadas, no ayuda en absoluto con la saturación de las neuronas ocultas.
Ahora hablé sobre las escalas entrantes de la primera capa oculta. Naturalmente, los mismos argumentos se aplican a las siguientes capas ocultas: si los pesos en las capas ocultas posteriores se inicializan utilizando distribuciones gaussianas normalizadas, su activación a menudo será cercana a 0 o 1, y el entrenamiento irá muy lentamente.
¿Hay alguna manera de elegir las mejores opciones de inicialización para pesos y compensaciones, para que no tengamos tanta saturación y podamos evitar retrasos en el aprendizaje? Supongamos que tenemos una neurona con el número de pesos entrantes n
en . Luego, necesitamos inicializar estos pesos con distribuciones gaussianas aleatorias con una expectativa matemática de 0 y una desviación estándar de 1 / √n
en . Es decir, comprimimos los gaussianos y reducimos la probabilidad de saturación de la neurona. Luego, elegimos una distribución gaussiana para desplazamientos con una expectativa matemática de 0 y una desviación estándar de 1, por razones a las que volveré más adelante. Una vez hecha esta elección, nuevamente encontramos que z = ∑
j w
j x
j + b será una variable aleatoria con una distribución gaussiana con una expectativa matemática de 0, pero con un pico mucho más pronunciado que antes. Suponga, como antes, que 500 entradas son 0 y 500 son 1. Entonces es fácil mostrar (vea el ejercicio a continuación) que z tiene una distribución gaussiana con una expectativa matemática de 0 y una desviación estándar de √ (3/2) = 1.22 ... Este gráfico tiene un pico mucho más nítido, tanto que incluso en la imagen a continuación la situación está algo subestimada, porque tuve que cambiar la escala del eje vertical en comparación con el gráfico anterior:
Tal neurona estará saturada con una probabilidad mucho más baja y, en consecuencia, con una probabilidad más baja encontrará una desaceleración en el aprendizaje.
Ejercicio
- Confirme que la desviación estándar de z = ∑ j w j x j + b del párrafo anterior es √ (3/2). Consideraciones a favor de esto: la varianza de la suma de las variables aleatorias independientes es igual a la suma de las varianzas de las variables aleatorias individuales; la varianza es igual al cuadrado de la desviación estándar.
Mencioné anteriormente que continuaremos inicializando los desplazamientos, como antes, basados en una distribución gaussiana independiente con una expectativa matemática de 0 y una desviación estándar de 1. Y esto es normal, porque no aumenta en gran medida la probabilidad de saturación de nuestras neuronas. En realidad, la inicialización de las compensaciones no importa mucho si logramos evitar el problema de saturación. Algunos incluso intentan inicializar todas las compensaciones a cero, y confían en el hecho de que el descenso de gradiente puede aprender las compensaciones apropiadas. Pero dado que la probabilidad de que esto afecte algo es pequeña, continuaremos usando el mismo procedimiento de inicialización que antes.
Comparemos los resultados de los enfoques antiguos y nuevos para inicializar pesos utilizando la tarea de clasificar números de MNIST. Como antes, utilizaremos 30 neuronas ocultas, un mini paquete de tamaño 10, un parámetro de regularización & lambda = 5.0 y una función de costo con entropía cruzada. Reduciremos gradualmente la velocidad de aprendizaje de η = 0.5 a 0.1, ya que de esta forma los resultados serán ligeramente mejores visibles en los gráficos. Puede aprender usando el antiguo método de inicialización de peso:
>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True)
También puede aprender usando el nuevo enfoque para inicializar pesos. Esto es aún más simple, porque por defecto network2 inicializa los pesos usando un nuevo enfoque. Esto significa que podemos omitir la llamada net.large_weight_initializer () anterior:
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True)
Trazamos (usando el programa weight_initialization.py):
En ambos casos, se obtiene una precisión de clasificación del 96%. La precisión resultante es casi la misma en ambos casos. Pero la nueva técnica de inicialización llega a este punto mucho, mucho más rápido. Al final de la última era de entrenamiento, el antiguo enfoque para inicializar pesos alcanza una precisión del 87%, y el nuevo enfoque ya se acerca al 93%. Aparentemente, un nuevo enfoque para inicializar pesos comienza desde una posición mucho mejor, por lo que obtenemos buenos resultados mucho más rápido. El mismo fenómeno se observa si construimos los resultados para una red con 100 neuronas:
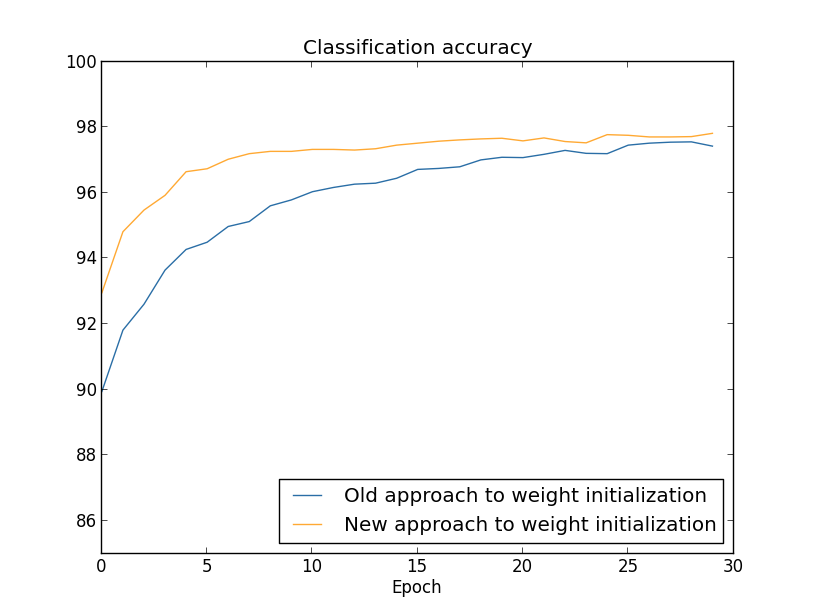
En este caso, no se producen dos curvas. Sin embargo, mis experimentos dicen que si agrega un poco más de eras, entonces la precisión comienza a coincidir. Por lo tanto, sobre la base de estos experimentos, podemos decir que mejorar la inicialización de los pesos solo acelera el entrenamiento, pero no cambia la eficiencia general de la red. Sin embargo, en el capítulo 4 veremos ejemplos de NS en los que la eficiencia a largo plazo mejora significativamente como resultado de la inicialización de los pesos a través de 1 / √n. Por lo tanto, mejora no solo la velocidad de aprendizaje, sino a veces la efectividad resultante.
El enfoque para inicializar pesos a través de 1 / √n ayuda a mejorar el entrenamiento de las redes neuronales. Se han propuesto otras técnicas para inicializar pesos, muchas de las cuales se basan en esta idea básica. No los consideraré aquí, ya que 1 / √n funciona bien para nuestros propósitos. Si está interesado, le recomiendo leer la discusión en las páginas 14 y 15 en un
documento de 2012 de Yoshua Benggio.
Desafío
- La combinación de regularización y un método mejorado de inicialización de peso. A veces, la regularización de L2 automáticamente nos da resultados similares a un nuevo método de inicialización de pesos. Digamos que usamos el viejo enfoque para inicializar pesos. Resuma un argumento heurístico que demuestre que: (1) si λ no es demasiado pequeño, entonces, en las primeras épocas de entrenamiento, el debilitamiento de los pesos dominará casi por completo; (2) si ηλ ≪ n, entonces los pesos se debilitarán e −ηλ / m veces en la época; (3) si λ no es demasiado grande, el debilitamiento de los pesos se ralentizará cuando los pesos disminuyan a aproximadamente 1 / √n, donde n es el número total de pesos en la red. Demuestre que estas condiciones se cumplen en los ejemplos para los que se construyen gráficos en esta sección.
Volviendo al reconocimiento de escritura a mano: código
Pongamos en práctica las ideas descritas en este capítulo. Desarrollaremos un nuevo programa, network2.py, una versión mejorada del programa network.py que creamos en el capítulo 1. Si no ha visto su código durante mucho tiempo, es posible que deba revisarlo rápidamente. Estas son solo 74 líneas de código, y es fácil de entender.
Al igual que con network.py, la estrella de network2.py es la clase Network, que usamos para representar nuestros NS. Inicializamos la instancia de clase con una lista de tamaños de las capas de red correspondientes, y con la elección de la función de costo, por defecto será entropía cruzada:
class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost
Las primeras dos líneas del método __init__ son las mismas que network.py, y se entienden por sí mismas. Las siguientes dos líneas son nuevas y debemos comprender en detalle lo que están haciendo.
Comencemos con el método default_weight_initializer. Utiliza un enfoque nuevo y mejorado para inicializar pesas. Como hemos visto, en este enfoque, los pesos que ingresan a la neurona se inicializan sobre la base de una distribución gaussiana independiente con una expectativa matemática de 0 y una desviación estándar de 1 dividida por la raíz cuadrada del número de enlaces entrantes a la neurona. Además, este método inicializará los desplazamientos utilizando la distribución gaussiana con una media de 0 y una desviación estándar de 1. Aquí está el código:
def default_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]
Para entenderlo, debe recordar que np es una biblioteca de Numpy que se ocupa del álgebra lineal. Lo importamos al comienzo del programa. También tenga en cuenta que no inicializamos desplazamientos en la primera capa de neuronas. La primera capa es entrante, por lo que no se utilizan desplazamientos. Lo mismo fue network.py.
Además del método default_weight_initializer, crearemos un método large_weight_initializer. Inicializa los pesos y las compensaciones utilizando el enfoque anterior del Capítulo 1, donde los pesos y las compensaciones se inicializan en función de una distribución gaussiana independiente con una expectativa matemática de 0 y una desviación estándar de 1. Este código, por supuesto, no es muy diferente de default_weight_initializer:
def large_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]
Incluí este método principalmente porque era más conveniente para nosotros comparar los resultados de este capítulo y el capítulo 1. ¡No puedo imaginar ninguna opción real en la que recomendaría usarlo!
La segunda novedad del método __init__ será la inicialización del atributo de costo. Para comprender cómo funciona esto, veamos la clase que usamos para representar la función de costo de entropía cruzada (la directiva @staticmethod le dice al intérprete que este método es independiente del objeto, por lo que el parámetro self no se pasa a los métodos fn y delta).
class CrossEntropyCost(object): @staticmethod def fn(a, y): return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): return (ay)
Vamos a resolverlo. Lo primero que se puede ver aquí es que, aunque la entropía cruzada es una función desde un punto de vista matemático, la implementamos como una clase de python, no como una función de python. ¿Por qué decidí hacer esto? En nuestra red, el valor juega dos roles diferentes. Obvio: es una medida de qué tan bien la activación de salida a corresponde a la salida deseada y. Este rol lo proporciona el método CrossEntropyCost.fn. (Por cierto, tenga en cuenta que llamar a np.nan_to_num dentro de CrossEntropyCost.fn asegura que Numpy procese correctamente el logaritmo de los números cercanos a cero). Sin embargo, la función de costo se utiliza en nuestra red de la segunda manera. Recordamos del Capítulo 2 que al iniciar el algoritmo de retropropagación, debemos considerar el error de salida de la red δ
L. La forma del error de salida depende de la función de costo: diferentes funciones de costo tendrán diferentes formas de error de salida. Para la entropía cruzada, el error de salida, como sigue de la ecuación (66), será igual a:
Por lo tanto, defino un segundo método, CrossEntropyCost.delta, cuyo objetivo es explicar a la red cómo calcular el error de salida. Y luego combinamos estos dos métodos en una clase que contiene todo lo que nuestra red necesita saber sobre la función de costos.
Por una razón similar, network2.py contiene una clase que representa una función de costo cuadrático. Incluyendo esto para comparar con los resultados del Capítulo 1, ya que en el futuro utilizaremos principalmente la entropía cruzada. El código está abajo. El método QuadraticCost.fn es un cálculo simple del costo cuadrático asociado con la salida ay la salida deseada y. El valor devuelto por QuadraticCost.delta se basa en la expresión (30) para el error de salida del valor cuadrático, que derivamos en el Capítulo 2.
class QuadraticCost(object): @staticmethod def fn(a, y): return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): return (ay) * sigmoid_prime(z)
Ahora hemos descubierto las principales diferencias entre network2.py y network2.py. Todo es muy sencillo. Hay otros pequeños cambios que describiré a continuación, incluida la implementación de la regularización de L2. Antes de eso, veamos el código completo network2.py. No es necesario estudiarlo en detalle, pero vale la pena entender la estructura básica, en particular, leer los comentarios para comprender qué hace cada una de las partes del programa. ¡Por supuesto, no prohíbo profundizar en esta pregunta tanto como quieras! Si se pierde, intente leer el texto después del programa y vuelva al código nuevamente. En general, aquí está:
"""network2.py ~~~~~~~~~~~~~~ network.py, . – , , . , . , . """
Entre los cambios más interesantes está la inclusión de la regularización L2. Aunque este es un gran cambio conceptual, es tan fácil de implementar que es posible que no lo note en el código. En su mayor parte, esto es simplemente pasar el parámetro lmbda a diferentes métodos, especialmente Network.SGD. Todo el trabajo se lleva a cabo en una línea del programa, la cuarta desde el final en el método Network.update_mini_batch. Allí cambiamos la regla de actualización de descenso de gradiente para incluir la reducción de peso. ¡El cambio es pequeño, pero afecta gravemente los resultados!
Esto, por cierto, a menudo sucede cuando se implementan nuevas técnicas en redes neuronales. Pasamos miles de palabras discutiendo la regularización. Conceptualmente, esto es algo bastante sutil y difícil de entender. Sin embargo, se puede agregar trivialmente al programa. Inesperadamente, se pueden implementar técnicas complejas con cambios menores en el código.
Otro cambio pequeño pero importante en el código es la adición de varios indicadores opcionales al método de descenso de gradiente estocástico Network.SGD.
Estas banderas hacen posible rastrear el costo y la precisión en training_data o Evaluation_data, que pueden transmitirse a Network.SGD. Anteriormente en el capítulo, a menudo usamos estas banderas, pero permítanme dar un ejemplo de su uso, solo como recordatorio: >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True)
Configuramos Evaluation_data a través de validation_data. Sin embargo, podríamos rastrear el rendimiento en test_data y cualquier otro conjunto de datos. También tenemos cuatro indicadores que especifican la necesidad de rastrear el costo y la precisión tanto en Evaluation_data como en Training_data. Estas banderas están configuradas en False de manera predeterminada, sin embargo, se incluyen aquí para rastrear la efectividad de la Red. Además, el método Network.SGD de network2.py devuelve una tupla de cuatro elementos que representa los resultados del seguimiento. Puedes usarlo así: >>> evaluation_cost, evaluation_accuracy, ... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True)
Entonces, por ejemplo, Evaluation_cost será una lista de 30 elementos que contienen el costo de los datos estimados al final de cada era. Dicha información es extremadamente útil para comprender el comportamiento de una red neuronal. Dicha información es extremadamente útil para comprender el comportamiento de la red. Por ejemplo, puede usarse para dibujar gráficos de aprendizaje en red a lo largo del tiempo. Así es como construí todos los gráficos de este capítulo. Sin embargo, si uno de los indicadores no está configurado, el elemento de tupla correspondiente será una lista vacía.Otras adiciones de código incluyen el método Network.save, que guarda el objeto de red en el disco, y la función de cargarlo en la memoria. El guardado y la carga se realizan a través de JSON, no los módulos Python pickle o cPickle, que generalmente se usan para guardar en el disco y cargar en python. El uso de JSON requiere más código del que sería necesario para pickle o cPickle. Para entender por qué elegí JSON, imagine que en algún momento en el futuro decidimos cambiar nuestra clase de red para que haya más neuronas sigmoideas. Para implementar este cambio, lo más probable es que cambiemos los atributos definidos en el método Network .__ init__. Y si solo usáramos pickle para guardar, nuestra función de carga no funcionaría. El uso de JSON con serialización explícita nos facilita garantizarque las versiones anteriores del objeto de red se pueden descargar.Hay muchos pequeños cambios en el código, pero estas son solo pequeñas variaciones de network.py. El resultado final es una extensión de nuestro programa de 74 líneas a un programa mucho más funcional de 152 líneas.Desafío
- Modifique el siguiente código introduciendo la regularización L1, y utilícela para clasificar los dígitos MNIST por una red con 30 neuronas ocultas. ¿Puede elegir un parámetro de regularización que le permita mejorar el resultado en comparación con una red sin regularización?
- Network.cost_derivative method network.py. . ? , ? network2.py Network.cost_derivative, CrossEntropyCost.delta. ?