Hoy veremos un paquete gráfico para el lenguaje Julia llamado Luxor . Esta es una de esas herramientas que convierten el proceso de creación de imágenes vectoriales en la resolución de problemas lógicos con una tormenta de emociones.
Precaución Debajo del corte, 8,5 MB de imágenes livianas y gifs que representan huevos psicodélicos y objetos cuatridimensionales, ¡verlos puede causar una ligera nubosidad en la mente!
Instalación
https://julialang.org : descargue la distribución de Julia del sitio oficial. Luego, comenzando el intérprete, llevamos los comandos a su consola:
using Pkg Pkg.add("Colors") Pkg.add("ColorSchemes") Pkg.add("Luxor")
que instalará paquetes para trabajos avanzados con colores y el propio Luxor.
Posibles problemas
El principal problema de la programación moderna en general y del código abierto en particular es que algunos proyectos se construyen sobre otros, heredan todos los errores o incluso generan otros nuevos debido a incompatibilidades. Al igual que muchos otros paquetes, Luxor utiliza otros paquetes de julia para su trabajo, que, a su vez, son cáscaras de soluciones existentes.
Entonces, ImageMagick.jl no quería descargar ni guardar archivos. La solución se encontró en la página original : resultó que a él no le gusta el alfabeto cirílico de alguna manera.
El problema número dos surgió con el paquete de gráficos de bajo nivel Cairo en Windows 7. Ocultaré la solución aquí:
Bailando con una pandereta- Escribimos el intérprete
]add Gtk : el paquete para trabajar con gui comenzará a instalarse y lo más probable es que se caiga durante la construcción - A continuación, descargue gtk + -bundle_3.6.4-20130513_win64
- Durante la instalación, todo era necesario en la carpeta con los paquetes de Julia, pero gtk no se terminó durante la ejecución del elemento, por lo que descargamos la versión final para nuestra máquina; arrojamos el contenido del archivo descargado en el directorio C: \ Users \ User.julia \ packages \ WinRPM \ Y9QdZ \ deps \ usr \ x86_64-w64-mingw32 \ sys-root \ mingw (su ruta puede variar)
- Ejecute julia y conduzca
]build Gtk y después de construir using Gtk y, en aras de la fidelidad, reconstruya Luxor: ]build Luxor - Reiniciamos julia, y podemos usar de forma segura todo lo que necesitamos:
using Luxor
En caso de otros problemas, tratamos de encontrar nuestro caso.
Si quieres probar la animación
El paquete Luxor crea animaciones usando ffmpeg , siempre que esté presente en su computadora. ffmpeg es una biblioteca multiplataforma de código abierto para procesar archivos de video y audio, algo muy útil (hay una buena excursión en el concentrador ). Instalarlo:
- Descargar ffmpeg fuera del sitio. En mi caso, esta es una descarga para Windows
- Desempaquete y escriba la ruta a ffmpeg.exe en la variable Ruta .
Más acerca de la obstrucción en Path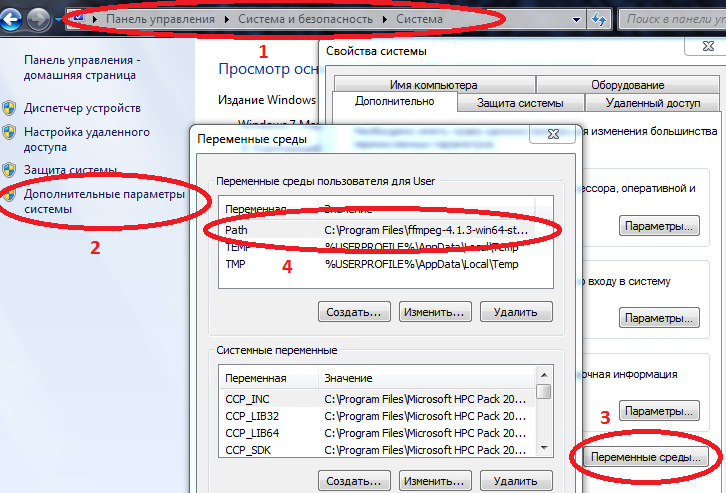
Computadora / Propiedades del sistema / Parámetros avanzados del sistema / Variables de entorno / Ruta (Crear si no) y agregue la ruta a su ffmpeg.exe allí
Ejemplo C: \ Archivos de programa \ ffmpeg-4.1.3-win64-static \ bin
si Path ya tiene valores, sepárelos con un punto y coma.
Ahora, si conduce ffmpeg con los parámetros necesarios en la consola de comandos ( cmd ), se iniciará y funcionará, y Julia solo se comunicará con él.
Hola mundo
Comencemos con un pequeño inconveniente: al crear una imagen, se crea un archivo gráfico y se guarda en el directorio de trabajo. Es decir, cuando trabaje en REPL, la carpeta raíz de Julia se obstruirá con imágenes, y si dibuja en Jupyter, las imágenes se acumularán junto al cuaderno del proyecto, por lo tanto, será un buen hábito establecer el directorio de trabajo en un lugar separado antes de comenzar a trabajar:
using Luxor cd("C:\\Users\\User\\Desktop\\mycop")
Crea el primer dibujo
Drawing(220, 220, "hw.png") origin() background("white") sethue("black") text("Hello world") circle(Point(0, 0), 100, :stroke) finish() preview()

Drawing() crea un dibujo, de forma predeterminada en formato PNG, el nombre de archivo predeterminado es 'luxor-drawing.png', el tamaño predeterminado es 800x800, para todos los formatos, excepto PNG, puede especificar tamaños no enteros y también puede usar tamaños de papel ("A0 "," A1 "," A2 "," A3 "," A4 "...)
finish() : finaliza el dibujo y cierra el archivo. Puede abrirlo en una aplicación de visualización externa usando preview() , que cuando trabaje en Jupyter (IJulia) mostrará un archivo PNG o SVG en el bloc de notas. Cuando trabaje en Juno, mostrará un archivo PNG o SVG en el panel Gráfico. En Repl, se llama a la herramienta para trabajar con imágenes que establezca para este formato en su sistema operativo.
Lo mismo se puede escribir en forma corta usando macros
@png begin text("Hello world") circle(Point(0, 0), 100, :stroke) end
Para formatos vectoriales EPS, SVG, PDF, todo funciona de la misma manera.
Huevo euclidiano

Esta es una forma bastante interesante de dibujar un huevo, y si conecta los puntos clave y corta a lo largo de las líneas recibidas, saldrá un tangram excelente
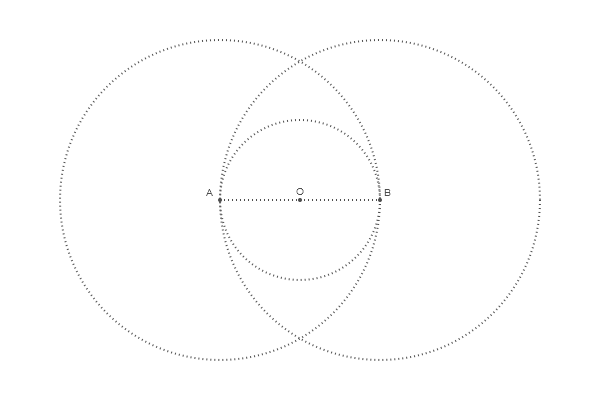
Comencemos con el círculo:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) end 200 200 "egg0"

Todo es extremadamente simple: setdash("dot") - dibuja con puntos, sethue("gray30") - color de línea: cuanto más pequeño, más oscuro, más cercano a 100 más blanco. La clase de punto se define sin nosotros, y el centro de coordenadas (0,0) se puede especificar con la letra O Agregue dos círculos y firme los puntos:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke) end 600 400 "egg2"
Para buscar puntos de intersección, hay una función llamada intersectionlinecircle() que encuentra el punto o puntos donde la línea se cruza con el círculo. Por lo tanto, podemos encontrar dos puntos donde uno de los círculos se cruza con una línea vertical imaginaria dibujada a través de O. Debido a la simetría, podemos procesar solo el círculo A.
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
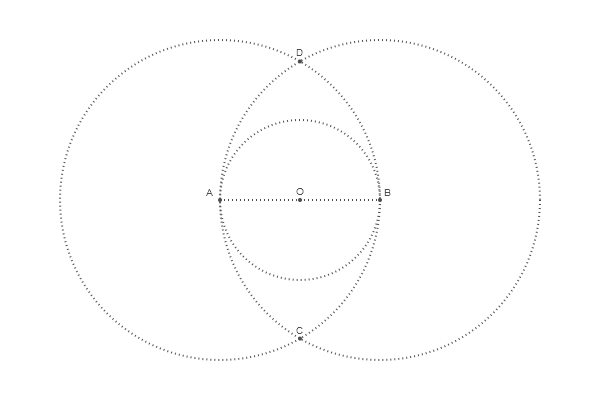
Para determinar el centro del círculo superior, encontramos la intersección OD
Código @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

El radio del círculo subordinado está determinado por la restricción a dos círculos grandes:
Código @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

El huevo esta listo! Queda por ensamblarlo a partir de cuatro arcos especificados por la función arc2r() y completar el área:
Código @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
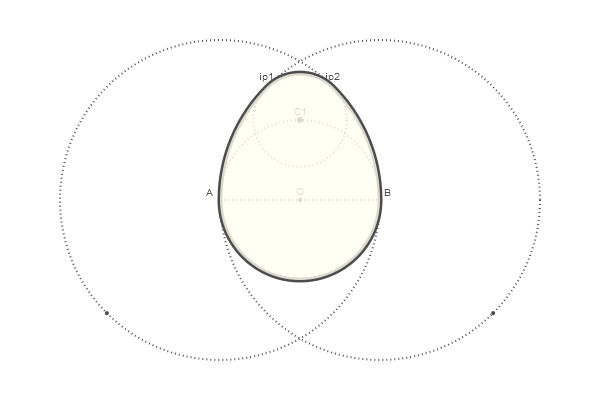
Y ahora, para disfrutar adecuadamente, llevaremos nuestros logros a
la función function egg(radius, action=:none) A, B = [Point(x, 0) for x in [-radius, radius]] nints, C, D = intersectionlinecircle(Point(0, -2radius), Point(0, 2radius), A, 2radius) flag, C1 = intersectionlinecircle(C, D, O, radius) nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius) nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius) if distance(C1, I1) < distance(C1, I2) ip1 = I1 else ip1 = I2 end if distance(C1, I3) < distance(C1, I4) ip2 = I3 else ip2 = I4 end newpath() arc2r(B, A, ip1, :path) arc2r(C1, ip1, ip2, :path) arc2r(A, ip2, B, :path) arc2r(O, B, A, :path) closepath() do_action(action) end
Utilizamos colores aleatorios, pintura de capas y varias condiciones iniciales:
@png begin setopacity(0.7) for θ in range(0, step=π/6, length=12) @layer begin rotate(θ) translate(100, 50)


Además del trazo y el relleno, puede usar el contorno como un área de recorte (recortar otra imagen en forma de huevo) o como base para varios diseñadores. La función egg () crea un esquema y le permite aplicarle una acción. También es posible transformar nuestra creación en un polígono (una matriz de puntos). El siguiente código convierte el contorno de un huevo en un polígono, y luego mueve cada punto del polígono hasta la mitad del centroide.
@png begin egg(160, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) circle(pc, 5, :fill) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.5) end poly(pgon, :stroke) end 350 500 "polyegg"

La apariencia desigual de los puntos internos aquí surge como resultado de la configuración de conexión de línea predeterminada. Experimente con setlinejoin("round") para ver si esto cambia la geometría. Bueno, ahora intentemos offsetpoly() creando un contorno poligonal fuera o dentro de un polígono existente.
@png begin egg(80, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.9) end for i in 30:-3:-8 randomhue() op = offsetpoly(pgon, i) poly(op, :stroke, close=true) end end 350 500 "polyeggs"

Pequeños cambios en la regularidad de los puntos creados al convertir la ruta en un polígono, y el número diferente de muestras que hizo, se amplifican constantemente en contornos sucesivos.
Animación
Primero, definamos las funciones que implementan el fondo y la representación del huevo, según el número de fotograma:
Código using Colors demo = Movie(400, 400, "test") function backdrop(scene, framenumber) background("black") end function frame(scene, framenumber) setopacity(0.7) θ = framenumber * π/6 @layer begin rotate(θ) translate(100, 50) egg(50, :path) setline(10) randomhue() fillpreserve() randomhue() strokepath() end end
La animación se implementa mediante un conjunto simple de comandos:
animate(demo, [ Scene(demo, backdrop, 0:12), Scene(demo, frame, 0:12, easingfunction=easeinoutcubic, optarg="made with Julia") ], framerate=10, tempdirectory="C:\\Users\\User\\Desktop\\mycop", creategif=true)
Lo que realmente causa nuestro ffmpeg
run(`ffmpeg -f image2 -i $(tempdirectory)/%10d.png -vf palettegen -y $(seq.stitle)-palette.png`) run(`ffmpeg -framerate 30 -f image2 -i $(tempdirectory)/%10d.png -i $(seq.stitle)-palette.png -lavfi paletteuse -y /tmp/$(seq.stitle).gif`)
Es decir, se crea una serie de imágenes y luego se ensambla un GIF a partir de estos marcos:

Pentahore
Es un núcleo de cinco núcleos , el simplex de cuatro dimensiones correcto. Para dibujar y manipular objetos de 4 dimensiones en imágenes de dos dimensiones, primero definimos
punto de 4 dimensiones de clase struct Point4D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 w::Float64 end Point4D(a::Array{Float64, 1}) = Point4D(a...) Base.size(pt::Point4D) = (4, ) Base.getindex(pt::Point4D, i) = [pt.x, pt.y, pt.z, pt.w][i] struct Point3D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 end Base.size(pt::Point3D) = (3, )
En lugar de definir muchas operaciones manualmente, podemos definir nuestra estructura como un subtipo de AbstractArray ( Más acerca de las clases como interfaces )
La tarea principal que debemos resolver es cómo convertir un punto 4D en un punto 2D. Comencemos con una tarea más simple: cómo convertir un punto 3D en un punto 2D, es decir ¿Cómo podemos dibujar una figura 3D en una superficie plana? Considera un cubo simple. Las superficies frontal y posterior pueden tener las mismas coordenadas X e Y y variar solo en sus valores Z.
Código @png begin fontface("Menlo") fontsize(8) setblend(blend( boxtopcenter(BoundingBox()), boxmiddlecenter(BoundingBox()), "skyblue", "white")) box(boxtopleft(BoundingBox()), boxmiddleright(BoundingBox()), :fill) setblend(blend( boxmiddlecenter(BoundingBox()), boxbottomcenter(BoundingBox()), "grey95", "grey45" )) box(boxmiddleleft(BoundingBox()), boxbottomright(BoundingBox()), :fill) sethue("black") setline(2) bx1 = box(O, 250, 250, vertices=true) poly(bx1, :stroke, close=true) label.(["-1 1 1", "-1 -1 1", "1 -1 1", "1 1 1"], slope.(O, bx1), bx1) setline(1) bx2 = box(O, 150, 150, vertices=true) poly(bx2, :stroke, close=true) label.(["-1 1 0", "-1 -1 0", "1 -1 0", "1 1 0"], slope.(O, bx2), bx2, offset=-45) map((x, y) -> line(x, y, :stroke), bx1, bx2) end 400 400 "cube.png"

Por lo tanto, la idea es proyectar un cubo de 3D a 2D, guardando los dos primeros valores y multiplicándolos o cambiándolos por el tercer valor. Cheque
como funciona const K = 4.0 function convert(Point, pt3::Point3D) k = 1/(K - pt3.z) return Point(pt3.x * k, pt3.y * k) end @png begin cube = Point3D[ Point3D(-1, -1, 1), Point3D(-1, 1, 1), Point3D( 1, -1, 1), Point3D( 1, 1, 1), Point3D(-1, -1, -1), Point3D(-1, 1, -1), Point3D( 1, -1, -1), Point3D( 1, 1, -1), ] circle.(convert.(Point, cube) * 300, 5, :fill) end 220 220 "points"

Usando el mismo principio, creemos un método para convertir puntos 4D y una función que tome una lista de puntos cuatridimensionales y los asigne dos veces a una lista de puntos bidimensionales adecuados para dibujar.
function convert(Point3D, pt4::Point4D) k = 1/(K - pt4.w) return Point3D(pt4.x * k, pt4.y * k, pt4.z * k) end function flatten(shape4) return map(pt3 -> convert(Point, pt3), map(pt4 -> convert(Point3D, pt4), shape4)) end
A continuación, configure los vértices y las caras y compruebe cómo funciona en color.
Tyk! const n = -1/√5 const pentachoron = [Point4D(vertex...) for vertex in [ [ 1.0, 1.0, 1.0, n], [ 1.0, -1.0, -1.0, n], [-1.0, 1.0, -1.0, n], [-1.0, -1.0, 1.0, n], [ 0.0, 0.0, 0.0, n + √5]]]; const pentachoronfaces = [ [1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]; @png begin setopacity(0.2) pentachoron2D = flatten(pentachoron) for (n, face) in enumerate(pentachoronfaces) randomhue() poly(1500 * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end 300 250 "5ceil"

Todos los desarrolladores de juegos respetuosos deben conocer los Fundamentos matemáticos de los gráficos de máquinas . Si nunca trató de comprimir, rotar, reflejar teteras en OpenGL , no se alarme, todo es bastante simple. Para reflejar un punto relativamente a una línea recta, o para rotar un plano alrededor de cierto eje, debe multiplicar las coordenadas por una matriz especial. En realidad, determinaremos las matrices de transformación que necesitamos:
recoger más function XY(θ) [cos(θ) -sin(θ) 0 0; sin(θ) cos(θ) 0 0; 0 0 1 0; 0 0 0 1] end function XW(θ) [cos(θ) 0 0 -sin(θ); 0 1 0 0; 0 0 1 0; sin(θ) 0 0 cos(θ)] end function XZ(θ) [cos(θ) 0 -sin(θ) 0; 0 1 0 0; sin(θ) 0 cos(θ) 0; 0 0 0 1] end function YZ(θ) [1 0 0 0; 0 cos(θ) -sin(θ) 0; 0 sin(θ) cos(θ) 0; 0 0 0 1] end function YW(θ) [1 0 0 0; 0 cos(θ) 0 -sin(θ); 0 0 1 0; 0 sin(θ) 0 cos(θ)] end function ZW(θ) [1 0 0 0; 0 1 0 0; 0 0 cos(θ) -sin(θ); 0 0 sin(θ) cos(θ)]; end function rotate4(A, matrixfunction) return map(A) do pt4 Point4D(matrixfunction * pt4) end end
Por lo general, gira puntos en un plano en relación con un objeto unidimensional. Los puntos 3D están alrededor de una línea 2D (a menudo este es uno de los ejes XYZ). Por lo tanto, es lógico que los puntos 4D roten en relación con el plano 3D. Hemos identificado matrices que realizan una rotación de cuatro dimensiones alrededor de un plano definido por dos ejes X, Y, Z y W. El plano XY suele ser el plano de la superficie de dibujo. Si percibe el plano XY como una pantalla de computadora, entonces el plano XZ es paralelo a su mesa o piso, y el plano YZ es la pared al lado de su mesa a la derecha o izquierda. Pero, ¿qué pasa con XW, YW y ZW? Este es el misterio de las figuras de cuatro dimensiones: no podemos ver estos planos, solo podemos imaginar su existencia al observar cómo las formas se mueven a través de ellos y alrededor de ellos.
Ahora establecemos las funciones para los cuadros y cosimos la animación:
spoiler using ColorSchemes function frame(scene, framenumber, scalefactor=1000) background("white")

Bueno, y otro ángulo:
Código function frame(scene, framenumber, scalefactor=1000) background("antiquewhite") setlinejoin("bevel") setline(1.0) setopacity(0.2) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) pentachoron2D = flatten( rotate4( pentachoron, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(pentachoronfaces) sethue(get(ColorSchemes.diverging_rainbow_bgymr_45_85_c67_n256, n/length(pentachoronfaces))) poly(scalefactor * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end makemovie(500, 500, "pentachoron-xz-yw.gif", scalefactor=2000)
El deseo de realizar un objeto cuatridimensional más popular, el Tesseract, se hace completamente
Tops y caras const tesseract = [Point4D(vertex...) for vertex in [ [-1, -1, -1, 1], [ 1, -1, -1, 1], [ 1, 1, -1, 1], [-1, 1, -1, 1], [-1, -1, 1, 1], [ 1, -1, 1, 1], [ 1, 1, 1, 1], [-1, 1, 1, 1], [-1, -1, -1, -1], [ 1, -1, -1, -1], [ 1, 1, -1, -1], [-1, 1, -1, -1], [-1, -1, 1, -1], [ 1, -1, 1, -1], [ 1, 1, 1, -1], [-1, 1, 1, -1]]] const tesseractfaces = [ [1, 2, 3, 4], [1, 2, 10, 9], [1, 4, 8, 5], [1, 5, 6, 2], [1, 9, 12, 4], [2, 3, 11, 10], [2, 3, 7, 6], [3, 4, 8, 7], [5, 6, 14, 13], [5, 6, 7, 8], [5, 8, 16, 13], [6, 7, 15, 14], [7, 8, 16, 15], [9, 10, 11, 12], [9, 10, 14, 13], [9, 13, 16, 12], [10, 11, 15, 14], [13, 14, 15, 16]];
Crear animación function frame(scene, framenumber, scalefactor=1000) background("black") setlinejoin("bevel") setline(10.0) setopacity(0.7) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) tesseract2D = flatten( rotate4( tesseract, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(tesseractfaces) sethue([Luxor.lighter_blue, Luxor.lighter_green, Luxor.lighter_purple, Luxor.lighter_red][mod1(n, 4)]...) poly(scalefactor * tesseract2D[face], :fillpreserve, close=true) sethue([Luxor.darker_blue, Luxor.darker_green, Luxor.darker_purple, Luxor.darker_red][mod1(n, 4)]...) strokepath() end end makemovie(500, 500, "tesseract-xz-yw.gif", scalefactor=1000)

Tarea: automatice la creación de matrices de coordenadas y números de vértices ( permutaciones con repeticiones y sin repeticiones, respectivamente ). Además, no utilizamos todas las matrices de traducción; Cada nueva perspectiva trae un nuevo "¡Guau!", Pero decidí no sobrecargar la página. Bueno, puedes experimentar con muchas caras y dimensiones.
Referencias