Eliminar el ruido de alta frecuencia de las señales de los sensores de vibración durante el diagnóstico de vibración de los rodamientos

Foto tomada de la publicación.

Introduccion

Una de las tareas más urgentes del procesamiento de la señal digital es la tarea de limpiar la señal del ruido. Cualquier señal práctica contiene no solo información útil, sino también rastros de algunos efectos extraños de interferencia o ruido. Además, durante el diagnóstico de vibración, las señales de los sensores de vibración tienen un espectro de frecuencia no estacionario, lo que complica la tarea de filtrado.

Hay muchas formas diferentes de eliminar el ruido de alta frecuencia de una señal. Por ejemplo, la biblioteca Scipy contiene filtros basados ​​en varios métodos de filtrado: Kalman; suavizando la señal promediando a lo largo del eje de tiempo y otros.

Sin embargo, la ventaja del método de transformación de wavelet discreta (DWT) es la variedad de formas de wavelet. Puede seleccionar una wavelet, que tendrá una forma característica de los fenómenos esperados. Por ejemplo, puede seleccionar una señal en un rango de frecuencia dado, cuya forma es responsable de la aparición de un defecto.

El propósito de esta publicación es analizar los métodos de filtrado de las señales de los sensores de vibración utilizando la conversión de señal DWT, el filtro de Kalman y el método de promedio móvil.

Fuente de datos para análisis

En la publicación, se analizará el funcionamiento de los filtros basados ​​en varios métodos de filtrado utilizando un conjunto de datos de la NASA . Datos obtenidos en la plataforma experimental PRONOSTIA:



El kit contiene datos sobre las señales del sensor de vibración para el desgaste de varios tipos de rodamientos. El propósito de las carpetas con los archivos de señal se da en la tabla :



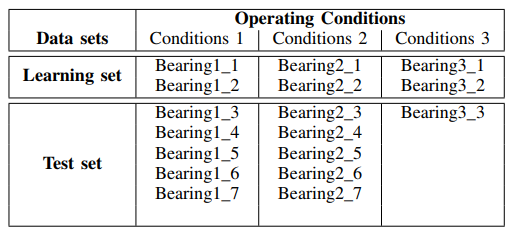
El monitoreo del estado de los rodamientos es proporcionado por las señales de los sensores de vibración (acelerómetros horizontales y verticales), la fuerza y ​​la temperatura.



Señales recibidas para tres cargas diferentes:

• Primeras condiciones de trabajo: 1800 rpm y 4000 N;
• Segundas condiciones de trabajo: 1650 rpm y 4200 N;
• Terceras condiciones de funcionamiento: 1500 rpm y 5000 N.

Para estas condiciones, utilizando la conversión continua de señal wavelet, construimos los escalogramas de espectro de potencia para los datos del conjunto de prueba: un archivo (para un tipo de rodamientos) de las carpetas: ['Test_set / Bearing1_3 / acc_00001.csv', 'Test_set / Bearing2_3 / acc_00001. csv ',' Test_set / Bearing3_3 / acc_00001.csv '] (ver tabla 1).






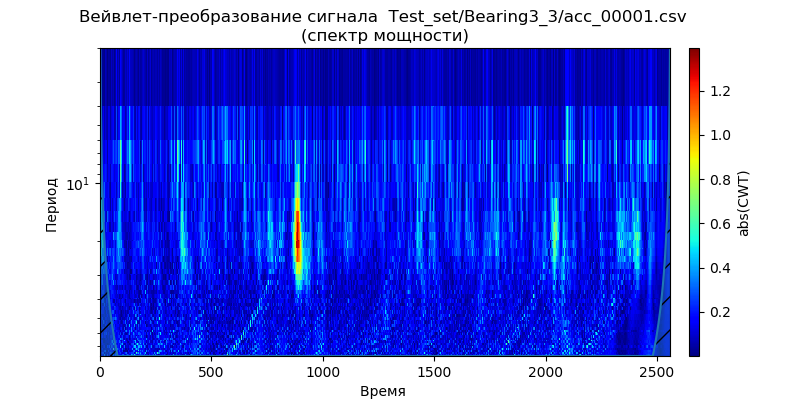
De los escaogramas dados se deduce que los momentos de aumento de la potencia del espectro aparecen antes en el tiempo y demuestran la frecuencia para las condiciones de operación: 1650 rpm y 4200 N, lo que indica una degradación acelerada de los rodamientos en esta banda de frecuencia para la fuerza reducida. Utilizaremos esta señal ('Test_set / Bearing2_3 / acc_00001.csv') para analizar los métodos de eliminación de ruido.

Deconstrucción de señal utilizando DWT

En la publicación, vimos cómo se implementa un banco de filtros en el DWT que puede deconstruir una señal en sus subbandas de frecuencia. Los coeficientes de aproximación (cA) representan la parte de baja frecuencia de la señal (filtro de promedio). Los coeficientes de detalle (cD) representan la porción de alta frecuencia de la señal. A continuación, examinaremos cómo se puede usar DWT para deconstruir una señal en sus subbandas de frecuencia y restaurar la señal original.

Hay dos formas de resolver el problema de deconstrucción de señal utilizando las herramientas PyWavelets:

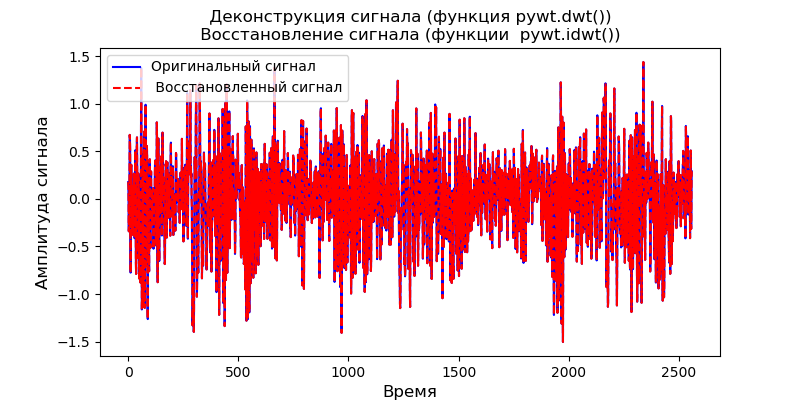
La primera forma es aplicar pywt.dwt () a la señal para extraer los coeficientes de aproximación y detalle (cA1, cD1). Luego, para restaurar la señal, usaremos pywt.idwt ():




La segunda forma de aplicar la función pywt.wavedec () a la señal es restaurar todos los coeficientes de aproximación y detalle a un cierto nivel. Esta función toma la señal y el nivel iniciales como entrada y devuelve un conjunto de coeficientes de aproximación (enésimo nivel) yn conjuntos de coeficientes de detalle (del 1 al enésimo nivel). Para la deconstrucción, aplique pywt.waverec ():



La segunda forma de deconstruir y restaurar la señal es más conveniente, ya que le permite establecer inmediatamente el nivel deseado de deconstrucción.

Eliminar el ruido de alta frecuencia eliminando algunos de los coeficientes de detalle durante la deconstrucción de la señal

Restauraremos la señal eliminando algunos de los coeficientes de detalle. Dado que los coeficientes de detalle representan la parte de alta frecuencia de la señal, simplemente filtramos esta parte del espectro de frecuencia. Si hay ruido de alta frecuencia en la señal, esta es una forma de filtrarlo.

En la biblioteca PyWavelets, esto se puede hacer usando la función de procesamiento de umbral pywt.threshol ():

pywt.threshold (datos, valor, modo = 'soft', sustituto = 0) ¶
data: array_like
Datos numéricos
valor: escalar
Valor umbral
modo: {'suave', 'duro', 'garrote', 'mayor', 'menor'}
Define el tipo de umbral que se aplicará a la entrada. El valor predeterminado es "suave".
sustituto: flotador, opcional
Valor de sustitución (predeterminado: 0).
salida: matriz
Arreglo de umbral.

La aplicación de la función de procesamiento de umbral para un valor de umbral dado se considera mejor usando el siguiente ejemplo:

 >>>> from scipy import* >>> import pywt >>> data =linspace(1, 4, 7) >>> data array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'soft') array([0. , 0. , 0. , 0.5, 1. , 1.5, 2. ]) >>> pywt.threshold(data, 2, 'hard') array([0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'garrote') array([0. , 0. , 0., 0.9,1.66666667, 2.35714286, 3.]) 

Trazamos el gráfico de la función de umbral usando la siguiente lista:



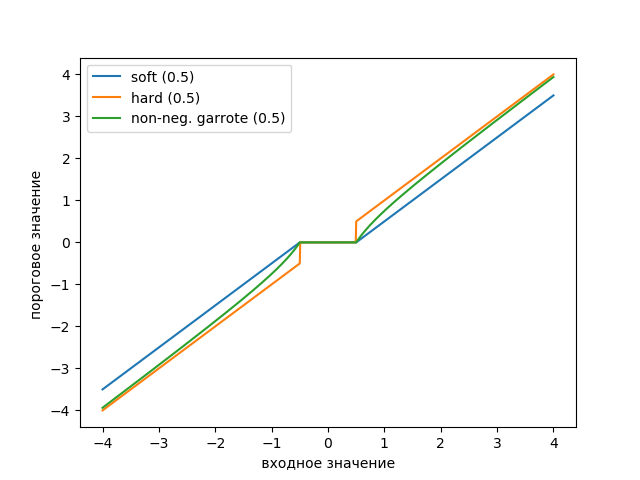
El gráfico muestra que el umbral de Garott no negativo es intermedio entre el umbral blando y el duro. Se requieren un par de umbrales que definen el ancho de la región de transición.

La influencia de la función umbral en las características del filtro

Como se deduce del gráfico anterior, solo dos funciones de umbral 'soft' y 'garrote' son adecuadas para nosotros, para estudiar su influencia en las características del filtro, anotamos la lista:





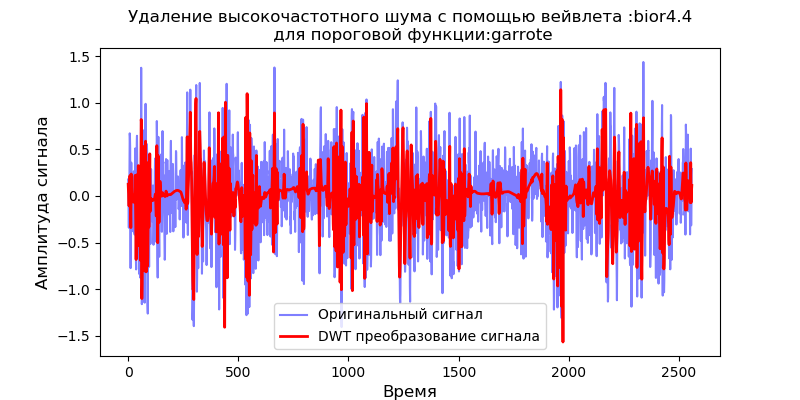
Como se desprende de los gráficos, la función suave proporciona un mejor suavizado que la función 'garrote', por lo que utilizaremos la función suave en el futuro.

La influencia del umbral de detalle en las características del filtro.

Para el tipo de filtro en consideración, el umbral para cambiar los coeficientes de detalle es una característica importante, por lo tanto, estudiamos su efecto utilizando la siguiente lista:






Como se deduce de los gráficos obtenidos, el umbral del nivel de detalle afecta la escala de las partes apantalladas. Con un aumento en el umbral, la wavelet resta ruido de un nivel cada vez mayor hasta que se produce un aumento excesivo de la escala de detalle y la transformación comienza a distorsionar la forma de la señal original. Para nuestra señal, el umbral no debe ser superior a 0,63.

El efecto de wavelet en las características del filtro

La biblioteca PyWavelets tiene un número suficiente de wavelets para la conversión DWT, que se puede obtener de esta manera:

 >>> import pywt >>> print(pywt.wavelist(kind= 'discrete')) ['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20'] 

La influencia de la wavelet en la característica del filtro depende de su función primitiva. Para demostrar esta dependencia, seleccionamos dos wavelets de la familia Dobeshi: db1 y db38, y consideramos estas familias:




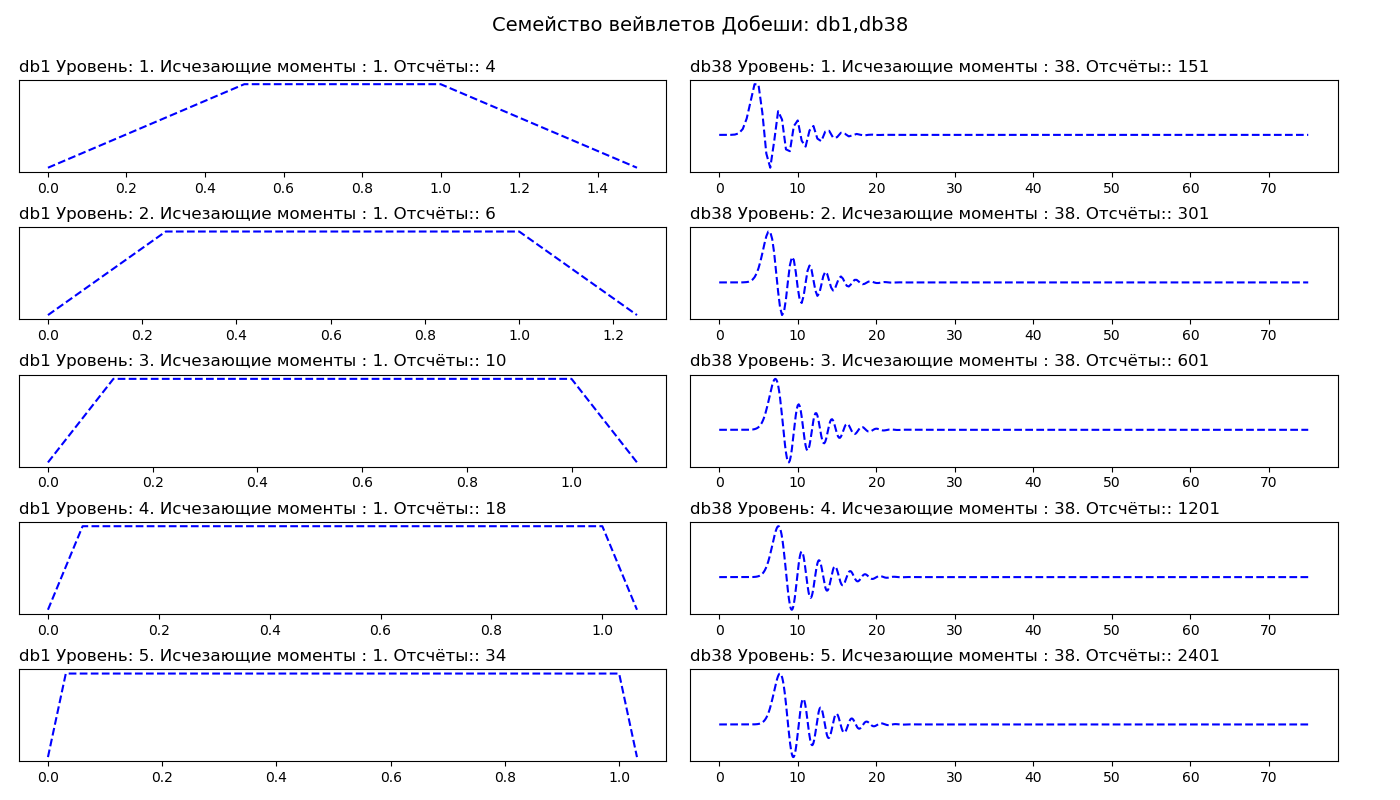
En la primera columna vemos las wavelets Daubeshi del primer orden (db1), en la segunda columna del trigésimo octavo orden (db38). Por lo tanto, db1 tiene un momento de extinción, y db38 tiene 38 momentos de extinción. El número de momentos de desaparición está relacionado con el orden de aproximación y la suavidad de la wavelet. Si una wavelet tiene P puntos de desaparición, puede aproximarse a polinomios de grado P - 1.

Las wavelets más suaves crean una aproximación de señal más suave y viceversa: las wavelets "cortas" siguen mejor los picos de la función aproximada. Al elegir una wavelet, también podemos indicar cuál debería ser el nivel de descomposición. Por defecto, PyWavelets selecciona el nivel máximo de descomposición posible para la señal de entrada. El nivel máximo de descomposición depende de la longitud de la señal de entrada y wavelet:


Para wavelet db1, nivel máximo de descomposición: 11
Para wavelet db38, nivel máximo de descomposición: 5

Para los valores obtenidos de los niveles máximos de descomposición de wavelets, consideramos la operación del filtro para eliminar el ruido de alta frecuencia:









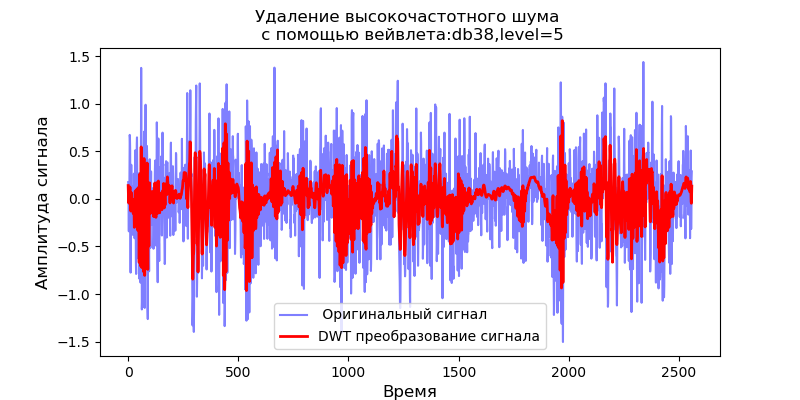
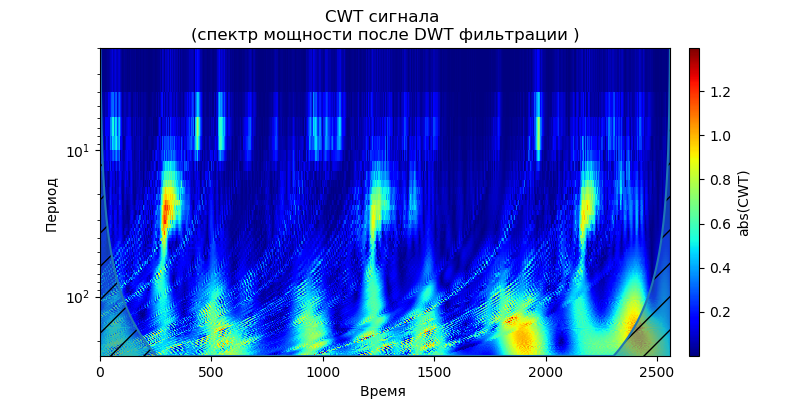
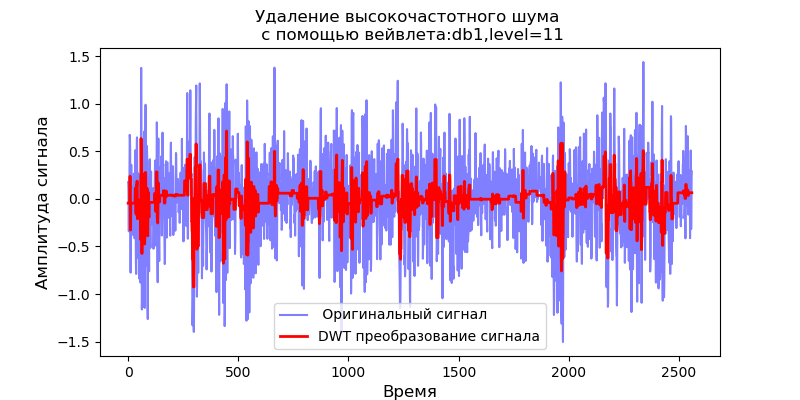
Se deduce de los escalogramas dados de las señales en la salida del filtro que, para la wavelet db38, la potencia máxima del espectro es seguida por regiones localizadas, para la wavelet db1, estas regiones desaparecen. Cabe señalar que, por ejemplo, la wavelet db38 puede aproximarse a una señal de polinomio de grado 37. Esto extiende la clasificación de las señales, por ejemplo, para identificar el mal funcionamiento del equipo por las señales de los sensores de vibración.

Dado que la señal después del filtro con la wavelet de Daubechies forma una serie temporal utilizando los coeficientes de aproximación y descomposición como características de la serie, es posible determinar el grado de proximidad de dicha serie, lo que simplifica enormemente su búsqueda y clasificación

Filtro de Kalman para eliminar el ruido de alta frecuencia

El filtro Kalman se usa ampliamente para filtrar el ruido en varios sistemas dinámicos. Considere un sistema dinámico con un vector de estado x.

$$$x = F \ cdot x + w (Q)$

donde F es la matriz de transición
w (Q) es un proceso aleatorio (ruido) con cero expectativas matemáticas y una matriz de covarianza Q.

Observaremos las transiciones de estado del sistema con un error de medición conocido en cada momento del tiempo. Eliminar el ruido usando el método de Kalman consta de dos pasos: extrapolación y corrección, se ve así.

Establezca los parámetros del sistema:

Matriz Q de covarianza de ruido (covarianza de ruido de proceso).
H es la matriz de observación (medición).
R - covarianza del ruido de observación (covarianza del ruido de medición).
P = Q es el valor inicial de la matriz de covarianza para el vector de estado.
z (t) es el estado observado del sistema.
x = z (0) es el valor inicial de la evaluación del estado del sistema.

Para cada observación z, calcularemos el estado filtrado x
y para esto realizamos los siguientes pasos.

• paso 1: extrapolación
1. extrapolación (predicción) del estado del sistema
$$$x = F \ cdot x$
2. calcular la matriz de covarianza para el vector de estado extrapolado
$$$F = F \ cdot P \ cdot F ^ {T} + Q$

• paso 2: corrección
1. calcular el vector de error, la desviación de la observación del estado esperado
$$$y = z-H \ cdot x$
2. calcular la matriz de covarianza para el vector de desviación (vector de error)
$$$S = H \ cdot P \ cdot H ^ {T} + R$
3. calcular las ganancias de Kalman
$$$K = P \ cdot H \ cdot H ^ {T} \ cdot S ^ {- 1}$
4. corrección de la estimación vectorial del estado
$$$x = x + K \ cdot y$
5. corregimos la matriz de covarianza para estimar el vector de estado del sistema
$$$P = (I-K \ cdot H) \ cdot P$




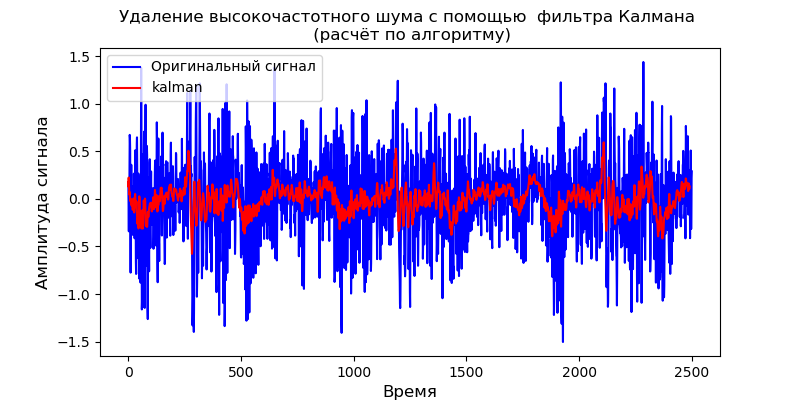
Para el modelo dinámico dado, puede usar la biblioteca pyKalman:






El filtro Kalman elimina bien el ruido de alta frecuencia, sin embargo, no permite cambiar la forma de la señal de salida.

Método de media móvil

Al determinar la dirección principal de los cambios en una secuencia fuertemente oscilante, surge el problema de suavizarlo utilizando el método de la media móvil. Estas pueden ser las lecturas del sensor de nivel de combustible en el automóvil o, como en nuestro caso, los datos de los sensores de alta frecuencia con respecto a la degradación acelerada de los rodamientos. El problema puede considerarse como la restauración de alguna secuencia r sobre la cual se superpuso el ruido.

Media móvil simple para abreviar: SMA (Media móvil simple). Para calcular el valor del filtro actual $$$r_ {i}$solo promediamos los n elementos anteriores de la secuencia, por lo que el filtro comienza a funcionar con el elemento de secuencia n.

$$$r_ {i} = \ frac {1} {n} \ cdot \ sum_ {j = 1} ^ {n} y _ {(i-j)}; i> n$






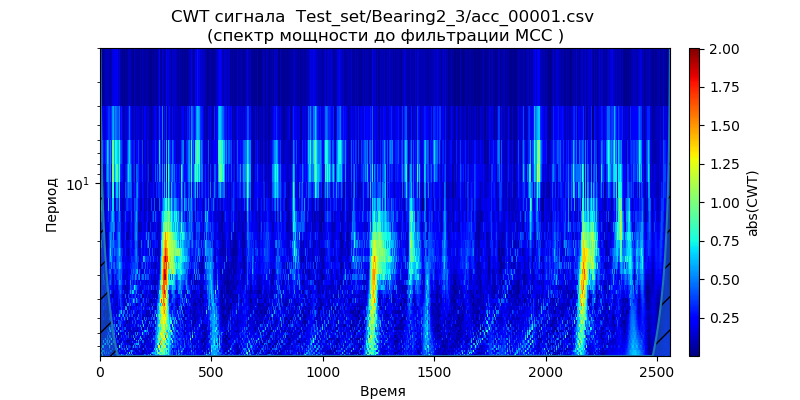
Como se desprende del escalograma, el método SMA no limpia la señal del ruido de alta frecuencia, y
como se mencionó anteriormente se utiliza para alisar.

Conclusiones:

1. Usando el módulo de escalagrama, se obtuvieron escalogramas wavelet CWT de tres señales de sensor de vibración de prueba para diferentes condiciones de prueba para rodamientos del mismo tipo. Según los datos del escalograma, se seleccionó una señal con signos claramente expresados ​​de degradación tardía. Esta señal se utilizó para demostrar el funcionamiento de los filtros en todos los ejemplos dados.
2. Se consideran los métodos de la biblioteca PyWavelets para la deconstrucción DWT y la restauración de la señal del sensor de vibración utilizando los módulos pywt.dwt (), pywt.idwt () y el módulo pywt.wavedec () para un nivel de wavelet dado.
3. Los ejemplos muestran las características de la aplicación del módulo pywt.threshol () para filtrar los coeficientes de refinamiento de DWT, que son responsables de la parte de alta frecuencia del espectro utilizando funciones de umbral para un valor de umbral dado.
4. Se consideran los efectos de la wavelet antiderivada DWT en la forma de una señal libre de ruido.
5. Se obtiene un modelo de filtro Kalman para un medio dinámico, el modelo se prueba con la señal de prueba del sensor de vibración. La gráfica de eliminación de ruido es la misma que la obtenida usando el módulo pyKalman. La naturaleza del gráfico coincide con el escalograma.
6. .