
La traducción del artículo fue preparada especialmente para los estudiantes del curso "Algoritmos para desarrolladores" .
La ordenación piramidal (u ordenación del montón, HeapSort) es un método de clasificación de comparación basado en una estructura de datos como un montón binario. Es similar a ordenar por selección, donde primero buscamos el elemento máximo y lo ponemos al final. A continuación, repetimos la misma operación para los elementos restantes.
Primero definamos un árbol binario completo. Un árbol binario terminado es un árbol binario en el que cada nivel, con la posible excepción del último, tiene un conjunto completo de nodos, y todas las hojas se encuentran a la izquierda (Fuente Wikipedia ).
Un montón binario es un árbol binario completo en el que los elementos se almacenan en un orden especial: el valor en el nodo principal es mayor que (o menor que) los valores en sus dos nodos secundarios. La primera opción se llama max-heap, y la segunda es min-heap. Un montón se puede representar mediante un árbol binario o una matriz.
¿Por qué se utiliza la representación basada en matriz para el almacenamiento dinámico binario?
Dado que el montón binario es un árbol binario completo, se puede representar fácilmente como una matriz, y la representación basada en la matriz es eficiente en términos de consumo de memoria. Si el nodo padre se almacena en el índice I, el hijo izquierdo se puede calcular como 2 I + 1, y el hijo derecho se puede calcular como 2 I + 2 (siempre que la indexación comience en 0).
Algoritmo de clasificación piramidal en orden ascendente:
- Construir max-heap a partir de la entrada.
- En esta etapa, el elemento más grande se almacena en la raíz del montón. Reemplácelo con el último elemento del montón, y luego reduzca su tamaño en 1. Finalmente, convierta el árbol resultante en max-heap con una nueva raíz.
- Repita los pasos anteriores hasta que el tamaño del montón sea mayor que 1.
¿Cómo construir un montón?
El procedimiento de conversión de almacenamiento dinámico (en adelante denominado el procedimiento de almacenamiento dinámico) se puede aplicar a un nodo solo si sus nodos secundarios ya están convertidos. Por lo tanto, la conversión debe realizarse de abajo hacia arriba. Vamos a resolverlo con un ejemplo:
: 4, 10, 3, 5, 1 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) . heapify 1: 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) heapify 0: 10(0) / \ 5(1) 3(2) / \ 4(3) 1(4) heapify .
Recomendación: primero resuelva el problema de “PRÁCTICA” antes de continuar con la solución .
C ++
// C++ #include <iostream> using namespace std; // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { swap(arr[i], arr[largest]); // heapify(arr, n, largest); } } // , void heapSort(int arr[], int n) { // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // swap(arr[0], arr[i]); // heapify heapify(arr, i, 0); } } /* n*/ void printArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } // int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); }
Java
// Java public class HeapSort { public void sort(int arr[]) { int n = arr.length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } // public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6, 7}; int n = arr.length; HeapSort ob = new HeapSort(); ob.sort(arr); System.out.println("Sorted array is"); printArray(arr); } }
Pitón
# Python # i, arr[]. n - def heapify(arr, n, i): largest = i # Initialize largest as root l = 2 * i + 1 # left = 2*i + 1 r = 2 * i + 2 # right = 2*i + 2 # , if l < n and arr[i] < arr[l]: largest = l # , if r < n and arr[largest] < arr[r]: largest = r # , if largest != i: arr[i],arr[largest] = arr[largest],arr[i] # # heapify . heapify(arr, n, largest) # def heapSort(arr): n = len(arr) # max-heap. for i in range(n, -1, -1): heapify(arr, n, i) # for i in range(n-1, 0, -1): arr[i], arr[0] = arr[0], arr[i] # heapify(arr, i, 0) # arr = [ 12, 11, 13, 5, 6, 7] heapSort(arr) n = len(arr) print ("Sorted array is") for i in range(n): print ("%d" %arr[i]), # Mohit Kumra
Do sostenido
// C# using System; public class HeapSort { public void sort(int[] arr) { int n = arr.Length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int[] arr, int n, int i) { int largest = i; // int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int[] arr) { int n = arr.Length; for (int i=0; i<n; ++i) Console.Write(arr[i]+" "); Console.Read(); } // public static void Main() { int[] arr = {12, 11, 13, 5, 6, 7}; int n = arr.Length; HeapSort ob = new HeapSort(); ob.sort(arr); Console.WriteLine("Sorted array is"); printArray(arr); } } // // Akanksha Ra (Abby_akku)
Php
<?php // Php // i, // arr[]. n - function heapify(&$arr, $n, $i) { $largest = $i; // $l = 2*$i + 1; // = 2*i + 1 $r = 2*$i + 2; // = 2*i + 2 // if ($l < $n && $arr[$l] > $arr[$largest]) $largest = $l; // , if ($r < $n && $arr[$r] > $arr[$largest]) $largest = $r; // if ($largest != $i) { $swap = $arr[$i]; $arr[$i] = $arr[$largest]; $arr[$largest] = $swap; // heapify($arr, $n, $largest); } } // , function heapSort(&$arr, $n) { // ( ) for ($i = $n / 2 - 1; $i >= 0; $i--) heapify($arr, $n, $i); // for ($i = $n-1; $i >= 0; $i--) { // $temp = $arr[0]; $arr[0] = $arr[$i]; $arr[$i] = $temp; // heapify heapify($arr, $i, 0); } } /* n */ function printArray(&$arr, $n) { for ($i = 0; $i < $n; ++$i) echo ($arr[$i]." ") ; } // $arr = array(12, 11, 13, 5, 6, 7); $n = sizeof($arr)/sizeof($arr[0]); heapSort($arr, $n); echo 'Sorted array is ' . "\n"; printArray($arr , $n); // Shivi_Aggarwal ?>
Conclusión
: 5 6 7 11 12 13
Aquí está el código C anterior para referencia.
Observaciones:
La clasificación piramidal es un algoritmo perfectamente adecuado. Su implementación típica no es estable, pero se puede hacer como tal (ver aquí ).
Complejidad de tiempo: la complejidad de tiempo de heapify es O (Logn). La complejidad temporal de createAndBuildHeap () es O (n), y el tiempo de ejecución total de la ordenación piramidal es O (nLogn).
Aplicaciones de clasificación piramidal:
- Ordenar una matriz casi ordenada (o ordenada por K posiciones) ;
- k elementos más grandes (o más pequeños) en la matriz .
El algoritmo de clasificación piramidal tiene un uso limitado, porque Quicksort y Mergesort son mejores en la práctica. Sin embargo, la estructura de datos del montón en sí se usa con bastante frecuencia. Ver aplicaciones de estructura de datos de montón
Capturas de pantalla
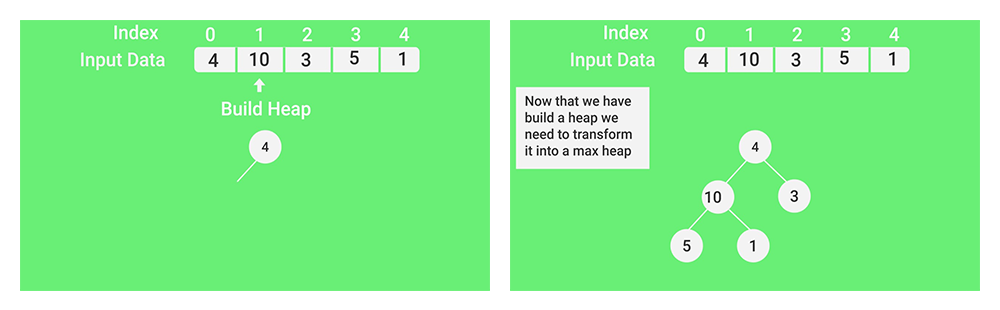
- (Ahora que hemos construido el montón, necesitamos convertirlo a max-heap)

- (En max-heap, el nodo primario siempre es mayor o igual que los nodos secundarios
10 más que 4. Por lo tanto, intercambiamos 4 y 10)
- (En max-heap, el nodo primario siempre es mayor o igual que los nodos secundarios
5 más 4. Por lo tanto, intercambiamos los lugares 5 y 4)

- (Intercambie el primer y el último nodo y elimine el último del montón)
Prueba de la pirámide
Otros algoritmos de ordenación en GeeksforGeeks / GeeksQuiz:
Clasificación rápida , clasificación por selección , clasificación por burbujas , clasificación por inserción , clasificación por fusión , clasificación por pirámide , clasificación por bits , clasificación por conteo , clasificación por bloques , clasificación por concha , clasificación por peine, clasificación por conteo con lista .
Taller de clasificación
Deje comentarios si encuentra algo incorrecto o si desea compartir información adicional sobre el tema discutido anteriormente.