
La ciencia de datos se está convirtiendo en una parte integral de cualquier actividad de marketing, y este libro es un retrato vivo de la transformación digital en marketing. El análisis de datos y los algoritmos inteligentes automatizan las tareas de marketing que requieren mucho tiempo. El proceso de toma de decisiones se está volviendo no solo más perfecto, sino también más rápido, lo cual es de gran importancia en un entorno competitivo en constante aceleración.
“Este libro es un retrato vivo de la transformación digital en marketing. Muestra cómo la ciencia de datos se está convirtiendo en una parte integral de cualquier actividad de marketing. Describe en detalle cómo los enfoques basados en análisis de datos y algoritmos inteligentes contribuyen a la automatización profunda de las tareas de marketing tradicionalmente intensivas en mano de obra. El proceso de toma de decisiones se está volviendo no solo más avanzado, sino también más rápido, lo cual es importante en nuestro entorno competitivo en constante aceleración. Este libro debe ser leído por especialistas en procesamiento de datos y especialistas en marketing, y es mejor que lo lean juntos ”. Andrey Sebrant, Director de Marketing Estratégico, Yandex.
Extracto 5.8.3. Modelos de factores ocultos
En los algoritmos de filtrado conjunto discutidos hasta ahora, la mayoría de los cálculos se basan en los elementos individuales de la matriz de calificación. Los métodos basados en la proximidad evalúan las calificaciones faltantes directamente de los valores conocidos en la matriz de calificación. Los métodos basados en modelos agregan una capa de abstracción en la parte superior de la matriz de calificación, creando un modelo predictivo que captura ciertos patrones de relaciones entre usuarios y elementos, pero la capacitación del modelo aún depende en gran medida de las propiedades de la matriz de calificación. Como resultado, estas técnicas de filtrado colaborativo generalmente enfrentan los siguientes problemas:
La matriz de calificación puede contener millones de usuarios, millones de elementos y miles de millones de calificaciones conocidas, lo que crea serios problemas de complejidad computacional y escalabilidad.
La matriz de calificación suele ser muy escasa (en la práctica, puede faltar aproximadamente el 99% de las calificaciones). Esto afecta la estabilidad computacional de los algoritmos de recomendación y conduce a estimaciones poco confiables cuando el usuario o elemento no tiene vecinos realmente similares. Este problema a menudo se ve exacerbado por el hecho de que la mayoría de los algoritmos básicos están orientados al usuario o al elemento, lo que limita su capacidad de registrar todo tipo de similitudes y relaciones disponibles en la matriz de calificación.
Los datos en la matriz de calificación generalmente están fuertemente correlacionados debido a las similitudes entre usuarios y elementos. Esto significa que las señales disponibles en la matriz de clasificación no solo son escasas, sino también redundantes, lo que contribuye a la exacerbación del problema de escalabilidad.
Las consideraciones anteriores indican que la matriz de calificación original puede no ser la representación más óptima de las señales, y se deben considerar otras representaciones alternativas que sean más adecuadas para el filtrado conjunto. Para explorar esta idea, volvamos al punto de partida y reflexionemos un poco sobre la naturaleza de los servicios de recomendación. De hecho, el servicio de recomendación puede considerarse como un algoritmo que predice clasificaciones basadas en alguna medida de similitud entre el usuario y el elemento:
Una forma de determinar esta medida de similitud es utilizar el enfoque de factor oculto y asignar usuarios y elementos a puntos en algún espacio k-dimensional para que cada usuario y cada elemento estén representados por un vector k-dimensional:
Los vectores deben construirse de manera que las dimensiones correspondientes p y q sean comparables entre sí. En otras palabras, cada dimensión puede considerarse como un signo o concepto, es decir, puj es una medida de proximidad del usuario u y el concepto j, y qij, respectivamente, es una medida del elemento i y el concepto j. En la práctica, estas dimensiones a menudo se interpretan como géneros, estilos y otros atributos que se aplican simultáneamente a usuarios y elementos. La similitud entre el usuario y el elemento y, en consecuencia, la calificación se puede definir como el producto de los vectores correspondientes:

Como cada calificación se puede descomponer en un producto de dos vectores que pertenecen a un espacio conceptual que no se observa directamente en la matriz de calificación original, pyq se denominan factores ocultos. El éxito de este enfoque abstracto, por supuesto, depende completamente de cómo se determinan y construyen los factores ocultos. Para responder a esta pregunta, observamos que la expresión 5.92 se puede reescribir en forma de matriz de la siguiente manera:
donde P es la matriz n × k ensamblada a partir de los vectores p, y Q es la matriz m × k ensamblada a partir de los vectores q, como se muestra en la Fig. 5.13. El objetivo principal de un sistema de filtrado conjunto suele ser minimizar los errores de predicción de la calificación, lo que le permite determinar directamente el problema de optimización en relación con la matriz de factores ocultos:
Suponiendo que el número de dimensiones ocultas k es fijo yk ≤ ny k ≤ m, el problema de optimización 5.94 se reduce al problema de aproximación de bajo rango, que consideramos en el Capítulo 2. Para demostrar el enfoque de la solución, supongamos por un momento que la matriz de calificación está completa. En este caso, el problema de optimización tiene una solución analítica en términos de la Descomposición de valor singular (SVD) de la matriz de calificación. En particular, utilizando el algoritmo SVD estándar, la matriz se puede descomponer en el producto de tres matrices:
donde U es la matriz n × n ortonormalizada por columnas, Σ es la matriz diagonal n × m, y V es la matriz m × m ortonormalizada por columnas. Se puede obtener una solución óptima al problema 5.94 en términos de estos factores, truncados a las k dimensiones más significativas:
En consecuencia, los factores ocultos que son óptimos en términos de precisión de predicción se pueden obtener por descomposición singular, como se muestra a continuación:
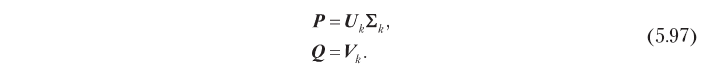
Este modelo de factor oculto basado en SVD ayuda a resolver los problemas de co-filtrado descritos al comienzo de esta sección. Primero, reemplaza la gran matriz de clasificación n × m con matrices de factores n × k y m × k, que generalmente son mucho más pequeñas, porque en la práctica el número óptimo de dimensiones ocultas k es a menudo pequeño. Por ejemplo, hay un caso en el que la matriz de calificación con 500,000 usuarios y 17,000 elementos pudo aproximarse bastante bien usando 40 mediciones [Funk, 2016]. Además, SVD elimina la correlación en la matriz de calificación: las matrices de factores latentes definidas por 5.97 son ortonormales en columnas, es decir, las dimensiones ocultas no están correlacionadas. Si, lo cual suele ser cierto en la práctica, SVD también resuelve el problema de la escasez, porque la señal presente en la matriz de clasificación original se concentra efectivamente (recuerde que seleccionamos k dimensiones con la energía de señal más alta), y la matriz de factores ocultos no es escasa. La figura 5.14 ilustra esta propiedad. El algoritmo de proximidad basado en el usuario (5.14, a) contrae vectores de calificación dispersos para un elemento dado y un usuario determinado para obtener una puntuación de calificación. El modelo de factor oculto (5.14, b), por el contrario, estima la clasificación por convolución de dos vectores de dimensión reducida y con una densidad de energía más alta.

El enfoque que se acaba de describir parece una solución coherente al problema de los factores ocultos, pero de hecho tiene un serio inconveniente debido al supuesto de que la matriz de calificación está completa. Si la matriz de calificación es escasa, lo cual es casi siempre el caso, el algoritmo SVD estándar no se puede aplicar directamente, ya que no puede procesar elementos faltantes (indefinidos). La solución más simple en este caso es completar las calificaciones faltantes con algún valor predeterminado, pero esto puede conducir a un sesgo grave en el pronóstico. Además, es computacionalmente ineficiente porque la complejidad computacional de dicha solución es igual a la complejidad SVD para la matriz n × m completa, mientras que es deseable tener un método con complejidad proporcional al número de clasificaciones conocidas. Estos problemas pueden resolverse utilizando los métodos alternativos de descomposición descritos en las siguientes secciones.
5.8.3.1. Descomposición ilimitada
El algoritmo SVD estándar es una solución analítica para el problema de aproximación de bajo rango. Sin embargo, este problema puede considerarse como un problema de optimización, y también se le pueden aplicar métodos de optimización universal. Uno de los enfoques más simples es usar el método de descenso de gradiente para refinar iterativamente los valores de factores ocultos. El punto de partida es la definición de la función de costo J como el error de pronóstico residual:
Tenga en cuenta que esta vez no imponemos restricciones, como la ortogonalidad, en la matriz de factores ocultos. Calculando el gradiente de la función de costo con respecto a factores ocultos, obtenemos el siguiente resultado:
donde E es la matriz de error residual:
El algoritmo de descenso de gradiente minimiza la función de costo al moverse en cada paso en la dirección negativa del gradiente. Por lo tanto, puede encontrar factores ocultos que minimizan el error al cuadrado de la predicción de calificación cambiando iterativamente las matrices P y Q para que converjan, de acuerdo con las siguientes expresiones:

donde α es la velocidad de aprendizaje. La desventaja del método de descenso de gradiente es la necesidad de calcular la matriz completa de errores residuales y cambiar simultáneamente todos los valores de los factores ocultos en cada iteración. Un enfoque alternativo, que puede ser más adecuado para matrices grandes, es el descenso de gradiente estocástico [Funk, 2016]. El algoritmo de descenso de gradiente estocástico utiliza el hecho de que el error de pronóstico total J es la suma de los errores para elementos individuales de la matriz de calificación; por lo tanto, el gradiente general J puede aproximarse por un gradiente en un punto de datos y los factores ocultos pueden cambiarse en función de los elementos. La implementación completa de esta idea se muestra en el algoritmo 5.1.

La primera etapa del algoritmo es la inicialización de la matriz de factores ocultos. La elección de estos valores iniciales no es muy importante, pero en este caso, se elige una distribución uniforme de la energía de las clasificaciones conocidas entre los factores ocultos generados aleatoriamente. Luego, el algoritmo optimiza secuencialmente las dimensiones del concepto. Para cada medición, recorre repetidamente todas las clasificaciones en el conjunto de entrenamiento, predice cada clasificación utilizando los valores actuales de los factores ocultos, estima el error y corrige los valores de los factores de acuerdo con las expresiones 5.101. La optimización de la medición se completa cuando se cumple la condición de convergencia, después de lo cual el algoritmo pasa a la siguiente medición.
El algoritmo 5.1 ayuda a superar las limitaciones del método SVD estándar. Optimiza los factores ocultos al recorrer puntos de datos individuales y, por lo tanto, evita problemas con calificaciones faltantes y operaciones algebraicas con matrices gigantes. El enfoque iterativo también hace que el descenso de gradiente estocástico sea más conveniente para aplicaciones prácticas que el descenso de gradiente, que modifica matrices completas usando las expresiones 5.101.
EJEMPLO 5.6
De hecho, un enfoque basado en factores ocultos es un grupo completo de métodos de enseñanza de representaciones que pueden identificar patrones implícitos en la matriz de calificación y representarlos explícitamente en forma de conceptos. A veces, los conceptos tienen una interpretación completamente significativa, especialmente los de alta energía, aunque esto no significa que todos los conceptos siempre tengan un significado significativo. Por ejemplo, aplicar el algoritmo de descomposición matricial a una base de datos de clasificaciones de películas puede crear factores que se corresponden aproximadamente con las dimensiones psicográficas, como el melodrama, la comedia, el horror, etc. Vamos a ilustrar este fenómeno con un pequeño ejemplo numérico que utiliza la matriz de clasificación de la tabla. 5.3:

Primero, reste el promedio global μ = 2.82 de todos los elementos para centrar la matriz, y luego ejecute el algoritmo 5.1 con k = 3 mediciones ocultas y la tasa de aprendizaje α = 0.01 para obtener las siguientes dos matrices de factores:

Cada fila en estas matrices corresponde a un usuario o una película, y los 12 vectores de fila se muestran en la Fig. 5.15. Tenga en cuenta que los elementos en la primera columna (el primer vector de conceptos) tienen los valores más grandes, y los valores en las columnas posteriores disminuyen gradualmente. Esto se explica por el hecho de que el primer vector de concepto captura tanta energía de señal como es posible capturar usando una medición, el segundo vector de concepto captura solo una parte de la energía residual, etc. Además, tenga en cuenta que el primer concepto puede interpretarse semánticamente como el eje dramático - película de acción, donde la dirección positiva corresponde al género de la película de acción, y la negativa - al género del drama. Las calificaciones en este ejemplo están altamente correlacionadas, por lo que se puede ver claramente que los primeros tres usuarios y las primeras tres películas tienen grandes valores negativos en el primer concepto vectorial (películas de drama y usuarios a quienes les gustan tales películas), mientras que los últimos tres usuarios y los últimos tres Las películas tienen grandes significados positivos en la misma columna (películas de acción y usuarios que prefieren este género). La segunda dimensión en este caso particular corresponde principalmente al sesgo del usuario o elemento, que puede interpretarse como un atributo psicográfico (¿crítica de los juicios del usuario? ¿Popularidad de la película?). Otros conceptos pueden considerarse como ruido.
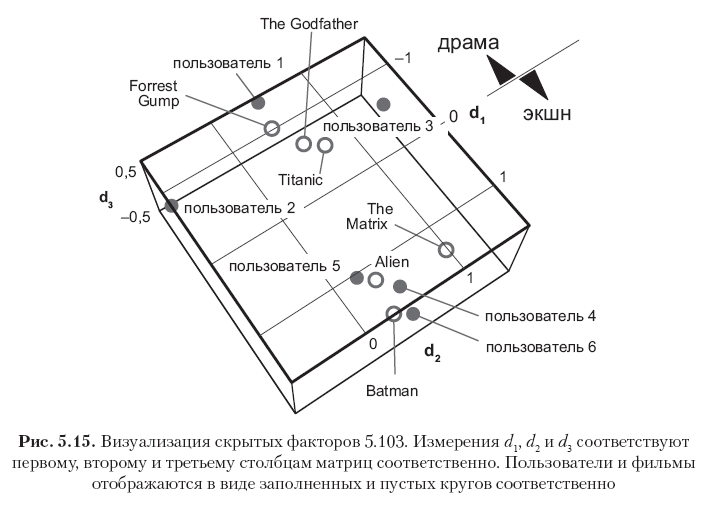
La matriz de factores resultante no es completamente ortogonal en las columnas, pero tiende a ser ortogonal, porque esto se deduce de la optimización de la solución SVD. Esto se puede ver mirando los productos de PTP y QTQ, que están cerca de las matrices diagonales:
Las matrices 5.103 son esencialmente un modelo predictivo que se puede utilizar para evaluar las clasificaciones conocidas y faltantes. Se pueden obtener estimaciones multiplicando dos factores y sumando el promedio global:
Los resultados reproducen con precisión lo conocido y predicen las calificaciones faltantes de acuerdo con las expectativas intuitivas. La precisión de las estimaciones se puede aumentar o disminuir cambiando el número de mediciones, y el número óptimo de mediciones se puede determinar en la práctica mediante una verificación cruzada y eligiendo un compromiso razonable entre la complejidad y la precisión computacional.
»Se puede encontrar más información sobre el libro en
el sitio web del editor»
Contenidos»
ExtractoCupón de 25% de descuento para vendedores ambulantes -
Machine LearningTras el pago de la versión en papel del libro, se envía un libro electrónico por correo electrónico.