Conferencia "Fundamentos del procesamiento de señales digitales"

Hola a todos!

A menudo las personas recurren a mí con preguntas sobre tareas del campo del procesamiento de señales digitales (DSP). Cuento en detalle los matices, sugiero las fuentes de información necesarias. Pero todos los oyentes, como lo ha demostrado el tiempo, carecen de tareas prácticas y ejemplos en el proceso de aprendizaje de esta área. En este sentido, decidí escribir un breve curso interactivo sobre procesamiento de señales digitales y ponerlo en el dominio público .

La mayor parte del material de capacitación para la presentación visual e interactiva se implementa utilizando el Jupyter Notebook . Se supone que el lector tiene un conocimiento básico del campo de las matemáticas superiores, así como un pequeño dominio del lenguaje de programación Python.

Lista de conferencias

Este curso contiene materiales en forma de conferencias terminadas sobre diversos temas del campo del procesamiento de señales digitales. Los materiales se presentan utilizando bibliotecas de Python (paquetes numpy, scipy, matplotlib, etc.). La información básica para este curso fue tomada de mis conferencias, que yo, como estudiante graduado, les di a los estudiantes del Instituto de Energía de Moscú (NRU MEI). Parte de la información de estas conferencias se usó en seminarios de capacitación en el Centro de Electrónica Contemporánea , donde actué como profesor. Además, este material incluye la traducción de varios artículos científicos, compilación de información de fuentes confiables y literatura sobre procesamiento de señales digitales, así como documentación oficial sobre paquetes de aplicaciones y funciones integradas de las bibliotecas scipy y numpy de Python.

Para los usuarios de MATLAB (GNU Octave), dominar el material desde el punto de vista del código del programa no es difícil, ya que las funciones principales y sus atributos son en gran medida idénticos y similares a los métodos de las bibliotecas de Python.

Todos los materiales están agrupados por los principales temas del procesamiento de señales digitales:

1. Señales: analógicas, discretas, digitales. Conversión Z
2. Transformada de Fourier: señal de amplitud y fase, DFT y FFT,
3. Convolución y correlación. Convolución lineal y cíclica. Convolución rápida
4. Procesos aleatorios. Ruido blanco Función de densidad de probabilidad
5. Señales deterministas. Modulación: AM, FM, FM, LFM. Manipulación
6. Filtrado de señal: IIR, filtros FIR
7. Funciones de ventana en tareas de filtrado. Detección de señales débiles.
8. Muestreo: diezmado e interpolación. Filtros CIC, filtros de media móvil

La lista de conferencias es suficiente pero, por supuesto, incompleta para un conocimiento introductorio del campo de DSP. Con tiempo libre, planeo apoyar y desarrollar este proyecto.

Donde encontrar

Todos los materiales son absolutamente gratuitos y están disponibles como repositorio abierto en mi github como un proyecto de código abierto . Los materiales se presentan en dos formatos: en forma de cuadernos Jupyter para trabajo interactivo, estudio y edición, y en forma de archivos HTML compilados a partir de estos cuadernos (después de descargarlos de Github tienen un formato bastante adecuado para leer e imprimir).

La siguiente es una descripción muy breve de las secciones del curso con explicaciones breves, términos y definiciones. La información básica está disponible en las conferencias iniciales, ¡aquí hay solo una breve descripción!

Señales Conversión Z

Sección introductoria, que contiene información básica sobre los tipos de señales. Se introduce el concepto de secuencia discreta, función delta y función Heaviside (salto de unidad).

Todas las señales de acuerdo con el método de presentación en el conjunto se pueden dividir en cuatro grupos:

• analógico: se describen mediante funciones continuas en el tiempo,
• discreto: se interrumpe a tiempo con un paso especificado por muestreo,
• cuantizado: tener un conjunto de niveles finitos (generalmente en amplitud),
• digital: una combinación de las propiedades de las señales discretas y cuantificadas.

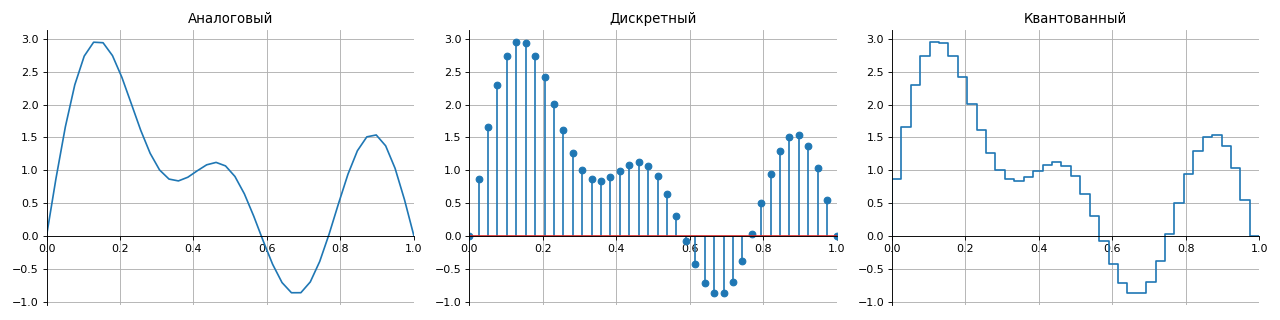
Para la reconstrucción correcta de una señal analógica de una señal digital sin distorsión y pérdida, se utiliza el teorema de muestreo conocido como el teorema de Kotelnikov (Nyquist-Shannon) .

Cualquier señal continua con un espectro limitado puede restaurarse de manera única y sin pérdida por sus muestras discretas tomadas con una frecuencia estrictamente mayor que el doble de la frecuencia superior del espectro de una señal continua.

Tal interpretación es válida siempre que la función continua del tiempo ocupe una banda de frecuencia de 0 al valor de la frecuencia superior. Si los pasos de cuantización y discretización se eligen incorrectamente, la señal se distorsionará de analógica a discreta.

También en esta sección, se describe la transformación Z y sus propiedades, y se muestra la representación de secuencias discretas en la forma Z.

Ejemplo de una secuencia discreta finita:

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0} 

.
Un ejemplo de la misma secuencia en forma de Z:

X (z) = 2 + z ^-1 - 2z ^-2 + 2z ^-4 + 3z ^-5 + 1z ^-6

Transformada de Fourier. Propiedades DFT y FFT

Esta sección describe el concepto del dominio de tiempo y frecuencia de una señal. Se introduce la definición de la transformada discreta de Fourier (DFT). Se consideran los DFT directos e inversos y sus propiedades principales. Se muestra la transición del DFT al algoritmo de transformación rápida de Fourier (FFT) en la base 2 (algoritmos de diezmado en frecuencia y tiempo). Reflejó la efectividad de FFT en comparación con DFT.

En particular, esta sección describe el paquete de Python scipy.ffpack para calcular varias transformadas de Fourier (seno, coseno, directo, inverso, multidimensional, real).

¡La transformación de Fourier le permite representar cualquier función como un conjunto de señales armónicas! La transformación de Fourier es la base de los métodos de convolución y el diseño de correlacionadores digitales, se usa activamente en el análisis espectral y se usa cuando se trabaja con números largos.

Características de los espectros de señales discretas:
1. La densidad espectral de una señal discreta es una función periódica con un período igual a la frecuencia de muestreo.
2. Si la secuencia discreta es real , entonces el módulo de densidad espectral de dicha secuencia es una función par , y el argumento es una función de frecuencia impar .

Espectro de señal armónica:

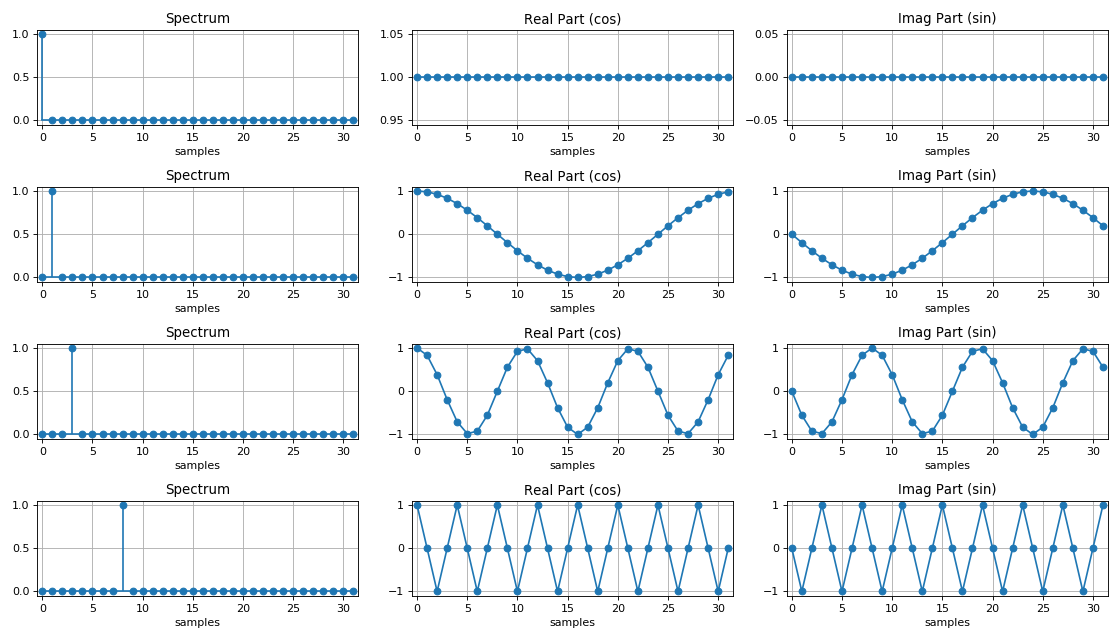
Comparación de la eficacia de DFT y FFT

La eficiencia del algoritmo FFT y el número de operaciones realizadas linealmente depende de la longitud de secuencia N:


Como puede ver, cuanto mayor sea la duración de la conversión, mayores serán los ahorros en recursos informáticos (en términos de velocidad de procesamiento o la cantidad de unidades de hardware).

Cualquier forma de onda arbitraria puede representarse como un conjunto de señales armónicas de diferentes frecuencias. En otras palabras, una señal de forma compleja en el dominio del tiempo tiene un conjunto de muestras complejas en el dominio de la frecuencia, que se denominan * armónicos *. Estas muestras expresan la amplitud y la fase del efecto armónico a una frecuencia específica. Cuanto mayor es el conjunto de armónicos en el dominio de la frecuencia, más exactamente aparece la forma de onda compleja.

Convolución y correlación

Esta sección presenta el concepto de correlación y convolución para secuencias discretas aleatorias y deterministas. Se muestra la relación entre las funciones de autocorrelación y correlación cruzada con convolución. Se describen las propiedades de convolución, en particular, se consideran los métodos de convolución lineal y cíclica de una señal discreta con análisis detallado sobre el ejemplo de una secuencia discreta. Además, se muestra un método para calcular la convolución "rápida" utilizando algoritmos FFT.

En problemas reales, a menudo se plantea la cuestión sobre el grado de similitud de un proceso con otro o sobre la independencia de un proceso de otro. En otras palabras, se requiere determinar la relación entre las señales, es decir, encontrar una correlación . Los métodos de correlación se utilizan en una amplia gama de tareas: búsqueda de señales, visión por computadora y procesamiento de imágenes, en problemas de radar para determinar las características de los objetivos y determinar la distancia a un objeto. Además, la correlación se usa para buscar señales débiles en el ruido.

La convolución describe la interacción de las señales entre sí. Si una de las señales es la respuesta al impulso del filtro, entonces la convolución de la secuencia de entrada con la respuesta al impulso no es más que una reacción del circuito a la acción de entrada. En otras palabras, la señal resultante refleja el paso de la señal a través del filtro.

La función de autocorrelación (ACF) se utiliza en la codificación de información. La elección de la secuencia de codificación de acuerdo con los parámetros de longitud, frecuencia y forma se debe en gran medida a las propiedades de correlación de esta secuencia. La mejor secuencia de código tiene la menor probabilidad de detección u operación falsa (para detectar señales, para dispositivos de umbral) o sincronización falsa (para transmitir y recibir secuencias de código).

Esta sección presenta una tabla que compara la efectividad de la convolución rápida y la convolución calculada por la fórmula directa (por el número de multiplicaciones reales).

Como puede ver, para longitudes de FFT de hasta 64, la convolución rápida pierde con el método directo. Sin embargo, con un aumento en la longitud de FFT, los resultados cambian en la dirección opuesta: una convolución rápida comienza a superar al método directo. Obviamente, cuanto más larga sea la FFT, mejor será la ganancia en el método de frecuencia.

Señales aleatorias y ruido

En esta sección, se introduce el concepto de señales aleatorias, densidad de probabilidad, ley de distribución aleatoria. Se consideran los momentos matemáticos: media (expectativa matemática) y varianza (o la raíz de esta cantidad es la desviación estándar). También en esta sección, la distribución normal y el concepto relacionado de ruido blanco se consideran la principal fuente de ruido (interferencia) durante el procesamiento de la señal.

Una señal aleatoria es una función del tiempo cuyos valores no se conocen de antemano y solo pueden predecirse con cierta probabilidad . Las características principales de las señales aleatorias incluyen:

• ley de distribución (el tiempo de residencia relativo del valor de la señal en un cierto intervalo),
• distribución espectral de potencia de señal.

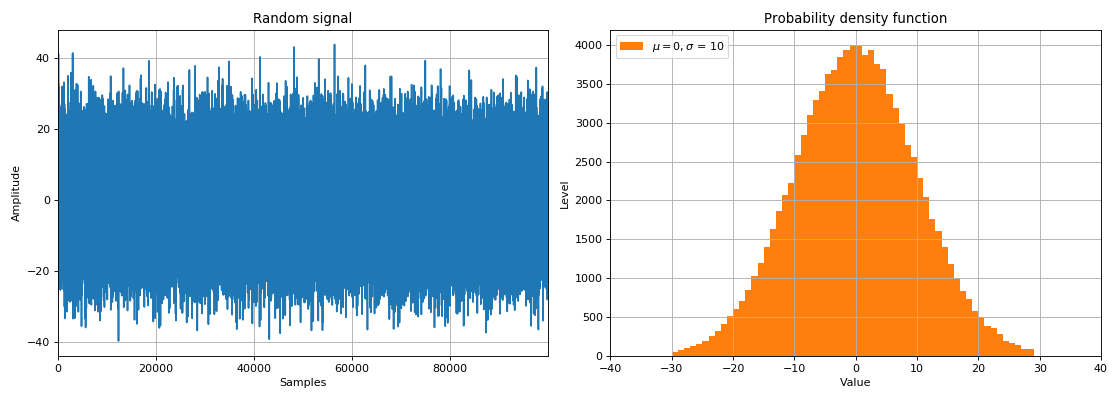
En las tareas DSP, las señales aleatorias se dividen en dos clases:

• ruido: fluctuaciones aleatorias que consisten en un conjunto de diferentes frecuencias y amplitudes,
• señales que transportan información, para cuyo procesamiento es necesario recurrir a métodos probabilísticos.

Usando variables aleatorias, podemos simular el efecto de un medio real en el paso de una señal desde una fuente a un receptor de datos. Cuando una señal pasa a través de algún enlace ruidoso, el llamado ruido blanco se agrega a la señal. Como regla general, la densidad espectral de dicho ruido se distribuye uniformemente (por igual) en todas las frecuencias, y los valores de ruido en el dominio del tiempo se distribuyen normalmente (ley de distribución gaussiana). Dado que el ruido blanco se agrega físicamente a las amplitudes de la señal en las muestras de tiempo seleccionadas, se denomina ruido gaussiano blanco aditivo (AWGN).

Señales, Modulación y Manipulación

Esta sección muestra los métodos básicos para cambiar uno o más parámetros de una señal armónica. Se introducen los conceptos de amplitud, frecuencia y modulación de fase. En particular, se destaca la modulación de frecuencia lineal utilizada en problemas de radar. Se muestran las principales características de las señales, los espectros de las señales moduladas dependiendo de los parámetros de modulación.



Por conveniencia, se ha creado un conjunto de funciones en Python que implementa los tipos de modulación anteriores. Ejemplo de implementación de señal chirp:

 def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs): """ Create Chirp signal Parameters ---------- amp : float Signal magnitude beta : float Modulation bandwidth: beta < N for complex, beta < 0.5N for real freq : float or int Linear frequency of signal period : integer Number of points for signal (same as period) kwargs : bool Complex signal if is_complex = True Modulated by half-sine wave if is_modsine = True """ is_complex = kwargs.get('is_complex', False) is_modsine = kwargs.get('is_modsine', False) t = np.linspace(0, 1, period) tt = np.pi * (freq * t + beta * t ** 2) if is_complex is True: res = amp * (np.cos(tt) + 1j * np.sin(tt)) else: res = amp * np.cos(tt) if is_modsine is True: return res * np.sin(np.pi * t) return res 

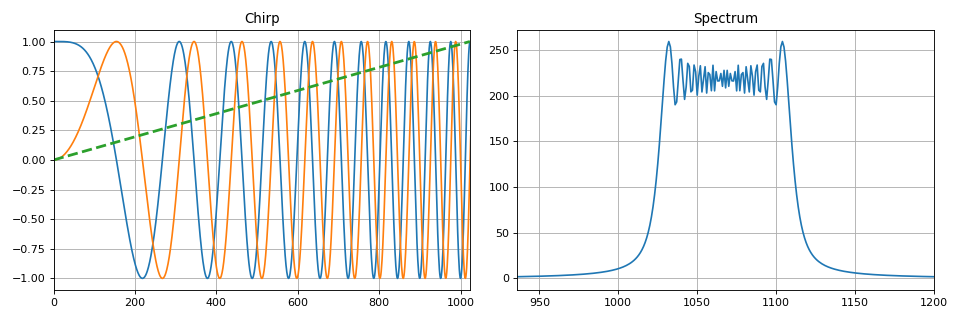
También en esta sección de la teoría de la transmisión de mensajes discretos se describen tipos de modulación digital: se describen manipulaciones. Como en el caso de las señales analógicas, las secuencias armónicas digitales se pueden manipular en amplitud, fase y frecuencia (o varios parámetros a la vez).

Filtros digitales - IIR y FIR

Una sección suficientemente grande dedicada al filtrado digital de secuencias discretas. En las tareas de procesamiento de señal digital, los datos fluyen a través de circuitos llamados filtros . Los filtros digitales, como los analógicos, tienen diferentes características: frecuencia: respuesta de frecuencia, respuesta de fase, tiempo: respuesta de impulso, así como la característica de transferencia del filtro. Los filtros digitales se utilizan principalmente para mejorar la calidad de la señal, para aislar una señal de una secuencia de datos o para degradar señales no deseadas, para suprimir ciertas señales en las secuencias de muestras entrantes.



La sección enumera las principales ventajas y desventajas de los filtros digitales (en comparación con los analógicos). Se introduce el concepto de impulso y características de transferencia del filtro. Se consideran dos clases de filtros: con una respuesta de impulso infinita (IIR) y una respuesta de impulso finita (FIR). Se muestra un método para diseñar filtros en forma canónica y directa . Para los filtros FIR, se considera la cuestión de cómo cambiar a una forma recursiva.



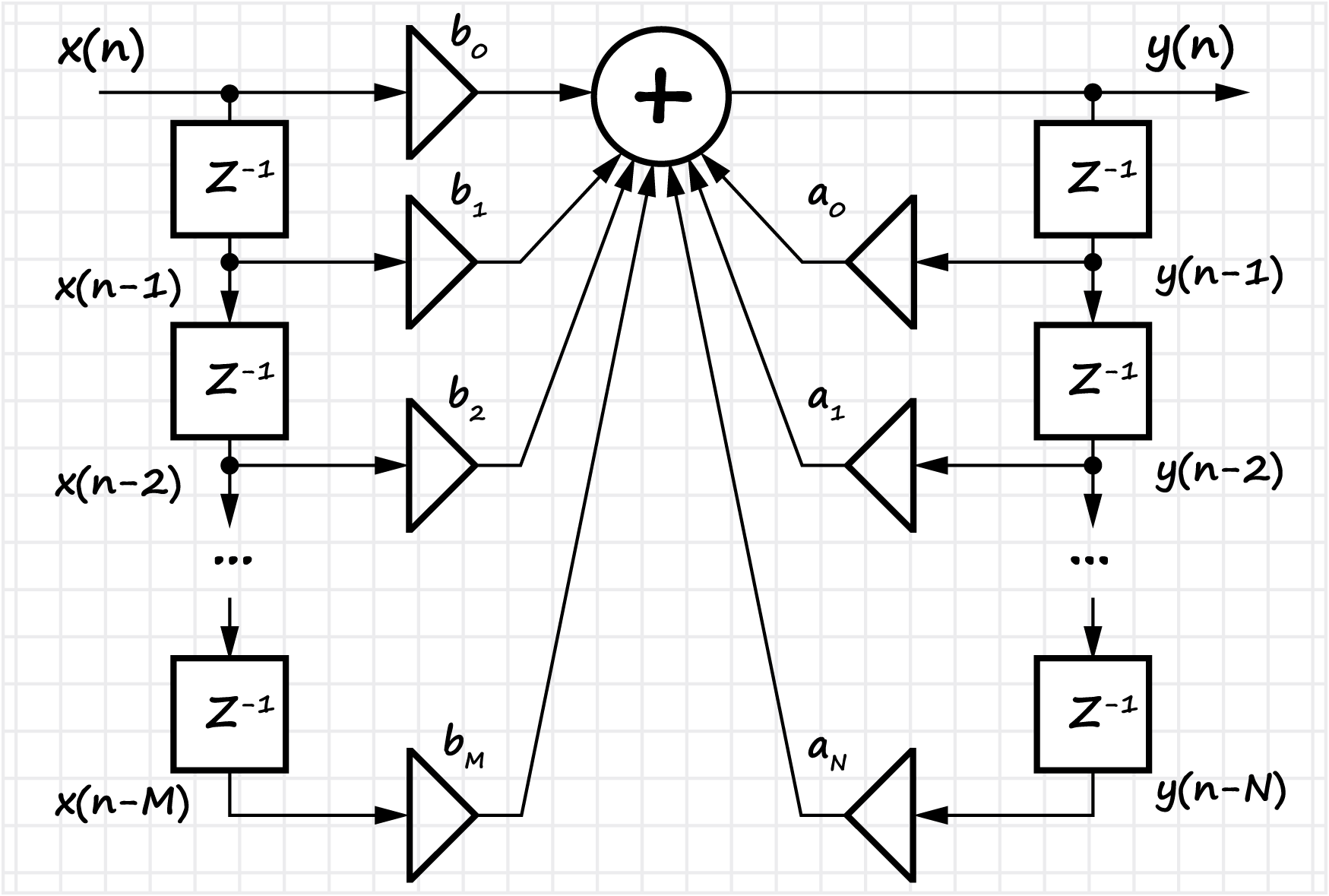
Para los filtros FIR, el proceso de diseño del filtro se muestra desde la etapa de desarrollo de las especificaciones técnicas (con los parámetros principales indicados), hasta la implementación de software y hardware: busque los coeficientes del filtro (teniendo en cuenta la forma de representación del número, profundidad de bits, etc.). Se introducen las definiciones de filtros FIR simétricos, la respuesta de fase lineal y su relación con el concepto de retraso grupal.

Funciones de ventana en tareas de filtrado

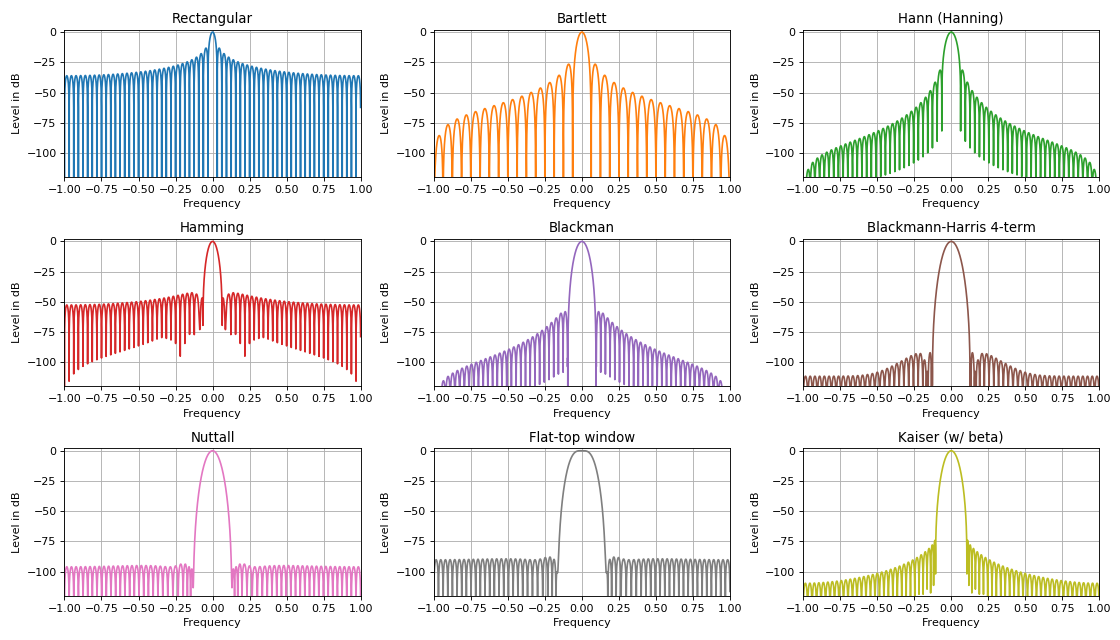
En las tareas de procesamiento de señal digital, se utilizan funciones de ventana de varias formas que, cuando se superponen a una señal en el dominio del tiempo, pueden mejorar cualitativamente sus características espectrales. Una gran cantidad de varias ventanas se debe principalmente a una de las características principales de cualquier superposición de ventanas. Esta característica se expresa en la relación entre el nivel de los lóbulos laterales y el ancho del lóbulo central. Regla:

Cuanto más fuerte es la supresión de los lóbulos laterales del espectro, más ancho es el lóbulo principal del espectro y viceversa.

Una de las aplicaciones de las funciones de ventana: detección de señales débiles en el contexto de las más fuertes al suprimir el nivel de los lóbulos laterales. Las funciones de la ventana principal en las tareas de DSP son ** triangular, sinusoidal, Lanczos, Hann, Hamming, Blackman, Harris, ventana Blackman-Harris, ventana plana, ventana Natall, Gauss, Kaiser ** y muchas otras. La mayoría de ellos se expresan a través de una serie finita sumando señales armónicas con pesos específicos. Dichas señales se implementan perfectamente en la práctica en cualquier dispositivo de hardware (circuitos lógicos programables o procesadores de señal).

Muestreo Decimación e interpolación

En esta sección se analizan los problemas del procesamiento de señales de varias velocidades: cambios en la frecuencia de muestreo. El procesamiento de señales a múltiples velocidades (procesamiento de múltiples velocidades) sugiere que en el proceso de conversión lineal de señales digitales, es posible cambiar la frecuencia de muestreo en la dirección de disminución o aumento, o en un número fraccionario de veces. Esto conduce a un procesamiento de señal más eficiente, ya que abre la posibilidad de utilizar las frecuencias de muestreo mínimas permitidas y, como resultado, una reducción significativa en el rendimiento informático requerido del sistema digital diseñado.

Decimación (decimación): disminución de la resolución. Interpolación : aumento de la frecuencia de muestreo.

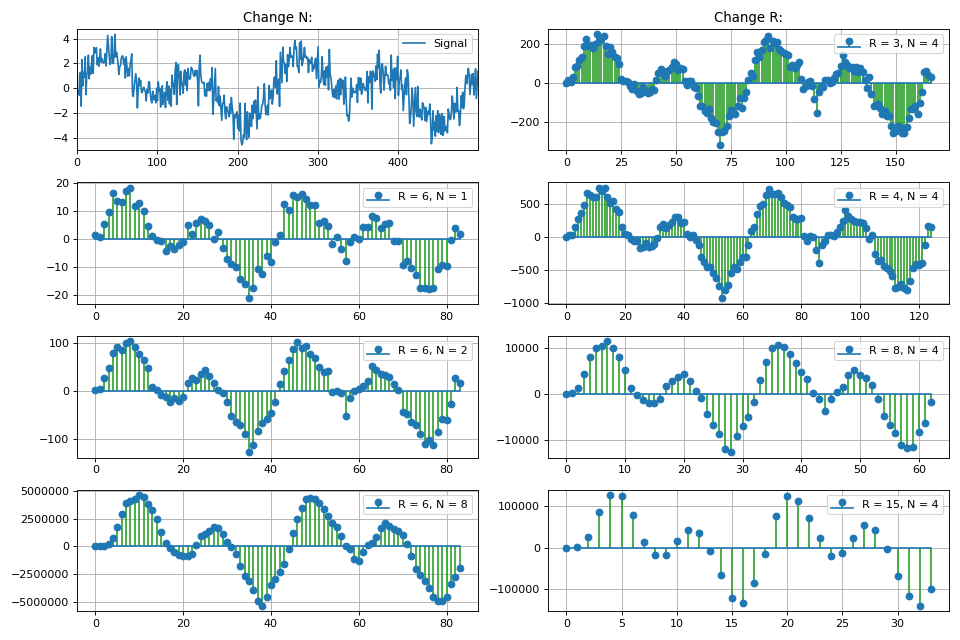
La sección también considera la clase de filtros FIR homogéneos, que se denominan filtros de peine integral (CIC, integrador en cascada - peine). Se muestran la implementación, las propiedades básicas y las características de los filtros CIC. Debido a la linealidad de las operaciones matemáticas que ocurren en el filtro CIC, es posible conectar en cascada varios filtros en una fila, lo que da una disminución proporcional en el nivel de los lóbulos laterales, pero también aumenta el "bloqueo" del lóbulo principal de la característica de amplitud-frecuencia.



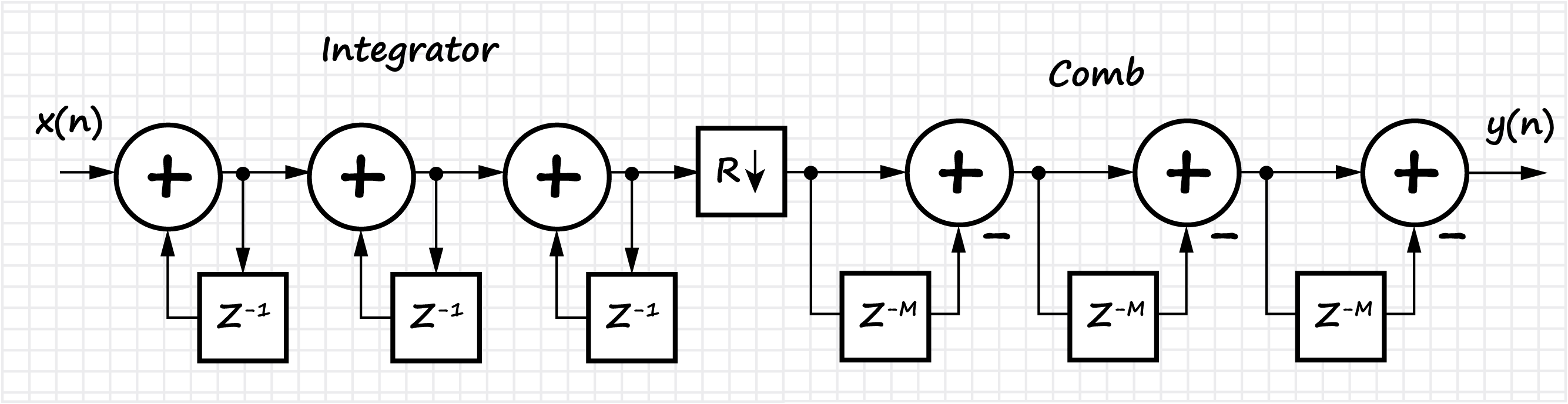
Gráfico de la respuesta de frecuencia del filtro según el coeficiente de diezmado:



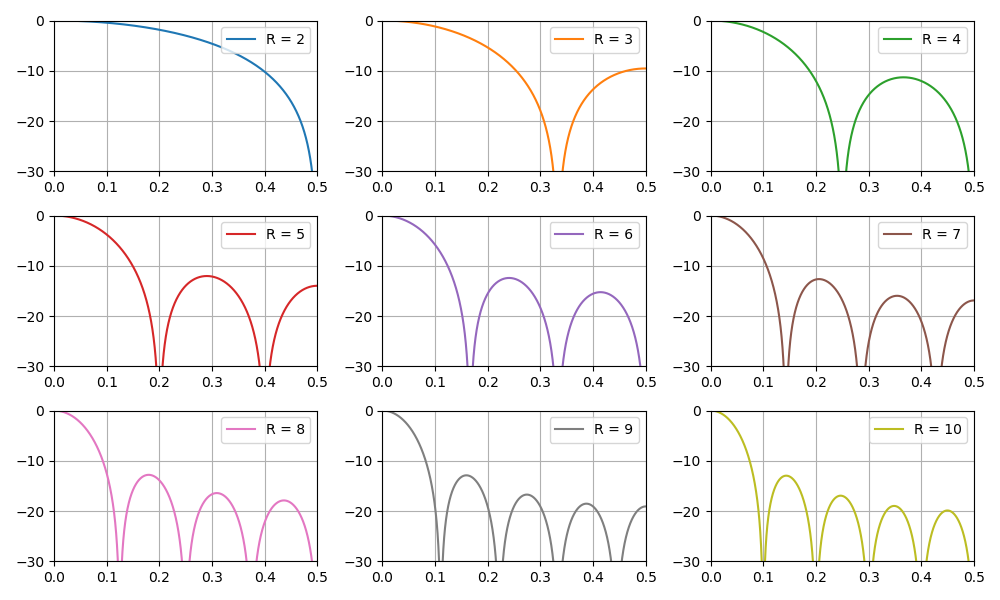
También en esta sección discutimos el problema de aumentar la profundidad de bits de los datos en la salida del filtro CIC, dependiendo de sus parámetros. Esto es especialmente importante en las tareas de implementación de software, en particular en FPGA.

Para la implementación práctica de filtros CIC en Python, se ha desarrollado una clase separada CicFilter que implementa métodos de diezmado e interpolación. También se muestran cambios en la frecuencia de muestreo utilizando los métodos integrados del paquete scipy Python.





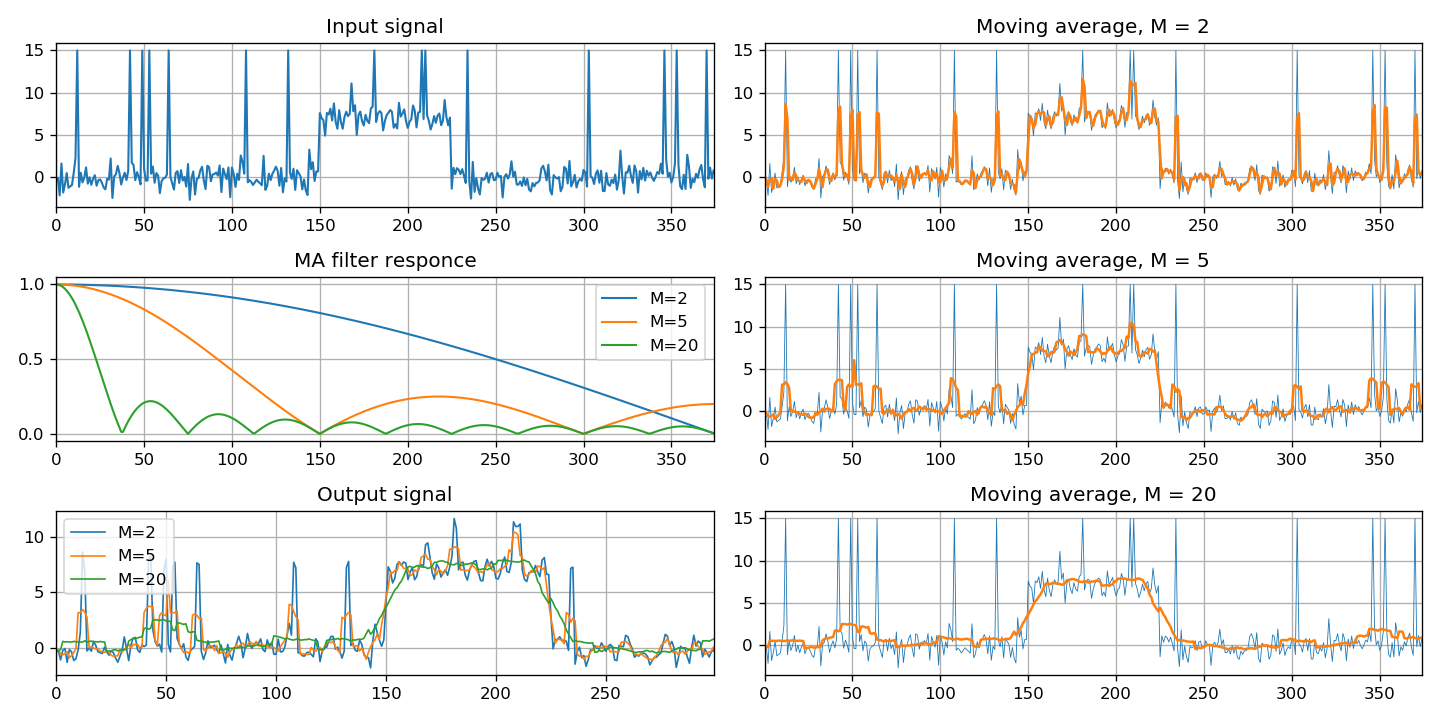
Finalmente, esta sección proporciona una clase especial de filtros: el promedio móvil. Se muestran tres métodos de implementación: mediante convolución de señales, utilizando un filtro FIR y un filtro IIR.

Conclusión

Espero que este curso en conjunto con mis artículos anteriores sobre el procesamiento digital de señales FPGA brinde beneficios prácticos y ayude al lector a comprender mejor los conceptos básicos del procesamiento digital de señales. Este proyecto será mejorado y complementado con nuevo material útil y no menos interesante. Sigue el desarrollo!

Además de este material, apoyo y desarrollo mi proyecto en los principales módulos DSP (en Python). Contiene un paquete para generar varias señales, una clase de filtros CIC para problemas de decimación e interpolación, un algoritmo para calcular los coeficientes de un filtro FIR corrector, un filtro de promedio móvil, un algoritmo para calcular una FFT ultra larga a través de métodos de conversión bidimensionales (este último fue muy útil cuando se trabajaba con implementación de hardware en FPGA) .

Gracias por su atencion!