En la escuela, tuve un compañero de clase que podía escuchar cómo funciona el automóvil en el patio, y con una cara seria emitir un veredicto: ¡todo está en orden o algo se ha roto, y necesito urgentemente correr por nuevas piezas / aceite / herramientas! Yo, como una tetera absoluta en el negocio automotriz, siempre escuché el ruido habitual del próximo dvenashka, sin notar ninguna diferencia y simplemente maravillándome silenciosamente de su audición y habilidades.
Ahora no entendía mejor el interior del automóvil, pero comencé a trabajar con el procesamiento de señales de sonido y el aprendizaje automático, y aquí intentaremos comprender si es posible enseñarle a una computadora a detectar anomalías en el sonido de un motor.
Como mínimo, es interesante comprobarlo y, en el futuro, dicha tecnología podría ahorrar mucho dinero para los propietarios de automóviles. Al menos en mi opinión, las fallas críticas ocurren gradualmente bajo el capó, y en las primeras etapas, muchas de ellas pueden escucharse, repararse rápida y económicamente, ahorrando tiempo, dinero y nervios ya temblorosos.
Bueno, tal vez es hora de pasar de las palabras a los hechos. Vamos!
Quiero decir de inmediato que en todo lo que concierne a las matemáticas y los algoritmos, pondré más énfasis en el significado y la comprensión, aquí no habrá fórmulas ni cálculos matemáticos. No he desarrollado ningún algoritmo nuevo aquí; para las fórmulas, si lo desea, es mejor google y Wikipedia, así como utilizar los enlaces que dejaré a lo largo del artículo.
Daré todas las explicaciones sobre el ejemplo del sonido de un motor averiado tomado de este video en YouTube .
El archivo descargado de YouTube (puede descargarlo usando extensiones del navegador o simplemente cambiando el enlace de YouTube a ssyoutube) lo convertimos al formato wav usando ffmpeg:
ffmpeg -i input_video.mp4 -c:a pcm_s16le -ar 16000 -ac 1 engine_sound.wav
Antes de comenzar a procesar este archivo, diré algunas palabras sobre qué es un espectrograma y cómo nos será útil para resolver este problema. Muchos de ustedes, sin duda, han visto una imagen similar: esta es la representación de amplitud temporal del sonido o un oscilograma.
Si en términos simples, entonces el sonido es una onda, y los valores de amplitud de esta onda se observan en el oscilograma en momentos determinados.
Para obtener un espectrograma de tal representación, necesitamos la transformada de Fourier. Con su ayuda, puede obtener la representación de amplitud-frecuencia del sonido o el espectro de amplitud. Tal espectro muestra a qué frecuencia y con qué amplitud se expresa la señal en estudio.
De hecho, un espectrograma es un conjunto de espectros de piezas cortas consecutivas de una señal. Quizás tal "definición" será suficiente para que no nos distraigamos mucho de la tarea. Todo se volverá más claro si observa la visualización del espectrograma (la imagen se obtuvo con WaveAssistant ). El tiempo se representa en el eje X, la frecuencia en el eje Y, es decir, cada columna en esta matriz es el módulo del espectro en un punto dado en el tiempo.
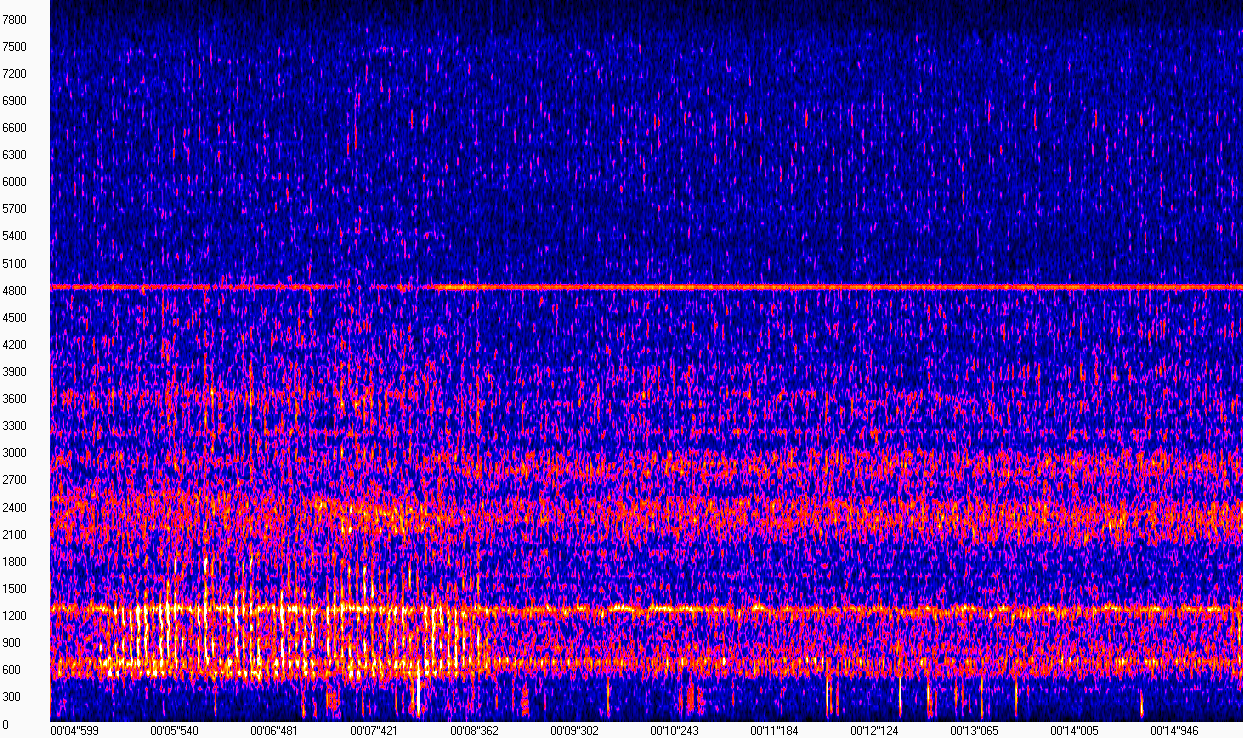
Este espectrograma muestra que el sonido del motor en ausencia de golpeteo "se ve" casi igual, y se expresa en frecuencias cercanas a 600, 1200, 2400 y 4800 Hz. El sonido de un golpe que molesta al propietario es muy distinto en el rango de frecuencia de 600-1200 Hz de 5 a 8 segundos. Dado que la grabación se realizó en condiciones bastante ruidosas en la calle, estos ruidos también están presentes en el espectrograma, lo que complica un poco nuestra tarea.
Sin embargo, al observar tal espectrograma, podemos decir con confianza dónde fue el golpe y dónde no. La computadora no tiene ojos, por lo tanto, debemos seleccionar un algoritmo que pueda distinguir entre dicha desviación (y preferiblemente no solo), sujeto a la presencia de ruido en la grabación.
Los espectrogramas se pueden calcular utilizando la biblioteca de librosa de la siguiente manera:
from librosa.util import buf_to_float from librosa.core import stft
Solución
Estrictamente hablando, necesitamos resolver el problema de clasificación binaria, donde necesitamos determinar si el motor está roto o está funcionando normalmente. Mi colega y yo ya describimos tareas similares en nuestro artículo anterior , donde utilizamos una red neuronal convolucional para clasificar eventos acústicos. Aquí, tal solución es casi imposible: las neuronas son muy aficionadas cuando reciben grandes conjuntos de datos. Estamos lidiando con una sola sangría que dura un poco más de un minuto, que obviamente no puede llamarse un gran conjunto de datos.
La elección se detuvo en el modelo de mezcla gaussiana (modelo de mezclas gaussianas). Aquí se puede encontrar un buen artículo que detalla el principio de operación y capacitación de este modelo . La idea general de este modelo es describir los datos utilizando una distribución compleja en forma de una combinación lineal de varias distribuciones normales multidimensionales (más sobre la distribución normal multidimensional aquí ).
Dado que el motor durante su funcionamiento suena aproximadamente "igual", el sonido de su funcionamiento puede considerarse estacionario, y la idea de describir este sonido utilizando dicha distribución parece bastante significativa. Para comprender la esencia de GMM, recomiendo mirar un ejemplo de entrenamiento y elegir la cantidad de gaussoides aquí .
Nuestro caso difiere de los ejemplos anteriores en que, en lugar de puntos en un plano bidimensional, se utilizarán los valores del espectro tomados del espectrograma de la señal. Puede seleccionar parámetros de distribución, como el tipo de matriz de covarianza utilizando el criterio BIC ( ejemplo , descripción ), sin embargo, en mi caso, los parámetros óptimos desde el punto de vista de este criterio se mostraron peores que los que se muestran en el siguiente código:
from sklearn.mixture import GaussianMixture n_components = 3 gmm_clf = GaussianMixture(n_components) gmm_clf.fit(X_train)
Suponiendo que el sonido del funcionamiento normal se describe mediante una distribución, cuyos parámetros se seleccionaron durante el proceso de entrenamiento, es posible medir qué tan cerca está cualquier sonido de esta distribución.
Para hacer esto, puede calcular la probabilidad promedio de las columnas del espectrograma de la señal estudiada, y luego elegir un umbral que separe la probabilidad de sonidos de buen trabajo de todos los demás. La credibilidad para cada segundo es la siguiente:
n_seconds = len(full_wav_data) // sr gmm_scores = []
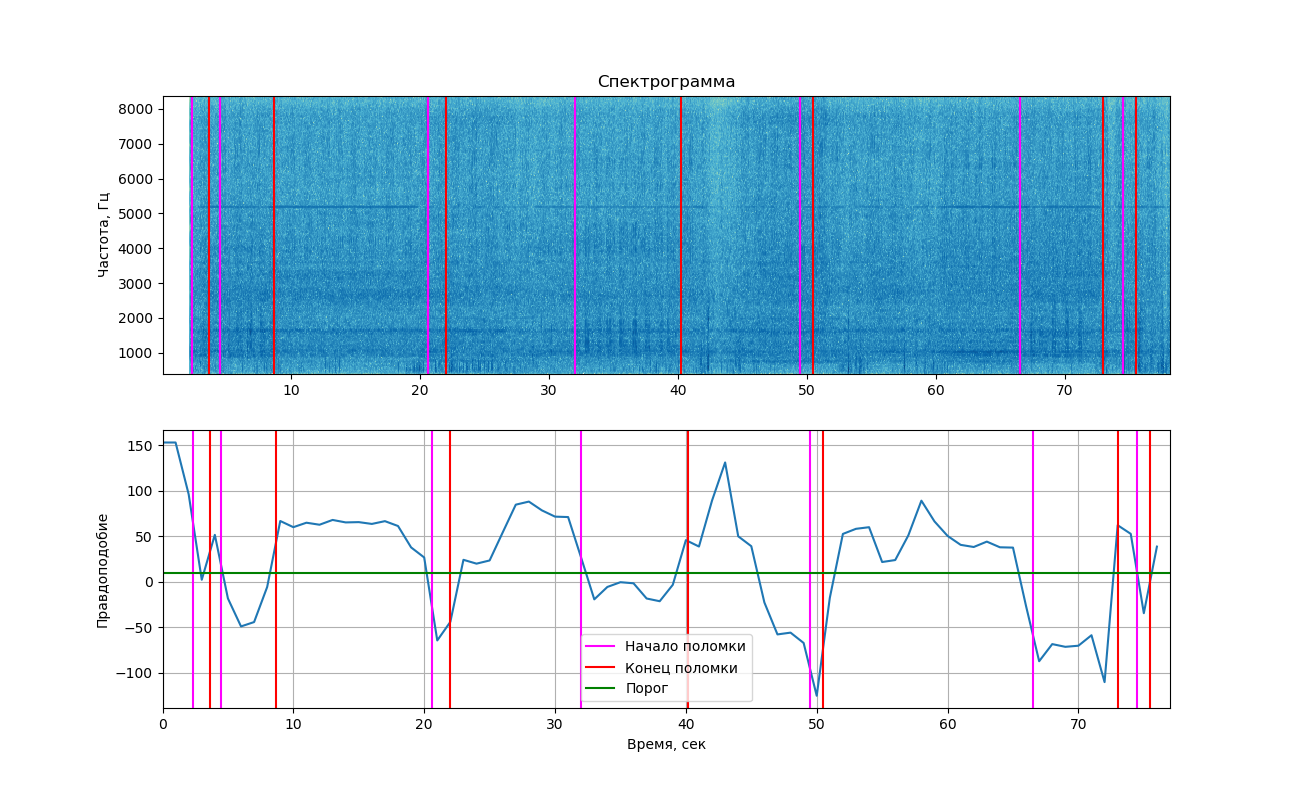
Si muestra la probabilidad obtenida en el gráfico, obtenemos la siguiente imagen.
La parte superior muestra el espectrograma de la señal que se muestra usando la biblioteca matplotlib. Los cambios causados por los golpes no se notan tanto como en el ejemplo anterior (por lo que viste 2 imágenes aquí). Sin embargo, si miras de cerca, todavía se pueden ver. Las líneas verticales marcan los tiempos de inicio y finalización de los golpes.
Conclusiones
Como puede ver en el gráfico, en el momento del sonido de un golpe, la probabilidad realmente cayó por debajo del umbral, lo que significa que podríamos separar estas dos clases (trabajando con y sin golpe). Pero debo decir que este valor está lo suficientemente cerca del umbral y en áreas donde no se escucha el golpe. Esto se debe a que a menudo se encuentra ruido extraño en la grabación, lo que también afecta la probabilidad.
Agregamos aquí entrenamiento en solo unos segundos de sonido, malas condiciones de grabación, ¡y ya puede sorprenderse de que el experimento haya tenido algún éxito!
Lo más probable es que para poner en práctica este método y estar seguro de su fiabilidad, tendrá que grabar mucho más sonido y también colocar bien el micrófono para minimizar el ruido que entra en las grabaciones.
Este artículo es solo un intento de resolver un problema similar, sin reclamar una corrección absoluta, si tiene ideas y sugerencias, o tal vez preguntas, hablemos juntos en los comentarios o en persona.
El código completo de github está aquí