Se preparó la traducción del artículo para los estudiantes del curso "Matemáticas para la ciencia de datos"

Anotación

Este artículo analiza la tarea de encontrar contornos faciales para una sola imagen. Mostramos cómo se puede usar el conjunto de árboles de regresión para predecir la posición de los contornos faciales directamente desde un subconjunto disperso de intensidades de píxeles, logrando un superrendimiento en tiempo real con predicciones de alta calidad. Presentamos una estructura general basada en el aumento de gradiente para estudiar un conjunto de árboles de regresión que optimiza la suma de las pérdidas cuadráticas y, naturalmente, procesa datos faltantes o parcialmente etiquetados. Mostraremos cómo el uso de distribuciones apropiadas que tienen en cuenta la estructura de los datos de la imagen ayuda en la selección eficiente de contornos. También se están investigando diversas estrategias de regularización y su importancia en la lucha contra el reciclaje. Además, analizamos el efecto de la cantidad de datos de entrenamiento sobre la precisión de los pronósticos y examinamos el efecto de aumentar los datos utilizando datos sintetizados.

1. Introducción

En este artículo, presentamos un nuevo algoritmo que busca contornos faciales en milisegundos y logra una precisión superior o comparable a los métodos modernos en conjuntos de datos estándar. El aumento de la velocidad en comparación con los métodos anteriores es una consecuencia de la identificación de los componentes principales de los algoritmos anteriores para la búsqueda de contornos faciales y su posterior inclusión en una forma optimizada en la cascada de modelos de regresión con gran ancho de banda, ajustados mediante el aumento de gradiente.

Demostramos, como ya lo hicimos antes [8, 2], que la búsqueda de contornos faciales se puede llevar a cabo utilizando una cascada de modelos de regresión. En nuestro caso, cada modelo de regresión en la cascada predice efectivamente la forma de la cara según el pronóstico inicial y la intensidad del escaso conjunto de píxeles indexados en relación con este pronóstico inicial. Nuestro trabajo se basa en una gran cantidad de estudios realizados durante la última década, que han llevado a un progreso significativo en la tarea de encontrar contornos faciales [9, 4, 13, 7, 15, 1, 16, 18, 3, 6, 19]. En particular, hemos incluido en nuestros modelos de regresión ajustados dos elementos clave que están presentes en varios de los algoritmos exitosos a continuación, y ahora detallamos estos elementos.

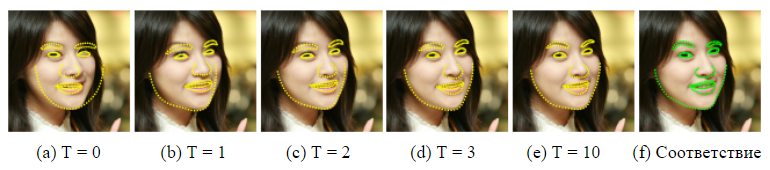
Figura 1. Resultados seleccionados en el conjunto de datos HELEN. Para detectar 194 puntos clave (puntos de referencia) en la cara en una imagen en un milisegundo, se utiliza un conjunto de árboles de regresión aleatoria.

El primero gira en torno a la indexación de la intensidad de píxeles en relación con el pronóstico actual de la forma de la cara. Las características distinguidas en la representación vectorial de la imagen de la cara pueden variar mucho debido a la deformación de la forma y debido a factores interferentes como los cambios en las condiciones de iluminación. Esto hace que sea difícil predecir con precisión la forma usando estas funciones. El dilema es que necesitamos signos confiables para predecir con precisión la forma y, por otro lado, necesitamos un pronóstico preciso de la forma para extraer signos confiables. En el trabajo anterior [4, 9, 5, 8], así como en este trabajo, se utiliza un enfoque iterativo (cascada) para resolver este problema. En lugar de retroceder los parámetros de forma en función de las características extraídas en el sistema de coordenadas de imagen global, la imagen se convierte en un sistema de coordenadas normalizado en función del pronóstico de forma actual, y luego se extraen signos para predecir el vector de actualización para los parámetros de forma. Este proceso generalmente se repite varias veces hasta la convergencia.

El segundo examina cómo lidiar con la complejidad del problema de explicación / predicción. Durante las pruebas, el algoritmo de búsqueda de contornos debe predecir la forma de la cara, un vector de alta dimensión que está en el mejor acuerdo con los datos de imagen y nuestro modelo de forma. El problema no es convexo con muchos óptimos locales. Los algoritmos exitosos [4, 9] resuelven este problema, suponiendo que la forma predicha debe estar en un subespacio lineal que puede detectarse, por ejemplo, al encontrar los componentes principales de las formas de entrenamiento. Esta suposición reduce significativamente el número de formas potenciales consideradas durante la explicación y puede ayudar a evitar los óptimos locales.

Un trabajo reciente [8, 11, 2] explota el hecho de que una cierta clase de regresores está garantizada para crear predicciones que se encuentran en el subespacio lineal definido por las formas de aprendizaje, y no hay necesidad de restricciones adicionales. Es importante que nuestros modelos de regresión tengan estos dos elementos.
Estos dos factores están asociados con nuestro entrenamiento efectivo en el modelo de regresión. Optimizamos la función de pérdida correspondiente y realizamos la selección de características en función de los datos. En particular, entrenamos a cada regresor usando el aumento de gradiente [10] usando la función de pérdida cuadrática, la misma función de pérdida que queremos minimizar durante la prueba. El conjunto de píxeles dispersos utilizados como entrada para el regresor se selecciona usando una combinación del algoritmo de aumento de gradiente y la probabilidad a priori de las distancias entre pares de píxeles de entrada. La distribución a priori permite que el algoritmo de refuerzo investigue eficientemente una gran cantidad de características relevantes. El resultado es una cascada de regresores que pueden localizar puntos de referencia faciales cuando se inicializan desde el frente.

Las principales contribuciones de este artículo son:

1. Un nuevo método para encontrar contornos faciales, basado en un conjunto de árboles de regresión (árboles de decisión), que realiza la selección de características invariantes de la forma, mientras minimiza la misma función de pérdida durante el entrenamiento que queremos minimizar durante las pruebas.
2. Presentamos una extensión natural de nuestro método que procesa etiquetas faltantes o indefinidas.
3. Se presentan resultados cuantitativos y cualitativos, que confirman que nuestro método ofrece pronósticos de alta calidad, siendo mucho más efectivo que el mejor método anterior (Figura 1).
4. Se analiza la influencia de la cantidad de datos de entrenamiento, el uso de datos parcialmente etiquetados y datos generalizados sobre la calidad de los pronósticos.

2. Método

Este artículo presenta un algoritmo para evaluar con precisión la posición de los puntos de referencia faciales (puntos clave) en términos de eficiencia computacional. Como en trabajos anteriores [8, 2], la cascada de regresores se utiliza en nuestro método. En el resto de esta sección, describimos los detalles de la forma de los componentes individuales de la cascada y cómo llevamos a cabo el entrenamiento.

2.1. Cascada de regresión

Primero presentamos alguna notación. Dejar , coordenadas y del hito número i de la cara en la imagen I. Luego el vector denota las coordenadas de todas las caras p en I. A menudo en este artículo llamamos al vector S una forma. Nosotros usamos para indicar nuestra calificación actual S. Cada regresor (·, ·) En la cascada predice el vector de actualización de la imagen y que se agrega a la evaluación del formulario actual Para mejorar la calificación:

) (1)

El punto clave de la cascada es que el regresor hace sus pronósticos basados ​​en atributos tales como intensidades de píxeles calculados por I e indexados en relación con la estimación de forma actual . Esto introduce algún tipo de invariancia geométrica en el proceso, y a medida que avanza por la cascada, puede estar más seguro de que la ubicación semántica exacta en la cara está indexada. Más adelante describiremos cómo se realiza esta indexación.

Tenga en cuenta que el rango de salida extendido por el conjunto está garantizado en el subespacio lineal de los datos de entrenamiento si la estimación inicial Pertenece a este espacio. Por lo tanto, no necesitamos introducir restricciones adicionales en las predicciones, lo que simplifica enormemente nuestro método. La forma inicial se puede seleccionar simplemente como la forma intermedia de datos de entrenamiento, centrada y escalada de acuerdo con la salida del cuadro delimitador del detector de cara general.

Educar a todos Utilizamos el algoritmo de aumento de gradiente para árboles con la suma de pérdidas cuadráticas, como se describe en [10]. Ahora daremos detalles detallados de este proceso.

2.2. Entrenando a cada regresor en una cascada

Supongamos que tenemos datos de entrenamiento donde todos es una imagen de la cara, y Su vector de forma. Para descubrir la primera función de regresión en la cascada, creamos a partir de nuestros tripletes de datos de entrenamiento de la imagen de la cara, el pronóstico de forma inicial y el paso de actualización del objetivo, es decir ) donde

(2)

(3) y

(4)

para i = 1, ..., N.

Establecemos el número total de estos tripletes en N = nR, donde R es el número de inicializaciones utilizadas en la imagen Ii. Cada pronóstico de forma inicial para la imagen se selecciona uniformemente de Sin reemplazo.

Sobre estos datos entrenamos la función de regresión (ver Algoritmo 1) usando el aumento gradual de los árboles con la suma de las pérdidas cuadráticas. El conjunto de triplete de entrenamiento se actualiza para proporcionar datos de entrenamiento. % 20) para el siguiente regresor en la cascada configurando (con t = 0).

% 20) (5)

(6)

Este proceso se repite hasta que se entrena una cascada de regresores T. que en combinación proporcionan un nivel suficiente de precisión.

Como se indica, cada regresor aprende usando el algoritmo de impulso del árbol de gradiente. Debe recordarse que se utiliza la función de pérdida cuadrática, y los residuos calculados en el bucle interno corresponden al gradiente de esta función de pérdida estimado en cada muestra de entrenamiento. La formulación del algoritmo incluye el parámetro de velocidad de aprendizaje 0 <ν ≤ 1, también conocido como coeficiente de regularización. Establecer ν <1 ayuda a combatir la reconfiguración y generalmente conduce a regresores que generalizan mucho mejor que aquellos entrenados con ν = 1 [10].

Algoritmo de aprendizaje 1 en cascada

Tenemos datos de entrenamiento y tasa de aprendizaje (coeficiente de regularización) 0 <ν <1

1. Inicializar
   
2. para k = 1, ..., K:
   a) establecemos para i = 1, ...,
   
   b) Ajustamos el árbol de regresión al objetivo con función de regresión débil .
   c) Actualización
3. Conclusión
   

2.3. Árbol regresor

En el núcleo de cada función de regresión rt hay regresores en forma de árbol adecuados para objetivos residuales durante el algoritmo de aumento de gradiente. Ahora veremos los detalles de implementación más importantes para entrenar cada árbol de regresión.

2.3.1 Pruebas de forma dividida invariable

En cada nodo de separación en el árbol de regresión, tomamos una decisión basada en el valor umbral de la diferencia entre las intensidades de dos píxeles. Los píxeles utilizados en la prueba están en las posiciones u y v cuando se definen en el sistema de coordenadas de forma intermedia. Para una imagen de una cara con una forma arbitraria, nos gustaría indexar puntos que tienen la misma posición con respecto a su forma que u y v, para la forma promedio. Para hacer esto, antes de extraer los elementos, la imagen se puede deformar a la forma media en función de la estimación de forma actual. Dado que usamos solo una representación muy escasa de la imagen, es mucho más eficiente deformar la disposición de los puntos que toda la imagen. Además, se puede hacer una aproximación aproximada de la deformación utilizando solo la transformación de similitud global además de los desplazamientos locales, como se propone en [2].

Los detalles exactos son los siguientes. Dejar Es el índice del punto de referencia en la cara en la forma media más cercano a usted, y define su desplazamiento desde u como .

Luego para la forma Si definida en la imagen posición en , que es cualitativamente similar a u en la imagen de una forma mediana, se define como
(7)

donde y - matriz de escala y rotación de la transformación de similitud que transforma en , forma media

Escala y rotación minimizan

(8)

la suma de los cuadrados entre los puntos de referencia de la forma media, y punto de urdimbre. definido de manera similar.

Formalmente, cada división es una solución que incluye 3 parámetros θ = (τ, u, v), y se aplica a cada ejemplo de entrenamiento y prueba como

(9)

donde y se determinan utilizando la matriz de escala y rotación que mejor se deforma en de acuerdo con la ecuación (7). En la práctica, las tareas y los desplazamientos locales se determinan en la etapa de capacitación. El cálculo de la transformación de similitud, durante la prueba de la parte más cara de este proceso, se realiza solo una vez en cada nivel de la cascada.

2.3.2 Selección de particiones nodales

Para cada árbol de regresión, aproximamos la función básica por una función lineal por partes, donde un vector constante es adecuado para cada nodo finito. Para entrenar el árbol de regresión, generamos aleatoriamente un conjunto de particiones adecuadas, es decir, θ, en cada nodo. Luego seleccionamos ansiosamente θ * de estos candidatos, lo que minimiza la suma del error cuadrático. Si Q es un conjunto de índices de ejemplos de entrenamiento en un nodo, esto corresponde a la minimización

(10)

donde - índices de ejemplos que se envían al nodo izquierdo debido a la decisión θ, Es el vector de todos los residuos calculados para la imagen i en el algoritmo de aumento de gradiente, y

para (11)

La partición óptima se puede encontrar de manera muy eficiente, porque si transformamos la ecuación (10) y omitimos factores independientes de θ, podemos ver que

Aquí solo necesitamos calcular al evaluar varios θ, ya que se puede calcular a partir de los objetivos promedio en el nodo principal µ y como sigue:

2.3.3 Selección de características

La solución en cada nodo se basa en un valor umbral de la diferencia en los valores de intensidad en un par de píxeles. Esta es una prueba bastante simple, pero es mucho más efectiva que un valor umbral con una sola intensidad, debido a su relativa insensibilidad a los cambios en la iluminación global. Desafortunadamente, la desventaja de usar diferencias de píxeles es que el número de candidatos potenciales de separación (característica) es cuadrático con respecto al número de píxeles en la imagen promedio. Esto hace que sea difícil encontrar buenos θ sin buscar una gran cantidad de ellos. Sin embargo, este factor limitante puede debilitarse un poco, teniendo en cuenta la estructura de los datos de la imagen.

Introducimos la distribución exponencial

(12)

por la distancia entre los píxeles utilizados en la división para fomentar la selección de pares de píxeles más cercanos.

Hemos descubierto que el uso de esta distribución simple reduce el error de predicción para varios conjuntos de datos faciales. La Figura 4 compara las características seleccionadas con y sin ella, donde el tamaño del grupo de objetos en ambos casos se establece en 20.

2.4. Manejo de etiquetas faltantes

El problema de la ecuación (10) puede extenderse fácilmente para manejar el caso cuando algunos puntos de referencia no están marcados en algunas imágenes de entrenamiento (o tenemos una medida de incertidumbre para cada punto de referencia). Introducir variable [0, 1] para cada imagen de entrenamiento i y cada punto de referencia j . Instalación un valor de 0 indica que el hito j no está marcado en la i- ésima imagen, y un ajuste de 1 indica que está marcado. Entonces la ecuación (10) se puede representar de la siguiente manera

donde - matriz diagonal con vector en su diagonal y

para (13)

El algoritmo de aumento de gradiente también debe modificarse para tener en cuenta estos pesos. Esto se puede hacer simplemente inicializando el modelo de conjunto con el valor promedio ponderado de los objetivos y ajustando los árboles de regresión a los residuos ponderados en el algoritmo 1 de la siguiente manera

(14)

3. Experimentos

Bases: para evaluar con precisión el rendimiento de nuestro método propuesto, conjunto de árboles de regresión (ERT), creamos dos bases más. El primero se basa en helechos aleatorios (helechos aleatorios) con una selección aleatoria de rasgos (EF), y el otro es una versión más avanzada de este enfoque con la selección de rasgos basados ​​en la correlación (EF + CB), que es nuestra nueva implementación [2]. Todos los parámetros son fijos para los tres enfoques.

EF utiliza la implementación directa de helechos aleatorios como regresores débiles en el conjunto y es el más rápido para el entrenamiento. Utilizamos el mismo método de regularización que se sugiere en [2] para la regularización de helechos.

EF + CB utiliza un método de selección de objetos basado en correlación que proyecta valores de salida, 's, en una dirección aleatoria w y selecciona pares de signos (u, v) para los cuales tiene la mayor correlación de muestra para los datos de entrenamiento con objetivos predichos .

Parámetros
A menos que se especifique lo contrario, todos los experimentos se realizan con las siguientes configuraciones de parámetros fijos. El número de regresores fuertes rt en la cascada es T = 10, y cada uno consiste en K = 500 regresores débiles . Profundidad de los árboles (o helechos) utilizados para representar , establecido igual a F = 5. En cada nivel de la cascada, P = 400 píxeles se seleccionan de la imagen. Para entrenar regresores débiles, seleccionamos aleatoriamente un par de estos píxeles P de acuerdo con nuestra distribución y seleccionamos un umbral aleatorio para crear una separación potencial, como se describe en la ecuación (9). La mejor separación se logra repitiendo este proceso S = 20 veces y eligiendo el que optimice nuestro objetivo. , R = 20 .

2. , Viola & Jones [17]. .

O (TKF). O (NDTKF S), N — , D — . HELEN [12], .

, , HELEN [12], , , . 2330 , 194 . 2000 , .

LFPW [1], 1432 . , 778 216 , , .

Comparación
1 . (Active Shape Models) — STASM [14] CompASM [12].

1. HELEN. — . . , . , . .

, , . 3 , , ERT , . , EF + CB . , EF + CB , .

LFPW [1] ( 2). EF + CB , [2]. ( , .) , , .

2. LFPW. 1.

4 (12) , , . λ 0,1 . . 4 .

3. . , , . (12).

, . , . — . ν 1 ( ν = 0.1). . , , , ν = 1. (10 ) . ( .)

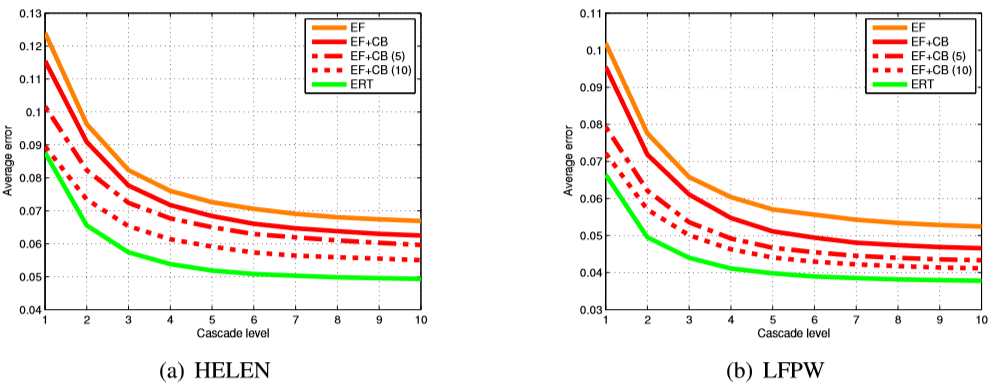
3. HELEN (a) LFPW (b). EF — , EF + CB — , . (5 10), [2]. , (ERT), , , .

4. , . , .

, . , .

4. HELEN . .

, . , , , , .

. . 5 . , , [8, 2] ( 10 × 400 .)

5. .

Datos de entrenamiento
Para probar la efectividad de nuestro método en términos del número de imágenes de entrenamiento, entrenamos varios modelos de diferentes subconjuntos de datos de entrenamiento. La Tabla 6 resume los resultados finales, y la Figura 5 muestra un gráfico de errores en cada nivel de la cascada. Usar muchos niveles de regresores es más útil cuando tenemos una gran cantidad de ejemplos de entrenamiento.

Repetimos los mismos experimentos con un número total fijo de ejemplos extendidos, pero cambiamos la combinación de las formas iniciales usadas para crear el ejemplo de entrenamiento a partir de un ejemplo marcado de la cara y una cantidad de imágenes anotadas usadas para estudiar la cascada (Tabla 7).

Tabla 6. La tasa de error final para el número de ejemplos de entrenamiento. Al crear datos de entrenamiento para estudiar regresores en cascada, cada imagen de rostro etiquetada generaba 20 ejemplos de entrenamiento, utilizando 20 caras etiquetadas diferentes como una suposición inicial sobre la forma del rostro.

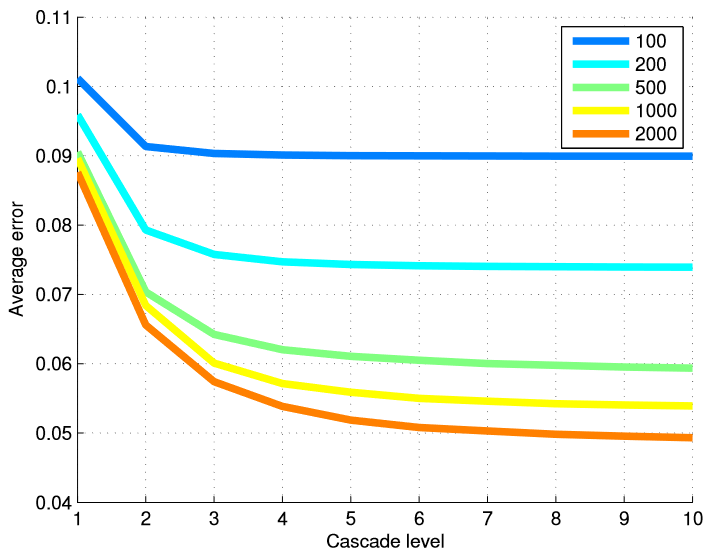
Figura 5. El error promedio en cada nivel de la cascada se presenta dependiendo del número de ejemplos de entrenamiento utilizados. El uso de muchos niveles de regresores es más útil cuando el número de ejemplos de entrenamiento es grande.

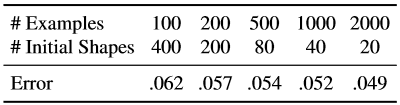
Tabla 7. Aquí el número efectivo de ejemplos de entrenamiento es fijo, pero usamos varias combinaciones del número de imágenes de entrenamiento y el número de formas iniciales usadas para cada imagen de rostro marcada.

El aumento de los datos de entrenamiento usando una variedad de formas iniciales expande el conjunto de datos en términos de forma. Nuestros resultados muestran que este tipo de suplemento no compensa completamente la ausencia de imágenes de entrenamiento anotadas. Aunque la tasa de mejora obtenida al aumentar el número de imágenes de entrenamiento está disminuyendo rápidamente después de los primeros cientos de imágenes.

Anotaciones parciales
La Tabla 8 muestra los resultados del uso de datos parcialmente anotados. 200 estudios de casos están anotados completamente, y el resto solo parcialmente.

Tabla 8. Resultados usando datos parcialmente etiquetados. 200 ejemplos siempre están completamente anotados. Los valores entre paréntesis indican el porcentaje de puntos de referencia observados.

Los resultados muestran que podemos lograr una mejora significativa utilizando datos parcialmente etiquetados. Sin embargo, la mejora mostrada puede no estar saturada, porque sabemos que el tamaño base de los parámetros de forma es mucho más bajo que el tamaño de los puntos de referencia (194 × 2). En consecuencia, existe la posibilidad de una mejora más significativa con las marcas parciales, si utiliza explícitamente la correlación entre la posición de los puntos de referencia. Tenga en cuenta que el procedimiento de aumento de gradiente descrito en este artículo no utiliza correlación entre puntos de referencia. Este problema puede resolverse en futuros trabajos.

4. Conclusión

Describimos cómo se puede usar un conjunto de árboles de regresión para hacer retroceder la ubicación de puntos de referencia faciales a partir de un subconjunto disperso de valores de intensidad extraídos de la imagen de entrada. La estructura presentada reduce el error más rápido que el trabajo anterior y también puede procesar marcas parciales o indefinidas. Si bien los componentes principales de nuestro algoritmo consideran diversas mediciones objetivo como variables independientes, la continuación natural de este trabajo será el uso de la correlación de los parámetros de forma para un entrenamiento más efectivo y un mejor uso de etiquetas parciales.

Figura 6. Resultados finales en la base de datos HELEN.

Agradecimientos
Este trabajo fue financiado por la Fundación Sueca de Investigación Estratégica como parte del proyecto VINST.

Literatura usada

[1] PN Belhumeur, DW Jacobs, DJ Kriegman y N. Kumar. Localización de partes de rostros utilizando un consenso de ejemplares. En CVPR, páginas 545–552, 2011. 1, 5
[2] X. Cao, Y. Wei, F. Wen y J. Sun. Alineación de caras por regresión explícita de formas. En CVPR, páginas 2887–2894, 2012. 1, 2, 3, 4, 5, 6
[3] TF Cootes, M. Ionita, C. Lindner y P. Sauer. Ajuste de modelo de forma robusto y preciso mediante votación de regresión forestal aleatoria. En ECCV, 2012.1
[4] TF Cootes, CJ Taylor, DH Cooper y J. Graham. Modelos de forma activa: su entrenamiento y aplicación. Visión por computadora y comprensión de imágenes, 61 (1): 38–59, 1995.1, 2
[5] D. Cristinacce y TF Cootes. Regresión activada modelos de forma activa. En BMVC, páginas 79.1–79.10, 2007.1
[6] M. Dantone, J. Gall, G. Fanelli y LV Gool. Detección de características faciales en tiempo real utilizando bosques de regresión condicional. En CVPR, 2012.1
[7] L. Ding y AM Martínez. Detección detallada precisa de rostros y rasgos faciales. En CVPR, 2008.1
[8] P. Dollar, P. Welinder y P. Perona. Regresión de pose en cascada. En CVPR, páginas 1078–1085, 2010. 1, 2, 6
[9] GJ Edwards, TF Cootes y CJ Taylor. Avances en modelos de apariencia activa. En ICCV, páginas 137–142, 1999. 1, 2
[10] T. Hastie, R. Tibshirani y JH Friedman. Los elementos del aprendizaje estadístico: minería de datos, inferencia y predicción. Nueva York: Springer-Verlag, 2001,2,3
[11] V. Kazemi y J. Sullivan. Alineación de caras con modelado basado en piezas. En BMVC, páginas 27.1–27.10, 2011.2
[12] V. Le, J. Brandt, Z. Lin, LD Bourdev y TS Huang. Localización interactiva de rasgos faciales. En [13] L. Liang, R. Xiao, F. Wen y J. Sun. Alineación de caras a través de búsqueda discriminativa basada en componentes. En ECCV, páginas 72–85, 2008. 1ECCV, páginas 679– 692, 2012.5
[14] S. Milborrow y F. Nicolls. Localización de rasgos faciales con un modelo de forma activa extendida. En ECCV, páginas 504–513, 2008.5
[15] J. Saragih, S. Lucey y J. Cohn. Ajuste del modelo deformable por medio de cambios medios regulares. Internation Journal of Computer Vision, 91: 200–215, 2010.1
[16] BM Smith y L. Zhang. Alineación de la cara conjunta con modelos de forma no paramétrica. En ECCV, páginas 43–56, 2012.1
[17] PA Viola y MJ Jones. Robusta detección de rostros en tiempo real. En ICCV, página 747, 2001.5
[18] X. Zhao, X. Chai y S. Shan. Alineación de la cara conjunta: Rescate las alineaciones malas con las buenas mediante un reajuste regular. En ECCV, 2012.1
[19] X. Zhu y D. Ramanan. Detección de rostros, estimación de posturas y localización de hitos en la naturaleza. En CVPR, páginas 2879–2886, 2012.1