¿Por qué el próximo artículo sobre cómo escribir redes neuronales desde cero? Por desgracia, no pude encontrar artículos donde la teoría y el código se describieran desde cero a un modelo totalmente funcional. Inmediatamente advierto que habrá muchas matemáticas. Supongo que el lector está familiarizado con los conceptos básicos de álgebra lineal, derivadas parciales y, al menos parcialmente, con la teoría de la probabilidad, así como con Python y Numpy. Nos ocuparemos de una red neuronal totalmente conectada y MNIST.
Matemáticas Parte 1 (simple)
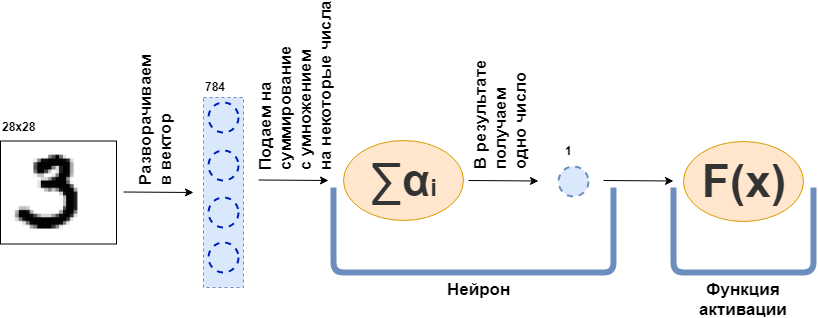
¿Qué es una capa totalmente conectada (capa FC)? Por lo general, dicen algo como "Una capa completamente conectada es una capa, cada neurona de la cual está conectada a todas las neuronas de la capa anterior". Simplemente no está claro qué son las neuronas, cómo están conectadas, especialmente en el código. Ahora intentaré analizar esto con un ejemplo. Que haya una capa de 100 neuronas. Sé que aún no he explicado de qué se trata, pero imaginemos que hay 100 neuronas y tienen una entrada a donde se envían los datos, y una salida desde donde dan los datos. Y una imagen en blanco y negro de 28x28 píxeles se alimenta a la entrada, solo 784 valores, si la estira en un vector. Una imagen se puede llamar una capa de entrada. Luego, para que cada una de las 100 neuronas se conecte con cada "neurona" o, si lo desea, el valor de la capa anterior (es decir, la imagen), es necesario que cada una de las 100 neuronas acepte 784 valores de la imagen original. Por ejemplo, para cada una de las 100 neuronas será suficiente multiplicar 784 valores de la imagen por unos 784 números y sumarlos, como resultado, sale un número. Es decir, esta es una neurona:
$$ display $$ \ text {Neuron output} = \ text {some number} _ {1} \ cdot \ text {picture value} _1 ~ + \\ + ~ ... ~ + ~ \ text {some- ese número} _ {784} \ cdot \ text {valor de imagen} _ {784} $$ display $$
Luego resulta que cada neurona tiene 784 números, y todos estos números: (número de neuronas en esta capa) x (número de neuronas en la capa anterior) =
$ en línea $ 100 \ times784 $ en línea $ = 78,400 dígitos. Estos números se denominan comúnmente pesos de capa. Cada neurona dará su número y como resultado obtenemos un vector de 100 dimensiones, y de hecho podemos escribir que este vector de 100 dimensiones se obtiene multiplicando el vector de 784 dimensiones (nuestra imagen original) por una matriz de peso de tamaño
$ en línea $ 100 \ times784 $ en línea $ :
$$ display $$ \ boldsymbol {x} ^ {100} = W_ {100 \ times784} \ cdot \ boldsymbol {x} ^ {784} $$ display $$
Además, los 100 números resultantes se transmiten a la función de activación, alguna función no lineal, que afecta a cada número por separado. Por ejemplo, sigmoide, tangente hiperbólica, ReLU y otros. La función de activación es necesariamente no lineal; de lo contrario, la red neuronal solo aprenderá transformaciones simples.
Luego, los datos resultantes se envían nuevamente a una capa totalmente conectada, pero con un número diferente de neuronas, y nuevamente a la función de activación. Esto pasa varias veces. La última capa de la red es la capa que produce la respuesta. En este caso, la respuesta es información sobre el número en la imagen.
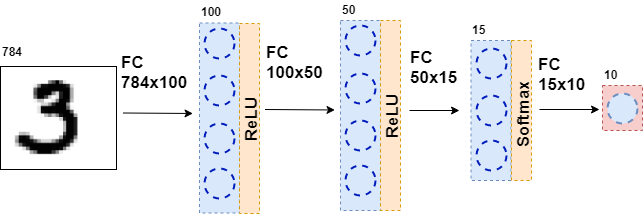
Durante el entrenamiento de la red, es necesario que sepamos qué figura se muestra en la imagen. Es decir, que el conjunto de datos está marcado. Entonces puede usar otro elemento: la función de error. Ella mira la respuesta de la red neuronal y la compara con la respuesta real. Gracias a esto, la red neuronal está aprendiendo.
Declaración general del problema.
El conjunto de datos completo es un tensor grande (llamaremos tensor a una matriz de datos multidimensional)
$ en línea $ \ boldsymbol {X} = \ left [\ boldsymbol {x} _1, \ boldsymbol {x} _2, \ ldots, \ boldsymbol {x} _n \ right] $ inline $ donde
$ en línea $ \ boldsymbol {x} _i $ en línea $ - i-ésimo objeto, por ejemplo, una imagen, que también es un tensor. Para cada objeto hay
$ en línea $ y_i $ en línea $ - la respuesta correcta en el i-ésimo objeto. En este caso, una red neuronal se puede representar como una función que toma un objeto como entrada y le da alguna respuesta:
$$ display $$ F (\ boldsymbol {x} _i) = \ hat {y} _i $$ display $$
Ahora echemos un vistazo más de cerca a la función
$ en línea $ F (\ boldsymbol {x} _i) $ en línea $ . Dado que la red neuronal consta de capas, cada capa individual es una función. Y eso significa
$$ display $$ F (\ boldsymbol {x} _i) = f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i)))) = \ hat {y} _i $$ display $ $ $
Es decir, en la primera función, la primera capa, se presenta una imagen en forma de algún tensor. Función
$ en línea $ f_1 $ en línea $ da alguna respuesta, también un tensor, pero de una dimensión diferente. Este tensor se llamará representación interna. Ahora esta representación interna se alimenta a la entrada de la función
$ en línea $ f_2 $ en línea $ , que da su representación interna. Y así sucesivamente, hasta que la función
$ en línea $ f_k $ en línea $ - última capa - no dará una respuesta
$ en línea $ \ hat {y} _i $ en línea $ .
Ahora, la tarea es capacitar a la red: hacer que la respuesta de la red coincida con la respuesta correcta. Primero debes medir qué tan equivocada está la red neuronal. Medir esto es una función de error.
$ en línea $ L (\ hat {y} _i, y_i) $ en línea $ . E imponemos restricciones:
1)
$ en línea $ \ hat {y} _i \ xrightarrow {} y_i \ Rightarrow L (\ hat {y} _i, y_i) \ xrightarrow {} 0 $ en línea $
2)
$ en línea $ \ existe ~ dL (\ hat {y} _i, y_i) $ en línea $
3)
$ en línea $ L (\ hat {y} _i, y_i) \ geq 0 $ en línea $
La restricción 2 se impone a todas las funciones de las capas.
$ en línea $ f_j $ en línea $ - Que todos sean diferenciables.
Además, de hecho (no mencioné esto) algunas de estas funciones dependen de los parámetros (los pesos de la red neuronal)
$ en línea $ f_j (\ boldsymbol {x} _i | \ boldsymbol {\ omega} _j) $ en línea $ . Y toda la idea es levantar esos pesos para que
$ en línea $ \ hat {y} _i $ en línea $ coincidió con
$ en línea $ y_i $ en línea $ en todos los objetos de un conjunto de datos. Observo que no todas las funciones tienen pesos.
Entonces, ¿dónde nos detuvimos? Todas las funciones de la red neuronal son diferenciables, la función de error también es diferenciable. Recuerde una de las propiedades del gradiente: muestre la dirección de crecimiento de la función. Usamos esto, restricciones 1 y 3, el hecho de que
$$ display $$ L (F (\ boldsymbol {x} _i)) = L (f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i)))))) L (\ hat {y} _i) $$ display $$
y el hecho de que puedo considerar derivadas parciales y derivadas de una función compleja. Ahora hay todo lo que necesitas para calcular
$$ display $$ \ frac {\ partial L (F (\ boldsymbol {x} _i))} {\ partial \ boldsymbol {\ omega_j}} $$ display $$
para cualquier i y j. Esta derivada parcial muestra la dirección en la que cambiar
$ en línea $ \ boldsymbol {\ omega_j} $ en línea $ para ampliar
$ en línea $ L $ en línea $ . Para reducir necesitas dar un paso al costado
$ en línea $ - \ frac {\ parcial L (F (\ boldsymbol {x} _i))} {\ partial \ boldsymbol {\ omega_j}} $ en línea $ nada complicado
Entonces, el proceso de capacitación de la red se construye de la siguiente manera: varias veces en un ciclo pasamos por todo el conjunto de datos (esto se llama era), para cada objeto del conjunto de datos que consideramos
$ en línea $ L (\ hat {y} _i, y_i) $ en línea $ (esto se llama avance) y considere la derivada parcial
$ en línea $ \ parcial L $ en línea $ para todos los pesos
$ en línea $ \ boldsymbol {\ omega_j} $ en línea $ , luego actualice los pesos (esto se denomina paso hacia atrás).
Observo que aún no he introducido ninguna función y capa específica. Si en esta etapa no está claro qué hacer con todo esto, propongo continuar leyendo: habrá más matemáticas, pero ahora irá con ejemplos.
Matemáticas Parte 2 (difícil)
Función de error
Comenzaré desde el final y derivaré la función de error para el problema de clasificación. Para el problema de regresión, la derivación de la función de error se describe bien en el libro "Aprendizaje profundo". Inmersión en el mundo de las redes neuronales ".
Para simplificar, hay una red neuronal (NN) que separa las fotos de gatos de las fotos de perros, y hay un conjunto de fotos de gatos y perros para las cuales hay una respuesta correcta
$ inline $ y_ {true} $ inline $ .
$$ display $$ NN (imagen | \ Omega) = y_ {pred} $$ display $$
Todo lo que haré a continuación es muy similar al método de máxima verosimilitud. Por lo tanto, la tarea principal es encontrar la función de probabilidad. Si omitimos los detalles, entonces dicha función que compara la predicción de la red neuronal y la respuesta correcta, y si coinciden, da un gran valor, si no, viceversa. La probabilidad de una respuesta correcta viene a la mente con los parámetros dados:
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) $$ display $$
Y ahora haremos una finta que, al parecer, no se sigue de ninguna parte. Deje que la red neuronal dé una respuesta en forma de un vector bidimensional, cuya suma de los valores es 1. El primer elemento de este vector puede llamarse una medida de confianza de que el gato está en la foto, y el segundo elemento la medida de confianza de que el perro está en la foto. ¡Sí, es casi una probabilidad!
$$ display $$ NN (imagen | \ Omega) = \ left [\ begin {matrix} p_0 \\ p_1 \\\ end {matrix} \ right] $$ display $$
Ahora la función de probabilidad se puede reescribir como:
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) = p_ \ Omega (y_ {pred}) ^ t_ {0} * (1 - p_ \ Omega (y_ {pred})) ^ t_ {1} = \\ p_0 ^ {t_0} * p_1 ^ {t_1} $$ display $$
Donde
$ en línea $ t_0, t_1 $ en línea $ etiquetas de la clase correcta, por ejemplo, si
$ inline $ y_ {true} = cat $ inline $ entonces
$ en línea $ t_0 == 1, t_1 == 0 $ en línea $ si
$ en línea $ y_ {verdadero} = perro $ en línea $ entonces
$ en línea $ t_0 == 0, t_1 == 1 $ en línea $ . Por lo tanto, siempre se considera la probabilidad de una clase que debería haber sido predicha por una red neuronal (pero no necesariamente predicha por ella). Ahora esto se puede generalizar a cualquier número de clases (por ejemplo, m clases):
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) = \ prod_0 ^ m p_i ^ {t_i} $$ display $$
Sin embargo, en cualquier conjunto de datos hay muchos objetos (por ejemplo, N objetos). Quiero que la red neuronal dé la respuesta correcta en cada uno o la mayoría de los objetos. Y para esto, debe multiplicar los resultados de la fórmula anterior para cada objeto del conjunto de datos.
$$ display $$ MaximumLikelyhood = \ prod_ {j = 0} ^ N \ prod_ {i = 0} ^ m p_ {i, j} ^ {t_ {i, j}} $$ display $$
Para obtener buenos resultados, esta función necesita ser maximizada. Pero, en primer lugar, es más difícil de minimizar, porque tenemos un descenso de gradiente estocástico y todos los bollos para ello, solo asigna un signo menos, y en segundo lugar, es difícil trabajar con un trabajo enorme: es el logaritmo.
$$ display $$ CrossEntropyLoss = - \ sum \ limits_ {j = 0} ^ {N} \ sum \ limits_ {i = 0} ^ {m} t_ {i, j} \ cdot \ log (p_ {i, j }) $$ display $$
Genial El resultado fue entropía cruzada o, en el caso binario, logloss. Esta función es fácil de contar e incluso más fácil de diferenciar:
$$ display $$ \ frac {\ partial CrossEntropyLoss} {\ partial p_j} = - \ frac {\ boldsymbol {t_j}} {\ boldsymbol {p_ {j}}} $$ display $$
Necesita diferenciar para el algoritmo de retropropagación. Observo que la función de error no cambia la dimensión del vector. Si, como en el caso de MNIST, la salida es un vector de respuestas de 10 dimensiones, entonces al calcular la derivada, obtenemos un vector de derivadas de 10 dimensiones. Otra cosa interesante es que solo un elemento de la derivada no será cero, en el cual
$ en línea $ t_ {i, j} \ neq 0 $ en línea $ , es decir, con la respuesta correcta. Y cuanto menor sea la probabilidad de una respuesta correcta predicha por una red neuronal en un objeto dado, mayor será la función de error.
Características de activación
En la salida de cada capa completamente conectada de una red neuronal, debe estar presente una función de activación no lineal. Sin ella, es imposible entrenar una red neuronal significativa. Mirando hacia el futuro, una capa completamente conectada de una red neuronal es simplemente una multiplicación de los datos de entrada por una matriz de peso. En álgebra lineal, esto se llama un mapa lineal, una función lineal. La combinación de funciones lineales es también una función lineal. Pero esto significa que dicha función solo puede aproximar funciones lineales. Por desgracia, no es por eso que se necesitan redes neuronales.
Softmax
Por lo general, esta función se usa en la última capa de la red, ya que convierte el vector de la última capa en un vector de "probabilidades": cada elemento del vector se encuentra entre 0 y 1 y su suma es 1. No cambia la dimensión del vector.
$$ display $$ Softmax_i = \ frac {e ^ {x_i}} {\ sum \ limits_ {j} e ^ {x_j}} $$ display $$
Ahora pasemos a la búsqueda derivada. Desde
$ en línea $ \ boldsymbol {x} $ en línea $ Es un vector, y todos sus elementos siempre están presentes en el denominador, luego, al tomar la derivada, obtenemos el jacobiano:
$$ display $$ J_ {Softmax} = \ begin {cases} x_i - x_i \ cdot x_j, i = j \\ - x_i \ cdot x_j, i \ neq j \ end {cases} $$ display $$
Ahora sobre la propagación hacia atrás. El vector de derivados proviene de la capa anterior (por lo general, esta es una función de error)
$ en línea $ \ boldsymbol {dz} $ en línea $ . En caso
$ en línea $ \ boldsymbol {dz} $ en línea $ vino de una función de error en mnist,
$ en línea $ \ boldsymbol {dz} $ en línea $ - Vector de 10 dimensiones. Entonces el jacobiano tiene una dimensión de 10x10. Para obtener
$ en línea $ \ boldsymbol {dz_ {new}} $ en línea $ , que va más allá de la capa anterior (no olvide que vamos desde el final hasta el comienzo de la red cuando el error se propaga), necesitamos multiplicar
$ en línea $ \ boldsymbol {dz} $ en línea $ en
$ en línea $ J_ {Softmax} $ en línea $ (fila por columna):
$$ display $$ dz_ {new} = \ boldsymbol {dz} \ times J_ {Softmax} $$ display $$
En la salida, obtenemos un vector de derivadas de 10 dimensiones.
$ en línea $ \ boldsymbol {dz_ {new}} $ en línea $ .
Relu
$$ display $$ ReLU (x) = \ begin {cases} x, x> 0 \\ 0, x <0 \ end {cases} $$ display $$
ReLU comenzó a usarse de forma masiva después de 2011, cuando se publicó el artículo "Redes neuronales de rectificador profundo disperso". Sin embargo, dicha función se conocía anteriormente. El concepto de "poder de activación" es aplicable a ReLU (para más detalles, vea el libro "Aprendizaje profundo. Inmersión en el mundo de las redes neuronales"). Pero la característica principal que hace que ReLU sea más atractivo que otras funciones de activación es su cálculo derivado simple:
$$ display $$ d (ReLU (x)) = \ begin {cases} 1, x> 0 \\ 0, x <0 \ end {cases} $$ display $$
Por lo tanto, ReLU es computacionalmente más eficiente que otras funciones de activación (sigmoide, tangente hiperbólica, etc.).
Capa completamente conectada
Ahora es el momento de discutir una capa totalmente conectada. El más importante de todos los demás, porque es en esta capa donde se ubican todos los pesos, que deben ajustarse para que la red neuronal funcione bien. Una capa completamente conectada es simplemente una matriz de peso:
$$ display $$ W = | w_ {i, j} | $$ display $$
Se obtiene una nueva representación interna cuando la matriz de peso se multiplica por la columna de entrada:
$$ display $$ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $$ display $$
Donde
$ en línea $ \ boldsymbol {x} $ en línea $ tiene tamaño
$ inline $ input \ _shape $ inline $ y
$ en línea $ x_ {nuevo} $ en línea $ -
$ inline $ output \ _shape $ inline $ . Por ejemplo
$ en línea $ \ boldsymbol {x} $ en línea $ - vector de 784 dimensiones, y
$ en línea $ \ boldsymbol {x} _ {nuevo} $ en línea $ Es un vector de 100 dimensiones, entonces la matriz W tiene un tamaño de 100x784. Resulta que en esta capa es 100x784 = 78,400 pesos.
Con la propagación hacia atrás del error, uno necesita tomar la derivada con respecto a cada peso de esta matriz. Simplifique el problema y tome solo la derivada con respecto a
$ en línea $ w_ {1,1} $ en línea $ . Al multiplicar la matriz y el vector, el primer elemento del nuevo vector
$ en línea $ \ boldsymbol {x} _ {nuevo} $ en línea $ es igual a
$ en línea $ x_ {nuevo ~ 1} = w_ {1,1} \ cdot x_1 + ... + w_ {1.784} \ cdot x_ {784} $ en línea $ y la derivada
$ en línea $ x_ {nuevo ~ 1} $ en línea $ por
$ en línea $ w_ {1,1} $ en línea $ será simple
$ en línea $ x_1 $ en línea $ , solo necesita tomar la derivada de la cantidad anterior. Del mismo modo sucede para todos los demás pesos. Pero este no es un algoritmo de propagación de error, siempre y cuando sea solo una matriz de derivados. Debe recordar que de la siguiente capa a esta (el error va de principio a fin) viene un vector de gradiente de 100 dimensiones
$ en línea $ d \ boldsymbol {z} $ en línea $ . Primer elemento de este vector
$ en línea $ dz_1 $ en línea $ se multiplicará por todos los elementos de la matriz de derivados que "participaron" en la creación
$ en línea $ x_ {nuevo ~ 1} $ en línea $ , es decir, en
$ en línea $ x_1, x_2, ..., x_ {784} $ en línea $ . Del mismo modo, el resto de los elementos. Si traduces esto al lenguaje de álgebra lineal, entonces está escrito así:
$$ display $$ \ frac {\ partial L} {\ partial W} = (d \ boldsymbol {z}, ~ dW) = \ left (\ begin {matrix} dz_ {1} \ cdot \ boldsymbol {x} \ \ ... \\ dz_ {100} \ cdot \ boldsymbol {x} \ end {matrix} \ right) _ {100} $$ display $$
La salida es una matriz de 100x784.
Ahora necesita comprender qué transferir a la capa anterior. Para esto y para una mejor comprensión de lo que sucedió ahora, quiero escribir lo que sucedió al tomar derivados en esta capa en un lenguaje ligeramente diferente, para alejarme de los detalles de "lo que se multiplica por" a las funciones (nuevamente).
Cuando quería ajustar los pesos, quería tomar la derivada de la función de error para estos pesos:
$ en línea $ \ frac {\ partial L} {\ partial W} $ en línea $ . Se mostró arriba cómo tomar derivados de funciones de error y funciones de activación. Por lo tanto, podemos considerar tal caso (en
$ en línea $ d \ boldsymbol {z} $ en línea $ todas las derivadas de la función de error y las funciones de activación ya están sentadas):
$$ display $$ \ frac {\ partial L} {\ partial W} = d \ boldsymbol {z} \ cdot \ frac {\ partial \ boldsymbol {x} _ {new} (W)} {\ partial W} $ $ display $$
Esto se puede hacer, porque puedes considerar
$ en línea $ \ boldsymbol {x} _ {nuevo} $ en línea $ en función de W:
$ en línea $ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $ en línea $ .
Puede sustituir esto en la fórmula anterior:
$$ display $$ \ frac {\ partial L} {\ partial W} = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot \ boldsymbol {x}} {\ partial W} = d \ boldsymbol { z} \ cdot E \ cdot \ boldsymbol {x} $$ display $$
Donde E es una matriz que consta de unidades (NO una matriz de unidades).
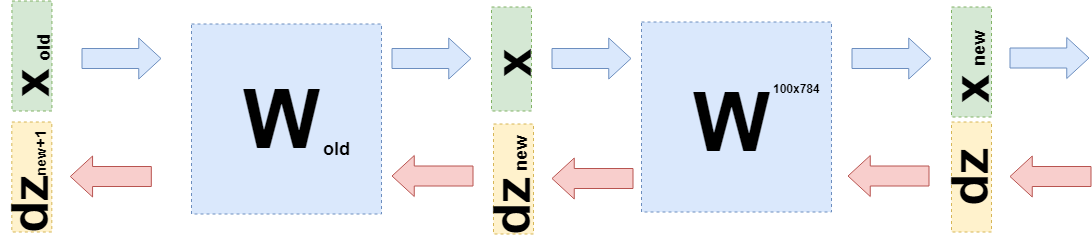
Ahora, cuando necesite tomar la derivada de la capa anterior (incluso para simplificar los cálculos, también será una capa completamente conectada, pero en el caso general no cambia nada), entonces debe considerar
$ en línea $ \ boldsymbol {x} $ en línea $ en función de la capa anterior
$ en línea $ \ boldsymbol {x} (W_ {old}) $ en línea $ :
$$ display $$ \ begin {reunido} \ frac {\ partial L} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot \ frac {\ partial \ boldsymbol {x} _ {new} (W )} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot \ boldsymbol {x} (W_ {old})} {\ partial W_ {old}} = \\ = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot W_ {old} \ cdot \ boldsymbol {x} _ {old}} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot W \ cdot E \ cdot \ boldsymbol {x} _ {old} = \\ = d \ boldsymbol {z} _ {new} \ cdot E \ cdot \ boldsymbol {x} _ {old} \ end {reunido} $$ mostrar $$
Exactamente
$ en línea $ d \ boldsymbol {z} _ {new} = d \ boldsymbol {z} \ cdot W $ en línea $ y necesitas enviar a la capa anterior.
Código
Este artículo está dirigido principalmente a explicar las matemáticas de las redes neuronales. Dedicaré muy poco tiempo al código.
Este es un ejemplo de implementación de la función de error:
class CrossEntropy: def forward(self, y_true, y_hat): self.y_hat = y_hat self.y_true = y_true self.loss = -np.sum(self.y_true * np.log(y_hat)) return self.loss def backward(self): dz = -self.y_true / self.y_hat return dz
La clase tiene métodos para el pase directo e inverso. En el momento del pase directo, la instancia de clase almacena los datos dentro de la capa y, en el momento del pase de retorno, los usa para calcular el gradiente. Las capas restantes se construyen de la misma manera. Gracias a esto, es posible escribir un neural completamente conectado en este estilo:
class MnistNet: def __init__(self): self.d1_layer = Dense(784, 100) self.a1_layer = ReLu() self.drop1_layer = Dropout(0.5) self.d2_layer = Dense(100, 50) self.a2_layer = ReLu() self.drop2_layer = Dropout(0.25) self.d3_layer = Dense(50, 10) self.a3_layer = Softmax() def forward(self, x, train=True): ... def backward(self, dz, learning_rate=0.01, mini_batch=True, update=False, len_mini_batch=None): ...
El código completo se puede encontrar
aquí .
También aconsejo estudiar este
artículo sobre Habré .
Conclusión
Espero haber podido explicar y demostrar que las redes neuronales están detrás de una matemática bastante simple y que esto no da miedo en absoluto. Sin embargo, para una comprensión más profunda, vale la pena intentar escribir su propia "bicicleta". Correcciones y sugerencias están felices de leer en los comentarios.