Cada desarrollador de Android utilizó RecyclerView para mostrar las listas, y cada uno enfrentó el problema de actualizar los datos en la lista hasta que apareció la clase mágica DiffUtil en 2016. Explicaré con los dedos cómo funciona realmente e intentaré disipar su magia.
Un poco de historia
Uno de los elementos más comunes en las aplicaciones móviles es la lista, en nuestro caso RecyclerView . Estas pueden ser listas de cualquier cosa: direcciones de oficina, listas de amigos en las redes sociales. redes, historial de pedidos en aplicaciones de taxi, etc. Todos estos casos están unidos por la necesidad de cambiar constantemente los datos de la lista a otros nuevos, cuando, por ejemplo, el usuario hizo un deslizamiento para actualizar, filtró la lista o de cualquier otra manera recibió un paquete de datos nuevos de la parte posterior.
Para implementar este comportamiento, el antepasado del desarrollador moderno de Android seleccionó manualmente qué datos y cómo cambiaron, y llamó a los métodos apropiados de RecyclerView . Sin embargo, todo cambió cuando Google lanzó la versión 25.1.0 de la Biblioteca de soporte, agregando DiffUtil allí, lo que le permitió transformar mágicamente la lista anterior en una nueva sin reconstruir completamente RecyclerView . En este artículo, DiffUtil la magia de DiffUtil y explicaré cómo funciona.
¿Cómo trabajar con DiffUtil?
Para trabajar con DiffUtil debe implementar DiffUtil.Callback , llame al método calculateDiff(@NonNull Callback cb) y aplique el DiffResult recibido al RecyclerView utilizando el método dispatchUpdatesTo() . ¿Qué sucede cuando se llama al método calucalteDiff(@NonNull Callback cd) ? Este método devuelve un DiffResult , que contiene un conjunto de operaciones para convertir la lista original en una nueva. Las actualizaciones se aplican mediante llamadas a los notifyItemRangeInserted , notifyItemRangeRemoved , notifyItemMoved y notifyItemRangeChanged . Los primeros tres métodos cambian la estructura de la lista, es decir, las posiciones de los elementos, sin cambiar los elementos en sí mismos y sin invocar onBindViewHolder() en ellos (con la excepción del elemento que se agrega). Este último cambia el elemento en sí y llama a onBindViewHolder() para cambiar la vista del elemento.
DiffUtil busca DiffUtil las dos listas utilizando el algoritmo Myers, que determina solo la presencia / ausencia de cambios, pero no sabe cómo encontrar el movimiento de los elementos. Para hacer esto, DiffUtil recorre las DiffUtil creadas por el algoritmo de Myers (más sobre esto más adelante), y luego busca movimientos. DiffResult está formado para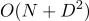 
si el algoritmo no verifica el movimiento de elementos y 
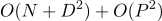, donde P es el número de elementos agregados y eliminados.
Algoritmo de Myers
A continuación, se considerará una explicación del algoritmo Myers en los dedos, al final del artículo se encontrarán enlaces a explicaciones matemáticas del algoritmo (así como otros artículos interesantes sobre el tema). Considere dos secuencias: BACAAC y CBCBAB. Es necesario escribir una secuencia de transformaciones sobre la primera secuencia, después de lo cual obtenemos la segunda. Escribimos las secuencias en la tabla de la siguiente manera: la lista anterior denotará los primeros elementos de las columnas, y la nueva lista será los primeros elementos de las filas.
Tache las celdas en las que se cruzan elementos idénticos de ambas secuencias:
Otra tarea es llegar desde la esquina superior izquierda de la matriz a la esquina inferior derecha en el menor número de pasos. Puede moverse a lo largo de caras horizontales y verticales. Si golpea el punto donde comienza la línea diagonal, debe moverse a lo largo de ella, pero el costo de dicho paso es 0. En consecuencia, el costo de un paso a lo largo de los bordes es 1.
Desde el punto (0; 0) podemos movernos hacia la derecha y hacia abajo. Al moverse hacia abajo, también debe ir en diagonal. El movimiento realizado en un paso se llama serpiente, en este caso se reciben 2 serpientes: (0; 0) -> (0; 1) y (0; 0) -> (1; 2). La flecha indica el final de la serpiente, es decir. si después del paso vertical / horizontal hay un paso obligatorio a lo largo de la diagonal, entonces la flecha estará en el paso a lo largo de la diagonal. La construcción completa de las serpientes desde el punto de partida hasta la final se muestra a continuación. Se omitieron algunas rutas en el video porque obviamente no fueron los más cortos.
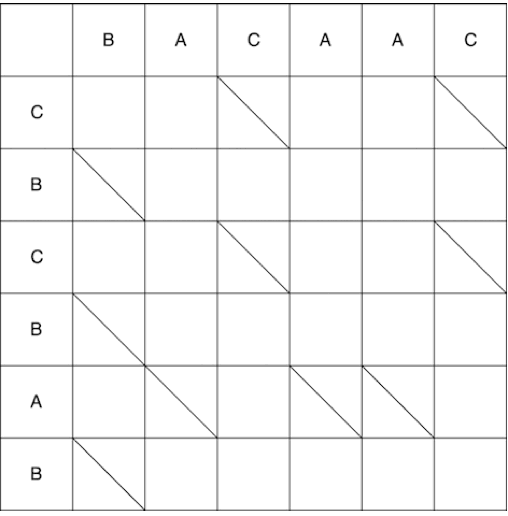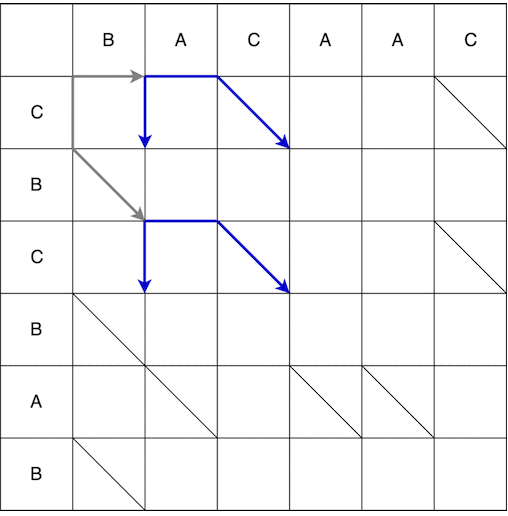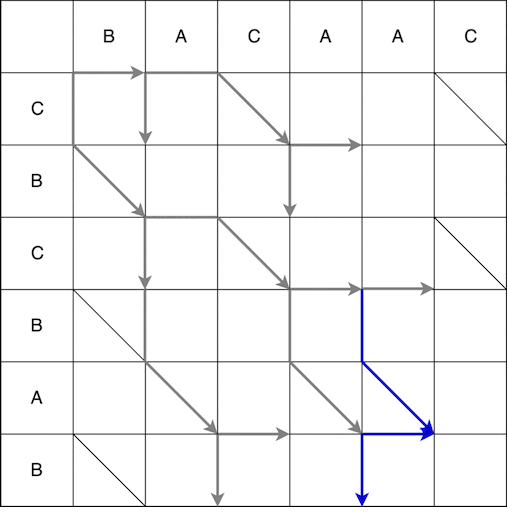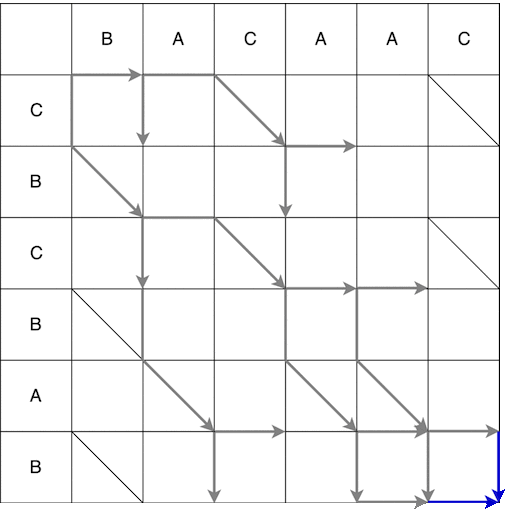
Como resultado, obtenemos varias rutas más cortas posibles, algunas de ellas se muestran a continuación.
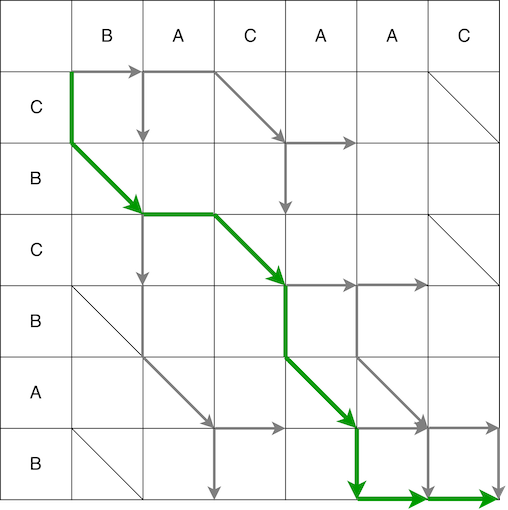
¿Cómo puede pasar una matriz desde el extremo izquierdo al extremo derecho ayudar a determinar la secuencia de acciones (script) para convertir una secuencia en otra? ¿Qué significan los pasos horizontales, verticales y diagonales? Un paso a lo largo de la matriz en una de las direcciones posibles son las acciones en la línea anterior:
- Paso horizontal: eliminar de la línea anterior
- Paso vertical - Agregar a línea antigua
- Paso diagonal: sin cambios
Usando la segunda ruta como ejemplo, comparamos la ruta y el script resultante. El primer paso es vertical, lo que significa que agregamos el carácter "C" a la posición 0 en la línea anterior.
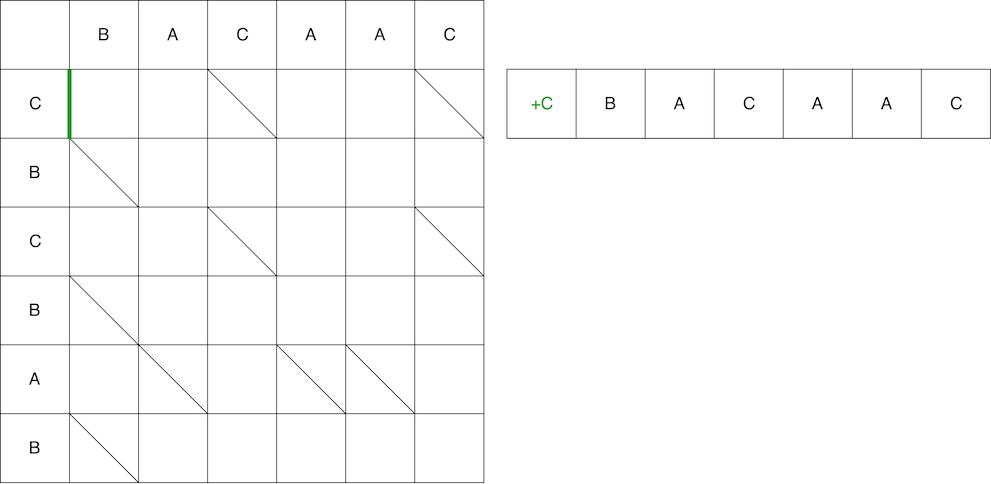
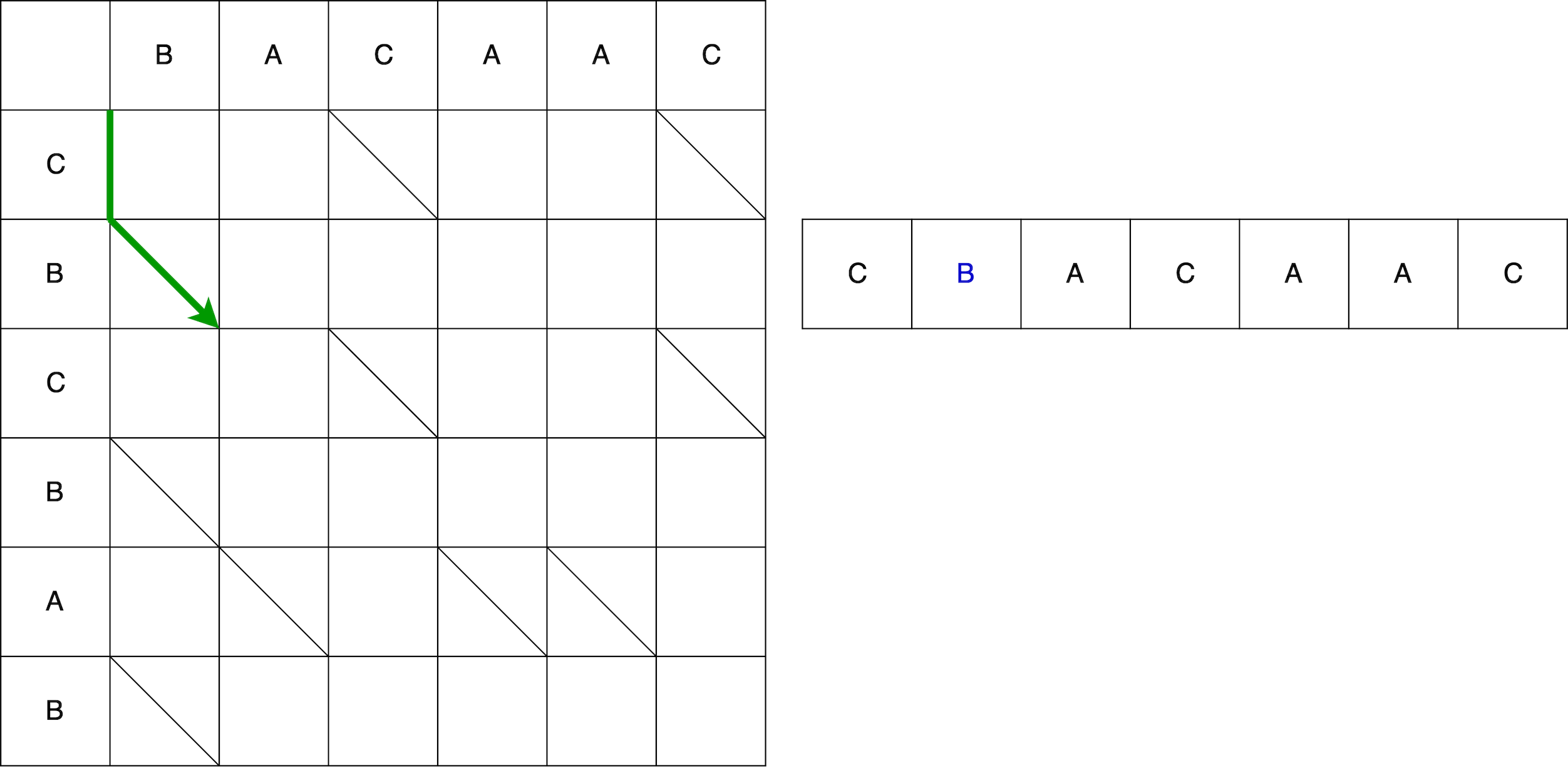
Sin embargo, esta no es toda la serpiente. A continuación, debemos movernos en diagonal. Al moverse en diagonal, el elemento B permanece sin cambios. Como resultado, la serpiente consiste en movimiento vertical + movimiento diagonal.
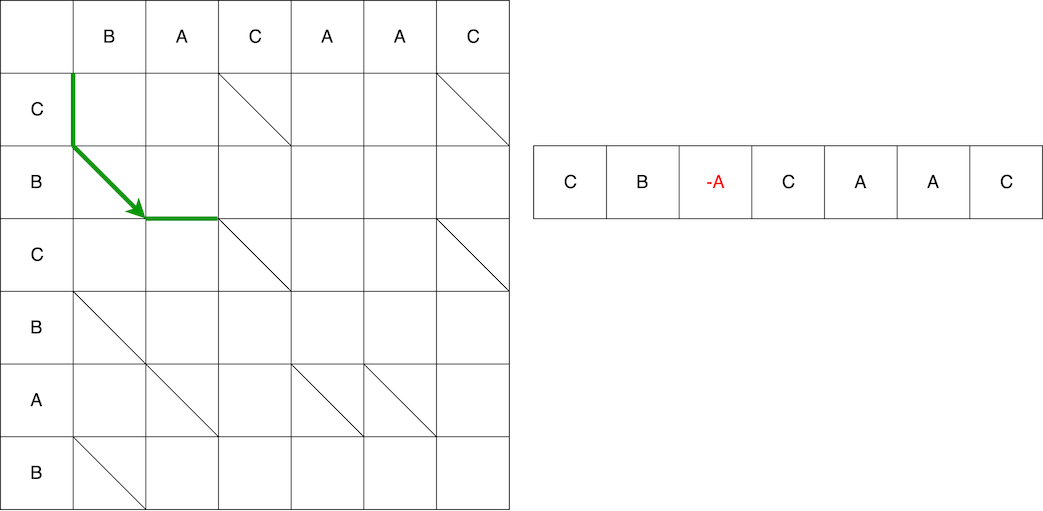
A continuación, la serpiente horizontalmente: elimine el elemento A. de la línea anterior
El video muestra la ruta completa de principio a fin con un cambio en la cadena de origen hasta que se convierte en la última.
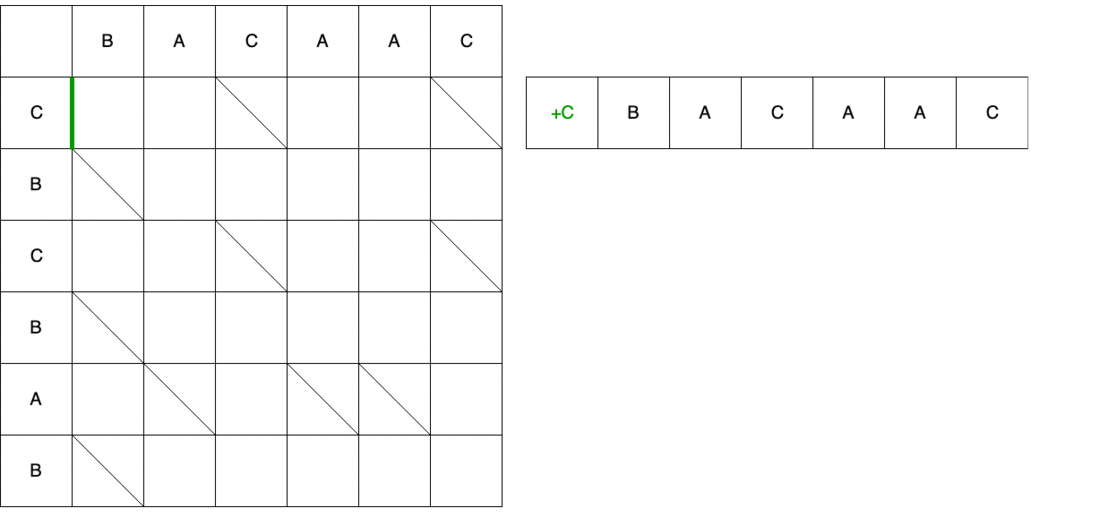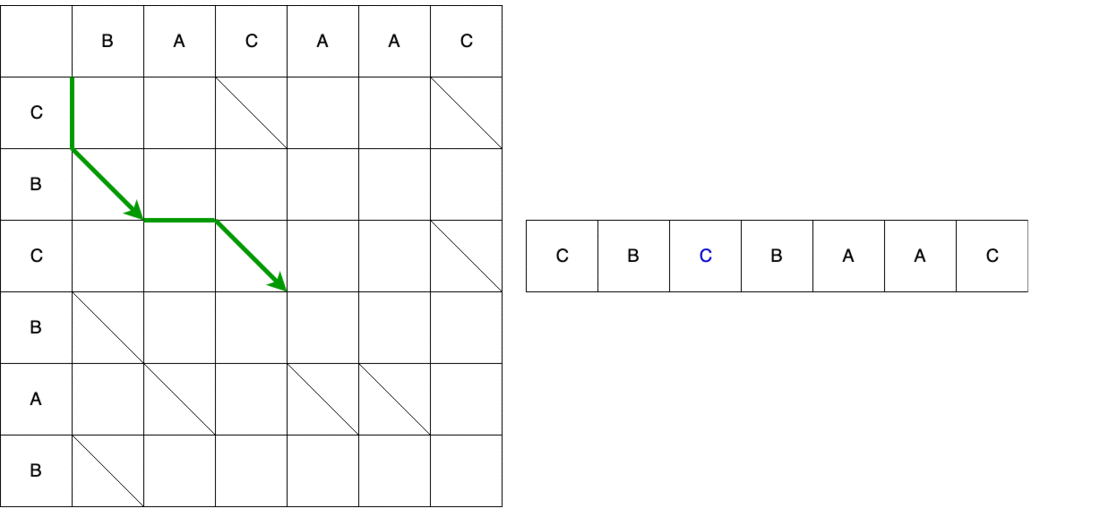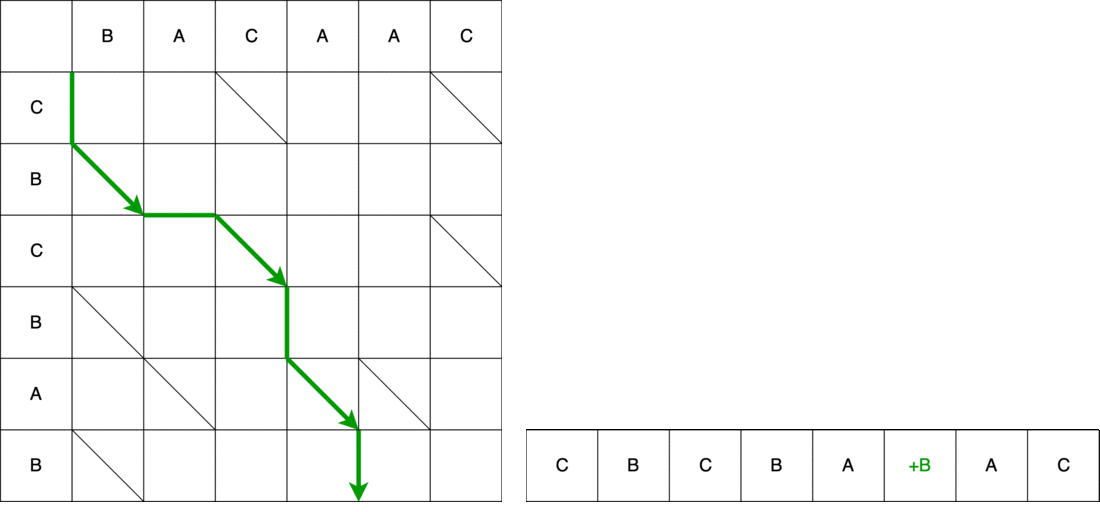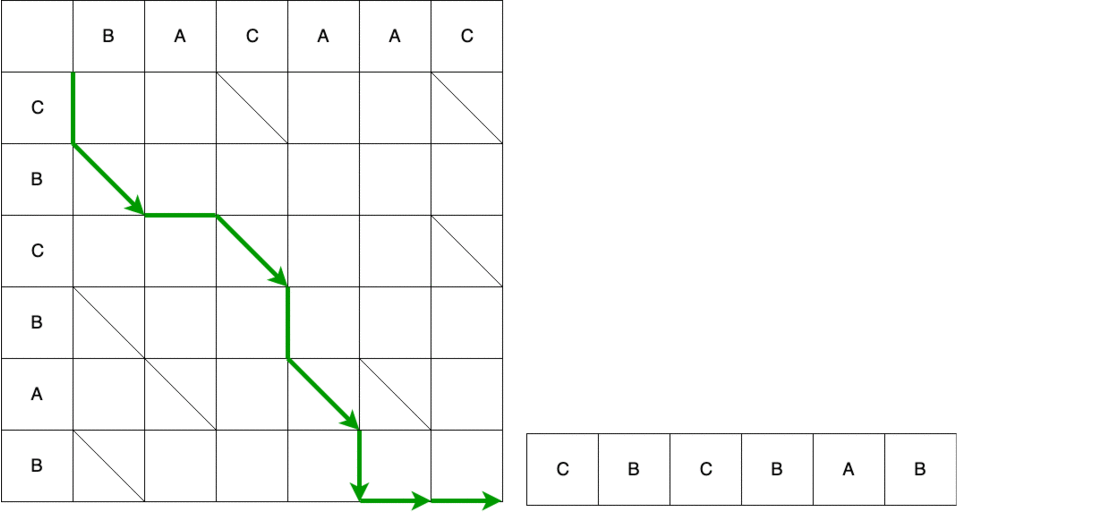
El resultado del algoritmo Myers es un script con un conjunto del número mínimo de acciones que se deben realizar para convertir una secuencia en otra. En DiffUtil el algoritmo Myers se usa para buscar diferentes elementos que están determinados por el método areItemsTheSame() . Además de formar una lista de serpientes, al pasar por las listas, el algoritmo Myers crea listas de estados de elementos de las listas antiguas y nuevas. Todos estos datos, así como el indicador detectMoves y la devolución de llamada implementada por el usuario, se pasan al constructor DiffResult(Callback callback, List<Snake> snakes, int[] oldItemStatuses, int[] newItemStatuses, boolean detectMoves) .
Mientras escribía este artículo, pude descubrir qué está sucediendo exactamente en DiffResult : el algoritmo pasa por las serpientes y establece banderas en los elementos (en las listas de estado), que determinan qué sucedió exactamente con el elemento. Al usar estos indicadores, al aplicar cambios a RecyclerView determina a qué método aplicar actualizaciones: notifyItemRangeInserted, notifyItemRangeRemoved, notifyItemMoved notifyItemRangeChanged . Con más detalle hablaré de esto la próxima vez.
Referencias