Redes neuronales y aprendizaje profundo, capítulo 3, parte 3: ¿cómo elegir hiperparámetros de redes neuronales?

Hasta ahora, no he explicado cómo elijo los valores de los hiperparámetros: la tasa de aprendizaje η, el parámetro de regularización λ, etc. Acabo de dar buenos valores de trabajo. En la práctica, cuando usa una red neuronal para atacar un problema, puede ser difícil encontrar buenos hiperparámetros. Imagine, por ejemplo, que nos acaban de informar sobre el problema MNIST y comenzamos a trabajar en él, sin saber nada sobre los valores de los hiperparámetros adecuados. Supongamos que tuvimos suerte por casualidad, y en los primeros experimentos elegimos muchos hiperparámetros como ya hicimos en este capítulo: 30 neuronas ocultas, un tamaño de mini paquete de 10, entrenamiento para 30 eras y el uso de entropía cruzada. Sin embargo, elegimos la tasa de aprendizaje η = 10.0 y el parámetro de regularización λ = 1000.0. Y esto es lo que vi con tal carrera:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 1030 / 10000 Epoch 1 training complete Accuracy on evaluation data: 990 / 10000 Epoch 2 training complete Accuracy on evaluation data: 1009 / 10000 ... Epoch 27 training complete Accuracy on evaluation data: 1009 / 10000 Epoch 28 training complete Accuracy on evaluation data: 983 / 10000 Epoch 29 training complete Accuracy on evaluation data: 967 / 10000 

¡Nuestra clasificación no funciona mejor que el muestreo aleatorio! ¡Nuestra red funciona como un generador de ruido aleatorio!

"Bueno, eso es fácil de arreglar", se podría decir, "simplemente reduzca los hiperparámetros como la velocidad de aprendizaje y la regularización". Desafortunadamente, a priori no tiene información sobre qué exactamente estos hiperparámetros necesita ajustar. Quizás el principal problema es que nuestras 30 neuronas ocultas nunca funcionarán, independientemente de cómo se seleccionen los otros hiperparámetros. ¿Quizás necesitamos al menos 100 neuronas ocultas? O 300? ¿O muchas capas ocultas? ¿O un enfoque diferente para la codificación de salida? ¿Quizás nuestra red está aprendiendo, pero necesitamos entrenarla más? ¿Quizás el tamaño de los mini paquetes es demasiado pequeño? ¿Tal vez nos hubiera ido mejor si volviéramos a la función cuadrática de valor? ¿Quizás debamos probar un enfoque diferente para inicializar los pesos? Y así sucesivamente. En el espacio de los hiperparámetros, es fácil perderse. Y esto realmente puede traer muchos inconvenientes si su red es muy grande o usa grandes cantidades de datos de entrenamiento, y puede entrenarla durante horas, días o semanas sin recibir resultados. En tal situación, su confianza comienza a pasar. ¿Quizás las redes neuronales fueron el enfoque equivocado para resolver su problema? ¿Quizás renunció y hizo apicultura?

En esta sección, explicaré algunos enfoques heurísticos que puede usar para configurar hiperparámetros en una red neuronal. El objetivo es ayudarlo a elaborar un flujo de trabajo que le permita configurar hiperparámetros bastante bien. Por supuesto, no puedo cubrir todo el tema de la optimización de hiperparámetros. Esta es un área enorme, y este no es un problema que pueda resolverse por completo, o de acuerdo con las estrategias correctas para resolver el acuerdo universal. Siempre existe la oportunidad de probar algún otro truco para extraer resultados adicionales de su red neuronal. Pero la heurística en esta sección debería darle un punto de partida.

Estrategia general

Cuando se usa una red neuronal para atacar un nuevo problema, la primera dificultad es obtener resultados no triviales de la red, es decir, exceder una probabilidad aleatoria. Esto puede ser sorprendentemente difícil, especialmente cuando se enfrenta a una nueva clase de tareas. Veamos algunas estrategias que se pueden usar para este tipo de dificultad.

Supongamos, por ejemplo, que usted es el primero en atacar la tarea MNIST. Empiezas con gran entusiasmo, pero el fracaso total de tu primera red es un poco desalentador, como se describe en el ejemplo anterior. Entonces necesita desmontar el problema en partes. Necesita deshacerse de todas las imágenes de entrenamiento y de apoyo, excepto las imágenes de ceros y unos. Luego, intente entrenar la red para distinguir 0 de 1. Esta tarea no solo es esencialmente más fácil que distinguir los diez dígitos, sino que también reduce la cantidad de datos de entrenamiento en un 80%, acelerando el aprendizaje en 5 veces. Esto le permite realizar experimentos mucho más rápido y le brinda la oportunidad de comprender rápidamente cómo crear una buena red.

Los experimentos pueden acelerarse aún más reduciendo la red a un tamaño mínimo que probablemente tenga una capacitación significativa. Si cree que es muy probable que la red [784, 10] pueda clasificar los dígitos MNIST mejor que una muestra aleatoria, entonces comience a experimentar con ella. Será mucho más rápido que el entrenamiento [784, 30, 10], y ya puedes hacerlo más tarde.

Se puede obtener otra aceleración de los experimentos aumentando la frecuencia de seguimiento. En el programa network2.py, monitoreamos la calidad del trabajo al final de cada era. Al procesar 50,000 imágenes por época, tenemos que esperar un tiempo bastante largo, aproximadamente 10 segundos por época en mi computadora portátil durante la capacitación en red [784, 30, 10], antes de recibir comentarios sobre la calidad de la capacitación en red. Por supuesto, diez segundos no son tan largos, pero si desea probar varias docenas de hiperparámetros diferentes, comienza a molestar, y si desea probar cientos o miles de opciones, simplemente devasta. La retroalimentación se puede recibir mucho más rápido al rastrear la precisión de la confirmación con mayor frecuencia, por ejemplo, cada 1000 imágenes de entrenamiento. Además, en lugar de utilizar el conjunto completo de 10.000 imágenes de confirmación, podemos obtener una estimación mucho más rápida utilizando solo 100 imágenes de confirmación. Lo principal es que la red ve suficientes imágenes para aprender realmente y para obtener una estimación de efectividad lo suficientemente buena. Por supuesto, nuestra network2.py aún no proporciona dicho seguimiento. Pero como muletas para lograr este efecto con fines ilustrativos, recortamos nuestros datos de entrenamiento a las primeras 1000 imágenes MNIST. Intentemos ver qué sucede (por la simplicidad del código, no utilicé la idea de dejar solo las imágenes 0 y 1; esto también se puede realizar con un poco más de esfuerzo).

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 ... 

Todavía obtenemos ruido puro, pero tenemos una gran ventaja: la retroalimentación se actualiza en fracciones de segundo, y no cada diez segundos. Esto significa que puede experimentar mucho más rápido con la selección de hiperparámetros, o incluso experimentar con muchos hiperparámetros diferentes casi simultáneamente.

En el ejemplo anterior, dejé el valor de λ igual a 1000.0, como antes. Pero dado que cambiamos el número de ejemplos de entrenamiento, necesitamos cambiar λ para que el debilitamiento de los pesos sea el mismo. Esto significa que cambiamos λ por 20.0. En este caso, resultará lo siguiente:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 12 / 100 Epoch 1 training complete Accuracy on evaluation data: 14 / 100 Epoch 2 training complete Accuracy on evaluation data: 25 / 100 Epoch 3 training complete Accuracy on evaluation data: 18 / 100 ... 

Si! Tenemos una señal No es particularmente bueno, pero lo hay. Esto ya se puede tomar como punto de partida y cambiar los hiperparámetros para intentar obtener mejoras adicionales. Supongamos que decidimos que necesitamos aumentar la velocidad de aprendizaje (como probablemente entendió, decidimos incorrectamente, por la razón que discutiremos más adelante, pero intentemos hacerlo por ahora). Para probar nuestra suposición, giramos η a 100.0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 Epoch 3 training complete Accuracy on evaluation data: 10 / 100 ... 

Todo esta mal! Aparentemente, nuestra suposición era incorrecta, y el problema no estaba en el valor muy bajo de la velocidad de aprendizaje. Intentamos ajustar η a un valor pequeño de 1.0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 62 / 100 Epoch 1 training complete Accuracy on evaluation data: 42 / 100 Epoch 2 training complete Accuracy on evaluation data: 43 / 100 Epoch 3 training complete Accuracy on evaluation data: 61 / 100 ... 

Eso esta mejor! Y así podemos continuar más allá, torciendo cada hiperparámetro y mejorando gradualmente la eficiencia. Después de estudiar la situación y encontrar un valor mejorado para η, procedemos a la búsqueda de un buen valor para λ. Luego realizaremos un experimento con una arquitectura más compleja, por ejemplo, con una red de 10 neuronas ocultas. Luego, nuevamente ajustamos los parámetros para η y λ. Luego aumentaremos la red a 20 neuronas ocultas. Un pequeño retoque de los hiperparámetros. Y así sucesivamente, evaluando la efectividad en cada paso utilizando parte de nuestros datos de respaldo y utilizando estas estimaciones para seleccionar los mejores hiperparámetros. En el proceso de mejoras, se necesita cada vez más tiempo para ver el efecto de los hiperparámetros de ajuste, por lo que podemos reducir gradualmente la frecuencia de seguimiento.

Como estrategia general, este enfoque parece prometedor. Sin embargo, quiero volver a ese primer paso en la búsqueda de hiperparámetros que permitan que la red aprenda al menos de alguna manera. De hecho, incluso en el ejemplo anterior, la situación era demasiado optimista. Trabajar con una red que no aprende nada puede ser extremadamente molesto. Puede ajustar los hiperparámetros durante varios días y no recibir respuestas significativas. Por lo tanto, me gustaría enfatizar una vez más que en las primeras etapas debe asegurarse de que pueda obtener comentarios rápidos de los experimentos. Intuitivamente, puede parecer que simplificar el problema y la arquitectura solo lo retrasará. De hecho, esto acelera el proceso, porque puede encontrar una red con una señal significativa mucho más rápido. Después de recibir dicha señal, a menudo podrá obtener mejoras rápidas al ajustar los hiperparámetros. Como en muchas situaciones de la vida, lo más difícil es comenzar el proceso.

De acuerdo, esta es una estrategia general. Ahora echemos un vistazo a las recomendaciones específicas para prescribir hiperparámetros. Me concentraré en la velocidad de aprendizaje η, el parámetro de regularización L2 λ y el tamaño del mini paquete. Sin embargo, muchos comentarios serán aplicables a otros hiperparámetros, incluidos los relacionados con la arquitectura de red, otras formas de regularización y algunos hiperparámetros, que aprenderemos en el libro más adelante, por ejemplo, el coeficiente de impulso.

Velocidad de aprendizaje

Supongamos que lanzamos tres redes MNIST con tres velocidades de aprendizaje diferentes, η = 0.025, η = 0.25 y η = 2.5, respectivamente. Dejaremos el resto de los hiperparámetros como estaban en las secciones anteriores: 30 eras, el tamaño del mini paquete es 10, λ = 5.0. También volveremos a usar las 50,000 imágenes de entrenamiento. Aquí hay un gráfico que muestra el comportamiento del costo de la capacitación (creado por el programa multiple_eta.py):



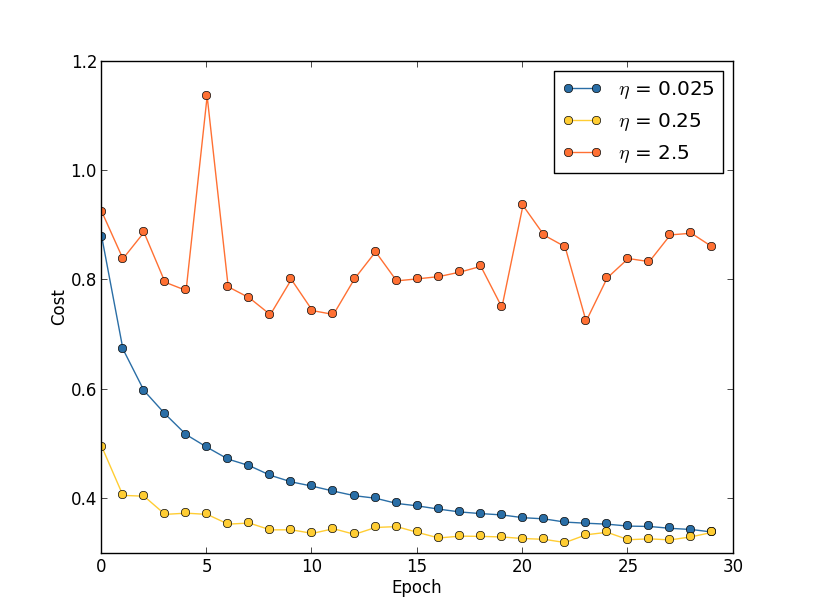
En η = 0.025, el costo disminuye suavemente hasta la última era. Con η = 0.25, el costo inicialmente disminuye, pero después de 20 épocas está saturado, por lo que la mayoría de los cambios resultan ser pequeñas y, obviamente, fluctuaciones aleatorias. Con η = 2.5, el costo varía mucho desde el principio. Para entender la razón de estas fluctuaciones, recordamos que el descenso de gradiente estocástico debería bajar gradualmente al valle de la función de costo:



Esta imagen ayuda a imaginar intuitivamente lo que está sucediendo, pero no es una explicación completa e integral. Más precisamente, pero brevemente, el descenso de gradiente utiliza una aproximación de primer orden para la función de costo para comprender cómo reducir el costo. Para η más grande, los miembros de una función de costo de orden más alto se vuelven más importantes y pueden dominar el comportamiento al romper el descenso del gradiente. Esto es especialmente probable al acercarse a los mínimos y mínimos locales de la función de costo, ya que al lado de tales puntos el gradiente se vuelve pequeño, lo que facilita el dominio de los miembros de un orden superior.

Sin embargo, si η es demasiado grande, entonces los pasos serán tan grandes que pueden saltar un mínimo, por lo que el algoritmo ascenderá desde el valle. Probablemente esto es lo que hace que el precio oscile en η = 2.5. La elección de η = 0.25 lleva al hecho de que los pasos iniciales realmente nos llevan a un mínimo de la función de costo, y solo cuando llegamos a ella, comenzamos a experimentar dificultades para saltar. Y cuando elegimos η = 0.025, no tenemos tales dificultades durante las primeras 30 épocas. Por supuesto, la elección de un valor tan pequeño de η crea otra dificultad, es decir, ralentiza el descenso de gradiente estocástico. El mejor enfoque sería comenzar con η = 0.25, aprender 20 eras y luego ir a η = 0.025. Más adelante discutiremos una tasa de aprendizaje tan variable. Mientras tanto, detengámonos en la cuestión de encontrar un valor adecuado para la velocidad de aprendizaje η.

Con esto en mente, podemos elegir η de la siguiente manera. Primero, evaluamos el valor umbral η al cual el costo de los datos de entrenamiento comienza a disminuir inmediatamente, pero no fluctúa y no aumenta. Esta estimación no tiene que ser precisa. El orden puede estimarse comenzando con η = 0.01. Si el costo disminuye en las primeras eras, entonces vale la pena intentar η = 0.1, luego 1.0, y así sucesivamente, hasta que encuentre un valor en el que el valor fluctúe o aumente en las primeras eras. Y viceversa, si el valor fluctúa o aumenta en las primeras épocas con η = 0.01, intente η = 0.001, η = 0.0001, hasta que encuentre el valor en el que el costo disminuye en las primeras eras. Este procedimiento le dará el orden del valor umbral η. Si lo desea, puede refinar su evaluación eligiendo el valor más alto para η, en el cual el costo disminuye en las primeras épocas, por ejemplo, η = 0.5 o η = 0.2 (no se necesita ultra precisión aquí). Esto nos da una estimación del valor umbral η.

El valor real de η, obviamente, no debe exceder el umbral seleccionado. De hecho, para que el valor η siga siendo útil durante muchas épocas, será mejor que use un valor dos veces menor que el umbral. Tal elección generalmente le permitirá aprender de muchas épocas sin ralentizar mucho su aprendizaje.

En el caso de los datos MNIST, seguir esta estrategia conducirá a una estimación del orden de umbral de η en 0.1. Después de un cierto refinamiento, obtenemos el valor η = 0.5. Siguiendo la receta anterior, debemos usar η = 0.25 para nuestra velocidad de aprendizaje. Pero, de hecho, descubrí que η = 0.5 funcionó bien durante 30 eras, por lo que no me preocupaba disminuirlo.

Todo esto parece bastante sencillo. Sin embargo, usar el costo de la capacitación para seleccionar η parece contradecir lo que dije antes: que elegimos hiperparámetros, evaluando la efectividad de la red utilizando datos confirmatorios seleccionados. De hecho, utilizaremos la precisión de la confirmación para seleccionar los hiperparámetros de regularización, el tamaño del mini paquete y parámetros de red como el número de capas y neuronas ocultas, etc. ¿Por qué hacemos las cosas de manera diferente con la velocidad de aprendizaje? Honestamente, esta elección se debe a mis preferencias estéticas personales y probablemente sea parcial. El argumento es que otros hiperparámetros deberían mejorar la precisión de la clasificación final en el conjunto de prueba, por lo que tiene sentido elegirlos en función de la precisión de la confirmación. Sin embargo, la tasa de aprendizaje solo afecta indirectamente la precisión de la clasificación final. Su objetivo principal es controlar el tamaño del paso del descenso del gradiente y hacer un seguimiento del costo del entrenamiento de la mejor manera para reconocer un tamaño de paso demasiado grande. Pero aún así esta es una preferencia estética personal. En las primeras etapas del entrenamiento, el costo del entrenamiento generalmente disminuye solo si aumenta la precisión de la confirmación, por lo que en la práctica no debería importar qué criterios usar.

Usar una parada temprana para determinar la cantidad de eras de entrenamiento

Como mencionamos en este capítulo, una parada temprana significa que al final de cada era, necesitamos calcular la precisión de la clasificación en los datos de soporte. Cuando deja de mejorar, dejamos de funcionar. Como resultado, establecer el número de eras se convierte en un asunto simple. En particular, esto significa que no necesitamos determinar específicamente cómo la cantidad de épocas depende de otros hiperparámetros. Esto sucede de forma automática. Además, una parada temprana también nos impide automáticamente volver a entrenar. Esto, por supuesto, es bueno, aunque podría ser útil desactivar la parada temprana en las primeras etapas de los experimentos para que pueda ver signos de reentrenamiento y usarlos para ajustar el enfoque de la regularización.

Para implementar el RO, necesitamos describir más específicamente lo que significa "detener la mejora de la precisión de la clasificación". Como hemos visto, la precisión puede ir muy lejos, incluso cuando la tendencia general está mejorando. Si nos detenemos por primera vez, cuando la precisión disminuye, es casi seguro que no alcanzaremos posibles mejoras adicionales. El mejor enfoque es dejar de aprender si la mejor precisión de clasificación no mejora durante mucho tiempo. Supongamos, por ejemplo, que estamos involucrados en MNIST. Entonces podemos decidir detener el proceso si la precisión de la clasificación no ha mejorado en las últimas diez eras. Esto garantiza que no nos detenemos demasiado pronto debido a fallas en el entrenamiento, pero no esperaremos para siempre por cualquier mejora que no suceda.

Esta regla de "no mejora en diez eras" es adecuada para el estudio inicial de MNIST. Sin embargo, las redes a veces pueden alcanzar una meseta cerca de cierta precisión de clasificación, permanecer allí durante bastante tiempo y luego comenzar a mejorar nuevamente. Si necesita lograr un rendimiento muy bueno, entonces la regla de "ninguna mejora en diez eras" podría ser demasiado agresiva para eso. Por lo tanto, recomiendo usar la regla "sin mejora en diez eras" para los experimentos primarios, y gradualmente adopte reglas más suaves cuando comience a comprender mejor el comportamiento de su red: "no hay mejora en más de veinte eras", "no hay mejora en más de cincuenta eras", etc. más lejos ¡Por supuesto, esto nos da otro hiperparámetro para la optimización! Pero en la práctica, este hiperparámetro suele ser fácil de ajustar para obtener buenos resultados. Y para tareas que no sean MNIST, la regla de "no mejora en diez eras" puede ser demasiado agresiva o no lo suficientemente agresiva, dependiendo de los detalles de una tarea en particular.Sin embargo, habiendo experimentado un poco, generalmente es bastante fácil encontrar una estrategia adecuada de parada temprana.

Todavía no hemos utilizado una parada temprana en nuestros experimentos con MNIST. Esto se debe al hecho de que hicimos muchas comparaciones de diferentes enfoques de aprendizaje. Para tales comparaciones, es útil usar el mismo número de eras en todos los casos. Sin embargo, vale la pena cambiar network2.py introduciendo el RO en el programa.

Las tareas

• Modifique network2.py para que el PO aparezca allí de acuerdo con la regla "sin cambios para n épocas", donde n es un parámetro configurable.
• Piense en una regla de detención temprana que no sea "sin cambios en las eras". Idealmente, la regla debería buscar un compromiso entre obtener precisión con una alta confirmación y un tiempo de entrenamiento bastante corto. Agregue una regla a network2.py y ejecute tres experimentos que comparen la precisión de la validación y el número de eras de entrenamiento con la regla "sin cambios en 10 eras".

Plan de cambio de velocidad de aprendizaje

Mientras mantuvimos la velocidad de aprendizaje η constante. Sin embargo, a menudo es útil modificarlo. En las primeras etapas del proceso de capacitación, es muy probable que se asignen pesos completamente incorrectos. Por lo tanto, será mejor usar una alta tasa de entrenamiento, lo que hará que los pesos cambien más rápido. Entonces puede reducir la velocidad del entrenamiento para hacer un ajuste más fino de las escalas.

¿Cómo delineamos un plan para cambiar la velocidad de aprendizaje? Aquí puede aplicar muchos enfoques. Una opción natural es usar la misma idea básica que en RO. Mantenemos constante la velocidad de aprendizaje hasta que la precisión de la confirmación comience a deteriorarse. Luego reducimos el CO en cierta cantidad, digamos, dos o diez veces. Repetimos esto muchas veces hasta que el CO sea 1024 (o 1000) veces menor que el inicial. Y termina el entrenamiento.

Un plan para cambiar la velocidad de aprendizaje puede mejorar la eficiencia y también abre enormes oportunidades para elegir un plan. Y esto puede ser un dolor de cabeza: puede pasar siempre optimizando el plan. Para los primeros experimentos, sugeriría usar un solo valor constante de CO. Esto le dará una buena primera aproximación. Más adelante, si desea obtener la mejor eficiencia de la red, vale la pena experimentar con el plan para cambiar la velocidad de aprendizaje como lo describí. Un trabajo científico bastante fácil de leer de 2010 demuestra las ventajas de las velocidades de aprendizaje variables al atacar MNIST.

Ejercicio

• Modifique network2.py para que implemente el siguiente plan para cambiar la velocidad de aprendizaje: reduzca a la mitad el CR cada vez que la precisión de la confirmación satisfaga la regla de "no cambiar en 10 épocas", y deje de aprender cuando la velocidad de aprendizaje descienda a 1/128 de la inicial.

El parámetro de regularización λ

Recomiendo comenzar sin regularización (λ = 0,0) y determinar el valor de η, como se indicó anteriormente. Usando el valor seleccionado de η, podemos usar los datos de soporte para seleccionar un buen valor de λ. Comience con λ = 1.0 (no tengo un buen argumento a favor de tal elección), y luego aumente o disminuya en 10 veces para aumentar la eficiencia al trabajar con datos de confirmación. Habiendo encontrado el orden correcto de magnitud, podemos ajustar el valor de λ con mayor precisión. Después de esto, es necesario volver a la optimización η nuevamente.

Ejercicio

• , , λ η. , λ? , η?

Si usa las recomendaciones de esta sección, verá que los valores seleccionados de η y λ no siempre se corresponden exactamente con los que usé anteriormente. Es solo que el libro tiene limitaciones de texto, lo que a veces hace que sea poco práctico optimizar los hiperparámetros. Piense en todas las comparaciones de los diferentes enfoques de entrenamiento en los que hemos estado trabajando: comparando la función de costo cuadrático y la entropía cruzada, los métodos antiguos y nuevos de inicializar pesos, correr con y sin regularización, etc. Para que estas comparaciones tengan sentido, traté de no cambiar los hiperparámetros entre los enfoques comparados (o escalarlos correctamente). Por supuesto, no hay ninguna razón para que los mismos hiperparámetros sean óptimos para todos los diferentes enfoques de aprendizaje, por lo que los hiperparámetros que uso fueron el resultado de un compromiso.

Como alternativa, podría intentar optimizar al máximo todos los hiperparámetros para cada enfoque de aprendizaje. Sería un enfoque mejor y más honesto, ya que tomaríamos lo mejor de cada enfoque de aprendizaje. Sin embargo, hicimos docenas de comparaciones, y en la práctica esto sería demasiado costoso computacionalmente. Por lo tanto, decidí comprometerme, usar opciones de hiperparámetros suficientemente buenas (pero no necesariamente óptimas).

Mini Pack Size

¿Cómo elegir el tamaño del mini-paquete? Para responder a esta pregunta, primero supongamos que participamos en capacitación en línea, es decir, usamos un mini paquete de tamaño 1.

El problema obvio con el aprendizaje en línea es que el uso de mini-paquetes que consisten en un solo ejemplo de capacitación conducirá a serios errores al estimar el gradiente. Pero, de hecho, estos errores no presentarán un problema tan grave. La razón es que las estimaciones de gradiente individuales no tienen que ser muy precisas. Solo necesitamos obtener una estimación suficientemente precisa para que nuestra función de costos disminuya. Es como si estuviera tratando de llegar al polo norte magnético, pero tendría una brújula poco confiable, con cada medición equivocada en 10-20 grados. Si revisas la brújula con bastante frecuencia y, en promedio, indicará la dirección correcta, eventualmente podrás llegar al polo norte magnético.

Dado este argumento, parece que deberíamos usar el aprendizaje en línea. Pero en realidad la situación es algo más complicada. En la tarea del último capítulo, señalé que para calcular la actualización de gradiente para todos los ejemplos en el mini paquete, puede usar técnicas matriciales al mismo tiempo, en lugar de un bucle. Dependiendo de los detalles de su hardware y la biblioteca de álgebra lineal, puede resultar mucho más rápido calcular la estimación para el mini-paquete de, digamos, 100 que calcular la estimación de gradiente para el mini-paquete en un ciclo para 100 ejemplos de entrenamiento. Esto puede resultar, por ejemplo, solo 50 veces más lento, y no 100.

Al principio parece que esto no nos ayuda mucho. Con un tamaño de mini paquete de 100, la regla de entrenamiento para pesas se ve así:

$$

$$w \rightarrow w' = w-\eta \frac{1}{100} \sum_x \nabla C_x \tag{100}$$

donde el resumen va sobre los ejemplos de entrenamiento en el mini paquete. Comparar con

$$

$$w \rightarrow w' = w-\eta \nabla C_x \tag{101}$$

para el aprendizaje en línea Incluso si tarda 50 veces más tiempo en actualizar el mini-paquete, la capacitación en línea parece ser la mejor opción, ya que nos actualizaremos más a menudo. Pero supongamos, sin embargo, que en el caso del mini-paquete, aumentamos la velocidad de aprendizaje en 100 veces, luego la regla de actualización se convierte en:

$$

$$w \rightarrow w' = w-\eta \sum_x \nabla C_x \tag{102}$$

Esto es similar a 100 etapas separadas de aprendizaje en línea con una velocidad de aprendizaje de η. Sin embargo, un paso en el aprendizaje en línea solo toma 50 veces más tiempo. Por supuesto, en realidad esto no es exactamente 100 niveles de aprendizaje en línea, ya que en el minipaquete todos los ∇C _x se evalúan para el mismo conjunto de pesos, en contraste con el aprendizaje acumulativo que ocurre en el caso en línea. Y, sin embargo, parece que el uso de mini paquetes más grandes acelerará el proceso.

Teniendo en cuenta todos estos factores, elegir el mejor tamaño de mini paquete es un compromiso. Elija demasiado pequeño y no obtenga el beneficio completo de buenas bibliotecas matriciales optimizadas para hardware rápido. Elija demasiado grande y no actualizará el peso con la frecuencia suficiente. Debe elegir un valor de compromiso que maximice la velocidad de aprendizaje. Afortunadamente, la elección del tamaño de mini paquete a la que se maximiza la velocidad es relativamente independiente de otros hiperparámetros (excepto la arquitectura general), por lo tanto, para encontrar un buen tamaño de mini paquete, no es necesario optimizarlos. Por lo tanto, será suficiente usar valores aceptables (no necesariamente óptimos) para otros hiperparámetros, y luego probar varios tamaños diferentes de mini-paquetes, escalando η, como se indicó anteriormente.Cree un gráfico de la precisión de la confirmación en función del tiempo (¡tiempo transcurrido real, no eras!), Y elija un tamaño de mini paquete que ofrezca la mejora de rendimiento más rápida. Con el tamaño de mini paquete seleccionado, puede proceder a optimizar otros hiperparámetros.

Por supuesto, como ya sin duda entendió, en nuestro trabajo no llevé a cabo tal optimización. En nuestra implementación de la Asamblea Nacional, no se utiliza en absoluto un enfoque rápido para actualizar los mini paquetes. Simplemente utilicé el mini-paquete tamaño 10 sin comentarlo ni explicarlo, en casi todos los ejemplos. En general, podríamos acelerar el aprendizaje al reducir el tamaño del mini-paquete. No hice esto, en particular, porque mis experimentos preliminares sugirieron que la aceleración sería bastante modesta. Pero en implementaciones prácticas, definitivamente nos gustaría implementar el enfoque más rápido para actualizar los mini paquetes, y tratar de optimizar su tamaño para maximizar la velocidad general.

Técnicas automatizadas

Describí estos enfoques heurísticos como algo que necesita ser ajustado a mano. La optimización manual es una buena manera de tener una idea de cómo funciona NS. Sin embargo, y, por cierto, no es sorprendente que ya se haya realizado una gran cantidad de trabajo en la automatización de este proyecto. Una técnica común es una búsqueda de cuadrícula que tamiza sistemáticamente una cuadrícula en el espacio de los hiperparámetros. En 2012 se puede encontrar una descripción general de los logros y limitaciones de esta técnica (así como recomendaciones sobre alternativas de fácil implementación) . Se han propuesto muchas técnicas sofisticadas. No los revisaré todos, pero quiero señalar el prometedor trabajo de 2012, utilizando la optimización bayesiana de hiperparámetros. El código del trabajo está abierto a todos. , y con cierto éxito fue utilizado por otros investigadores.

Resumir

Usando las reglas de práctica que he descrito, no obtendrá los mejores resultados de su PS de todos los posibles. Pero es probable que le brinden un buen punto de partida y una base para futuras mejoras. En particular, básicamente describí hiperparámetros de forma independiente. En la práctica, hay una conexión entre ellos. Puede experimentar con η, decidir que ha encontrado el valor correcto, luego comenzar a optimizar λ y descubrir que viola su optimización η. En la práctica, es útil moverse en diferentes direcciones, acercándose gradualmente a los buenos valores. Sobre todo, tenga en cuenta que los enfoques heurísticos que he descrito son simples reglas de práctica, pero no algo tallado en piedra. Debe buscar señales de que algo no funciona y tener ganas de experimentar. En particularControle cuidadosamente el comportamiento de su red neuronal, especialmente la precisión de la confirmación.

La complejidad de la elección de los hiperparámetros se ve agravada por el hecho de que el conocimiento práctico de su elección se extiende a muchos trabajos y programas de investigación, y a menudo solo está en la cabeza de los profesionales individuales. Hay una gran cantidad de trabajo con descripciones de qué hacer (a menudo en conflicto entre sí). Sin embargo, hay varios trabajos particularmente útiles que sintetizan y resaltan una gran parte de este conocimiento. En el Joshua Benji partir de 2012 da consejos prácticos sobre el uso de descenso de gradiente de propagación hacia atrás y la formación de la Asamblea Nacional, incluyendo la Asamblea Nacional y profundo. Benjio describe muchos de los detalles con mucho más detalle. Que yo, incluida una búsqueda sistemática de hiperparámetros. Otro buen trabajo es el trabajo.1998 Yanna Lekuna y otros. Ambas obras aparecen en el libro extremadamente útil de 2012, que contiene muchos trucos de uso frecuente en la Asamblea Nacional: " Redes neuronales: trucos artesanales ". El libro es costoso, pero muchos de sus artículos fueron publicados en Internet por sus autores, y se pueden encontrar en los motores de búsqueda.

De estos artículos, y especialmente de nuestros propios experimentos, una cosa queda clara: el problema de optimizar los hiperparámetros no se puede resolver por completo. Siempre hay otro truco que puedes intentar para mejorar la eficiencia. Los escritores dicen que un libro no puede terminarse, sino que solo puede descartarse. Lo mismo es cierto para la optimización NS: el espacio de los hiperparámetros es tan grande que la optimización no se puede completar, sino que solo se puede detener, dejando el NS a los descendientes. Por lo tanto, su objetivo será desarrollar un flujo de trabajo que le permita llevar a cabo rápidamente una buena optimización, mientras le da la oportunidad de probar opciones de optimización más detalladas si es necesario.

Las dificultades con la selección de hiperparámetros hacen que algunas personas se quejen de que los NS requieren demasiado esfuerzo en comparación con otras técnicas de MO. He escuchado muchas variantes de quejas como: “Sí, un NS bien ajustado puede brindar la mejor eficiencia al resolver un problema. Pero por otro lado, puedo probar un bosque aleatorio [o SVM, o cualquier otra tecnología favorita], y simplemente funciona. No tengo tiempo para averiguar qué NA es el adecuado para mí ". Por supuesto, desde un punto de vista práctico, es bueno tener técnicas fáciles de usar con un amigo. Esto es especialmente bueno cuando recién está comenzando a trabajar con una tarea, y todavía no está claro si el MO puede ayudarlo a resolverlo. Por otro lado, si es importante para usted lograr resultados óptimos, es posible que deba probar varios enfoques que requieren un conocimiento más especializado. Seria genialsi MO siempre fue fácil, pero no hay razones por las que debería ser a priori trivial.

Otras tecnicas

Cada una de las técnicas desarrolladas en este capítulo es valiosa en sí misma, pero esta no es la única razón por la que las describí. Es más importante familiarizarse con algunos de los problemas que pueden surgir en el campo de NA y con un estilo de análisis que pueda ayudar a superarlos. En cierto modo, estamos aprendiendo a pensar sobre el NS. En el resto de este capítulo, describiré brevemente un conjunto de otras técnicas. Sus descripciones no serán tan profundas como en las anteriores, pero deben transmitir algunas sensaciones con respecto a la variedad de técnicas encontradas en el campo de NA.

Variaciones del descenso de gradiente estocástico

El descenso de gradiente estocástico a través de la propagación hacia atrás nos sirvió durante el ataque al problema de clasificar números escritos a mano de MNIST. Sin embargo, existen muchos otros enfoques para optimizar la función de costos, y algunas veces muestran una eficiencia superior a la del descenso de gradiente estocástico con mini paquetes. En esta sección, describo brevemente dos de estos enfoques, el hessiano y el impulso.

Arpillera

Para comenzar, dejemos de lado a la Asamblea Nacional. En cambio, simplemente consideramos el problema abstracto de minimizar la función de costo C de muchas variables, w = w1, w2, ..., es decir, C = C (w). Según el teorema de Taylor, la función de costo en el punto w puede ser aproximada:

$$

$$C(w+\Delta w) = C(w) + \sum_j \frac{\partial C}{\partial w_j} \Delta w_j \nonumber \\ + \frac{1}{2} \sum_{jk} \Delta w_j \frac{\partial^2 C}{\partial w_j \partial w_k} \Delta w_k + \ldots \tag{103}$$

Podemos reescribirlo de manera más compacta como

$$

$$C(w+\Delta w) = C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w + \ldots \tag{104}$$

donde ∇C es el vector de gradiente ordinario, y H es la matriz, conocida como la matriz de Hesse , en lugar de jk en la que ∂ ² C / ∂w _j ∂w _k . Supongamos que aproximamos C al abandonar los términos de orden superior que se esconden detrás de los puntos suspensivos en la fórmula:

$$

$$C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w \tag{105}$$

Usando álgebra, se puede demostrar que la expresión en el lado derecho se puede minimizar seleccionando:

$$

$$\Delta w = -H^{-1} \nabla C \tag{106}$$

Hablando estrictamente, para que esto sea solo un mínimo, y no solo un extremo, debemos suponer que la matriz de Hesse es más positiva. Intuitivamente, esto significa que la función C es como un valle, no una montaña o una silla de montar.

Si (105) es una buena aproximación a la función de costo, se espera que la transición del punto w al punto w + Δw = w - H - 1 −C reduzca significativamente la función de costo. Esto ofrece un posible algoritmo de minimización de costos:

• Seleccione el punto de partida w.
• Actualice w a un nuevo punto, w ′ = w - H ⁻¹ ∇C, donde Hessian H y ∇C se calculan en w.
• w' , w′′=w′−H′ ⁻¹ ∇′C, H ∇C w'.
• ...

En la práctica, (105) es solo una aproximación, y es mejor dar pasos más pequeños. Haremos esto actualizando constantemente w por Δw = −ηH - 1∇C, donde η es la velocidad de aprendizaje.

Este enfoque para minimizar la función de costos se conoce como optimización de Hesse. Hay resultados teóricos y empíricos que muestran que los métodos de Hesse convergen al mínimo en menos pasos que un descenso de gradiente estándar. En particular, al incluir información sobre los cambios de segundo orden en la función de costos, es posible evitar muchas patologías encontradas en el descenso de gradiente en el enfoque de Hesse. Además, hay versiones del algoritmo de retropropagación que se pueden usar para calcular el Hessian.

Si la optimización de Hesse es tan genial, ¿por qué no la usamos en nuestro NS? Desafortunadamente, aunque tiene muchas propiedades deseables, hay una muy indeseable: es muy difícil de poner en práctica. Parte del problema es el gran tamaño de la matriz de Hesse. Supongamos que tenemos un NS con 10 ⁷ pesos y compensaciones. Luego, en la matriz de Hesse correspondiente habrá 10 ⁷ × 10 ⁷ = 10 ¹⁴ elementos. Demasiados! Como resultado , resulta muy difícil calcular H ⁻¹ ∇C en la práctica. Pero esto no significa que sea inútil saber de ella. Muchas opciones de descenso de gradiente están inspiradas en la optimización de Hesse, simplemente evitan el problema de matrices excesivamente grandes. Echemos un vistazo a una de esas técnicas, el descenso por gradiente de impulso.

Descenso de gradiente basado en impulsos

Intuitivamente, la ventaja de la optimización de Hesse es que incluye no solo información sobre el gradiente, sino también información sobre su cambio. El descenso de gradiente basado en impulsos se basa en una intuición similar, pero evita grandes matrices de segundas derivadas. Para comprender la técnica de impulso, recordemos nuestra primera imagen de descenso en gradiente, en la que examinamos una bola rodando por un valle. Luego vimos que el descenso en gradiente, contrario a su nombre, solo se asemeja ligeramente a una bola que cae al fondo. La técnica de pulso cambia el descenso del gradiente en dos lugares, lo que lo hace más parecido a una imagen física. Primero, introduce el concepto de "velocidad" para los parámetros que estamos tratando de optimizar. El gradiente está tratando de cambiar la velocidad, no la "ubicación" directamente, similar a cómo las fuerzas físicas cambian la velocidad,y solo afecta indirectamente la ubicación. En segundo lugar, el método de impulso es un tipo de término de fricción que reduce gradualmente la velocidad.

Demos una definición matemáticamente más precisa. Introducimos las variables de velocidad v = v1, v2, ..., una para cada variable correspondiente w _j (en la red neuronal, estas variables incluyen naturalmente todos los pesos y desplazamientos). Luego cambiamos la regla de actualización de descenso de gradiente w → w ′ = w - η∇C a

$$

$$v \rightarrow v' = \mu v - \eta \nabla C \tag{107}$$

$$

$$w \rightarrow w' = w+v' \tag{108}$$

En ecuaciones, μ es un hiperparámetro que controla la cantidad de frenado o fricción del sistema. Para comprender el significado de las ecuaciones, primero es útil considerar el caso en el que μ = 1, es decir, cuando no hay fricción. En este caso, el estudio de las ecuaciones muestra que ahora la "fuerza" ∇C cambia la velocidad v, y la velocidad controla la velocidad de cambio w. Intuitivamente, se puede ganar velocidad agregando constantemente miembros de gradiente. Esto significa que si el gradiente se mueve en aproximadamente una dirección durante varias etapas de entrenamiento, podemos obtener una velocidad de movimiento suficientemente alta en esta dirección. Imagine, por ejemplo, lo que sucede al descender:



Con cada paso hacia abajo, la velocidad aumenta, y nos movemos cada vez más rápido al fondo del valle. Esto permite que la técnica de velocidad funcione mucho más rápido que el descenso de gradiente estándar. Por supuesto, el problema es que, habiendo llegado al fondo del valle, nos deslizaremos por él. O, si el gradiente cambia demasiado rápido, podría resultar que nos estamos moviendo en la dirección opuesta. Este es el punto de introducir el hiperparámetro μ en (107). Dije anteriormente que μ controla la cantidad de fricción en el sistema; más precisamente, la cantidad de fricción debe ser imaginada como 1-μ. Cuando μ = 1, como vimos, no hay fricción, y la velocidad está completamente determinada por el gradiente ∇C. Y viceversa, cuando μ = 0, hay mucha fricción, no se gana velocidad y las ecuaciones (107) y (108) se reducen a las ecuaciones de descenso de gradiente habituales, w → w ′ = w - η∇C. En la práctica,El uso del valor de μ en el intervalo entre 0 y 1 nos puede dar la ventaja de la capacidad de ganar velocidad sin peligro de deslizarnos al mínimo. Podemos seleccionar dicho valor para μ utilizando los datos de confirmación pendientes de la misma manera que elegimos los valores para η y λ.

Hasta ahora he evitado nombrar el hiperparámetro μ. El hecho es que el nombre estándar para μ fue mal elegido: se llama coeficiente de impulso. Esto puede ser confuso porque μ no se parece en nada al concepto de impulso de la física. Está mucho más fuertemente asociado con la fricción. Sin embargo, el término "coeficiente de impulso" se usa ampliamente, por lo que continuaremos usándolo también.

Una buena característica de la técnica de impulso es que no se necesita hacer casi nada para cambiar la implementación del descenso de gradiente para incluir esta técnica en ella. Todavía podemos usar la propagación hacia atrás para calcular gradientes, como antes, y usar ideas como verificar minipacks seleccionados estocásticamente. En este caso, podemos obtener algunos de los beneficios de la optimización de Hesse utilizando información sobre los cambios de gradiente. Sin embargo, todo esto sucede sin fallas y solo con cambios menores en el código. En la práctica, la técnica de impulso se usa ampliamente y a menudo ayuda a acelerar el aprendizaje.

Ejercicios

• ¿Qué saldrá mal si usamos μ> 1 en la técnica de pulso?
• ¿Qué saldrá mal si usamos μ <0 en la técnica de pulso?

Desafío

• Agregue un descenso de gradiente estocástico basado en el impulso a network2.py.

Otros enfoques para minimizar la función de costos

Se han desarrollado muchos otros enfoques para minimizar la función de costos, y no se ha llegado a un acuerdo sobre el mejor enfoque. Profundizando en el tema de las redes neuronales, es útil profundizar en otras tecnologías, comprender cómo funcionan, cuáles son sus fortalezas y debilidades, y cómo ponerlas en práctica. En el trabajo que mencioné anteriormente , se introducen y comparan varias de estas técnicas, incluido el descenso de gradiente emparejado y el método BFGS (y también estudian el método BFGS estrechamente relacionado con la restricción de memoria, o L-BFGS ). Otra tecnología que recientemente ha mostrado resultados prometedores., este es el gradiente acelerado de Nesterov, que mejora la técnica del pulso. Sin embargo, el descenso de gradiente simple funciona bien para muchas tareas, especialmente cuando se usa el impulso, por lo que nos quedaremos con el descenso de gradiente estocástico hasta el final del libro.

Otros modelos de neurona artificial

Hasta ahora, hemos creado nuestro NS utilizando neuronas sigmoideas. En principio, el NS construido sobre neuronas sigmoideas puede calcular cualquier función. Pero en la práctica, las redes construidas en otros modelos de neuronas a veces están por delante de las sigmoideas. Dependiendo de la aplicación, las redes basadas en dichos modelos alternativos pueden aprender más rápido, generalizarse mejor a los datos de verificación o hacer ambas cosas. Permítanme mencionar un par de modelos alternativos de neuronas para darle una idea de algunas opciones de uso común.

Quizás la variación más simple sería una neurona tang que reemplaza una función sigmoidea con una tangente hiperbólica. La salida de una neurona tang con entrada x, un vector de pesos w, y un desplazamiento b se especifica como

$$

$$\tanh(w \cdot x+b) \tag{109}$$

donde tanh es tangente hiperbólica natural . Resulta que está muy conectado con la neurona sigmoidea. Para ver esto, recuerde que tanh se define como

$$

$$\tanh(z) \equiv \frac{e^z-e^{-z}}{e^z+e^{-z}} \tag{110}$$

Usando un poco de álgebra, es fácil ver que

$$

$$\sigma(z) = \frac{1+\tanh(z/2)}{2} \tag{111}$$

es decir, tanh solo está escalando el sigmoide. Gráficamente, también puede ver que la función tanh tiene la misma forma que la sigmoidea: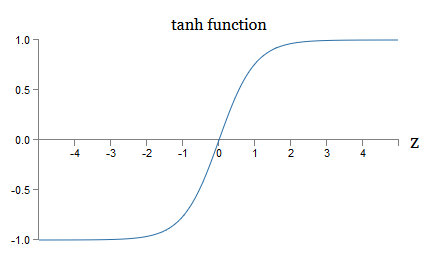



una diferencia entre las neuronas tang y las neuronas sigmoideas es que la salida de la primera se extiende de -1 a 1, y no de 0 a 1. Esto significa que al crear una red basada en neuronas tang, es posible que deba normalizar sus salidas (y, dependiendo de los detalles de la aplicación, quizás las entradas) de forma un poco diferente que en las redes sigmoideas.

Al igual que las sigmoideas, las neuronas tang, en principio, pueden calcular cualquier función (aunque hay algunos trucos), marcando entradas de -1 a 1. Además, las ideas de propagación hacia atrás y descenso de gradiente estocástico son tan fáciles de aplicar a tang -neuronas, así como a sigmoides.

Ejercicio

• Demuestre la ecuación (111).

¿Qué tipo de neurona se debe usar en redes, tang o sigmoide? ¡La respuesta, por decirlo suavemente, no es obvia! Sin embargo, existen argumentos teóricos y alguna evidencia empírica de que las neuronas tang a veces funcionan mejor. Repasemos brevemente uno de los argumentos teóricos a favor de las neuronas tang. Supongamos que usamos neuronas sigmoides, y todas las activaciones en la red serán positivas. Considere los pesos w ^{l + 1} _jk incluidos para la neurona No. j en la capa No. l + 1. Las reglas de retropropagación (BP4) nos dicen que el gradiente asociado con esto será igual a ^l _k δ ^{l + 1} _j . Como las activaciones son positivas, el signo de este gradiente será el mismo que el de δ ^{l + 1} _j. Esto significa que si δ ^{l + 1} _{j es} positivo, entonces todos los pesos w ^{l + 1} _jk disminuirán durante el descenso del gradiente, y si δ ^{l + 1} _{j es} negativo, entonces todos los pesos w ^{l + 1} _jkaumentará durante el descenso del gradiente. En otras palabras, todos los pesos asociados con la misma neurona aumentarán o disminuirán juntos. Y esto es un problema, porque es posible que deba aumentar algunos pesos mientras reduce otros. Pero esto solo puede suceder si algunas activaciones de entrada tienen signos diferentes. Esto sugiere la necesidad de reemplazar el sigmoide con otra función de activación, por ejemplo, la tangente hiperbólica, que permite que las activaciones sean tanto positivas como negativas. De hecho, dado que tanh es simétrico con respecto a cero, tanh (−z) = −tanh (z), uno puede esperar que, en términos generales, las activaciones en capas ocultas se distribuyan por igual entre positivo y negativo. Esto ayudará a garantizar que no haya sesgos sistemáticos en las actualizaciones de las escalas en una dirección u otra.

¿Cuán seriamente debe considerarse este argumento? Después de todo, es heurístico, no proporciona evidencia estricta de que las neuronas tang sean superiores a las sigmoideas. ¿Quizás las neuronas sigmoideas tienen algunas propiedades que compensan este problema? De hecho, en muchos casos, la función de tanh mostró ventajas mínimas o nulas en comparación con la sigmoidea. Desafortunadamente, no tenemos métodos simples e implementados rápidamente para verificar qué tipo de neurona aprenderá más rápido o demostrará ser más eficaz en generalizar para un caso particular.

Otra variante de una neurona sigmoidea es una neurona lineal rectificada, o unidad lineal rectificada, ReLU. La salida ReLU con entrada x, el vector de los pesos w y el desplazamiento b se especifica de la siguiente manera:

$$

$$\max(0, w \cdot x+b) \tag{112}$$

La función de enderezamiento gráfico max (0, z) se ve así:



tales neuronas, obviamente, son muy diferentes de las neuronas sigmoideas y tang. Sin embargo, son similares en que también se pueden usar para calcular cualquier función, y se pueden entrenar usando la propagación hacia atrás y el descenso de gradiente estocástico.

¿Cuándo debo usar ReLU en lugar de neuronas sigmoides o tang? En trabajos recientes sobre reconocimiento de imágenes ( 1 , 2 , 3 , 4) Se encontraron serias ventajas de usar ReLU en casi toda la red. Sin embargo, al igual que con las neuronas tang, todavía no tenemos una comprensión realmente profunda de cuándo exactamente qué ReLU serán preferibles y por qué. Para tener una idea de algunos problemas, recuerde que las neuronas sigmoideas dejan de aprender cuando están saturadas, es decir, cuando la salida está cerca de 0 o 1. Como hemos visto muchas veces en este capítulo, el problema es que los miembros σ 'reducen el gradiente eso ralentiza el aprendizaje. Las neuronas Tang sufren dificultades similares en la saturación. Al mismo tiempo, un aumento en la entrada ponderada en ReLU nunca lo saturará, por lo tanto, no se producirá una desaceleración correspondiente en el entrenamiento. Por otro lado, cuando la entrada ponderada en el ReLU es negativa, el gradiente desaparece y la neurona deja de aprender.Estos son solo algunos de los muchos problemas que hacen que no sea trivial entender cuándo y cómo las ReLU se comportan mejor que las neuronas sigmoideas o tangibles.

Pinté una imagen de incertidumbre, enfatizando que todavía no tenemos una teoría sólida de la elección de las funciones de activación. De hecho, este problema es aún más complicado de lo que describí, ya que hay infinitas funciones de activación posibles. ¿Cuál nos dará la red de aprendizaje más rápido? ¿Cuál dará la mayor precisión en las pruebas? Me sorprende cuán pocos estudios realmente profundos y sistemáticos han sido sobre estos temas. Idealmente, deberíamos tener una teoría que nos diga en detalle cómo elegir (y posiblemente cambiar sobre la marcha) nuestras funciones de activación. Por otro lado, ¡no deberíamos detenernos por la falta de una teoría completa! Ya tenemos herramientas poderosas, y con su ayuda podemos lograr un progreso significativo. Hasta el final del libro usaré las neuronas sigmoideas como las principales,ya que funcionan bien y dan ilustraciones concretas de ideas clave relacionadas con la Asamblea Nacional. Pero tenga en cuenta que las mismas ideas se pueden aplicar a otras neuronas, y estas opciones tienen sus ventajas.

: , , ? ?

: , . , . . : , , ?

—

Una vez en una conferencia sobre los conceptos básicos de la mecánica cuántica, noté algo que parecía un hábito gracioso: al final del informe, las preguntas de la audiencia a menudo comenzaron con la frase: "Realmente me gusta tu punto de vista, pero ..." Los fundamentos cuánticos no son mi campo habitual, y llamé la atención sobre este estilo de hacer preguntas porque en otras conferencias científicas prácticamente no me reuní con el interlocutor para mostrar simpatía por el punto de vista del hablante. En ese momento, decidí que la prevalencia de tales preguntas indicaba que el progreso en los fundamentos cuánticos se había logrado bastante y que las personas apenas comenzaban a ganar impulso. Más tarde me di cuenta de que esta evaluación era demasiado dura. Los oradores lucharon con algunos de los problemas más difíciles que las mentes humanas han encontrado. ¡Naturalmente, el progreso fue lento!Sin embargo, todavía valía la pena escuchar las noticias de las personas que pensaban en esta área, incluso si tenían poco o nada.

En este libro puede haber notado una "marca nerviosa" similar a la frase "Estoy muy impresionado". Para explicar lo que tenemos, a menudo recurrí a palabras como "heurísticamente" o "más o menos hablando", seguido de una explicación de un fenómeno particular. Estas historias son creíbles, pero la evidencia empírica fue a menudo bastante superficial. Si estudia la literatura de investigación, verá que historias de este tipo aparecen en muchos trabajos de investigación sobre redes neuronales, a menudo en compañía de una pequeña cantidad de evidencia que los respalda. ¿Cómo nos relacionamos con tales historias?

En muchos campos de la ciencia, especialmente donde se consideran fenómenos simples, uno puede encontrar evidencia muy estricta y confiable de hipótesis muy generales. Pero en la Asamblea Nacional hay una gran cantidad de parámetros e hiperparámetros, y hay relaciones extremadamente complejas entre ellos. En sistemas tan increíblemente complejos, es increíblemente difícil hacer declaraciones generales confiables. La comprensión del NS en toda su plenitud, como los fundamentos cuánticos, pone a prueba los límites de la mente humana. A menudo tenemos que prescindir de la evidencia a favor o en contra de varios casos particulares específicos de una declaración general. Como resultado, a veces es necesario cambiar o abandonar estas declaraciones, a medida que surgen nuevas pruebas.

Uno de los enfoques para esta situación es considerar que cualquier historia heurística sobre el NS implica un cierto desafío. Por ejemplo, considere la explicación que cité sobre por qué funciona una excepción (abandono) del trabajo en 2012.: “Esta técnica reduce la compleja adaptación articular de las neuronas, ya que una neurona no puede confiar en la presencia de ciertos vecinos. Al final, tiene que aprender rasgos más confiables que pueden ser útiles para trabajar junto con muchos subconjuntos aleatorios diferentes de neuronas ". Una declaración rica y provocativa, sobre la base de la cual puede construir un programa de investigación completo, en el que necesitará descubrir qué es verdad, dónde está mal y qué debe aclararse y modificarse. Y ahora realmente hay toda una industria de investigadores que estudian la excepción (y sus muchas variaciones), tratando de entender cómo funciona y qué limitaciones tiene. Así es con muchos otros enfoques heurísticos que discutimos. Cada uno de ellos no es solo una explicación potencial,pero también un desafío para la investigación y una comprensión más detallada.

Por supuesto, ninguna persona tendrá tiempo suficiente para investigar todas estas explicaciones heurísticas con suficiente profundidad. Toda la comunidad de investigadores de NS tardará décadas en desarrollar una teoría realmente poderosa del entrenamiento de NS basada en la evidencia. ¿Significa esto que vale la pena rechazar las explicaciones heurísticas como pruebas laxas y carentes de evidencia? No!Necesitamos una heurística que inspire nuestro pensamiento. Esto es similar a la era de los grandes descubrimientos geográficos: los primeros estudiosos a menudo actuaban (e hicieron descubrimientos) basándose en creencias que se equivocaron de manera seria. Más tarde, corregimos estos errores, reponiendo nuestro conocimiento geográfico. Cuando comprendes algo mal, como los investigadores entendieron la geografía, y como entendemos hoy el NS, es más importante estudiar audazmente lo desconocido que estar escrupulosamente en cada paso de tu razonamiento. Por lo tanto, debe considerar estas historias como instrucciones útiles sobre cómo reflexionar sobre las NS, manteniendo una conciencia saludable de sus limitaciones y monitoreando cuidadosamente la confiabilidad de la evidencia en cada caso. En otras palabras, necesitamos buenas historias para motivarnos e inspirarnos, e investigaciones minuciosas y escrupulosas, a fin depara descubrir hechos reales.