Vine al mundo de las TI desde la física teórica. Se dedicaba principalmente a tareas económicas. Comprometido: esto: análisis, conocimientos tradicionales, declaración, diseño, programación. Naturalmente, todo el tiempo comparé los enfoques físicos y económicos para comprender las leyes de la naturaleza y la economía, respectivamente. Un cierto punto de vista ha madurado sobre este tema. Sobre ella y será discutido.
1. Sobre la cognición en general
Hay dos enfoques para la cognición:
El enfoque de Aristóteles . Este es un enfoque holístico y trata el objeto como un cuadro negro. El fenómeno, el objeto se estudia en toda realidad como un todo. Y la realidad dice, por ejemplo, que los cuerpos pesados caen al suelo más rápido que los ligeros; eso dejó solo un cuerpo en movimiento que se detiene gradualmente. El enfoque de Aristóteles trata el fenómeno como una realidad integral, por lo tanto, puede llamarse fenomenológico.
El enfoque de Galileo . Este es un enfoque analítico de sistemas. Este es el enfoque de divide y vencerás. El fenómeno, el objeto se descompone en sus partes constituyentes y cada uno de ellos se estudia por separado, abstrayéndose del resto (análisis). Luego, las imágenes resultantes se pueden combinar en una sola, teniendo en cuenta la interacción de los componentes (síntesis). Por ejemplo, la caída de cuerpos se considera como la caída de cuerpos en el vacío. Y allí resultan caer con la misma aceleración. Pero en realidad, la fricción contra el aire les impide caer por igual. Habiendo estudiado esta fuerza por separado, podemos explicar el resultado de Aristóteles. Del mismo modo, si nos desconectamos de las fuerzas de fricción, el cuerpo en movimiento se moverá sin detenerse. Y si tenemos en cuenta la fuerza de fricción, obtenemos el resultado de Aristóteles. El enfoque de Galileo lleva inmediatamente a la necesidad de estudiar las fuerzas. Esto, al final, se traduce en un sistema coherente de física clásica.
Una vez más, para mayor claridad.
El enfoque de Aristóteles . Hay un fenómeno en estudio, "La caída de un cuerpo en el aire al suelo", el fenómeno F. Tomamos diferentes cuerpos y encontramos que los cuerpos más pesados caen al suelo más rápido que los ligeros.
El enfoque de Galileo . Al estudiar el fenómeno de F, se debe tener en cuenta no solo el peso. Estudiamos la caída en el aire. Y cambiemos no solo el peso, sino también el aire. Tratemos de reducir su densidad, de modo que, al final, no haya aire. Luego encontramos que todos los cuerpos caen en el vacío con la misma aceleración. Encontramos los parámetros de influencia en el fenómeno e intentamos crear condiciones bajo las cuales solo un parámetro sea significativo. Esto no está en la naturaleza. Por lo tanto, un físico necesita un laboratorio donde pueda variar los parámetros. Habiendo estudiado la influencia de un parámetro, podemos proceder a estudiar la influencia de otro parámetro. Estamos tratando de reducir la complejidad de todo el enfoque para la composición de enfoques más simples. Variando la forma del cuerpo que cae, podemos estudiar la dependencia de la fuerza de fricción sobre el aire dependiendo de la forma del cuerpo. Al variar la velocidad de caída, podemos detectar la dependencia de la fuerza de fricción en la velocidad. Al variar la altura de la caída, podemos detectar la dependencia de la aceleración de la altura. Al variar la ubicación geográfica en la tierra, encontramos la dependencia de la aceleración de la caída en la geografía.
Hablando en términos generales, en el enfoque de Aristóteles estudian la realidad, y en el enfoque de Galileo estudian las abstracciones, y de ellos, a través de la síntesis, van a la realidad.
2. El modelo del conocimiento físico.
La física es una teoría ideal para muchas ciencias, incluida la economía. En experimentos físicos, se obtienen series discretas de valores. Pero se consideran una aproximación a las funciones continuas, que en realidad son indicadores físicos. Y los físicos están tratando de adivinar estas funciones. De modo que Galileo adivinó la parábola por la trayectoria de una piedra lanzada en ángulo hacia el horizonte; Kepler adivinó las trayectorias de los planetas: elipses, etc. Habiendo adivinado la trayectoria, obtenemos un aparato predictivo: la capacidad de calcular el valor de coordenadas inexploradas de la trayectoria. Para probar, ponen un experimento: crean las condiciones para obtener experimentalmente el valor de interés. Luego, habiendo verificado el valor predicho y el valor experimental, obtenemos confirmación o refutación de la teoría. Aquí a veces el error del error experimental juega un papel importante. El conocimiento físico se reduce a la identificación del determinismo: la ley de obtener un estado a partir de un estado inicial:
S(0) - D – – , S(t) S(0) Q – . , , .
Entonces, para una piedra lanzada desde un punto (0,0) con una velocidad en ángulo hasta el horizonte tenemos
$$ display $$ x (t) = v_0 t cos (α), y (t) = v_0 t sin (α) - (gt ^ 2) / 2 $$ display $$
El estado inicial S (0) se establece mediante tres parámetros: punto de partida (0,0), velocidad inicial ángulo .
El impacto del medio ambiente Q viene dado por la aceleración de la gravedad g. Al expandir el alcance del problema (alta velocidad inicial) g ya no es constante.
El determinismo D viene dado por la fórmula anterior.
Para una tarea más realista, se debe tener en cuenta la fricción contra el aire. Esto complica la matemática del problema, pero el principio sigue siendo el mismo. En lugar de piedra, puede considerar un avión. Luego entra en juego la fuerza de empuje del avión y su regulación por parte del piloto. También aparece un factor no físico: la voluntad del piloto. No podemos tenerlo en cuenta. Pero sabemos que no es ilimitado: la tracción no puede ser infinita, la aceleración no puede ser infinita. Esto introduce un elemento de certeza en el movimiento. Lo usan, por ejemplo, para construir la trayectoria de un misil de defensa aérea.
Volvamos a la piedra voladora. Se caracteriza por un número infinito de parámetros físicos. Por ejemplo, solo su forma puede ser arbitrariamente compleja. Pero estamos seguros de que en algún área útil podemos considerar la piedra como un punto material. Esta es la principal abstracción de la mecánica clásica. Todos los sistemas se representan como conjuntos de puntos de material que interactúan. Esto constituye la principal reducción cognitiva: reducir el comportamiento de un sistema complejo al comportamiento de sus componentes elementales.
En relación con la reducción cognitiva mencionada, se pueden distinguir dos enfoques epistemológicos: reduccionismo y holismo.
3. Reduccionismo y holismo.
El reduccionismo es el principio de reducir las características de un sistema de las características de los subsistemas y las características de la interacción de los subsistemas. Trabaja exitosamente en física.
Considere, por ejemplo, el gas. Sin descomponerlo en subsistemas, podemos operar con conceptos experimentales y fenomenológicos: presión P, temperatura T, volumen V. Empíricamente, encontramos la relación que conecta estos parámetros: la ecuación de estado del gas:
Este es el llamado nivel fenomenológico: trabajar con fenómenos (fenómenos) sin entrar en su estructura. Este es el enfoque de Aristóteles.
Ahora aplique el enfoque de Galileo. Descomponemos el sistema de "gas": imagínelo como una colección de moléculas en colisión. Luego definimos P y T a través de los parámetros mecánicos de la molécula. Esto se hace en física molecular. Por lo tanto, reducimos el sistema de gas a subsistemas de moléculas. Esto aclarará la ecuación de estado o la deducirá para nuevos sistemas.
En consecuencia, en los negocios tenemos una analogía: la macroeconomía se descompone en empresas y hogares. Pero aquí la reducción aún no es perfecta. Por desgracia, no hay Newton económico. El problema es la complejidad y la disponibilidad de un factor subjetivo que no está en la física (aunque existe un debate sobre el papel del sujeto en la mecánica cuántica).
Y ahora sobre el holismo.
El holismo es el principio de que puede haber propiedades no reducibles en un sistema. Entonces, en biología, la doctrina del vitalismo se basa en el concepto de entelequia, la fuerza vital inherente al cuerpo como un todo e irreductible.
La física hasta ahora prescinde del concepto de holismo.
Un modelo de fórmula es un modelo definido por una fórmula. El concepto de "fórmula" se considerará conocido.
Ejemplos en física: ecuaciones de Newton, ecuaciones de Lagrange, ecuaciones de Maxwell, ecuaciones de Navier-Stokes, ecuaciones de Heisenberg-Schrödinger, ecuaciones de Einstein.
Ejemplos de la economía: fórmula de Black-Scholes para el precio de la opción, fórmula de oferta de dinero, modelo de programación lineal para optimizar la cartera financiera, fórmulas de cálculo de intereses, fórmulas de cálculo de riesgo.
Con un modelo de fórmula, una persona puede trabajar sin una computadora. Tal es casi todo matemática pura. Pero aquí, algorítmico juega un papel cada vez más importante. Por lo tanto, la solución al problema de los cuatro colores no se redujo a ninguna fórmula, sino que requirió una solución de fuerza bruta para muchos casos especiales. Este busto fue hecho por computadoras.
Modelo algorítmico : un modelo definido por un algoritmo, posiblemente no reducible a una fórmula. Por supuesto, es posible clasificar el algoritmo como fórmulas, pero estas no son las mismas fórmulas clásicas. El modelo algorítmico es inicialmente realista solo usando una computadora
Un modelo formal siempre se puede reducir a uno algorítmico.
Un ejemplo del primer modelo algorítmico es el problema de Fermi-Pasta-Ulam. Aquí hay una cita del libro de Ulam, Las aventuras de las matemáticas.
CitaTan pronto como se completaron las máquinas, Fermi, con su intuición y gran sentido común, se dio cuenta de inmediato de toda su importancia en el estudio de problemas de física teórica, astrofísica y física clásica. Discutimos este tema de la manera más detallada y decidimos tratar de formular algún problema que fuera simple en su formulación, pero que tuviera una solución que requiriera cálculos muy largos, imposible con la ayuda de un bolígrafo y papel o dispositivos de computación mecánica existentes. Tras analizar una serie de posibles problemas, decidimos un problema típico relacionado con el comportamiento a largo plazo de un sistema dinámico y que requiere una predicción a largo plazo. Consideró una cuerda elástica con dos extremos fijos, que se ve afectada no solo por la fuerza de deformación elástica habitual proporcional a la deformación, sino también por una pequeña fuerza física no lineal. Era necesario descubrir cómo, después de un gran número de períodos de oscilaciones, esta no linealidad afectará gradualmente el comportamiento periódico conocido de las oscilaciones en una tecla, cómo otras teclas clave adquirirán sus amplitudes y cómo, razonamos, el movimiento se térmicoizará, imitando, tal vez, el comportamiento líquidos, que, siendo inicialmente laminar, se vuelven cada vez más turbulentos, hasta que, finalmente, su movimiento macroscópico se convierte en calor.
John Pasta, un físico que llegó recientemente a Los Alamos, nos ayudó a crear diagramas de flujo, programación y tareas de procesamiento en MANIAC. Fermi decidió aprender a programar una máquina. En aquellos días, era más difícil de hacer que ahora, cuando ya existen programas listos y reglas establecidas, y este procedimiento en sí mismo está automatizado. Entonces fue necesario aprender varios trucos. Fermi los dominó muy rápidamente y me enseñó algo, aunque ya sabía lo suficiente como para poder evaluar qué tipo de tareas se pueden resolver de esta manera, determinar su duración en la cantidad de pasos de cálculo y comprender los principios de su implementación.
Al final resultó que, seleccionamos con éxito la tarea. Los resultados obtenidos en términos cualitativos diferían completamente incluso de los que Fermi esperaba con su conocimiento más profundo de los movimientos de onda. El objetivo inicial era ver a qué velocidad la energía de la cuerda, originalmente incrustada en una onda sinusoidal simple (se tomó una nota como un solo tono), crearía gradualmente armónicos más altos y cómo el sistema llegaría a un estado caótico final, describiendo cómo la forma de la cuerda , por lo que la naturaleza de la distribución de energía entre claves superiores y superiores. Pero nada de eso sucedió. Para nuestra sorpresa, la cuerda comenzó a tocar solo en unas pocas notas sordas y, lo que probablemente sea aún más sorprendente, después de varios cientos de vibraciones recíprocas ordinarias, nuevamente tomó casi la misma forma sinusoidal que al principio.
Sé que Fermi consideró esto como un "descubrimiento menor", como él mismo dijo. Pero iba a contar sobre él un año después, cuando Gibbs lo invitó a dar una conferencia (un evento muy honorable en la reunión anual de la American Mathematical Society). Cayó enfermo antes de la reunión, y esta conferencia nunca tuvo lugar. Sin embargo, se publicó un informe sobre este trabajo, escrito por Fermi, Pasta y yo, como un informe sobre el trabajo en Los Alamos.
Debo explicar que el movimiento de un medio continuo, como una cuerda, por ejemplo, puede estudiarse usando una computadora si imaginamos que una cuerda consiste en un número finito de partículas, en nuestro caso, sesenta y cuatro o ciento veintiocho. (El número de elementos se representa mejor como una potencia de dos, ya que esto facilita el procesamiento en una computadora). Estas partículas están interconectadas por fuerzas que, además de los términos lineales de distancia, también contienen pequeños términos cuadráticos no lineales. Luego, la máquina calcula rápidamente el movimiento de cada uno de estos puntos en pasos cortos. Después de calcular una posición, pasa a otra etapa de tiempo y calcula una nueva posición, por lo que se repite muchas veces. No hay absolutamente ninguna manera de hacer este cálculo manualmente, tomaría literalmente miles de años. La solución en forma analítica utilizando métodos matemáticos de análisis clásico de los siglos XIX y XX es completamente inaceptable aquí.
Los resultados fueron realmente asombrosos. Se han hecho muchos intentos para dilucidar las causas de ese comportamiento periódico y regular, que se ha convertido en una fuente de la voluminosa literatura sobre oscilaciones no lineales que existen hoy en día. El trabajo sobre ellos fue escrito por Martin Kruskal, un físico de Princeton, y Norman Zabuski, un matemático que trabajó en el Laboratorio de Bell Telephone. Más tarde, Peter Lake hizo su brillante contribución a esta teoría. Todos ellos realizaron un interesante análisis de problemas de este tipo. El matemático sabe que el llamado sistema dinámico de retorno de Poincare, que incluye tantas partículas, tiene una longitud gigantesca, de hecho, en una escala astronómica, y que está volviendo tan rápidamente a su posición original es lo más sorprendente.
Otro físico de Los Alamos, James So, decidió ver si el período que sigue a este regreso tan cercano a la posición inicial comienza nuevamente desde el mismo estado, y qué sucederá después de este segundo "período". Junto con Pasta y Metrópolis, repitió todo el procedimiento y, sorprendentemente, el retorno se produjo nuevamente, pero con una precisión de menos del uno por ciento. Esta imagen se repitió aún más, pero después de seis o doce de esos períodos, la precisión comenzó a aumentar nuevamente, lo que indicaba la aparición de un cierto "súper período". Entonces, una extrañeza fue seguida por otra, nada menos.
Y aquí hay un artículo sobre Habré, que habla sobre el estado actual del problema de Fermi-Pasta-Ulam:
Los matemáticos resolvieron el problema de Fermi-Pasta-Ulam
5. Coordinación
Por coordinación del sistema, me refiero a la definición de parámetros básicos que, en principio, determinan la evolución del sistema. Por ejemplo, en la mecánica de un punto material, la coordinación se define por:
- Fuerza externa F
- Masa m punto material
- Coordenadas espaciales (x, y, z) = r del punto material
- Tiempo t
La evolución del sistema viene dada por la ecuación de Newton.
¿Cuál es la coordinación de la entidad económica? Una vez trabajé en un sistema de inteligencia empresarial. Su término principal es indicador. La base del sistema es un cuadro de mando. Cientos de indicadores. Pero busqué en vano en Internet una descripción de la base de los indicadores: un conjunto de indicadores que no pueden reducirse a otros y que, en principio, determinan por completo la evolución de una entidad económica. Es decir, según tengo entendido, no se ha realizado ninguna coordinación en la economía. Y, por lo tanto, hablar sobre alguna ley dinámica básica aún no es posible. Solo es posible, basado en la conexión de indicadores, realizar un análisis de escenarios: responder a la pregunta "¿Qué pasará con los indicadores derivados si los indicadores subyacentes cambian de acuerdo con el escenario dado?"
6. Ejemplo abstracto. Predicción de series temporales como la física
Puede preguntar el problema de pronóstico basado en la serie de tiempo real: al tener varios valores reales, necesita obtener el valor pronosticado del indicador, el valor en el futuro. Esto implica una especie de determinismo oculto de la serie temporal. Hubo muchas especulaciones científicas y pseudocientíficas sobre este tema. Yo mismo traté con doctores en ciencias que afirmaron que su metodología les permitiría obtener un pronóstico del tipo de cambio y mostré las disertaciones correspondientes con todo tipo de intervalos de confianza y otros atributos de las leyes de distribución. Pero, cuando se enfrentan a la realidad, las técnicas quedaron impresionadas.
A veces, para obtener un pronóstico, haga esto:
- Tome la serie en tiempo real {V (ti)}. Horario: línea discontinua escalonada.
- Tome una función continua W (t) tal que W (ti) = V (ti). El gráfico es una curva continua.
- Se selecciona un polinomio P (t) que se aproxima a W (t) con un grado suficiente de precisión. Se puede considerar un polinomio para todas las t.
- Entonces tenemos un pronóstico para el tiempo futuro T: V (T) = P (T)
Todo esto da la impresión de ciencia, pero solo a primera vista. Sí, la existencia de un polinomio aproximado para W (t) está garantizada por el teorema de Weierstrass del matanálisis. Podemos polinomizar arbitrariamente con precisión W (t). Pero no se puede usar para predicciones.
El valor aproximado para la serie real es 100%, y el valor predictivo es cero. Los polinomios se pueden inventar arbitrariamente, pero todos darán pronósticos diferentes.
Cuando llega el día T y descubrimos la V (T) real, entonces para la serie {{V (ti)}, V (T)} podemos construir un nuevo polinomio Q (t) que se aproxima a esta serie arbitrariamente con precisión, pero el tiempo T ya no está en el futuro y Q (T) ya no es un pronóstico, sino una realidad. Los polinomios P (t) y Q (t) no tienen que coincidir absolutamente y para el nuevo tiempo de pronóstico T '> T mostrarán resultados diferentes. Es decir, no hay pronóstico. Parece que hay ciencia, pero no hay pronóstico. Es como una teoría medieval de los ángeles. Ella puede explicar todo, pero no puede predecir nada.
La diferencia entre interpolación física y extrapolación económica:
- La precisión de los datos empíricos : aproximada en física, precisa en economía
- Funciones de dominio : continua en física, discontinua, gradual en economía
- Datos empíricos : en física, discreta, en economía continua con discontinuidades discretas
- Leyes básicas : en física allí. F = ma, por ejemplo; en la economía todavía
7. Economía y física.
En economía, las trayectorias reales, esencialmente discontinuas, son funciones constantes por partes. Por ejemplo, el indicador "Tipo de cambio" puede dar un salto en cualquier momento. Funciones económicas continuas: aproximaciones en aras del matanálisis (si tiene un martillo en las manos, entonces desea considerar cualquier objeto como un clavo ...). Cada transacción contable provoca saltos en los valores de los indicadores de derivados de las cuentas. Y son la mayoría de los indicadores. Además, cada cambio en el número de trabajadores es discreto, etc. La continuidad de las trayectorias económicas contrasta con la continuidad de la mayoría de las trayectorias físicas. Por lo tanto, el aparato de matanálisis no es directamente aplicable a las trayectorias económicas.
Imagen para la cognición física. La trayectoria de una piedra arrojada en ángulo al horizonte 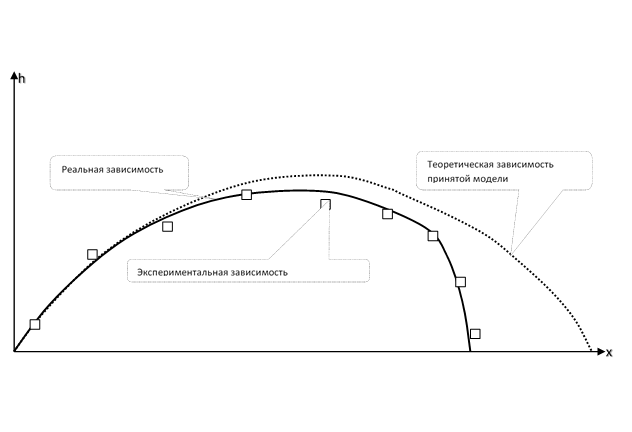
Cuadro para el conocimiento económico. Tipo de cambio de moneda en el banco central.

Esta es una función exacta experimental real. Es discontinuo en momentos en que el tipo de cambio cambia.
En física:
- Los valores físicos experimentales son casi siempre aproximados.
- Los valores físicos experimentales forman una serie discreta.
- Una serie discreta experimental se considera como un polígono para la aproximación continua porque la realidad es continua. La noción de continuidad puede llegar a ser una mentira en pequeñas escalas espaciales y temporales. Entonces la física cambiará su cara.
- Indicadores de referencia bien definidos
- Las trayectorias teóricas y reales son casi siempre continuas y casi siempre diferenciables (la trayectoria de un punto material siempre es dos veces diferenciable en el tiempo)
- Debido a la continuidad de la dinámica real y la trayectoria real, su buena aproximación continua tiene poder predictivo: en un vecindario suficientemente pequeño, la función no se alejará de su último valor real.
En la economia:
- Los valores económicos experimentales pueden considerarse exactos. Solo en macroeconomía hay un problema de precisión debido a la gran cantidad de entidades comerciales.
- Los valores económicos experimentales consisten en intervalos de constancia, interrumpidos en ciertos puntos en el tiempo cuando el valor cambia abruptamente
- Los datos experimentales no pueden considerarse como un campo de pruebas para la aproximación continua porque la realidad es discontinua.
- Indicadores de referencia no completamente definidos. No está claro por qué bailar.
- Debido a la discontinuidad de la trayectoria real, cualquier aproximación continua arbitrariamente buena no garantiza predicciones en ningún vecindario arbitrariamente pequeño.
- Las trayectorias reales son casi siempre discontinuas. Esto significa que la determinación económica requiere un enfoque diferente de la mecánica clásica.
- En la economía, inicialmente hay un factor de libre albedrío de una entidad económica. Su rango está regulado por el estado. Los límites extremos de esta libertad:
- Libertad total en un mercado no regulado por el estado
- Libertad parcial en un mercado parcialmente regulado por el estado
- Completa falta de libertad en un estado totalmente centralizado donde no hay libre mercado
El conocimiento económico no ha alcanzado un nivel similar a la mecánica clásica:
- Los componentes elementales del tipo de punto material no están definidos.
- Q no definido (parámetros ambientales), no está claro qué es importante, qué no es importante,
- ,
- ; .
. – . – . ? , . . . . , – .
, . , , - .
8. IT
8.1.
. . . . , . . . . . . . , , . . … , . . , . . . , . . . De la mano . . . . . . . – " . - "!? , . -1840( , ). . . , . , . , . , . . , , . (). . , , , : ", . ". ! . , , - .
8.2. -
. — . , , .. . . , . . – . , . , . – . . …
. . , . , , , . , . . . . . , - . . . . , : , . . . , , . . ? . . , .
. - , .
, , . , . . , .
. . . , . , . , : , . , . . .
, – Jump Processing. , . .
, . “ ”. , – . , , . – , . . , – .
8.3.
( ). . “”. . , . , . . – . . , . . . . , . . – . . , . … . ? , . , - . . . , . , , . . .
. , . , . , – . , . , – ( – ?).
8.4.
“ ”
. () . . . , , . . , . . , , . . . – . , , . , . . , . . . – . , . – . . , (, ). , . . , . . , , , . . . – . . . . . . . . . : , , , , , , , , … . 100 . ( , , ) . , ( , (SQL-) ). , . Es decir . . . , . . , : ”, . . . ”.
. , . , . : . , , .
. . . , , . . . . -.
() . , , ( ), . , . , – . , , , , , . . . , , . , “” “”. , “” “”. ? , .
: . . . , . . . . — . . : . : , …
. . , . . .
Resumen
, . . - . . — . ¿Por qué es esto? .
: IT. .