Procedemos al cálculo de funciones lógicas de acuerdo con el gráfico para una clase más amplia de comportamientos. Consideramos comportamientos autónomos cíclicos que no contienen múltiples señales (o de otra manera: no contienen eventos indexados). Otra limitación: por conveniencia, no consideraremos la conexión de ramas paralelas en OR. Consideramos solo una conexión por AND, es decir, un evento se activa solo cuando se activan todos sus eventos predecesores.
Usaremos STG para describir el comportamiento, pero con restricciones adicionales. Para cada lugar, el número de arcos que entran y salen es estrictamente igual a uno cada uno. En consecuencia, un lugar con arcos entrantes y salientes puede considerarse como un arco que conecta dos eventos (transiciones). En consecuencia, la marca se mueve a lo largo de los arcos. Dado que los comportamientos con múltiples señales no se consideran ahora, los índices de eventos están prohibidos, no son necesarios. Los eventos vacíos están prohibidos. La situación también está prohibida cuando dos arcos incluidos en un evento surgen de eventos que no son paralelos entre sí (un caso especial es del mismo evento). El propósito de esto es deshacerse de los arcos que no llevan una carga semántica. El resto se considera correcto (normal, en vivo, seguro) desde el punto de vista del comportamiento de STG, teniendo en cuenta las limitaciones anteriores. El comportamiento no contiene conflictos CSC.
Definición 1. El evento en el que entra el arco es una consecuencia del evento del cual sale este arco. Por el contrario, el evento del cual sale el arco es la causa del evento en el que entra este arco.
Definición 2. Una ruta - una secuencia interminable de eventos - el resultado de cambios en el etiquetado de un gráfico, comenzando con uno específico. Cada evento ingresa a la secuencia un número infinito de veces. Cada una de esas entradas es única.
Definición 3. La traza del evento A es la ruta en la que todos los eventos son la consecuencia directa del evento A o el resultado del cierre transitivo de la relación de la consecuencia de los eventos con respecto al evento A. La marca inicial para la traza del evento A se establece de la siguiente manera. Si la marca se modifica arbitrariamente, después de que se activa el evento A, los marcadores en los arcos de salida del evento A son fijos. Luego, el resto de los marcadores se mueven hasta que el movimiento de los marcadores se vuelve imposible sin liberar los marcadores en los arcos de salida del evento A. La marca resultante es la marca inicial para la traza del evento A.
Definición 4. Introducimos la relación de ordenamiento para tres eventos (A, B, C). Se ordenan tres eventos (escritos A> B> C) si y solo si, para cualquier rastro del evento A, la primera ocurrencia del evento B en la secuencia siempre ocurrirá antes que la primera ocurrencia del evento C.
Observación El evento A puede ser paralelo a ambos eventos B y C (o solo C), o ambos eventos A y B pueden ser paralelos al evento C.
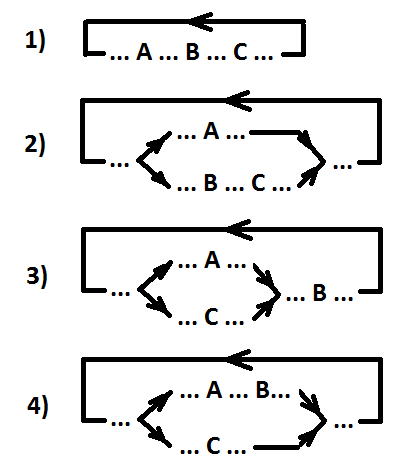
Opciones de ubicación para eventos ordenados A, B y C (A> B> C).
Definición 5. La señal b (conmutación B1 y B2) recoge la señal a (conmutación A1 y A2) con respecto a los eventos X e Y (los eventos X e Y son paralelos o coincidentes) si se cumplen las siguientes condiciones:
1) X> A1> A2;
2) si el evento A2 es paralelo al evento X y no paralelo al evento Y, entonces X> A2> Y;
3) Y> B1> B2;
4) si el evento B2 es paralelo al evento Y y no paralelo al evento X, entonces Y> B2> X;
5) Y> B1> A2;
6) si el evento A2 es paralelo al evento Y y no paralelo al evento X, entonces Y> A2> X.
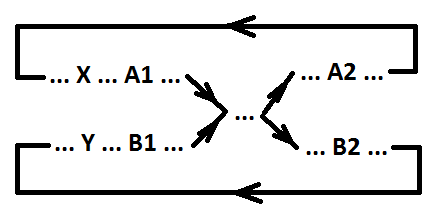
Observación 1. Las condiciones 1, 2 y 3, 4 determinan el orden de la conmutación de las señales ayb, respectivamente. Las condiciones 5, 6 especifican el orden del evento de captura B1 y el evento de captura A2.
Observación 2. El evento X puede ser el evento A1. En este caso, las condiciones 1 y 2 se degeneran.
Observación 3. El evento Y puede ser el evento B1. En este caso, las condiciones 3, 4 y 5 se degeneran.
Observación 4. El evento X puede ser el evento A1, y también el evento B1 puede ser el evento Y. En este caso, las condiciones 1, 2, 3, 4 y 5 se degeneran.
Ahora comenzamos a considerar qué es un implante. El implicante se caracteriza por eventos, como resultado de lo cual el implicante cambia su significado.
Definición 6. Un evento, como resultado de lo cual el implicante AND (OR) cambia su valor de 1 (0) a 0 (1), llamaremos el límite derecho del implicante. La señal correspondiente a este evento se llamará encendido. El implicante se enciende.
Definición 7. Un evento, como resultado de lo cual el implicante AND (OR) cambia su valor de 0 (1) a 1 (0), llamaremos al borde izquierdo del implicante. La señal correspondiente a este evento se cancelará. El implicante se apaga.
Definición 8. Un implicante en el que dos límites derechos (o dos límites izquierdos) no son paralelos entre sí se denominará discontinuo.
Por ahora, no consideraremos implantes interrumpidos. Volveremos a su consideración a continuación.
Entonces, tenemos: todos los bordes derechos de los implicados son paralelos entre sí, así como los bordes izquierdos de los implicados son paralelos entre sí.
Una propiedad importante. El implicante se enciende cuando ocurre al menos un evento, que es el borde derecho del implicante. El implicante se apaga solo cuando ocurren todos los eventos que son los límites izquierdos del implicante.
Ahora queda por identificar las propiedades de las señales que forman el implante.
Definición 9. La señal incluida en el implante se llamará variable.
La primera propiedad de las variables. Las señales de encendido y apagado son variables.
La segunda propiedad de las variables. Para cualquier variable de conmutación (uno de cuyos interruptores es el borde izquierdo del implicante L, el otro es algún evento X), debe haber un evento: algún borde derecho R del mismo implicante es tal que X y R son el mismo evento o R > X> L.
La tercera propiedad de las variables. Para cualquier variable inclusiva (uno de cuyos interruptores es el borde derecho del implicante R, el otro es algún evento X), debe haber un evento: algún borde izquierdo L del mismo implicante es tal que X y L son el mismo evento o R > X> L.
La cuarta propiedad de las variables. Para cualquier variable (cambio de X1 y X2) que no se enciende o apaga, debe haber dos eventos: un borde izquierdo del implicante L y otro borde derecho del implicante R de modo que R> X1> L y R> X2> L . De lo contrario, el implicado no podría mantener un valor constante en la posición de apagado.
La quinta propiedad de las variables. Para cualquier par: alguna variable de conmutación y otra variable de conmutación, debe haber una secuencia de variables que se recojan entre sí en relación con algunos bordes derechos del implicante (para diferentes captaciones, los bordes derechos pueden variar), comenzando con esta variable de conmutación y terminando con esta variable de conmutación . De lo contrario, el implicado no podría mantener un valor constante en la posición de encendido.
Sexta propiedad de las variables. Para cualquier variable inclusiva a, si el límite derecho del implicante es el evento a + (a-), dicha variable se incluye en el registro del implicante AND (OR) con inversión, y en el registro del implicante OR (AND) sin inversión. Para cualquier variable de conmutación a, si el borde izquierdo del implicante es el evento a- (a +), entonces esta variable a se incluye en el registro del implicante AND (OR) con inversión, y en el registro del implicante OR (AND) sin inversión.
La séptima propiedad de las variables. En virtud de la cuarta propiedad de las variables, para cada variable a que no se enciende o apaga, hay un límite derecho para los implicantes R y un borde izquierdo para los implicantes L de modo que R> a +> L y R> a-> L. Si R> a +> a-, entonces dicha variable ingresa el implicante de Y con inversión, y el implicante de OR sin inversión. Si R> a-> a +, entonces dicha variable ingresa el implicante AND sin inversión, y el implicante OR con inversión.
Las siete propiedades enumeradas de las variables son propiedades necesarias del implicante. Además, estas propiedades son suficientes para describir los implantes.
Observación La descripción anterior del implante no prohíbe la situación en la que un borde izquierdo del implante puede ser paralelo a un borde derecho del mismo implicante. El significado de este fenómeno es que, dependiendo de la velocidad de los procesos paralelos, tal implante en tiempo real puede convertirse en opcional para la implementación de la señal correspondiente y en tiempo real puede no apagarse (si el límite derecho funciona antes que el límite izquierdo).
Ahora consideraremos cómo la forma normal de una función lógica se construye a partir del implicante.
Definición 10. Si para algún estado el implicante está en la posición desactivada (el valor del implante AND (OR) es 1 (0)), decimos que el implicante cubre este estado.
Considere una cierta señal x, para la cual necesitamos calcular una función lógica. Para construir un DNF (CNF), es necesario que los implicantes AND (OR) cubran todos los estados en los que la función x es 1 (0). En este caso, es necesario que ninguno de estos implicantes AND (OR) cubra estados en los que la función x es 0 (1). Además, al calcular las funciones lógicas, es necesario tener en cuenta los detalles de los circuitos: los implicantes deben "superponerse". Es decir, si en algún estado el implicante puede activarse (es decir, se puede activar un evento que es el límite correcto de este implicante) y el valor de la función de señal x no cambia durante esta conmutación, entonces debe haber otro implicante que cubra este estado y no se enciende cuando se activa este evento.
Ahora necesitamos aclarar tres preguntas. ¿Qué es un estado en términos de un gráfico? ¿Cómo determinar los estados en los que la función de señal x es 1 (0)? ¿Cómo determinar las condiciones que cubre el implante?
Comencemos con los estados. Cualquier etiquetado alcanzable es una condición. Como no hay conflictos CSC, cada etiqueta alcanzable corresponde a un estado único (alcanzable). En estados inalcanzables, el valor de la función es arbitrario y no hay necesidad de considerarlos. Por lo tanto, cada estado que consideramos se describe de manera única mediante el etiquetado correspondiente. La posición de cada marcador está determinada únicamente por el arco que marca. Cada arco está asociado de forma única con un par de eventos (ordenados): el evento del que sale el arco y el evento en el que entra el arco. Por lo tanto, cualquier estado alcanzable se describe de manera única mediante un conjunto que consiste en pares ordenados de eventos.
Definición 11. Se escribirán un par de eventos que denotan un arco marcado {P, S}, donde P es el evento de causa y S es el evento de consecuencia.
Definición 12. MM se llamará el conjunto de pares ordenados {P, S}, que describe algún estado alcanzable.
Ahora determinemos para qué estados el valor de la función x es 1, y para qué es 0. Deje que los eventos x + sean causados por n eventos A1, A2, ..., An y los eventos x- causados por m eventos B1, B2, ..., Bm.
El valor de la función x es 1 si:
o 1) para cada i de 1 a n, el par {Ai, x +} pertenece al conjunto MM;
o 2) un par {x +, S} tal que x +> S> x- pertenece al conjunto MM;
o 3) un par {P, S} tal que x +> P> x- yx +> S> x- pertenece al conjunto MM;
o 4) un par {P, x-} de modo que x +> P> x- pertenece al conjunto MM y existe i de 1 a m de modo que el par {Bi, x-} no pertenece al conjunto MM.
El valor de la función x es 0 si:
o 1) para cada i de 1 a m, el par {Bi, x-} pertenece al conjunto MM;
o 2) un par {x-, S} tal que x-> S> x + pertenece al conjunto MM;
o 3) un par {P, S} tal que x-> P> x + yx-> S> x + pertenece al conjunto MM;
o 4) un par {P, x +} tal que x-> P> x + pertenece al conjunto MM y existe i de 1 a n tal que el par {Ai, x +} no pertenece al conjunto MM.
Ahora descubrimos qué condiciones cubre el implante. Deje que el implicante tenga n límites izquierdos L1, L2, ..., Ln ym límites derechos R1, R2, ..., Rm.
El implicante no cubre el estado descrito por el conjunto MM si al menos uno de los pares {P, S} que pertenecen al conjunto MM cumple la siguiente condición: existen i de 1 a n y j de 1 a m de modo que
1) Li y S son el mismo evento y Rj> P> Li,
o 2) Rj y P son el mismo evento y Rj> S> Li,
o 3) Rj> P> Li y Rj> S> Li.
Esta afirmación es verdadera en virtud de la quinta propiedad de las variables.
El implicante cubre el estado descrito por el conjunto MM si para ninguno de los pares {P, S} que pertenecen al conjunto MM se cumple la siguiente condición: existen i de 1 a n y j de 1 a m de modo que
1) Li y S son el mismo evento y Rj> P> Li,
o 2) Rj y P son el mismo evento y Rj> S> Li,
o 3) Rj> P> Li y Rj> S> Li.
Esta afirmación es verdadera en virtud de las propiedades segunda, tercera y cuarta de las variables.
Hablando en sentido figurado, un implicante cubre el estado si todos los marcadores están entre los límites izquierdo y derecho del implicante. Si al menos un marcador se encuentra fuera de estos límites, el implante no cubre este estado.
Ahora tenemos una herramienta para calcular formas normales (todavía no está claro, sin embargo, todavía hay una pregunta con los implantes intermitentes). Pero estamos interesados en formas normales mínimas (teniendo en cuenta los detalles de los circuitos). Antes de continuar, volvamos a la consideración de los implicantes intermitentes. Considere el implicante I para la señal DNF x (el caso con el implicante OR para CNF es similar). Suponga que los dos límites izquierdos de los mismos implicados L1 y L2 no son paralelos entre sí y L1> L2> x- (el caso para dos límites derechos se considera de manera similar). Entonces debe haber dos límites correctos de los implicados R1 y R2 de tal manera que para los pares de L1 y R2, y L2 y R1, se deben satisfacer las propiedades segunda, tercera, cuarta y quinta de las variables. Si hay un límite izquierdo L3 paralelo a L1, entonces para el par L3 y R2 también se deben cumplir las propiedades anteriores (de manera similar, en el caso de la existencia de límites correspondientes, implicantes que son paralelos a los límites L2, R1 y R2). Pero, dado que no se utilizan múltiples señales, debe haber un implicante no discontinuo con límites L1 y R2 (y con límites correspondientes paralelos, si alguno de los implicados interrumpidos los tuviera). Además, el implicante no discontinuo consiste en menos variables y cubre todos los estados cubiertos por el implicante discontinuo, en el que la función de señal x tiene un valor de 1. De ahí la conclusión: los implicantes discontinuos no son extremos y no pueden usarse para calcular funciones mínimas.
Más sobre el cálculo de funciones mínimas en la siguiente parte.