Ciudad sin atascos

CAPITULO DOS
( enlace al primer capítulo )

El arte de diseñar redes viales

Problemas de transporte de la ciudad a través de los ojos de una persona de Computer Science

Si me recomendaran un artículo titulado "El arte de diseñar redes de carreteras", inmediatamente preguntaría cuántas redes de carreteras se construyeron con la participación de su autor. Debo admitir que mi actividad profesional estaba lejos de la construcción de carreteras y recientemente se asoció con el diseño de microprocesadores, donde, entre otras cosas, me dediqué al consumo de recursos para el cambio de datos. Dio la casualidad de que mi mesa estaba justo enfrente de la ventana panorámica, que abría una hermosa vista de la larga sección de la autopista de Volgogrado y parte del Tercer Anillo de Transporte con sus interminables embotellamientos de mañana a tarde, de horizonte a horizonte. Y entonces, un día, de repente me di cuenta: "Maldita sea, porque las complejidades del proceso de cambio de datos con el que lucho en un chip deberían ser exactamente similares a las dificultades que encuentra el flujo de automóviles dentro de la red de calles".
Probablemente, fue solo una vista desde el exterior y la aplicación de métodos que no eran tradicionales para el área estudiada lo que me dio la oportunidad de comprender la causa de los atascos de tráfico y hacer recomendaciones sobre cómo superar su problema en la práctica.

Entonces, ¿cuál es la novedad del enfoque?

Históricamente, se considera que el objetivo principal de las carreteras es la oportunidad que brindan para viajar rápidamente largas distancias (entre Roma y las provincias). Tal juicio se justifica cuando se trata de la red de autopistas interurbanas a nivel federal: las ciudades que conectan parecen pequeños puntos raros en el atlas, y la mayoría de los automóviles que viajan entre estas ciudades pasan por su lado sin girar a ninguna parte.

Sin embargo, solo es necesario pasar varias páginas y abrir un mapa detallado de alguna gran ciudad, ya que la imagen cambia de inmediato: las direcciones solas, donde se puede iniciar o completar el viaje, ya son alrededor de diez mil, todas ellas son bastante densas y relativamente De tamaño pequeño. Al mismo tiempo, cientos de miles de automóviles pueden estar en movimiento en las calles de dicha ciudad a la vez, además, el objetivo de cada uno de ellos no es solo llenar carreteras ya vacías, sino mover a una persona o carga de un punto con una dirección específica " X " a un punto con una dirección específica " Y ". En conjunto, esto significa que el sistema de transporte urbano debe adaptarse para resolver eficazmente el problema del direccionamiento paralelo múltiple . Por lo tanto, las funciones del sistema de transporte urbano se vuelven aún más similares a la red telefónica o informática que la red vial interurbana.

Considerar la red de carreteras como un circuito de conmutación para un desarrollador o ingeniero de hardware en el campo de las tecnologías de transferencia de información es una forma completamente natural de hablar sobre un problema, pero entre las personas involucradas en la investigación sobre problemas de transporte, esta visión es, hasta donde yo sé, nueva.

La teoría de la conmutación de señales es una ciencia de ingeniería limitada, y por sí sola, por supuesto, no será suficiente para planificar una calle, cruce de carreteras o predecir el comportamiento de un flujo de tráfico en una sección recta y aislada de una carretera. Afortunadamente, los problemas enumerados anteriormente están bien investigados hoy en día, y los métodos desarrollados para resolverlos ya se han utilizado con éxito. La teoría de la conmutación, a su vez, permite al arquitecto deshacerse del riesgo cuando todos los elementos de la red de carreteras se ejecutan perfectamente, y la ciudad aún se encuentra en un estado de colapso del transporte. Este riesgo existe porque realizar múltiples direcciones concurrentes requiere muchos recursos.
tarea que requiere mucho tiempo, la clave para una solución efectiva no es tanto el ancho de las calles y la conveniencia de los intercambios de transporte, sino la elección competente de qué esquema de conmutación particular implementará la red de carreteras propuesta.

A partir de este trabajo, por ejemplo, descubrirá por qué las redes de transporte de tipo "arterial", que todavía se utilizan a menudo en las ciudades modernas, son "malas" y con el crecimiento de la población necesariamente conducirán a embotellamientos. Otro resultado interesante, que está bien de acuerdo con las observaciones, explica por qué la expansión de las carreteras por sí sola, si antes de que ocurrieran todos los atascos de tráfico exclusivamente en las proximidades de los intercambios, es poco probable que mejore la situación, incluso si el número de automóviles en la ciudad sigue siendo el mismo.

Cuando escribí este artículo, era importante para mí que fuera comprensible para el arquitecto más común, que pudiera ser útil a través de su trabajo. Traté de introducir al lector en temas de cambio en un lenguaje simple, para desarrollar criterios para evaluar qué tan bien una red de carreteras en particular hará frente a la tarea de direccionamiento paralelo, usando ejemplos modelo que mostré cómo usar este conocimiento en la práctica.

El artículo está dirigido a un amplio círculo de lectores que están un poco familiarizados con el curso universitario de matemáticas, la teoría de algoritmos y están listos para dedicarle de 1 a 5 días.

Separación y fusión de flujos de automóviles.

Obvio para muchos conductores, la observación es que las dificultades de tráfico surgen principalmente en aquellos lugares de la carretera donde los automóviles, por alguna razón, se ven obligados a cambiar de carril. Los ejemplos incluyen bifurcaciones, estrechamientos, áreas de unión y caminos de acceso a autopistas, secciones de una autopista donde algunos carriles están bloqueados por un accidente o reparación de caminos.
En esta sección, se intentará dar una descripción cuantitativa de los procesos que ocurren en tales casos, y comenzaremos por comprender cómo se reconstruyen los automóviles de un carril a otro.

Dos estrategias para reconstruir en una fila adyacente

El movimiento del tráfico a lo largo de la carretera tiene un desnivel natural: alguien prefiere conducir un poco más rápido, alguien un poco más lento, la distancia entre un automóvil disminuye y se vuelve difícil de manejar, mientras que entre los demás aumenta tanto que permite que los automóviles se ajusten. de carriles adyacentes. La aparición de tales brechas en el flujo del carril adyacente directamente en el lado del conductor aleatorio puede ser frecuente o poco frecuente. Si, en el momento en que necesita hacer una maniobra, no hay espacio, el conductor puede recurrir a al menos dos estrategias de comportamiento:

Estrategia no 1
Varios espacios adecuados pueden simplemente ubicarse cerca de su ubicación. Si el movimiento es lo suficientemente denso, entonces es poco probable que el conductor pueda agregar velocidad y atrapar el espacio necesario, pero desacelere un poco el movimiento y permita que la corriente vecina se adelante para igualar el espacio que originalmente estaba detrás, no habrá grandes problemas. Los costos de esta estrategia son obvios: el propio conductor y los automóviles que circulan por su carril pierden algo de tiempo debido a la necesidad de reducir la velocidad.

Estrategia no 2
Para esperar, debes tener paciencia y tener el tiempo necesario para esto. Una alternativa puede ser un intento de realizar la maniobra necesaria "aquí" y "ahora". Según esta idea, el conductor da una señal a los autos detrás de él de la franja en la que se va a mover. Aquellos, a su vez, en respuesta a su señal deberían reducir la velocidad un poco y "soltar" hacia adelante, los autos que se mueven frente a ellos, dando así al espacio el tamaño necesario, se formarán en su flujo. Los costos de tiempo en este caso se distribuyen entre los autos del carril donde el conductor finalmente reconstruyó.

En la vida real, ambas estrategias están involucradas al mismo tiempo: primero, el conductor reduce la velocidad, esperando una brecha relativamente grande en la corriente del carril vecino, y solo luego da una señal a los autos que se mueven en él sobre su intención de realizar una maniobra de reconstrucción.

Por supuesto, las entradas, las rampas y los estrechos no son la única razón del cambio de carril a carril, que vale la pena recordar al diseñar carreteras. La capacidad de los automóviles con velocidades más altas para adelantar el tráfico sin prisas es necesaria para que la situación en la carretera no se degrade a una gran cola que se arrastra a la velocidad del tractor más lento. Sin embargo, el problema de la coexistencia de vehículos que se mueven a diferentes velocidades en la carretera tiene una naturaleza ligeramente diferente y puede separarse de los problemas considerados en este artículo, ya que el proceso de adelantamiento y las reorganizaciones asociadas no son para el conductor acciones forzadas que requieren que se apresure . Si hay tiempo para esperar, entonces, según la teoría de la probabilidad, es una oportunidad conveniente para realizar una maniobra para dejarla solo al conductor y para esto no interfiere necesariamente con el movimiento de otros automovilistas.

Costo de un movimiento.
El comportamiento de los conductores en realidad puede ser muy difícil, pero es importante para nosotros, en primer lugar, que el resultado obtenido bajo las condiciones del modelo siga siendo plausible: cada movimiento forzado de un automóvil de un carril a otro impone una penalización temporal a los participantes del tráfico.

Vamos a evaluar ahora cómo la cantidad de tiempo perdido depende de la densidad de los automóviles en la carretera.

Consideraremos el movimiento a lo largo de cada carril como una corriente separada. Al tratar de mantenerse a una distancia cómoda de los automóviles que se encuentran en el mismo carril, los conductores reservan una parte de cierta longitud característica d en la corriente. Deje que los autos ρ caigan en una corriente por unidad de longitud. Acordamos llamar pequeña a la densidad de flujo o, lo mismo, decir que ρ es pequeño si el producto ρ × d es mucho menor que la unidad.

En el momento en que el conductor se da cuenta de la necesidad de pasar a la siguiente fila, la probabilidad de que la sección de la cantidad d que iba a ocupar allí no sea libre, a una pequeña ρ será aproximadamente proporcional a la misma. Si el evento descrito realmente se lleva a cabo, entonces en total dos autos que compiten por un lugar experimentarán como resultado de las maniobras algún retraso en el valor constante promedio δ .

Suponiendo que ρ es pequeño, puede despreciarse la probabilidad de que sus acciones en este momento afecten el movimiento de otros automóviles. Por lo tanto, en el primer orden de pequeñez con respecto a ρ , la pérdida de tiempo de un movimiento será α ⋅ ρ , donde el coeficiente α es una cantidad medible empíricamente, dependiendo de la cultura, el clima, los límites de velocidad (y así sucesivamente), pero permaneciendo aproximadamente constante localmente en el tiempo y durante Esta ciudad en su conjunto.

La intensidad de las pérdidas en el sitio antes de la salida.
Los autos que salen para el congreso, antes de llegar a la rampa (Fig. 2), deben, a veces incluso varias veces, ser reconstruidos en la fila adyacente a la derecha. Cada una de estas maniobras dificulta el movimiento y, como resultado, la velocidad promedio en la sección antes de la salida es notablemente más baja que en las secciones de "tránsito" (privado de las salidas, "entradas" y bifurcaciones) de la autopista.


fig. 2

Para pasar una parte del camino a una velocidad más baja, los conductores (y sus pasajeros) se dan la vuelta a la cantidad de tiempo adicional que pasan en el viaje. En otras palabras, el área de la carretera directamente adyacente a la rampa es un generador constante de pérdidas temporales.

Suponga que la velocidad media de la máquina ν y la densidad de flujo ρ en el límite frontal de esta región son las mismas para todas las bandas.

Supongamos, además, que la densidad ρ y la velocidad de flujo q que salen de la salida (el número promedio de autos que ingresan a la rampa por unidad de tiempo) son simultáneamente pequeños, y s es el número de carriles en la carretera. Para llegar a la salida, el conductor realizará 1 a s maniobras de reconstrucción. Si la densidad de flujo en la rampa es mucho menor que ρ , solo la última maniobra le costará prácticamente “gratis”, mientras que el resto en cualquier caso causará pérdidas de α ⋅ ρ . En promedio, tendrá que realizar (0 + 1 + 2 + ... + s - 1) / s = ( s - 1) / 2 maniobras "caras".

Dadas las dificultades causadas por todos los autos que se van al congreso, podemos escribir la fórmula para la intensidad de las pérdidas temporales:

I _out = q ⋅ α ρ ⋅ ( s - 1) / 2 = ( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 - 1 / s )

El valor p = ( sρν ) no es más que la velocidad de flujo de todos los automóviles que se mueven a lo largo de la carretera en la dirección en cuestión (el número promedio de automóviles que pasan por la columna por unidad de tiempo). El último comentario nos da la oportunidad de reescribir la fórmula para I en una forma más simétrica:

I _out = ( α / 2 ν ) ⋅ pq ⋅ (1 - 1 / s )

Tasa de pérdida en la sección contigua de la carretera de acceso
La situación que surge en la carretera detrás del lugar donde el camino de acceso se conecta con ella repite en gran medida la situación en el sitio frente al congreso, aunque hay algunas diferencias.
Deje que una pequeña corriente de automóviles de potencia q a través de la rampa lateral vierta el tráfico principal de la autopista (Fig. 3).


fig. 3

La rampa tiene solo una longitud finita, por lo que todos los autos recién llegados deben incorporarse en el carril de la derecha de la autopista. Como resultado, la densidad del tráfico en el carril más a la derecha es localmente más alta que el promedio en la carretera, por lo que algunos de los conductores deciden cambiar de carril a una fila adyacente menos concurrida a la izquierda, lo que, a su vez, conduce a un aumento local de la densidad en el segundo tira. Este proceso de migración entre bandas continuará hasta que la densidad del flujo se nivele en todo el ancho de la autopista. Suponiendo que la velocidad media ν sea la misma para todas las n bandas, podemos esperar que, una vez finalizados los procesos de migración, la potencia de flujo en cada una de ellas aumente exactamente (1 / s ) ⋅ q .

Para ver cuánto cuesta ese "enroque" a los conductores, primero calculamos la potencia de todos los flujos de migración. El flujo desde la rampa hasta el primer carril de la autopista ya lo conocemos: es igual a q . Para obtener un equilibrio en forma de un aumento de (1 / s ) ⋅ q , el flujo hacia el segundo carril desde el lado del primero ya debe ser (1 - 1 / s ) ⋅ q , desde el segundo hasta el tercero - (1 - 2 / s ) ⋅ q , desde el lado k hasta el ( k + 1) th - (1 - k / s ) ⋅ q . De acuerdo con la última fórmula, la capacidad del flujo de migración hacia el carril más a la izquierda será (1 - ( s - 1) / s ) ⋅ q = (1 / s ) ⋅ q , según lo ordena el sentido común.

Como conocemos el tiempo de penalización de una sola reconstrucción y el poder de todos los flujos de migración, ahora podemos calcular la intensidad total de las pérdidas generadas por ellos:

I _in = α ρ ⋅ q + α ρ ⋅ (1 - 1 / s ) ⋅ q + α ρ ⋅ (1 - 2 / s ) ⋅ q + ... + α ρ ⋅ (1 / s ) ⋅ q =

α ρ q (1 + 2 + ... + s ) / s =

α ρ q ( s + 1) / 2 =

( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 + 1 / s ).

Recordando nuevamente que sρν es la potencia p del flujo de todos los automóviles a lo largo de la carretera, obtenemos la fórmula del costo en su forma final:

I _in = ( α / 2 ν ) ⋅ pq ⋅ (1 + 1 / s ).

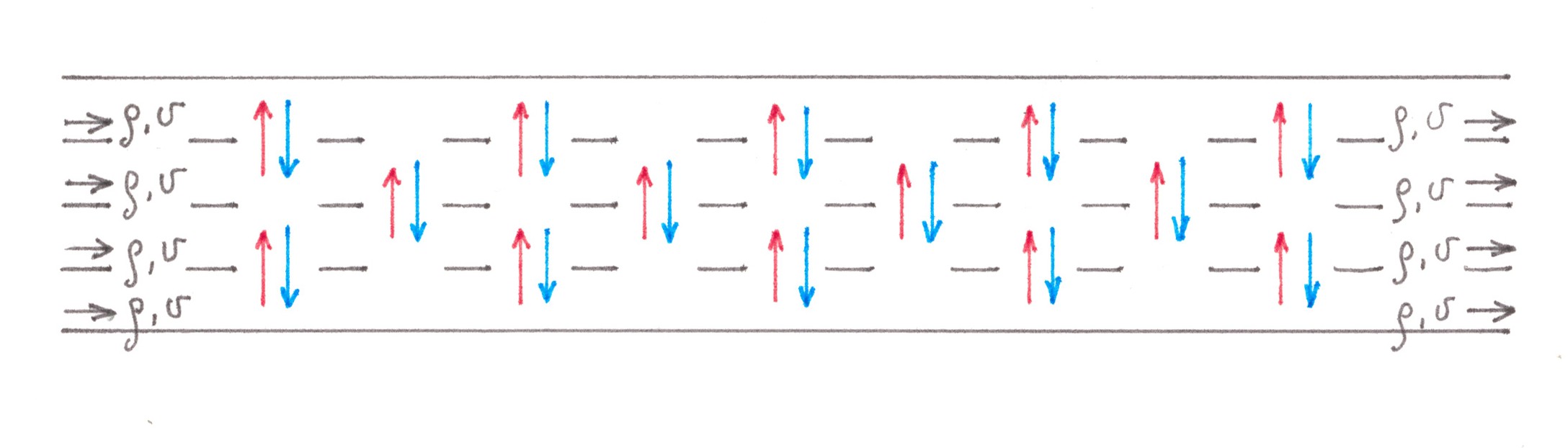
Tasa simétrica de pérdida de horquilla
En los párrafos anteriores, encontramos pérdidas por la interacción de flujos, uno de los cuales era necesariamente grande y el otro era necesariamente pequeño. Para demostrar el enfoque para resolver problemas cuando las capacidades de ambos flujos son comparables en magnitud, consideremos otro extremo: una bifurcación en la que ambas direcciones "secundarias" son igualmente populares para los conductores (Fig. 4).


fig. 4 4

Por conveniencia, los autos que van a la derecha en la bifurcación se llamarán "azules" y los autos que salen a la izquierda - "rojos". Inicialmente, los automóviles de ambos "colores" se mueven mezclados, dispersos entre los 2 carriles de la carretera. A medida que se acercan al cruce, los autos rojos comienzan a desplazarse lentamente hacia los n carriles izquierdos, y los azules hacia el derecho s , carriles: la migración fluye en ambas direcciones entre carriles adyacentes. A diferencia del ejemplo del camino de acceso, estos flujos ya no son "relativamente pequeños". Por cierto, solo entre los dos carriles centrales hay un intercambio de tráfico forzado, cuya intensidad en cualquiera de las direcciones (de izquierda a derecha o de derecha a izquierda) es igual a una cuarta parte de la potencia de toda la corriente que se mueve a lo largo de la carretera de los automóviles. Afortunadamente, en esta situación hay una manera suficientemente buena de estimar los costos generados. Primero, notamos que el proceso de dividir los autos en "rojo" y "azul" probablemente comienza mucho antes de la bifurcación y continúa lentamente, por lo tanto, por un lado, debería tener poco efecto sobre la densidad del tráfico en una fila separada, y por otro, hacer la migración los flujos se extendieron a lo largo de largas distancias, lo que brinda la oportunidad de representar cada uno de ellos como una combinación de una gran cantidad de flujos de baja potencia (Fig. 5).


fig. 5 5

Como ahora estamos hablando de pequeños flujos, aunque en grandes cantidades, nada nos impide reducir el problema en consideración a los ya resueltos. Divida mentalmente la carretera en el centro en dos partes iguales y luego conéctelas con una gran cantidad de caminos de un solo carril, permitiendo que los autos rojos lleguen al lado izquierdo y los azules a la derecha (Fig. 6). Debido a la simetría obvia, al calcular las pérdidas generadas, podemos enfocarnos en máquinas de cualquier color, por ejemplo, azul, y al final simplemente duplicar el resultado.


fig. 6 6

Por lo tanto, deje que la velocidad ν y la densidad ρ sean las mismas para todos los carriles y permanezca constante en toda el área donde los automóviles están separados por colores.En este caso, la velocidad de flujo de todos los automóviles que se mueven a lo largo de la carretera será:

p = 2 sρv .

Supongamos que q ₁ , q ₂ , ... q _m denotan los flujos de automóviles azules que se mueven a lo largo de puentes imaginarios hacia la mitad derecha de la autopista. Supongamos que poco antes del sitio de separación en cada carril de la autopista, ambos colores se representan con proporciones iguales del 50%, lo que implica que en el total
q ₁ + q ₂ + ... + q _m son iguales a sρv / 2, que es p / 4.

Pérdidas generadas por la secuencia q_i , debido a su pequeño tamaño, podemos calcular mediante la fórmula:

I _i =I _out +I _in = (α/ 2ν)⋅(p/ 2)⋅ q _i (1 - 1 /s) + (α/ 2ν)⋅(p/ 2)⋅ q _i (1 + 1 /s) = (α/ 2ν)p q _i

Sumando la última expresión sobre todoi, Encontrar la pérdida generado coches sólo azules:

I _azul = ( α / 2 ν ) ⋅ p ⋅ ( q ₁ + q ₂ + ... + q _m ) = ( α / 2 ν ) p ² /4.

La pérdida completa, como ya se mencionó, se duplicará y la cantidad doble de:

I _div = ( α / 2 ν ) p ² /2.

Análisis de las fórmulas obtenidas
Si separamos la intensidad Ies decir, la cantidad de tiempo total de participantes perdidos por segundo por la cantidad de flujo lateral q , que por definición es igual a la cantidad de automóviles que se conectan o dejan el tráfico en la autopista en un segundo, obtenemos las pérdidas promedio generadas por uno de estos automóviles:

i _in = I _in / q = ( α / 2 ν ) ⋅ p ⋅ (1 + 1 / s )

i _out = I _out / q = ( α / 2 ν ) ⋅ p ⋅ (1 - 1 /s )

Quizás lo más importante en estas fórmulas es la proporcionalidad directa entre el flujo de energía de los automóviles en la autopista py los costos unitarios i . Todo parece como si un automóvil buscara unirse, o viceversa, para dejar el flujo del movimiento principal, causando daños constantes a todos los conductores cercanos.

La segunda observación, interesante y muy inesperada, se refiere al efecto extremadamente débil sobre la intensidad de las pérdidas generadas del número de carriles cerca de la carretera directamente al lado del cruce. Como puede ver, mirando la fórmula de I _out , el congreso es generalmente el más barato para una carretera de un solo carril ( s = 1, i _out = 0), y las dificultades causadas por la carretera de acceso contigua para una carretera de tres carriles y una de seis carriles difieren solo en un

100% ⋅ [(1 + 1/3) - (1 + 1/6)] / (1 + 1/3) = 12,5%.

Si tenemos en cuenta que todos los automóviles que alguna vez se han unido al tráfico en la autopista eventualmente tendrán que abandonarlo, entonces parece bastante legalusar el valor unificado i _av = ( i _in + i _{in en} lugar de i _in and i _out ) / 2 = ( α / 2 ν ) ⋅ p .



A pesar de la ausencia en la fórmula para i _{av de} una dependencia explícita en el número de carriles, debe recordarse que su conclusión (ver las suposiciones para I _in y I _out ) se basa en gran medida en el supuesto de baja densidad de automóviles en la carretera, por lo que es poco probable que dé resultados satisfactorios, siendo aplicado a una carretera demasiado estrecha con demasiado tráfico.

Hallazgos preliminares
En áreas cercanas a los cruces, el tráfico ocurre inevitablemente, quitando tiempo a los conductores, reduciendo la velocidad promedio, esto último conduce a un aumento en la densidad de los automóviles y, como consecuencia, a la posible ocurrencia de atascos. Los costos de tiempo asociados con la separación y fusión de los flujos de automóviles se denominarán conmutación.

Las pérdidas de un tipo similar están presentes de una forma u otra en cualquier esquema de conmutación: ya sea una red telefónica o informática, un microprocesador de múltiples núcleos o un servicio de entrega de correo.

Cuando un conductor se une o, por el contrario, deja el tráfico en la carretera, los costos de cambio incurridos por sus acciones son proporcionales a la potencia del flujo de automóviles observado en ese momento en la carretera.

Para reducir las pérdidas de conmutación en toda la ciudad, es necesario considerar cuidadosamente la red de carreteras implementada en ella en la etapa de diseño. Un poco más tarde analizaremos esta tarea en detalle, pero ahora se pueden enumerar algunas recomendaciones obvias:

1. las pérdidas de conmutación son proporcionales a la capacidad de flujo en la carretera: no es necesario ampliar las carreteras sin la necesidad, dos autopistas pequeñas son el doble de buenas que una grande;
2. las pérdidas de conmutación son proporcionales a la potencia de los flujos laterales: vale la pena diseñar la red para que el conductor tenga que desviarse lo menos posible durante su viaje;
3. la interferencia mutua causada por los conductores de las corrientes principales y secundarias debería reducirse a escala de toda la ciudad si intenta evitar rutas que se superponen solo en una sección corta de la pista en una secuencia.

Prerrequisitos económicos para la existencia de ciudades.
Modelo de ciudad de acceso uniforme

Quizás lo primero para comenzar cualquier proyecto de planificación (o re-planificación) del sistema de transporte de la ciudad es tratar de determinar qué tipo de migración realmente necesita la ciudad ahora y cómo cambiarán sus necesidades en el futuro.

Tal análisis puede llevarse a cabo si primero divide la ciudad en zonas territoriales no demasiado grandes, pero no demasiado pequeñas, y luego, para cada par de dichas zonas, indique qué número aproximado de viajes a un lado o al otro necesitan sus habitantes en uno u otro momento del día Al colocar las predicciones hechas en una tabla cuadrada, recibirá una matriz de las necesidades de migración de los residentes de la ciudad.

Es por esta matriz que vale la pena buscar una red que permita a los conductores y pasajeros pasar el menor tiempo posible en un viaje separado y requiera a las autoridades de la ciudad la menor cantidad de recursos posible para su construcción.

Cuando se trata de ciudades existentes, es importante no cometer un error y no reemplazar el número de viajes que la gente realmente necesita con el número de viajes que históricamente se han establecido bajo la influencia de algunos obstáculos o dificultades en el momento del trabajo de diseño. Probablemente, la red de transporte de Berlín "antes" y "después" de la caída del muro de separación puede servir como la ilustración más llamativa de lo que se ha dicho.

Esta sección se ocupará principalmente de cuestiones humanitarias en las que no soy especialista, pero creo que discutirlas como aficionado es, sin embargo, más correcto que simplemente evitar el problema.

Para representar mejor las necesidades migratorias de la población, vale la pena comenzar con la pregunta fundamental: "¿Por qué las ciudades realmente necesitan y qué función útil desempeñan?" .

Intentemos responderlo no como residentes ordinarios de ciudades (y pueblos), sino desde la perspectiva de la persona responsable del proceso de urbanización en algún estado grande y desarrollado. Desde este punto de vista, ya no es importante los motivos históricos que alguna vez hicieron que tanta gente se apiñara en un pequeño pedazo de tierra, o las razones por las que continúan haciéndolo ahora, es importante: qué efecto económico crea ciudades de un tamaño u otro y para debido a qué mecanismos se logra este efecto.

En mi opinión, la razón principal de la existencia de grandes ciudades es, por un lado, la oportunidad para que las empresas de tecnología encuentren empleados de profesiones raras y, por otro lado, la oportunidad para que las personas que dominan profesiones raras vendan sus servicios a empresas interesadas en ellos en términos competitivos. En una ciudad pequeña (no especializada), la producción de muchos bienes y servicios es simplemente imposible, o pone a las empresas de tecnología y a sus empleados que la implementan en la posición de rehenes mutuos, sin dar a uno u otro ninguna alternativa.

Por ejemplo, tome la profesión no tan rara de un maestro de literatura escolar. Según las estadísticas, la necesidad de ellos es: aproximadamente 1 maestro por cada 1000 habitantes. En una escuela regular, 3-4 personas enseñan literatura. La elección de un trabajo para un profesor de literatura se puede llamar competitiva si hay al menos 4-5 escuelas secundarias en su ciudad, que, en términos de población, es de aproximadamente 15 mil personas.

Aparentemente, las personas con una especialidad de ingeniería se sienten cómodas en el mercado laboral en ciudades con una población de al menos 100 mil. Por supuesto, también existen tales profesiones, cuya demanda solo aparece en ciudades con un millón de personas, pero el sentido económico de las ciudades multimillonarias sigue siendo un misterio para mí.

Después de todo lo anterior, dos hipótesis parecen bastante motivadas (la validez de las cuales, sin embargo, no afecta la verdad del contenido principal del artículo):

1. los viajes más frecuentes que un adulto promedio necesita recorrer distancias que capturan 4-5 de los trabajos más prometedores para él;
2. Para una parte importante de la población que posee las profesiones raras y económicamente más valiosas, la distancia de los viajes más frecuentes puede ser comparable con el radio de la ciudad.

Como un reflejo mejorado de las hipótesis 1) y 2), en mis ejemplos a menudo usaré el modelo de la ciudad con "acceso uniforme", suponiendo que el poder de los flujos de viaje exigidos sea el mismo entre dos cuartos o, en otras palabras, en todas las celdas de la matriz la migración necesita el mismo número positivo. Si observa aleatoriamente los registros de los viajes realizados en esa ciudad durante el día, entonces, para el próximo viaje marcado, todos los trimestres tendrán las mismas posibilidades de ser el comienzo de este viaje y servirlo como el final, y no hay relación entre la posición de la "inicial" y la "final" »No se deben observar cuartos.

Redes de topología de red simple

Intentemos aplicar las ideas descritas en los párrafos anteriores a algunos tipos de planes de la ciudad tomados de la vida.

Ciudad lineal
Los primeros asentamientos grandes se originaron predominantemente a lo largo de la costa, en áreas de una delgada franja de tierra entre el mar y los acantilados, o a lo largo de los caminos de carreteras transitadas, por lo que en el proceso de crecimiento adquirieron estrechas fronteras alargadas. Muchos de estos asentamientos han sobrevivido hasta nuestros días, conservando su forma alargada y convirtiéndose en ciudades modernas (ilustración a continuación).


(área aislada de Río de Janeiro, autor desconocido)

A menudo, en una ciudad así, solo hay un camino ancho alrededor del cual se construye. Suponga que cada barrio (zona de división territorial) genera una corriente de viajes de una sola capacidad, de todos esos barrios - n , y la ciudad misma obedece al modelo de migración de "acceso uniforme".


fig. 7 7

Intentemos encontrar para las condiciones enumeradas anteriormente cómo el tiempo de viaje promedio y el área de carretera requerida cambian con el aumento de n .

Entonces, deje que todos los cuartos tengan la misma forma y tamaño, y su número aumenta en λ (lambda) veces. Obviamente

• La longitud de la carretera principal aumenta en un factor de λ .

En virtud del modelo adoptado de "acceso uniforme", el 50% de los viajes que comenzaron en la mitad derecha de la ciudad terminan en su mitad izquierda (exactamente lo contrario), por lo tanto, con un aumento en el número de barrios por un factor de λ, la potencia de la corriente que pasa por el centro de la ciudad también aumentará en λ veces Un razonamiento similar con la misma conclusión será cierto si, en lugar del medio, tomamos algún punto dividiendo la ciudad en una proporción dada (1: 3, 2: 5), lo que implica que

• El flujo de potencia de los automóviles a lo largo de la carretera principal aumenta en un factor de λ .
• El número de carriles de la carretera principal requerido en cada sección aumenta λ veces.

Más o menos obvio que la duración promedio del viaje, y con ella

• El tiempo de viaje neto dedicado a cubrir la distancia aumenta en un factor de λ .

Todo lo que nos queda es calcular cuántas veces aumentará el tiempo perdido debido a los costos de cambio en un viaje. En cada trimestre, una corriente lateral de energía de la unidad entra y sale, lo que en conjunto genera pérdidas temporales de intensidad:

I = I _in + I _out = ( α / 2 ν ) p ⋅ 2,

donde p es el caudal en la carretera principal. Ya sabemos que el número de trimestres y la velocidad de flujo en la carretera principal aumentan como λ , por lo tanto, las pérdidas de tiempo totales generadas por la red aumentan en un factor de ² . Por otro lado, el número de viajes generados por la red, entre los cuales como resultado se distribuyen todas estas pérdidas, aumenta en un factor de λ , de donde obtenemos que

• El tiempo de viaje neto perdido debido a los costos de cambio aumenta en un factor de λ .

Recolectemos todos los resultados en una placa:

Topología lineal
El número de puntos de dirección (trimestres) de capacidad de la unidad ............................... n
El área total de carreteras ............................................... ........................................ O ( n ² )
Tiempo de viaje puro
gastado en cubrir la distancia .............................................. ..... O ( n )
Tiempo de viaje puro
perdido debido a los costos de cambio ............................................ ......... O ( n )
El número de nodos de conmutación ............................................... .................................... O ( n )
El número de nodos de conmutación, teniendo en cuenta la potencia de los flujos laterales ..................... O ( n )

Notación utilizada: " y = O ( x )", significa que las cantidades x e y son funcionalmente dependientes, y cuando x crece sin límites, la relación x / y tiende a un número finito distinto de cero.

Ciudad celular
El segundo método de planificación bastante común es organizar los bloques en forma de una matriz rectangular, similar a cómo se colocan las piezas en porciones en una barra de chocolate.

Acordamos llamar a estas ciudades "Celular".


(Los Ángeles, foto: Stepanov Glory)

La Figura 8 muestra un diagrama de la Ciudad Celular, compuesta de n (teniendo en cuenta las "mitades") de los cuartos, formando juntos un cuadrado regular. Los cuartos están separados entre sí por un total de √ n caminos, que se ejecutan condicionalmente de oeste a este, y otros √ n caminos, que se extienden de sur a norte. En total, estas carreteras forman √ n × √ n intersecciones, cada una de las cuales puede hacerse como una intersección de semáforo o implementarse a través de un puente de carretera y pasos elevados.


fig. 8

Independientemente de si el tráfico en las calles es unidireccional o bidireccional, cualquier viaje desde el punto "A" hasta el punto "B" en una ciudad a cuadros puede realizarse a lo largo de una ruta que atraviesa no más de dos calles y no requiere más de un giro en la intersección querido

Supongamos que, como en el ejemplo anterior, cada trimestre genera una corriente de viajes de capacidad unitaria, y las necesidades de migración de la población se describen mediante el modelo de "acceso uniforme". Calculemos, ahora para la Ciudad Celular, aquellas leyes por las cuales el tiempo promedio de viaje y el consumo de recursos de construir una red de carreteras con un aumento en el número de trimestres cambian.

Si el número de trimestres aumenta en un factor de λ , entonces:

• el área de la ciudad aumenta en λ veces, y sus dimensiones lineales mientras mantiene las proporciones -
  en √ λ ,
• la longitud de viaje promedio y el tiempo neto para cubrir la distancia, siendo proporcional a las dimensiones lineales, aumentan √ λ veces,
• la cantidad de calles y la cantidad de vecindarios adyacentes a una calle aumenta √ λ veces,
• La potencia del flujo de tráfico, que es proporcional al número de trimestres con los que el flujo está "en contacto" (más adelante se dará una explicación de este hecho), aumenta en √ λ veces,
• el área requerida de todas las carreteras crece a medida que (número de calles) × (longitud de una calle) × (potencia del flujo de la calle) = √ λ ⋅ √ λ ⋅ √ λ = λ √ λ

Los flujos laterales se dividen en aquellos que van desde o hacia los cuartos y los flujos de tráfico que giran de una calle a otra en sus intersecciones. El primero, según las condiciones, siempre permanece igual a la unidad, después del segundo, si tenemos en cuenta que hay muchos más barrios en la ciudad que barrios en una sola calle, casi todo el tráfico que se mueve a lo largo de ella llega o sale de la carretera de la calle. Como resultado, el cambio en la magnitud de los flujos laterales del segundo puede estimarse mediante la fórmula (cambio en la potencia del flujo de la calle) / (aumento en el número de intersecciones en una sola calle) = √ λ / √ λ = 1. La igualdad de la última relación con la constante sugiere que estos flujos no cambian especialmente con un aumento en el número de trimestres, por lo tanto, el aumento en los costos de conmutación generados por la red en su conjunto será: (aumento en el número total de trimestres + intersecciones) × (cambio en el valor del flujo en una sola calle) = λ √ λ . Como el poder del flujo de viaje generado por todos los trimestres aumentó en λ , entonces

• el tiempo de viaje neto perdido debido a los costos de cambio aumenta en √ λ

Imagine el resultado en forma de tableta:

"Topología celular"
El número de puntos de dirección (trimestres) de capacidad de la unidad ............................... n
El área total de carreteras ............................................... .................................... O ( n √ n )
Tiempo de viaje puro
gastado en cubrir la distancia .............................................. ... O (√ n )
Tiempo de viaje puro
perdido debido a los costos de cambio ............................................ ....... O (√ n )
El número de nodos de conmutación ............................................... .................................... O ( n )
El número de nodos de conmutación, teniendo en cuenta la potencia de los flujos laterales ..................... O ( n )

Al comparar las redes lineales y celulares entre sí, es difícil no darse cuenta de que el aumento de los recursos necesarios para la construcción y el tiempo dedicado a un viaje con el crecimiento de la ciudad para la primera red es mucho más rápido que para el segundo. Por ejemplo, una ciudad celular de 100 barrios requiere 10 veces menos asfalto, y un viaje a través de ella requiere un promedio de 10 veces menos tiempo del necesario en una ciudad lineal del mismo tamaño. Por lo tanto, tiene sentido usar redes de carreteras con topología lineal solo en ciudades muy pequeñas.

Si por un tiempo se olvida de la existencia de costos de cambio, entonces la topología celular puede considerarse una forma ideal de diseñar redes de carreteras, ya que proporciona una estimación O óptima asintóticamente para la longitud promedio del viaje y el área de la carretera requerida. De hecho, para cualquier ubicación más o menos "compacta" de la ciudad (con acceso uniforme), la duración del viaje no crecerá más lentamente que la raíz cuadrada de su área, que generalmente es directamente proporcional a la población. Como resultado, obtenemos todos los mismos O (√ n ).

El hecho de que una ruta típica en Cellular City vaya a lo largo de una "esquina" en lugar de una línea recta, en principio, da derecho a buscar mejores formas de planificar ciudades, pero es improbable un 20% de ahorro (es decir, cuánto puede ganar en el límite si los autos aprenden a atravesar paredes) algún día obligarán a los arquitectos a abandonar la disposición rectangular de calles y carreteras.

El límite más bajo posible del costo de construir (y mantener) la red se puede obtener recordando que cada automóvil reserva parte del carril para su movimiento, como resultado, el área total de las carreteras es proporcional al producto del tiempo promedio de viaje (duración promedio del viaje) por la cantidad de automóviles en la ciudad : O (√ n ) × O ( n ) = O ( n √ n ) (compárese con la tabla de la ciudad de la celda).

Si hablamos de la cantidad de tiempo que se pierde en el viaje debido a los costos de cambio, entonces, sorprendentemente, su relación con la cantidad de tiempo que lleva cubrir la distancia no depende asintóticamente del número de trimestres individuales en la ciudad celular o lineal (O (√ n ) / O (√ n ) = O (1), O ( n ) / O ( n ) = O (1)). En otras palabras, el porcentaje de tiempo perdido en viajes debido al cambio de eventos en la gran ciudad y en la pequeña será el mismo. De esto podemos concluir que, si no hubo problemas serios con los costos de cambio en una ciudad pequeña (por ejemplo, ascendieron a 10-20%), entonces en una gran ciudad aún no deberían observarse, y si lo fueran, entonces ellos mismos no irán a ninguna parte, sin importar cómo creció y se amplió la ciudad.

Dado que no sabemos cuál de las alternativas es verdadera (o más bien, sabemos que existen problemas con el tráfico de automóviles en las grandes ciudades), vale la pena intentar mejorar la topología de Cellular City para que los costos de cambio disminuyan al menos en un tiempo constante.

Ejemplos útiles de redes poco realistas.

Veamos si la topología celular sigue las recomendaciones que hemos desarrollado al analizar la conmutación de flujos en la carretera.

1) No agrande las carreteras sin la necesidad.
- si. El tráfico se distribuye por muchas carreteras (compárese con Linear City).

2) Evite crear condiciones cuando necesite hacer una gran cantidad de vueltas en un viaje.
- si. Es probable que cualquier viaje se realice a lo largo de una ruta que requiera solo un giro en las calles de la ciudad.

3) Evite situaciones al viajar en una sección de la carretera, cuyas rutas tienen solo una pequeña sección de la ruta común.
- Aquí, tal vez, hay algo en lo que trabajar. A pesar del número mínimo de vueltas por viaje, su ruta como parte del flujo de la carretera principal pasa a través de una gran cantidad de nodos de conmutación (O ( n )), en cada uno de los cuales se pierde un tiempo valioso.

El último comentario motiva a investigar la siguiente pregunta: "¿Cuál es el valor mínimo del número promedio de nodos de conmutación a través de los cuales debe pasar un viaje dentro de una red de carreteras que conecta n bloques?"

La tarea de buscar una red de este tipo tiene sentido, por supuesto, solo con la condición de que el número de flujos combinados o compartidos por cualquier nodo de conmutación esté limitado preliminarmente desde arriba por un cierto valor fijo. De lo contrario, siempre puede presentar una red de carreteras con n puntos de dirección y una sola megaunión.


(autor desconocido)

Es mucho más fácil investigar el problema real si antes era posible revelar al menos parte de los patrones utilizando algunos ejemplos de modelos simples, aunque no realistas. Siguiendo esta lógica, nos olvidaremos temporalmente de las limitaciones geométricas de construir un camino para que los viajeros recorran distancias, concentrando toda su atención en cómo las redes abstractas resuelven el problema de direccionamiento paralelo. Con respecto a los nodos de conmutación, asumiremos por ahora que cada uno de ellos divide el flujo en dos partes (el nodo de división) o combina dos flujos en uno.


fig. 9 9

Árbol de direcciones
Deje que haya un punto de dirección inicial donde comiencen todos los viajes sin excepción, y otro n puntos de dirección final en los que finalicen con igual probabilidad (Fig. 9).

Es necesario construir una red de transporte que permita viajar a través de la menor cantidad posible de nodos de conmutación.

La solución obvia (para los programadores), que se plantea aquí, es usar un árbol binario equilibrado, al mismo tiempo que necesita colocar un único punto de partida en la parte superior del árbol, y colocar los n puntos de finalización restantes en cada una de sus hojas (Fig. 10). La red construida de la manera descrita se llamará árbol de dirección directa.


fig. 10

Cambiando las direcciones de todos los flujos al opuesto en el árbol de Dirección directa, obtenemos así el árbol de Dirección inversa, cuyo propósito es conectar n puntos de inicio con un solo acabado.

En los casos en que n es una potencia de dos, cualquier ruta dentro del árbol de Dirección pasa exactamente a través _de los nodos de conmutación log ₂ n , que es indudablemente (asintóticamente) menor que el mismo indicador para una red con Celular (O (√ n )) o Lineal ( O ( n )) topología.

Los dos tipos más simples de redes logarítmicas
Utilizando redes "en forma de árbol" como bloques de construcción, no es difícil generalizar la solución anterior al caso cuando hay más de un punto de partida, pero:k . Hay dos formas fáciles de hacer esto.

La primera forma es utilizar el árbol de Dirección inversa para recopilar primero las rutas de todos los viajes en una secuencia común, y luego, utilizando el árbol de Dirección directa, dividir esta secuencia en subflujos, cada uno dirigido a su destino (red en la parte superior en la Fig. 11 )


fig. 11

Si k y n son potencias de dos, entonces, al final, cualquier ruta pasa exactamente a través de log ₂ k + log ₂ n nodos de conmutación. Redes construidas de acuerdo con el algoritmo que acabamos de describir, acordamos llamar a Logarithmic (unidireccional) con fusión preliminar .

La segunda forma de resolver el mismo problema se puede obtener invirtiendo en la primera solución el orden de las operaciones de fusión y separación. Su implementación es la siguiente: para cada punto de partida, cree un conjunto único de duplicados imaginarios de todos los puntos de dirección de finalización, y luego conéctelo a estos duplicados (ya no imaginarios) con un árbol de Dirección directo.

Para completar la construcción de la red, solo queda conectar ahora cada punto final con un árbol de direcciones inverso con k duplicados imaginarios (la red desde abajo en la Fig. 11).

Siempre que n y k sean potencias de dos, el número de nodos de conmutación en la ruta de cualquier ruta dentro de la red recién construida será nuevamente igual a log ₂ k + log ₂ n . Acordamos llamar a redes de este tipo (unidireccionales) logarítmicas con separación preliminar .

Transformación de redes unidireccionales en simétricas
En general, redes unidireccionalesllamaremos a cualquier red si los puntos de dirección conectados por ella se dividen estrictamente en inicio y fin. Por defecto, para redes unidireccionales, se supondrá que proporciona al menos una ruta de posible movimiento desde cualquier punto de partida a cualquier punto de llegada.

Además de un viaje de por vida, es difícil citar ejemplos en los que cuando algunos puntos de dirección servirían como rutas solo al principio, y otros, solo podrían ser su final. Acercaremos nuestro razonamiento a la realidad si también incluimos redes en las cuales dos puntos de dirección están conectados por rutas en ambas direcciones. Acordamos llamar simétricas a dichas redes .

De hecho, no existe una brecha ideológica entre las redes unidireccionales y simétricas: cada red simétrica también se puede utilizar como una red unidireccional, y cada red unidireccional, que conecta inicialmente un número igual de puntos de inicio y finalización, se puede transformar en una simétrica (Fig. 12).


fig. 12

Las figuras 13a y 13b muestran las formas "simétricas" de la red logarítmica con fusión preliminar y la red logarítmica con separación preliminar. Sus ejemplos muestran la posibilidad fundamental de conectar n bloques con este tipo de red, dentro de la cual el número de nodos de conmutación visitados durante cualquier viaje será proporcional al logaritmo del número de bloques en la ciudad.


fig. 13 a


fig. 13 b

Estimación precisa del fondo
Hasta la fecha, ya se ha acumulado una rica colección de redes con varias funciones, dependiendo del número promedio de nodos visitados durante el viaje en el número de puntos de dirección en la ciudad. Sin embargo, todavía no sabemos cuán pequeño puede ser este número en principio para un número determinado de trimestres. El límite inferior para su valor se puede obtener utilizando el enfoque de información.

En realidad, incluso si una determinada red de carreteras conecta n puntos de dirección, y las necesidades de migración de la población son tales que cualquier viaje, sin importar dónde comenzó, tiene las mismas posibilidades de terminar en cualquier lugar de la ciudad.

Para resolver el problema previsto, generaremos un mensaje informativo auxiliar, siguiendo esta receta: durante un largo período de tiempo, recopilaremos registros de todos los viajes que tienen un punto fijo al principio, y en orden aleatorio anotaremos las direcciones en las que terminaron estos viajes. El mensaje resultante será una secuencia aleatoria compuesta por los nombres de n puntos de dirección de la ciudad.

Una forma de transmitir este mensaje a Marte es primero codificar todos los nombres con palabras binarias de la misma longitud, convirtiendo el mensaje original en una secuencia de ceros y unos, y solo luego enviar la secuencia resultante a través de un canal de comunicación digital. Dado que para la codificación distinguible el conjunto nSi se requieren nombres binarios de longitud log ₂ n , la longitud del mensaje digital será:

(número de registros) × log ₂ n caracteres.

Lo más interesante es que, según la teoría de la información, independientemente del algoritmo de codificación utilizado, es simplemente imposible transmitir el mismo mensaje en promedio con un número menor de caracteres binarios.

Una alternativa a la transmisión directa de los nombres codificados de los puntos finales puede ser un método en el que para cada viaje se indique en cuál de las posibles direcciones giró su ruta en la siguiente bifurcación de la carretera. Según nuestras suposiciones, todas las bifurcaciones en la red solo pueden ser dobles, por lo tanto, para indicar la dirección en cada caso, se requiere exactamente 1 bit. Cualquiera que tenga un mapa de la ciudad y conozca el punto de partida, la cadena de bits adoptada será suficiente para rastrear cada ruta y restaurar la secuencia original de sus destinos. Si el número promedio de bifurcaciones (nodos de división) visitados durante un viaje es x , entonces la longitud del mensaje binario con el nuevo método de codificación será: (número de registros) × x.

Como se dijo anteriormente, un nuevo método de codificación no puede ser más eficiente que el método de transferencia directa de direcciones binarias, por lo tanto: (número de registros) × x ≥ (número de registros) × log ₂ n , de donde:

x ≥ log ₂ n .

Aunque la última desigualdad se dedujo inicialmente para un grupo de viajes que tenían un punto de partida fijo común, su apariencia resultó ser independiente de la elección específica de este punto, por lo que tenemos el derecho de extender el resultado inmediatamente a todos los viajes en la ciudad, obteniendo así la primera parte de la estimación deseada:

P1 ) Siempre que cada nuevo viaje tenga las mismas posibilidades de terminar en cualquiera de nEn los puntos de dirección de la ciudad, el número promedio de nodos divisores por ruta no puede ser menor que log ₂ n .

Haciendo retroceder mentalmente el reloj, hará que cada punto final del viaje sea el punto de partida y que cada nodo de división de red binaria sea un nodo de fusión binario. Este pequeño truco le permite obtener automáticamente la segunda parte faltante de la estimación de P1:

P2 ) Siempre que cada viaje completado tenga las mismas posibilidades de comenzar en cualquiera de los n puntos de dirección de la ciudad, el número promedio de nodos de fusión por ruta no puede ser inferior al registro ₂ n .

Si recordamos la existencia de una red logarítmica con fusión preliminar y una red logarítmica con separación preliminar, inmediatamente obtenemos dos ejemplos de redes que son óptimas en términos del número de nodos de conmutación, que, en promedio, se visitan dentro de ellos durante un viaje. Veamos si esta calidad les ayuda a reducir la intensidad de las pérdidas de conmutación generadas.

Costos de cambio en redes logarítmicas

Si comparamos las redes con la fusión preliminar y la separación preliminar, entonces la primera parece mucho más atractiva debido a su simplicidad. Desafortunadamente, esta simplicidad también tiene un lado negativo de la moneda: la combinación de todas las rutas en un flujo contradice la recomendación i1 , convirtiéndose en una posible causa de grandes pérdidas de tiempo. Una red con separación preliminar parece seguir las recomendaciones i1 - i3 , sin embargo, a juzgar por la Figura 13b, tiende a aumentar rápidamente el número de costillas de carretera y nodos de conmutación utilizados. La última calidad puede hacer que las redes de este tipo sean demasiado caras para un uso práctico.

Analizaremos estos problemas con más detalle. Para comenzar, estamos de acuerdo en que la ciudad está sujeta al modelo de migración de acceso uniforme, y el flujo de viaje generado por cualquiera de sus puntos de dirección tiene una capacidad unitaria.

Pérdidas en una red con fusión preliminar
En la Figura 14 puede ver un diagrama de flujos que surgen de los arreglos indicados dentro de la red con fusión preliminar.


fig. 14

Me pareció conveniente representar la red en su forma unidireccional, lo que implica que cada punto de inicio y finalización, no firmado con los mismos números, de hecho significa el mismo punto de dirección en la ciudad.

Según el diagrama, calculamos la intensidad de los costos de conmutación generados en la red. Comencemos con la mitad izquierda, donde a través del árbol de Dirección inversa, todas las rutas se recopilan en una secuencia. Cada nodo de conmutación en esta parte de la red representa el lugar donde dos carreteras unidireccionales se fusionan en una (Fig. 15).


fig. 15

Si inicialmente cada una de las carreteras se carga de manera eficiente, entonces, después de su unificación, no hay necesidad de reducir el número de carriles, como resultado, no debería haber costos asociados para reducir los costos de cambio.

Suponga que un flujo de potencia de la unidad ya es suficiente para llenar efectivamente el camino en al menos dos carriles. En este caso, llegamos a una conclusión bastante inesperada: la combinación de los flujos de automóviles dentro de la red logarítmica con la fusión preliminar ocurre absolutamente "gratis", sin causar pérdidas temporales.

Calcular los costos que surgen en la mitad derecha correcta no es mucho más difícil. Esta parte de la red es un árbol de direcciones directo, cada nodo del cual es una bifurcación simétrica en las carreteras que ya hemos estudiado. Cuando el poder del ataque de la corriente p intensidad emergente por la pérdida tenedor es igual a ( α / 2 ν ) ⋅ p ² /2. El poder de la corriente que ingresa a la bifurcación raíz es: n , por lo tanto, la intensidad de las pérdidas en el nodo raíz es: ( α / 2 ν ) ⋅ n ²/ 2. En cada próxima generación del árbol de direcciones, el número de horquillas se duplica y la potencia de la transmisión que se ejecuta en ellos se reduce a la mitad. Como resultado, la fórmula de pérdida dentro del árbol completo tomará la forma:

I _{t_div1} = ( α / 2 ν ) ⋅ (1/2) ⋅ [ n ² + 2 ( n / 2) ² + 4 ( n / 4) ² + ... + ( n / 2) ⋅ 2 ² ] =

( α / 2 ν ) ⋅ ( n / 2) ² [1 + 1/2 + 1/4 + ... + 2 /n ] ≈ ( α / 2 ν ) ⋅ n ²

Dado que la potencia del flujo de viaje generado conjuntamente por todos los puntos de dirección es n , los costos de tiempo por viaje son en promedio ( α / 2 ν ) ⋅ n , mostrando así un lineal dependencia del tamaño de la ciudad.

Cuando se trata de redes abstractas, es difícil dar una estimación significativa del área de las carreteras que utilizan. Como una medida alternativa de la complejidad estructural, se puede calcular la potencia total de todos los flujos laterales. Según lo planeado, el valor resultante debe reflejar el costo de los recursos para construir todos los intercambios requeridos por la red. No puedo decir que en la práctica este método siempre tendrá una buena interpretación, pero probablemente pueda tener una idea aproximada de la cantidad de trabajo por delante.

Dentro de la red logarítmica con fusión preliminar, los flujos laterales están presentes solo en el árbol Directo de direcciones, y su potencia total para cada generación de nodos es la misma: n / 2. Registro total de árboles ₂ ngeneraciones de nodos, por lo que una nueva forma de evaluar la complejidad proporciona una estimación de la complejidad: O ( n log ₂ n ).

Red logarítmica con fusión preliminar
Número de puntos de dirección de la unidad de potencia ........................................ ............ n
Tiempo de viaje promedio
perdido debido a los costos de cambio:
comportamiento asintótico ........................ .................................................. ............................ O ( n )
valor exacto ................ .................................................. ........................... ( α / 2 ν ) ⋅ n
El número de nodos de conmutación ............................................... .................................. O ( n )
El número de nodos de conmutación teniendo en cuenta la potencia de los flujos laterales ... ............... O ( n log ₂ n )

Pérdidas en la red con separación preliminar
Pasemos ahora al análisis de la red logarítmica con separación preliminar, suponiendo nuevamente que la red se utiliza para conectar puntos de dirección de la unidad de alimentación. en la ciudad de "acceso uniforme".

La figura 16 muestra un fragmento del mismo, que consta de un punto de dirección junto con árboles de dirección directos e inversos adyacentes a este punto.


fig. 16

En primer lugar, estimamos la intensidad de las pérdidas de conmutación generadas por el fragmento.
Los costos incurridos en la división de los flujos se pueden encontrar sustituyendo en la fórmula I _{t_div1} = ( α / 2 ν ) ⋅ n ² , derivada para el árbol de Dirección directa en el ejemplo anterior, en lugar de n - uno. De hecho, los árboles de Dirección directa en las Figuras 16 y 14 tienen la misma profundidad y conducen flujos similares en grosor a lo largo de ellos mismos ( _{aprox.similitud significa la capacidad de obtener un conjunto de valores multiplicando los valores de otro conjunto por algún número fijo, para ilustrar, se puede utilizar la similitud entre triángulos en sus lados} ). Debido a la dependencia cuadrática entre el valor de los costos de conmutación que surgen en una bifurcación separada y la potencia del flujo que se le suministra, una disminución simultánea en todos los flujos en n veces reducirá las pérdidas en todo el árbol en n ² veces, por lo tanto, en lugar del antiguo ( α / 2 ν ) ⋅ n ² nosotros obtenemos un valor igual a:

I _{t_div2} = ( α / 2 ν ).

Ahora calculamos el valor de los costos en la mitad izquierda del fragmento.
Debido a la pequeñez de los flujos combinados de la carretera dentro del árbol de Dirección inversa, esta vez no sería razonable construir más de dos carriles. Las fusiones en estas condiciones ya no son gratuitas: en contraste con el ejemplo anterior, hay puntos de estrechamiento en la carretera (Fig. 17), donde será necesario cambiar los costos.


fig. 17

Suponiendo que el conductor está al tanto del próximo estrechamiento anticipado, podemos suponer que el proceso de mover automóviles desde el callejón sin salida es lento y se extiende cientos de metros a lo largo de la carretera. En este caso, tenemos derecho a recurrir al truco que utilizamos anteriormente para calcular las pérdidas en la bifurcación simétrica: dividir el flujo de migración total q en muchas partes pequeñas q _i , y luego interpretar cada una de ellas como una corriente lateral desde el lado de la rampa. Las pérdidas generadas por cada subcorriente se calculan mediante la fórmula:
I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s), sin embargo, hay dos sutilezas.

El primero de ellos es que los automóviles no migrarán más allá de la siguiente fila.
Y de hecho: los flujos en los dos carriles centrales, debido a la simetría obvia, siempre deben tener aproximadamente la misma densidad, por lo que los conductores no tendrán muchas razones para cruzar la línea media. De la observación realizada, se deduce que en la fórmula para pérdidas causadas por flujo lateral parcial, s es igual a 1.

A medida que las máquinas abandonan los carriles extremos, reorganizándose en dos filas centrales, la potencia de flujo dentro de las bandas centrales crece gradualmente, cambiando en cada caso de P / 2 a P . Por lo tanto, la segunda sutileza es una dependencia significativa de pa partir del número de subcorriente i , que nos obliga a escribir no:

I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s ),
sino:
I _i = ( α / 2 ν ) p ( i ) ⋅ q _i ⋅ (1 + 1 / s ).
En el caso de que muchas partes pequeñas en las que se dividió el flujo de migración fueran todas del mismo tamaño, la dependencia p ( i ) se expresa mediante un gráfico lineal (Fig. 18)


fig. 18 años

Para calcular la intensidad de las pérdidas totales, uno debe recurrir a la integración o (esto hace posible hacer una forma particularmente simple de una función integrable) como p ( i ) toma el valor promedio en el gráfico igual a 3 P / 4. Puesto que el flujo de migración total de cada extremidad de la banda es P / 2, las pérdidas de intensidad en una fusión nodo separado será:

I _fusionar = 2 ⋅ ( α / 2 ν ) ⋅ (3 P / 4) ⋅ ( P / 2) =

= ( α / 2 ν ) 3 P ²/ 4.

Para encontrar una pérdida temporal generada en una pista en el árbol de dirección inversa es aplicable a la fórmula I _{de combinación} para cada nodo que:

I _{t_merge} = (3/4) ⋅ ( α / 2 ν ) [1 ⋅ (1/2) ² + 2 ⋅ (1/4) ² + 4 ⋅ (1/8) ² + ... + ( n / 2) ⋅ (1 / n ) ² ] ≈

≈ (3/4) ⋅ ( α / 2 ν ) [1/4 + 1/8 + 1/16 + ...] =

= (3/8)⋅ ( α / 2 ν ) [1/2 + 1/4 + 1/8 + ...] =

= (3/8) ⋅ ( α / 2 ν ).

Los costos totales incurridos dentro del fragmento debido a la fusión y separación de flujos serán:

I _{t_merge} + I _{t_div2} = ( α / 2 ν ) [1 + 3/8] = 11/8 ( α / 2 ν ).

Una red logarítmica dividida preliminar contiene solo n fragmentos de este tipo, y exactamente nlos flujos unitarios se generan por sus puntos de dirección, por lo tanto, el valor que acabamos de encontrar es igual a las pérdidas de conmutación que ocurren en promedio por viaje.

De hecho, es más importante para nosotros ni siquiera un número específico, que es igual a los costos de cambio específicos, sino el hecho de que estos costos permanecen constantes al aumentar n . La última circunstancia hace que la red logarítmica con separación preliminar asintóticamente sea la más económica con respecto a las pérdidas de conmutación, entre todos los tipos de redes que estudiamos anteriormente.

Desafortunadamente, el liderazgo no cuesta "gratis". A pesar del tamaño extremadamente pequeño del abrumador número de flujos, cada árbol de direcciones incluido en la red contiene aproximadamente 2 ncostillas de carretera de dos carriles y aproximadamente n nodos de conmutación de tamaño completo. Hay 2 n árboles en la red , lo que significa O ( n ² ) bordes y nodos, lo que lo hace no solo el más económico en el tiempo, sino también la red más costosa de construir, entre todos los ejemplos considerados.

En cuanto a la suma de los flujos laterales, su valor, como es fácil de calcular, crece con la velocidad O ( n log2 n ) y en este caso no tiene mucho significado.

Red logarítmica con separación preliminar
Número de puntos de dirección de la unidad de potencia ........................................ ............ n
Tiempo promedio de viaje,
perdido debido a los costos de cambio:
asintóticos .......................................... .................................................. .......... O (1)
valor exacto .................................. .................................................. ........... 11/8 ( α / 2 ν ).
El número de nodos de conmutación ............................................... .................................. O ( n ² )
El número de nodos de conmutación teniendo en cuenta la potencia de los flujos laterales ... ................ O ( n log ₂ n )

Red logarítmica balanceada

Las pérdidas de conmutación excepcionalmente pequeñas, con el posible uso de la red logarítmica con separación preliminar, pero al mismo tiempo demasiado intensiva en recursos para su construcción, provocan el deseo de encontrar alguna forma de cambiar su diseño para que el consumo de recursos se reduzca significativamente y los costos de conmutación no aumenten significativamente.

Obviamente, el principal culpable de un número excesivamente grande de carreteras en la red es la eficiencia extremadamente baja de su uso. Esto último se puede ver claramente en la Figura 19, que muestra un diagrama detallado de flujos dentro de un árbol de Dirección directa adyacente al i- ésimo punto de dirección.


fig. 19

En el diagrama, el número que se encuentra sobre el borde del árbol denota la potencia de la secuencia de viaje que pasa a lo largo del borde, y el siguiente intervalo es el conjunto de puntos de dirección entre los cuales esta secuencia finalmente se distribuirá. Se cree que todos los bordes presentes en el diagrama son carreteras de dos carriles, el número de bordes en cada generación del árbol se indica en la parte inferior de la figura.

En una inspección más cercana, puede observar que la regla por la cual el flujo de viaje se divide en un nodo particular está determinada únicamente por la posición de este nodo dentro del Árbol de direcciones y no depende del número del punto de dirección que dio lugar a estos viajes.

Si hay varias corrientes dirigidas al mismo conjunto de puntos, y cada una de ellas no es lo suficientemente potente como para llenar su ruta asignada, entonces, ¿por qué no combinarlas en una carretera? De hecho, esta idea esencialmente simple hace posible construir una buena red abstracta, generando pérdidas de conmutación relativamente pequeñas y económica en la cantidad de caminos utilizados.

Volviendo al árbol de direcciones del i- ésimo punto, vemos que la secuencia que ingresa al nodo raíz se divide en dos secuencias secundarias con una capacidad de 1/2 cada una. La primera secuencia de stepson consiste en viajes dirigidos a puntos del intervalo [1; n / 2], el segundo - viajes dirigidos a puntos del intervalo [( n / 2) + 1;n ].
Siguiendo la idea descrita anteriormente, combinamos el mismo tipo de flujos de hijastros en cada punto impar y el siguiente punto de dirección con un número par que lo sigue en orden. Dicha técnica permite que cada par de puntos seleccionados tenga en lugar de cuatro corrientes con una potencia de 1/2 solo dos corrientes de magnitud unitaria (Figura 20). Le daremos la abreviatura BN ₂ [i; i +1].


fig. 20

Si los flujos de hijastros no se combinaran, pero aún estuvieran dentro del árbol de Dirección, entonces en la próxima generación de nodos alcanzados, cada uno de ellos se dividiría nuevamente en dos partes, iguales en potencia y en el tamaño de los conjuntos de esos puntos a los que componentes de sus viajes.

¿Por qué romper la tradición establecida, porque después de la unificación todavía tenemos el mismo conjunto de tipos de flujo que antes, pero con solo menos representantes de cada tipo? - aplicable a cada uno de los flujos de salida BN ₂ [i; i +1] exactamente la misma regla de separación que se aplicaría a una secuencia de este tipo dentro del árbol de direcciones.

No hay ninguna razón por la cual la construcción lógica descrita anteriormente para combinar-dividir los mismos flujos no pueda repetirse inductivamente. La figura 21 muestra un diagrama de combinación de dos fragmentos de
BN ₂ en un fragmento de BN ₄ , y la figura 22 muestra cómo se ve el algoritmo en el caso general.


fig. 21


fig. 22

Al final, el proceso de ampliación de la fragmentación se completará y nos llevará al único elemento BN _n [1; n ], lo llamaremos la red equilibrada del tipo logarítmico (Fig. 23).


fig. 23

Examinemos esta red por la complejidad y magnitud de las pérdidas de conmutación generadas.
Según la naturaleza inductiva del procedimiento de construcción de la Red equilibrada, la ecuación de retorno puede describir el número de nodos de conmutación incluidos en su estructura:

nodos (BN _k ) = 2 nodos (BN _{k / 2} ) + 2 k ,

con condición límite:

nodos (BN ₁ ) = 0.

La solución a este sistema de ecuaciones es la función:

nodos (BN _n ) = 2 n log ₂ n .

Dado que la construcción de BN _n requiere log ₂ n pasos de inducción, cada viaje pasará por log ₂ n nodos de separación y el mismo número de nodos de fusión, alternando en su camino (Fig. 24).


fig. 24

Pérdidas generadas dentro de cada nodo de separación:
( α / 2 ν ) ⋅ (1) 2/2 .

Pérdidas generadas dentro de cada nodo de fusión:
( α / 2 ν ) ⋅ 3 ⋅ (1/2) 2/4 = 3/16 ( α / 2 ν ).

Dado que ambos en la Red equilibrada son n log ₂ n , obtenemos el valor exacto de las pérdidas de conmutación totales:
11/16 ( α / 2 ν ) n log ₂ n ,

que por un viaje es:
11/16 ( α / 2 ν ) log ₂ n

Red logarítmica balanceada
El número de puntos de dirección de alimentación de la unidad ............................................. ....... n
Tiempo de viaje promedio
perdido debido a los costos de cambio:
asintóticas ................................................. .................................................. ... O (log ₂ n )
valor exacto ................................................ ............................................... 11/16 ( α / 2 ν ) log ₂ n
El número de nodos de conmutación ............................................... .................................. O ( n log ₂ n )
El número de nodos de conmutación, teniendo en cuenta la potencia de los flujos laterales ................... O ( n log ₂ n )

Las cifras encontradas anteriormente permiten que la Red equilibrada se considere un buen compromiso entre la cantidad de pérdida de tiempo introducida y la complejidad estructural general. Su uso como red de carreteras de una ciudad real es en principio posible, pero difícilmente económicamente viable. Me parece que el área donde el uso de la Red Equilibrada puede ser realmente de gran beneficio son los sistemas de información a gran escala con requisitos estrictos para la cantidad de retraso de la señal, como las comunicaciones celulares, Internet, la computación distribuida, las computadoras multiprocesador. Para nosotros, el valor principal de la Red equilibrada es el método por el cual se construyó. Un poco más tarde, utilizando una modificación de este método, podremos mejorar las redes de centros lineales y celulares que son realmente importantes en términos prácticos.

¿Por qué las ciudades históricas están condenadas a atascos?

Mi declaración puede parecer inesperada, pero la respuesta a por qué las ciudades en desarrollo natural, generalmente sufren de atascos de tráfico, ya la encontramos en los párrafos anteriores. Entonces, ¿en qué consiste?

El hecho es que muchas ciudades históricas que sobrevivieron a la era de las fortalezas medievales (por ejemplo, casi todas las capitales del "Viejo Mundo") heredaron de esta época la estructura radial de las calles. Desafortunadamente (para sus residentes modernos), una red de carreteras con una topología similar no escala bien: la ubicación densa de las carreteras radiales cerca del centro se está volviendo demasiado rara en la periferia. Como resultado, en el proceso de crecimiento de la población, las calles que inicialmente se ubicaban al margen de los pocos caminos que conducen a la fortaleza se hicieron más grandes y las calles que aparecían en la periferia eran cortas y no adquirieron suficiente importancia de tránsito para crecer en amplitud. Como resultado, la red de carreteras que vemos ahora en las grandes ciudades históricas se refiere con mayor frecuencia a los sistemas de transporte de tipo Arterial, y en nuestra terminología, al tipo de redes logarítmicas con fusión preliminar (incompleta).


(Carreteras de Moscú, foto: Stepanov Slava)

Si hablamos de la longitud del camino que debe conducir un conductor en las carreteras, entonces la implementación de este tipo de red no es mala: la distancia recorrida a menudo difiere poco de la distancia en línea recta y su valor promedio en la ciudad, como debería ser para los sistemas de transporte "decentes" , crece a una tasa de O (√ n ). El problema es que con la ampliación de la ciudad en la red logarítmica con la fusión preliminar, los costos de cambio generados por ella aumentan demasiado rápido: la cantidad de tiempo por la cual el viaje se extiende en promedio debido a ellos depende de la cantidad de personas que viven en la ciudad como O ( n ) Está claro que a partir de algunos n , esta vez prevalecerá sobre el tiempo despejado para superar la distancia, en otras palabras, aparecerán atascos en la ciudad.

Sin duda, la reorganización del sistema de transporte en las grandes ciudades históricas es una tarea que se puede resolver. Sin embargo, es importante entender aquí que la construcción de otras, dos o cinco arterias de transporte grandes, aunque mejoran ligeramente la situación en la ciudad, pero la causa raíz de los atascos no se eliminará. Aparentemente, la única forma de superar las deficiencias de la red logarítmica con la fusión preliminar es utilizar otra red. Un buen candidato aquí puede ser una red con topologías celulares, para la cual la tasa de crecimiento del tiempo para cubrir la distancia, al menos, coincide con la tasa de crecimiento de las pérdidas de conmutación.


(noche Berlín, foto: Vincent Laforet)

Quizás es por eso que el Berlín moderno, aunque tiene grandes carreteras arteriales, ya se distingue por una estructura de malla claramente visible.

Hay muchas soluciones interesantes en el mundo sobre cómo hacer que los residentes de las ciudades históricas sean más móviles, pero el premio principal en la lucha por la accesibilidad del transporte probablemente debería otorgarse a los ingenieros de Barcelona.


(Red de carreteras actualizada de Barcelona, ​​foto: Vincent Laforet)

Una mirada detallada a las redes de ciudades lineales y celulares

Después de encontrar y refinar los métodos de análisis en redes abstractas, llegó el momento de aplicarlos a casos más realistas de ciudades con topología lineal y celular. En esta sección trataremos de analizar en detalle las características de sus enlaces de transporte, establecer el valor numérico de la intensidad de pérdida de conmutación, descubrir cómo su valor depende del tamaño de los cuartos y discutir posibles variaciones y mejoras.

Ciudad lineal
Esta vez, considere un ejemplo de una ciudad en la que hay dos calles de sentido único: oeste con un movimiento hacia el norte y este con un movimiento hacia el sur (Fig. 25).


fig. 25

Deje que cada trimestre genere una corriente de desplazamiento de la unidad de potencia. En este caso, una ruta de viaje que conduce de una cuadra a otra representa 1 / n de flujo de tráfico.

Definimos para empezar el poder de los flujos laterales en las carreteras de la calle. Occidental
la calle es la única forma de llegar al barrio con el número i desde
( n - i ) cuartos que se encuentran al sur de la misma, y ​​la única forma en que desde el cuarto i es llegar a ( i - 1) cuartos ubicados al norte de la misma. De ello se deduce que la capacidad de los flujos de intercambio de tráfico entre la calle Zapadnaya y el distrito i- ésimo es igual a:

q _{W_out} = ( n - i ) / n - para la corriente lateral que sale de West Street,
q _{W_in} = ( i - 1) / n - para el flujo lateral adyacente al movimiento en él. Está claro que el poder del lado fluye en la calle Vostochnaya depende de i de manera simétrica:
q _{E_out} = ( i - 1) / n es el poder del que se va,
q _{E_in} = ( n - i ) / n es la potencia del flujo lateral adyacente al tráfico en East Street.

Por supuesto, la suma de los flujos que salen del i- ésimo trimestre:

q _{E_in} + q _{W_in} = ( n - 1) / n ,
coincide con la suma de los flujos que ingresan:
q _{E_out} + q _{E_out} = ( n - 1) / n ,
y ambos valores no dependen de i de ninguna manera (cada trimestre tiene un flujo de desplazamiento de 1 / n de magnitud, que comienza y termina dentro de sí mismo).

Para encontrar el poder de los flujos principales, dibujamos una línea imaginaria a través de la Autopista del Oeste en el mismo nivel con el i- ésimo cuarto. En total, esta línea cruzará:
(el número de trimestres desde abajo) × (el número de trimestres desde arriba) = ( n - i ) ( i - 1) de rutas que juntas crean una secuencia con el valor:

P _W ( i ) = ( n - i ) ( i - 1) / n .

La misma formula:
(número de trimestres desde abajo) × (número de trimestres desde arriba) / n ,
debe expresarse y el flujo de tráfico P P en East Street, en otras palabras:

P _E ( i ) = P _W ( i ) = P ( i ).

Conociendo la potencia de todos los flujos principales y secundarios, podemos calcular la intensidad de las pérdidas que ocurren en la red en el área cercana al i- ésimo trimestre:

I ( i ) = ( α / 2 ν ) ⋅ P ( i ) ⋅ [( q _{E_in} + q _{W_in} ) ⋅ (1 + 1 / s ) + ( q _{E_out} + q _{E_out} ) ⋅ (1 - 1 / s )] =
= ( α / 2 ν ) ⋅ P ( i ) ⋅ [(1 - 1 / n ) ⋅ (1 + 1 / s ) + (1 - 1 / n ) ⋅ (1 - 1 / s )] =
= ( α / 2 ν ) ⋅ 2 P ( i ) ⋅ (1 - 1 / n ) =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ( i - 1) / n =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ).

Si sumamos la última expresión sobre i , obtenemos la intensidad de las pérdidas generadas por toda la red en su conjunto.

I = ∑ _i I ( i )
= ∑ _i 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ) =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ n ² ⋅ ∑ _i (1 - i / n ) ⋅ ( i / n - 1 / n ) ⋅ (1 / n ) ≈
≈ 2 ( α / 2 ν ) ⋅ n ² ⋅ ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ).

La suma ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ) se puede reemplazar con la integral con buena precisión por una integral:

∫ t (1 - t ) d t ( t ∈ [0; 1]) = 1/2 - 1/3 = 1/6.

¿Dónde obtenemos que la intensidad de las pérdidas de conmutación en una ciudad lineal con n bloques de capacidad unitaria es:

I = ( α / 2 ν ) n 2/3.

Hasta este momento, consideramos solo ejemplos en los que los trimestres siempre generaban flujos de unidad de potencia. Veamos si la fórmula para las pérdidas de conmutación de la Ciudad lineal cambia si no hay una sola fuente de energía unitaria para cada trimestre, sino - λ (los cuartos se volverán λ veces más grandes).

Toma una ciudad con m cuadras. Si los bloques generaron flujos de potencia 1, entonces las pérdidas de conmutación serían ( α / 2 ν ) m 2/3. Un aumento en el poder de producción de viajes en un factor de λ cada trimestre conduce a un aumento en λ de los flujos principales y secundarios simultáneamente, por lo tanto, los costos en cada intercambio, y por lo tanto dentro de la red en su conjunto, aumentan en un factor de ² , y la fórmula de pérdida toma la forma:

I = ( α / 2 ν ) m ² ⋅ λ 2/3 .

En general, no importa en absoluto cómo las pérdidas de conmutación dependen del número de barrios de la ciudad, lo principal para nosotros es cómo dependen del flujo de energía de todos los viajes generados en su interior, o en otras palabras, del número n de fuentes de energía de la unidad. En el caso considerado, n es igual a m ⋅ λ , por lo tanto:

I = ( α / 2 ν ) m ² ⋅ λ 2/3 =
= ( α / 2 ν ) ( m ⋅ λ ) 2/3 =
= ( α / 2 ν ) n 2/3.

En otras palabras, las pérdidas de cambio en la Ciudad Lineal no dependen de la pequeñez de su división en barrios.

Ciudad celular
Imagine una ciudad celular en la que los caminos de calles perpendiculares están espaciados en altura en diferentes niveles. Esto es posible, por ejemplo, si todas las calles que conducen de norte a sur se elevan sobre puentes, y las carreteras que se extienden de oeste a este se construyen en la superficie de la tierra. Si, además, todas las calles tienen tráfico en ambos sentidos, la hoja de ruta en dicha ciudad se referirá a la Topología celular estándar (Fig. 26).

El punto aquí, por supuesto, no es llevar a la práctica la red descrita anteriormente: no se vería demasiado estéticamente agradable en el contexto del paisaje de la ciudad y, además, debido a la necesidad de intercambios de varios niveles, consumiría una buena mitad del espacio de la calle. Sin embargo, esta red puramente hipotética es una buena manera de obtener las estimaciones necesarias, que luego pueden extenderse fácilmente a redes de carreteras que son realmente interesantes desde el punto de vista de su aplicabilidad en ciudades reales.

Como de costumbre, asumiremos que las necesidades migratorias de los residentes se describen mediante el modelo de "acceso uniforme", y comenzaremos a considerar el caso cuando la capacidad de todos los flujos de viaje generados por un trimestre separado sea 1.

En el ejemplo con la Ciudad Celular Estándar, es conveniente alejarse de la tradición establecida y considerar el punto de dirección no como un barrio separado, sino como una zona territorial de forma cuadrada, que captura la intersección de las carreteras de la calle y un cuarto de todos los vecindarios adyacentes. La Figura 27 muestra el posicionamiento relativo de varias de esas zonas y muestra un patrón de tráfico dentro de una de ellas. Este diagrama muestra claramente que cualquier conductor, que abandona el trimestre, tiene la oportunidad de subir a la autopista y moverse en dirección a cualquiera de las cuatro partes del mundo.


fig. 26

Para encontrar el valor de los costos de cambio generados por la ciudad, calculamos la potencia de todos los flujos principales y secundarios dentro de cada una de sus zonas territoriales. La forma y la disposición mutua de las zonas nos permiten recurrir a una analogía del ajedrez para resolver el último problema, considerando las zonas como celdas del campo y el movimiento de los automóviles entre ellas: los movimientos del bote (Fig. 27). De una celda a otra, siempre que estén en una "posición general" entre sí, la torre se puede mover en dos movimientos, y si ambas celdas se encuentran en la misma horizontal o vertical, entonces en una.


fig. 27

Para evitar muchas reservas inconvenientes, asumimos que el movimiento en el que la torre no se mueve a ningún lado también está permitido de acuerdo con nuestras reglas. La ruta de movimiento de la torre, que consta de dos movimientos, uno de los cuales se realiza necesariamente verticalmente y el otro horizontalmente, se llama el más simple. Es razonable considerar el movimiento "en su lugar" tanto vertical como horizontal al mismo tiempo. En este caso, la afirmación es cierta de que dos celdas del tablero están conectadas entre sí por exactamente dos rutas más simples diferentes.

Para los conductores, la ruta "más simple" es la forma más fácil de llegar con una mínima interferencia de una zona territorial a otra, por lo que es razonable suponer que se realizarán viajes reales a lo largo de líneas de ruta elementales. Según el modelo de "acceso uniforme" generado por el punto de dirección (zona territorial), el flujo de energía de la unidad debe distribuirse equitativamente entre todos los puntos de dirección n = d ² de la ciudad, por lo tanto, la capacidad del flujo de viaje que viaja a lo largo de una línea de ruta es 1 / (2 n ).

Calculamos el flujo de qué magnitud pasa a través de la celda ( i , j ) en la dirección de sur a norte. La ruta más simple cruza la celda ( i , j ) de sur a norte en solo dos situaciones. El primero de ellos (Fig. 28 a la izquierda):

1a) la celda inicial de la ruta se encuentra en una de las últimas ( d - i ) líneas de contorno (líneas);
2a) el punto final de la ruta es una de las primeras ( i - 1) celdas de la j- ésima vertical (columna);
3a) la ruta comienza con una sección horizontal, o se encuentra completamente dentro de la columna j .


fig. 28

Las condiciones que describen la segunda situación parecen simétricas (Fig. 28 a la derecha):

1b) el punto de partida de la ruta es una de las últimas ( d - i ) celdas de la vertical enésima ;
2b) la celda final de la ruta está en uno de los primeros contornos ( i - 1)
3b) la ruta comienza con una sección vertical, o se encuentra completamente dentro de la columna j .

En el tablero de ajedrez solo hay 2 × [ d ⋅ ( i - 1) + 1 ⋅ ( i - 1)] × ( d - i ) adecuado para los requisitos de las rutas más simples, que juntas crean un flujo de energía:

P _SN ( i , j ) = ( d + 1) ⋅ ( i - 1) ⋅ ( d - i ) / n (= P _SN ( i )).

Arreglando j , obtenemos la función

( P _SN ) _j ( i ) = P _SN ( i , j = Const),

describiendo la dependencia del poder de la corriente que se mueve hacia el norte a lo largo de la enésima autopista vertical, en la distancia al límite superior de la ciudad, medida en celdas.
Hay varias observaciones más o menos obvias con respecto a las funciones ( P _SN ) _j ( i ), hablemos de ellas.

Comenzamos, quizás, con una circunstancia que sería difícil pasar por alto: P _SN ( i , j ) es en realidad independiente del segundo argumento. Como resultado, las funciones ( P _SN ) _j ( i ) = P _SN ( i ) tienen la misma forma para todos los valores de j , en otras palabras, la posición específica de la calle dentro de la Ciudad Celular no afecta su carga. Formalmente, la última declaración se prueba solo para la carretera que conduce al norte, pero debido a las simetrías de la ciudad, también se extiende automáticamente a la carretera de otras direcciones.

Ahora veamos la fórmula misma para P _SN ( i ):

( d + 1) ⋅ ( i - 1) ⋅ ( d - i ) / (2 n ).

Como vemos, toda la dependencia de P _SN de i radica en la expresión ( i - 1) ⋅ ( d - i ). Esta expresión puede interpretarse como el producto de las longitudes de los intervalos derecho e izquierdo en los que el segmento entero de longitud d se divide después de que el i- ésimo elemento se elimina de él (Fig. 29a).


fig. 29a


fig. 29b

Está claro que si cambia "derecha" a "izquierda" e "izquierda" a "derecha" (Fig. 29b), el resultado del trabajo seguirá siendo el mismo. De una observación tan simple, en esencia, hay dos conclusiones que nos son muy útiles:

1. la función P _SN ( i ) es simétrica con respecto al punto medio de la calle i = ( d + 1) / 2, en otras palabras, la potencia de flujo a una distancia Δ del límite inferior de la ciudad es exactamente la misma que a una distancia Δ del límite superior.
2. En general, la ciudad en sí es simétrica hacia arriba y hacia abajo, por lo tanto, para obtener la función ( P _NS ) _j ( i ), que describe el flujo de energía en la carretera j- ésima, pero en dirección sur, es suficiente simplemente reflejar el gráfico de función ( P _SN ) _j ( i ) en la línea i = ( d + 1) / 2. Dado que ( P _SN ) _j ( i ) = P _SN ( i ), y la gráfica de P _SN ( i ) con respecto a la línea i = ( d + 1) / 2 es simétrica, entonces ( P _NS ) _j ( i ) = P _SN ( i ) = P _vert ( i ), en otras palabras, los flujos de tráfico directos e inminentes tienen la misma potencia en cualquier lugar de la ciudad. En la Figura 30 se muestra un gráfico aproximado de P _SN ( i ) (se cree que d >> 1, i >> 1, d - i >> 1).

fig. 30

Las potencias de los flujos principales a lo largo de las carreteras horizontales se encuentran fácilmente utilizando simetrías rotacionales; formalmente, este proceso se reduce a un simple reemplazo de i por j en P _SN ( i ) y una versión pequeña del índice inferior.

Lo siguiente que debe hacer es encontrar el poder de los flujos laterales. Los viajes que entran o salen del tráfico en una carretera vertical dentro de la celda ( i , j ) se pueden dividir convenientemente en cuatro categorías:

1. q _{in_transit} : — i - , — j - , ( i , j ) ( 31a);
2. q _{out_transit} : — j - , ( i , j ), — i - ( 31b);
3. q _in : — ( i , j ), — i - ( 31c);
4. q _out : — i - . — ( i , j ) ( 31d).

fig. 32: abcd

Contando el número de líneas de ruta que pertenecen a cada categoría separada, concluimos que las potencias de las cuatro corrientes son iguales e iguales:

q ₀ = d ⋅ ( d - 1) / (2 n )

Tener los valores de las potencias de los flujos principales y laterales En una carretera vertical, no es difícil calcular la cantidad de costos derivados de su cambio. Dentro de una sola celda ( i , j ), los costos serán iguales a:

I _vert ( i , j ) = ( α / 2 ν ) ⋅ P _vert( i ) ⋅ [( q _in + q _{in_transit} ) ⋅ (1 + 1 / s ) + ( q _out + q _{out_transit} ) ⋅ (1 - 1 / s )]
= 4 ( α / 2 ν ) ⋅ ( d + 1) ( i - 1) ( d - i ) ⋅ d ( d - 1) / 2 n ² ≈
≈ 2 ( α / 2 ν) ⋅ d ⁵ ⋅ ( i / d ) (1 - i / d ) ⋅ (1 / d ) ⁴ =
= 2 ( α / 2 ν ) ⋅ d ² ⋅ ( i / d ) (1 - i / d ) ⋅ (1 / d ).

Para encontrar los costos incurridos en calles verticales dentro de toda la ciudad, necesitamos sumar I _vert ( i , j) para ambos índices:

I _vert = ∑ _ij I _vert ( i , j ) =
2 ( α / 2 ν ) ⋅ d ² ⋅ ∑ _ij ( i / d ) (1 - i / d ) ⋅ (1 / d ) .

Dado que la magnitud de los términos no depende de j de ninguna manera , sumar sobre el segundo índice es equivalente a multiplicar por d :

∑ _ij ( i / d) (1 - i / d ) ⋅ (1 / d ) = d ⋅ ∑ _i ( i / d ) (1 - i / d ) ⋅ (1 / d ).

La última suma puede ser aproximada por la integral que ya nos es familiar:

∑ _i ( i / d ) (1 - i / d ) ⋅ (1 / d ) ≈ ∫ t (1 - t ) d t ( t∈ [0; 1]) = 1/2 - 1/3 = 1/6.

Lo que implica que

I _vert = ( α / 2 nu ) ⋅ d ³ /3 = ( α / 2 nu ) ⋅ n √ n / 3.

Cuando se le preguntó cuál es el nivel de los costes de I _Horiz , que se producen en la carretera horizontal, la ciudad utilizando la simetría puede responder:

I _horiz = I _vert = ( α / 2 ν ) ⋅ n √ n / 3.

Por lo tanto, la intensidad de las pérdidas de conmutación dentro de toda la red de la Ciudad Celular Estándar es:

I = I _vert + I _horiz = 2/3 ⋅ ( α / 2 ν ) ⋅ n √ n ,

y el costo promedio por viaje es

2/3 ⋅ ( α / 2 ν ) ⋅ √ n

Efecto del tamaño de la celda sobre el valor de las pérdidas de conmutación
Los trimestres que generan flujos de potencia unitaria son una limitación bastante artificial de las condiciones del problema. Extendemos los resultados obtenidos anteriormente a los casos en que la potencia del flujo de viaje generado por una celda territorial es igual a λ .
Deje que la ciudad consista en m de tales celdas. Si todas las celdas tuvieran solo una unidad de potencia, entonces la intensidad de las pérdidas de conmutación totales sería I ₁ = 2/3 ⋅ ( α / 2 ν ) ⋅ m √ m . Un aumento en el número de viajes realizados por λ veces en λlos tiempos aumentarán la potencia de todas las corrientes principales y laterales de las carreteras de la calle, lo que a su vez hará que λ ² veces aumente todos los costos de cambio generados dentro de la ciudad. La nueva fórmula para la intensidad de las pérdidas tomará la siguiente forma:

I = 2/3 ⋅ ( α / 2 ν ) λ ² ⋅ m √ m

Si suponemos que la celda consta de puntos de dirección λ de potencia unitaria, entonces el número total de tales puntos será: n = λ m . Expresemos I como una función de n y λ :

I= 2/3 ⋅ ( α / 2 ν ) λ ² ⋅ m √ m =
= 2/3 ⋅ ( α / 2 ν ) ⋅ √ λ ⋅ ( λ √ λ ) ⋅ ( m √ m )
= 2/3 ⋅ √ λ ( α / 2 ν ) ⋅ ( λ m ) √ ( λ m )
= 2/3 ⋅√ λ ( α / 2 ν ) ⋅ n √ n .

El costo promedio por viaje bajo las nuevas condiciones será 2/3 ⋅ √ λ ( α / 2 ν ) ⋅ √ n , siendo √ λ veces mayor que su valor en una ciudad compuesta por cuartos de capacidad unitaria.

La última fórmula nos dice que para la misma población, densidad de población y área total de todas las carreteras, el costo de los costos de cambio es mayor, cuanto mayor sea el trimestre al momento de diseñar la ciudad fue elegido por su arquitecto. En el caso de que la población de la ciudad se distribuya de manera desigual en su territorio, por supuesto, no se debe prestar atención a las dimensiones geométricas, sino principalmente al número promedio de personas dentro del barrio y su actividad migratoria.


(Foto del centro de Nueva York: Vincent Laforet)

La observación anterior es especialmente importante al diseñar áreas con edificios de rascacielos. Debido a la combinación de alta densidad de población y su alta movilidad, es deseable hacer que los cuartos en áreas de gran altitud sean varias veces más pequeños de lo habitual para construir pisos estándar. En las civilizaciones, donde la construcción de rascacielos tiene una larga historia, la práctica de aislar incluso edificios grandes separados como un bloque está muy extendida.

Semáforo Ciudad Celular
En cada caso, cuando las líneas de dos carreteras concurridas se cruzan en el mapa, el arquitecto debe elegir: levantar una de estas carreteras hacia el puente, permitiendo que el flujo de la otra pase libremente desde abajo, o realizar la intersección en forma de una intersección regular y resolver el conflicto de flujo que resulta en tráfico regulación. La segunda opción atrae con su simplicidad, la falta de la necesidad de construir estructuras de ingeniería a gran escala, y además, proporciona una manera fácil de cruzar el camino para los peatones, por estas razones en las ciudades a menudo lo prefieren.


(tarde en el centro de Los Ángeles, foto: Boris Shein)

El uso de semáforos en redes con topología celular tiene sus propias características. En el Capítulo 1, se demostró que con la sincronización adecuada de los semáforos, los automóviles, mientras se mueven por la misma calle, ni siquiera tienen que detenerse en las intersecciones: una luz verde siempre se iluminará en su dirección. Este tipo de fenómeno generalmente se llama régimen de ola verde . Para crearlo, los flujos de tráfico deben dividirse en dos zonas alternas de dos tipos: llenas de automóviles y libres de ellas. A continuación, se selecciona un modo de operación de semáforos que en el período de tiempo en que la siguiente `` porción '' pasa la intersección a lo largo de una de las calles, la porción anterior de automóviles que se mueven a lo largo de la calle perpendicular ya la ha pasado, y la siguiente aún no ha llegado (Fig.33).


fig. 33

La capacidad de conducir el tráfico en el modo verde conlleva sus propios costos e impone ciertas restricciones en el diseño de las calles de la ciudad.

Mirando nuevamente la Figura 33, es fácil ver que en un momento dado no se usa exactamente la mitad del área de todas las carreteras. Para compensar lo simple, en la mitad de la carretera usada, el poder local de los flujos de automóviles y el número de carriles necesarios para ellos debe ser el doble que en una ciudad con pasos elevados.

La segunda circunstancia más importante asociada con el uso de ondas verdes es la estricta regulación del tamaño permitido de los cuartos: su longitud (para calles de dos vías) debe ser un múltiplo de la longitud de la ola verde llena (una sección de la corriente dentro de la cual es posible un movimiento sin obstáculos), que es de unos 500 metros. Como se señaló en el párrafo anterior, las áreas con una alta densidad de población requieren una mayor frecuencia de ubicación de las carreteras, por lo que la restricción desde abajo en la distancia entre las autopistas puede causar dificultades de tráfico.

Es interesante observar que en el modo de ondas verdes, las reglas cambian ligeramente según las rutas de viaje que se cambian dentro de la red. Por ejemplo, la conexión de otro automóvil al flujo de tráfico principal en una carretera de la calle se puede realizar entre las zonas llenas, sin causar costos de cambio serios (punto "1", Fig. 34a).


fig. 34

Por supuesto, este automóvil en sí tendrá que perder algo de tiempo esperando la zona vacía más cercana antes de ingresar a la autopista, y después de eso, permanecer en el semáforo hasta que llegue a la siguiente zona completa (punto "2", Fig. 34a), sin embargo La magnitud de estas pérdidas no depende ni del tamaño de la ciudad ni del ajetreo del tráfico en la calle, por lo que pueden descuidarse a gran escala.

La situación es completamente diferente si un automóvil intenta dejar el tráfico en una carretera de la calle (Fig. 34b). Aquí, con toda probabilidad, ya no hay formas difíciles de hacer que las pérdidas de cambio creadas por él sean menores. Además, debido a la duplicación de la potencia local del flujo dentro de las zonas llenas, la extracción de un automóvil seleccionado arbitrariamente cuesta el tiempo el doble que en una ciudad con pasos elevados. En total, la "entrada" abaratada y la "salida" más cara de los arroyos de la calle se compensan entre sí, lo que hace que Traffic City Cell City a este respecto casi no sea mejor, pero no peor que Standard.

Ciudad celular unidireccional
Además del uso de semáforos, hay al menos una oportunidad más para alejarse de los monstruosos intercambios de la Ciudad Estándar. Consiste en dividir espacialmente (Fig. 35) caminos con la dirección opuesta de movimiento.


fig. 35

Como resultado de tales cambios, el número de calles se duplicará, todas se volverán unilaterales, pero lo más importante, los intercambios se simplificarán enormemente (Fig. 36).


fig. 36
Dado que el número de autopistas que conducen a cada una de las Partes del Mundo, y el número de viajes que pasan por ellos, se mantuvo igual, la capacidad de todos los flujos y, con ellos, los costos de cambio en la Ciudad Celular de Una Vía y la Ciudad Estándar con dos grandes barrios (lineales), deberían emparejar Si comparamos las ciudades Estándar y Unilateral con los mismos cuartos de tamaño, la segunda tendrá el doble de pérdidas por cambio.

Calle "lineal".

¿Cómo se podrían reducir las pérdidas de conmutación en una red celular? La respuesta a esta pregunta nos permitirá seleccionar con éxito una analogía y un poco de comprensión.

Considere una modificación algo inusual de la Red Celular, que implica que todas las carreteras que se extienden de oeste a este son bidireccionales, mientras que en las carreteras perpendiculares a ellas, el tráfico se permite solo en una dirección: norte o sur, y estas direcciones se alternan de calle en calle.

Como siempre, asumiremos que la ciudad obedece el modelo de acceso uniforme, y cada cuarto genera un flujo de viaje de potencia unitaria condicional.

En este caso, parece plausible que el núcleo dentro del cuarto ( i , j) el flujo de viajes, dejándolo, se distribuye entre las calles más cercanas de la siguiente manera: 1/4 de ella llega a la carretera horizontal desde arriba, 1/4 más a la carretera horizontal desde abajo, 1/4 ⋅ i / d fluye hacia el norte a lo largo de la carretera vertical y
1/4 ⋅ (1 - i / d ) - a lo largo de la segunda carretera vertical hacia el sur (Fig. 37).

fig. 37

De hecho, de acuerdo con los algoritmos de construcción de rutas discutidos anteriormente, según las estadísticas, la mitad de los viajes comenzarán desde una sección horizontal, y para los conductores que prefieren esta mitad, en general no debería importar si su ruta se encuentra al norte del trimestre ( i , j ) o al sur de él La mitad restante de los viajes comenzará con una sección vertical de tráfico y se dividirá entre la carretera sur y norte con respecto al número de cuartos que se encuentran ( i , j ) hacia el sur al número de cuartos que se encuentran al norte.

En cuanto al flujo de viaje dirigido hacia adentro ( i , j), entonces la regla de su división con respecto a la carretera que rodea el barrio será simétrica (Fig. 38).


fig. 38

Entre las cuatro intersecciones adyacentes al cuarto ( i , j ), consideramos por separado los flujos laterales en la intersección de la carretera horizontal inferior y la calle vertical con tráfico hacia el norte (Fig. 38). máquina de flujo que entra en una posición horizontal a una vista previa vertical es:
1/2 ⋅ (el número de bloques en el horizontal) x (el número de bloques en vertical no por debajo de ( i , j )) ⋅ 1 / d ² =
= 1/2 ⋅ d ⋅ i / d ² =
= 1/2 ⋅ i / d .
La magnitud de la corriente lateral en la dirección opuesta es:
1/2 ⋅ (el número de bloques en vertical, estrictamente a continuación ( i , j )) x (el número de bloques en vertical) ⋅ 1 / d ² =
= 1/2 ⋅ ( d - i ) ⋅ d / d ² =
= 1/2 ⋅ (1 - i / d ).

Pasemos ahora nuestra atención de la Ciudad Celular en su conjunto a cualquiera de sus calles verticales, llamémosla My_street. Debido a las simetrías, no limitaremos nuestro razonamiento en absoluto, si suponemos que el movimiento a lo largo de My_street se dirige de sur a norte (Fig. 39).


fig. 39

La Figura 40 representa los gráficos de la potencia de los flujos principales y laterales en la carretera a lo largo de My_street, que, como puede notar el lector, son increíblemente similares a gráficos similares para la carretera de sentido único de Linear City (Fig. 26).



fig. 40

En estos ejemplos, los diagramas de flujo coinciden completamente si dentro de My_street los flujos laterales relacionados con cada par de cuartos opuestos y la carretera horizontal debajo de ellos se asignan formalmente a una celda territorial imaginaria. Como se puede ver en las tablas anteriores, la red de carreteras de la Ciudad Lineal genera algunas de las mayores pérdidas de conmutación entre las redes de las arquitecturas que ya hemos estudiado. Desde este punto de vista, el patrón de tráfico dentro de una calle de la ciudad de una sola celda parece extremadamente ineficiente y es un elemento que debe intentarse mejorar en primer lugar.

Red avanzada para ciudad lineal
Y así, nos enfrentamos a la tarea de mejorar la Red Lineal para que no se convierta en una "cuadrada". La circunstancia que introduce la mayor ineficiencia en la operación de la Red Lineal es su unificación de todas las rutas en solo dos flujos de tráfico muy grandes. En esta situación, un paso razonable sería dividir los flujos a lo largo de sus dos carreteras en Q partes iguales. Dado que los costos de tiempo causados ​​por cada automóvil que se une o sale del tráfico son proporcionales a la intensidad del tráfico en él, como resultado de dividir las líneas de la calle en partes aisladas de Q (Fig. 41a), las pérdidas de cambio dentro de la ciudad lineal deberían haber disminuido en un factor de Q.


fig. 41

Simplemente construyendo diez caminos cercanos y esperando que los conductores mismos estén distribuidos equitativamente entre ellos; desafortunadamente, no parece tener nada que tenga posibilidades de éxito. Una decisión mucho más reflexiva es diseñar la red de manera que cada camino no conduzca a todos los barrios, sino solo a un pequeño "segmento" de la ciudad, donde sería difícil moverse por él (Fig. 41b).

Puede ver una idea similar en el esquema de movimiento de ascensores dentro de edificios de varios pisos. Allí, cada elevador le permite entrar y salir no en todos los pisos, sino solo dentro de un cierto rango de alturas. Tomando este concepto, echemos un vistazo más de cerca a la carretera r _k , que abre el acceso al segmento Δ _k = ( x _k ,x _{k +1} ] para viajes que comenzaron (no estrictamente) al sur de x _k (se cree que la numeración de los bloques se realiza de abajo hacia arriba). En el lado de cada trimestre, el número de los cuales (en sentido estricto) menos de x _{la k} , la carretera r _{la k} entra en el flujo q _en potencia | Δ _k | / n (1 / n cada dirección de cada cuarto dentro de Δ _k ), al mismo tiempo se supone que la capacidad de colapsar con r _khacia cualquiera de los trimestres mencionados falta debido a las normas de tránsito establecidas o por el diseño especial de la red de carreteras. Los automóviles

acumulados en el segmento [1, x _k ] eventualmente se distribuirán de manera uniforme entre los bloques de Δ _k , por lo tanto, si no hubo viajes cuyo comienzo y final se encuentran dentro de Δ _k , entonces el lado fluye q _{hacia afuera} en la dirección de cada uno de los bloques en esta sección tendría una potencia x _k / n (Fig. 42).


fig. 42

De hecho, la contribución de los viajes "internos" a la potencia de los flujos laterales también tiene lugar, sin embargo, el valor de esta contribución nunca excede | Δ _k | / n ; por lo tanto, en el caso cuando x _k >> | Δ _k |, puede ser simplemente descuidado. La potencia p _{k del} flujo principal a lo largo de r _k con las simplificaciones realizadas se representará mediante un gráfico de dos secciones rectas con un P _k máximo igual a x _k ⋅ | Δ _k | / n . El valor aproximado de las pérdidas de conmutación en r _k se puede encontrar mediante la fórmula:

I _k = ( α / 2 ν ) ⋅ ∑ _x [ q _in ( x ) ⋅ p _k ( x ) ⋅ (1 + 1 / s )] + ( α / 2 ν ) ⋅ ∑ _x [ q _out ( x ) ⋅ p _k ( x ) ⋅ (1 - 1 / s )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ∑ _x [| Δ _k | / n ⋅ p _k ( x )] + ( α / 2 ν ) ⋅ (1 - 1 / s ) ∑ _x [ x _k / n ⋅ p _k ( x )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / x _k + ( α / 2 ν ) ⋅ (1 - 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / | Δ _k |,

donde la primera suma se toma sobre el área x ∈ [1, x _k ], y la segunda sobre x ∈ Δ _k . Expresiones:

( ∑ _x p _k ( x )) / x _k , x ∈ [1, x _k ] y

( ∑ _x p _k ( x )) / | Δ _k |, x ∈ Δ _k

no hay nada más que la potencia promedio de la corriente a lo largo de r _k dentro de los intervalos indicados. Dado que el gráfico de potencia dentro de estos intervalos tiene la forma de una línea recta, la potencia promedio en ambos casos es P _k / 2. Sustitución
x _k ⋅ | Δ _k | / n en
P _k
finalmente damos la fórmula para la intensidad de pérdida a su forma más simple:

I _k = 2 ( α / 2 ν ) ⋅ P _k ⋅ P _k / 2 = ( α / 2 ν ) ⋅ P _k ²

Tratemos ahora de calcular la secuencia x _{k de los} números de esos trimestres por los cuales la ciudad lineal debe dividirse en segmentos. Como criterio para la selección de segmentos, tomamos el requisito de que la potencia máxima de los flujos de tráfico P _k en carreteras adecuadas tengan el mismo valor, independientemente de k , en otras palabras, la igualdad

x _k ⋅ | Δ _k | = Const.

Recordando eso | Δ _k | = x _{k + 1} - x _k , llegamos a la ecuación de diferencia:

x _{k + 1} - x _k = Const / x _k .

Suponiendo que x y k son variables continuas, y reemplazando

x _{k + 1} - x _k = x ( k + 1) - x ( k )

en d x / d k ⋅ 1,

podemos aproximar la ecuación de diferencia por diferencial:

d x / d k = Const / x <=> x d x = Const ⋅ d k .

De donde obtenemos para x _{k una} solución en la forma general:

x _k = C ₁ √ ( k + C ₂ ).

Nos queda por determinar el valor de las constantes C ₁ y C _{2 a} partir de las condiciones de contorno, sin embargo, hay una sutileza importante en este asunto. A diferencia de la situación en los segmentos restantes, todos los automóviles que llegaron desde la autopista occidental a los barrios del segmento número 1, dentro del mismo segmento, comenzaron su viaje. Como resultado, el gráfico de la potencia de flujo en la primera carretera hacia el norte tendrá la forma de una parábola invertida regular.

Al mismo tiempo, las condiciones a priori a partir de las cuales se obtuvo la fórmula para x _k esencialmente sugirieron que las gráficas de la potencia de los flujos en todas las carreteras deberían estar cerca de una vista triangular, y los viajes en sí mismos deberían comenzar principalmente fuera del segmento al que se dirigen. Estos requisitos se pueden cumplir con una precisión razonable si dividimos formalmente el primer segmento en dos partes iguales (la parábola es abordada por un triángulo isósceles y la mayoría de los viajes a lo largo de la primera carretera se dirigen desde la mitad sur del segmento número 1 a su mitad norte), sin aumentar el número de caminos ( fig 43).


fig. 43

Es el medio del primer segmento que debe considerarse el punto x ₁ en la fórmula para x _k . A partir de aquí obtenemos la primera condición límite:

x ₂ = 2 x ₁ o

√ (2 + C ₂ ) = 2 ⋅ √ (1 + C ₂ ) =>

C ₂ = - 2/3.

La segunda condición límite se obtiene del requisito de que las carreteras y los segmentos son exactamente Q , lo que significa que x _{Q + 1} debe ser igual al siguiente trimestre con el mayor número en la ciudad:

C ₁ √ ( Q + 1 - 2/3) = n + 1, de donde

C ₁ ≈ ( n + 1) / √ Q.

De esta manera:

x _k ≈ ( n + 1) ⋅ √ ( k - 2/3) / √ Q ,

El | Δ _k | ≈ d x / d k = ( n + 1) / 2√ ( k - 2/3) ⋅ √ Q

P _k = x _k ⋅ | Δ _k | / n =

= ( n + 1) 2/2 n ⋅ Q ≈ n / 2 Q

I _k = ( α / 2 ν ) ⋅ P _k ² =

= ( α / 2 ν ) ⋅ ( n / 2 Q ) ² .

Como todas las autopistas de la calle 2 Q generan pérdidas de la misma intensidad, el valor de los costos de cambio dentro de toda la red en su conjunto será:

I = 2 Q ⋅ ( α / 2 ν ) ⋅ ( n / 2 Q ) ² = ( α / 2 ν ) ⋅ n 2/2 Q.

Como puede ver, se logra lo deseado: después de dividir las carreteras principales en partes Q , las pérdidas realmente disminuyeron por un factor de Q (excepto por el coeficiente constante de 1/3 a 1/2 que aumentó en comparación con la fórmula para la ciudad lineal habitual). Bueno, la mitad del trabajo está hecho, queda por aplicar el resultado para mejorar la ciudad con la arquitectura celular.

Elevador de rascacielos en la ciudad celular
Para simplificar, nos contentaremos con un ejemplo de una ciudad en la que todas las calles son de sentido único. Usando la analogía entre Linear City y las calles individuales de Cellular City, dividimos la carretera a lo largo de esta última en partes Q. Por defecto, se cree que al salir del trimestre, puede acceder a cualquier carretera que pase cerca de él. Al mismo tiempo, entre todas las carreteras ubicadas a lo largo de una calle, hay un giro hacia un barrio específico con exactamente una de ellas. En el proceso de establecer reglas, su uniformidad y simplicidad son extremadamente importantes. Eche un vistazo a la Figura 44:


fig. 44

todas las calles tienen la misma apariencia y las mismas reglas, cuál de sus caminos en qué bloques de la cuenta abre el acceso. La Figura 45 muestra un diagrama de giros permitidos entre carreteras. Mirar esta imagen es difícil de no confundir. Lo mismo se dice a menudo sobre el esquema del metro en alguna gran ciudad. Sin embargo, en ambos casos, todo se vuelve claro y simple si conoce la lógica de la idea. La regla lógica de los giros permitidos parece bastante simple: si conduce a lo largo de una autopista, cruza las carreteras perpendicularmente a su movimiento y puede convertirse en un cuarto ubicado directamente detrás de ellas, puede girar en cualquiera de estas carreteras.


fig. 45

La topología de Skyscraper Lift es compatible con semáforos y pasos superiores. Es difícil, pero puede generalizarse a redes no necesariamente de estructura celular o lineal. Esto último es realmente importante para las ciudades históricas, donde es poco probable que sea correcto demoler la mitad de los monumentos históricos para colocar muchas calles pequeñas y rectas, pero en las que ya hay calles bastante grandes que pueden acomodar varias autopistas de dos o tres carriles.

Sobre los problemas del transporte y el trabajo de las matemáticas.

Es agradable completar el trabajo minucioso semestral. El trabajo que escribí, por supuesto, no resuelve todos los problemas y dificultades del diseño de carreteras: este negocio requiere una gran cantidad de personas muy diversas. Sin embargo, sus resultados brindan la oportunidad de ver errores importantes en ciudades ya construidas y proporcionan métodos para evitar dichos errores en el futuro. Este artículo no pretende ser un libro de referencia que cubra todos los casos posibles que un ingeniero puede encontrar en la práctica: consideré mi tarea principal dar un nuevo punto de vista, desarrollar una nueva forma de razonar y hablar sobre el problema, proporcionar el mínimo necesario de ejemplos de modelos simples preparados por el lector Ya podría expandirme.

Se vuelve triste cuando te das cuenta de cuánto tiempo perdieron los residentes de la ciudad en atascos debido al hecho de que en el momento adecuado no había matemático que pudiera pasar la noche en un problema completamente solucionable. ¿Cuántos de estos problemas aún rodean nuestra vida o se esconden en su profesión? ¿Está una persona sentada cerca de usted en el trabajo cuyas herramientas tienen un lápiz y una hoja de papel?

Espero que todo cambie para mejor.

¡Gracias por su atención y buena suerte!
Sergey Kovalenko.

Año 2019
magnolia@bk.ru


(Foto: Vincent Laforet)