Enfoque codicioso y máquinas tragamonedas. Análisis de las tareas de la ML-track del campeonato de programación.

Continuamos publicando análisis de las tareas que se propusieron en el reciente campeonato. A continuación se encuentran las tareas tomadas de la ronda de calificación para especialistas en aprendizaje automático. Esta es la tercera pista de cuatro (backend, frontend, ML, analytics). Los participantes debían hacer un modelo para corregir errores tipográficos en los textos, proponer una estrategia para jugar en máquinas tragamonedas, recordar un sistema de recomendaciones de contenido y componer varios programas más.

A. Typos

Condición

(epígrafe) (de un foro)
- ¿Quién compuso estas tonterías?
- Astrofísicos. Ellos también son personas.
- Cometiste 10 errores en la palabra "periodistas".

Muchos usuarios cometen errores de tipeo, algunos por presionar teclas y otros por analfabetismo. Queremos verificar si el usuario podría tener en mente otra palabra que no sea la que escribió.

Más formalmente, suponga que se produce el siguiente modelo de error: el usuario comienza con una palabra que quiere escribir y luego comete una serie de errores. Cada error es una sustitución de alguna subcadena de la palabra por otra subcadena. Un error corresponde a reemplazar solo en una posición (es decir, si el usuario quiere cometer un solo error por la regla "abc" → "cba", entonces de la cadena "abcabc" puede obtener "cbaabc" o "abccba"). Después de cada error, el proceso se repite. La misma regla podría usarse varias veces en diferentes pasos (por ejemplo, en el ejemplo anterior, "cbacba" podría obtenerse en dos pasos).

Es necesario determinar el número mínimo de errores que un usuario podría cometer si tuviera en mente una palabra determinada y escribiera otra.

Solución

Intentemos generar de la ortografía correcta todas las palabras posibles con no más de 4 errores. En el peor de los casos, puede haber O ((L﹒N) ⁴ ). En las limitaciones del problema, este es un número bastante grande, por lo que debe descubrir cómo reducir la complejidad. En su lugar, puede usar el algoritmo de encuentro en el medio: genere palabras con no más de 2 errores, así como palabras de las que puede obtener una palabra escrita por el usuario, cometiendo no más de 2 errores. Tenga en cuenta que el tamaño de cada uno de estos conjuntos no excederá de 10 ⁶ . Si el número de errores cometidos por el usuario no supera los 4, estos conjuntos se intersectarán. Del mismo modo, podemos verificar que el número de errores no exceda de 3, 2 y 1.

 struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; } 

B. Bandido de muchos brazos

Condición

Esta es una tarea interactiva.

Usted mismo no sabe cómo sucedió, pero se encontró en una sala con máquinas tragamonedas con una bolsa llena de fichas. Desafortunadamente, en la taquilla, se niegan a aceptar los tokens y decidiste probar suerte. Hay muchas máquinas tragamonedas en el pasillo que puedes jugar. Para un juego con una máquina tragamonedas, usa una ficha. En caso de ganar, la máquina le da un dólar, en caso de pérdida, nada. Cada máquina tiene una probabilidad fija de ganar (que no conoce), pero es diferente para diferentes máquinas. Después de estudiar el sitio web del fabricante de estas máquinas, descubrió que la probabilidad de ganar para cada máquina se selecciona aleatoriamente en la etapa de fabricación a partir de la distribución beta con ciertos parámetros.

Desea maximizar sus ganancias esperadas.

Solución

Este problema es bien conocido, podría resolverse de diferentes maneras. La decisión principal del jurado implementó la estrategia de muestreo de Thompson , pero dado que el número de pasos se conocía al comienzo del programa, existen estrategias más óptimas (por ejemplo, UCB1). Además, uno podría incluso pasar con la estrategia épsilon-codiciosa: con cierta probabilidad ε jugar una máquina aleatoria y con una probabilidad (1 - ε) jugar una máquina con las mejores estadísticas de victoria.

 class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self._bs = [init_b] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self.last_move = -1 random.seed(int(time.time())) def move(self): samples = [random.betavariate(self._as[x], self._bs[x]) for x in range(self.n)] self.last_move = max(range(self.n), key=lambda x: samples[x]) self.moves.append(self.last_move) return self.last_move def set_reward(self, reward): i = self.last_move r = reward self._as[i] += r self._bs[i] += (1 - r) return i, r while True: n, m = map(int, sys.stdin.readline().split()) if n == 0 and m == 0: break alpha, beta = map(float, sys.stdin.readline().split()) solver = ThompsonSampling(m) for _ in range(n): print >> sys.stdout, solver.move() + 1 sys.stdout.flush() reward = int(sys.stdin.readline()) solver.set_reward(reward) 

C. Alineación de oraciones

Condición

Una de las tareas más importantes para entrenar un buen modelo de traducción automática es un buen caso de oraciones paralelas. Por lo general, la fuente de ofertas paralelas son los documentos paralelos. Resulta que, a menudo, para construir un cierto corpus de oraciones paralelas, no necesita saber nada más que su longitud. En particular, puede notar que cuanto más larga sea la oración en el idioma de origen, más probablemente será traducida. Cierta dificultad radica en el hecho de que durante la traducción el número de oraciones en el texto puede cambiar: a veces dos oraciones adyacentes en la traducción se pueden combinar en una, o viceversa: una oración se puede dividir en dos. En algunos casos raros, las oraciones pueden omitirse por completo en una traducción, o una traducción puede aparecer en una traducción que no estaba en el original.

Más formalmente, suponga que el siguiente modelo generativo para recintos paralelos es verdadero. En cada paso, hacemos uno de los siguientes:

1. Parar

Con probabilidad p _h, finaliza _la generación de cascos.

2. [1-0] Saltar ofertas

Con probabilidad p _d, atribuimos una oración al texto original. No atribuimos nada a la traducción. La longitud de la oración en el idioma original L ≥ 1 se selecciona de la distribución discreta:

.

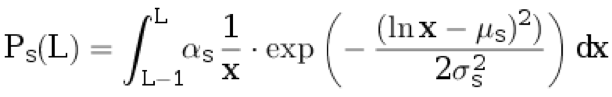
Aquí μ _s , σ _s son los parámetros de distribución, y α _s es el coeficiente de normalización elegido para que .

3. [0-1] Insertar propuesta

Con probabilidad p _i asignamos una oración a la traducción. No atribuimos nada al original. La longitud de una oración en un idioma de traducción L ≥ 1 se selecciona de una distribución discreta:

.

Aquí μ _t , σ _t son los parámetros de distribución, y α _t es el coeficiente de normalización elegido para que .

4. Traducción

Con probabilidad (1 - p _d - p _i - p _h ) tomamos la longitud de la oración en el idioma original L _s ≥ 1 de la distribución p _s (con redondeo). A continuación, generamos la longitud de la oración en el lenguaje de traducción L _t ≥ 1 a partir de la distribución discreta condicional:

.

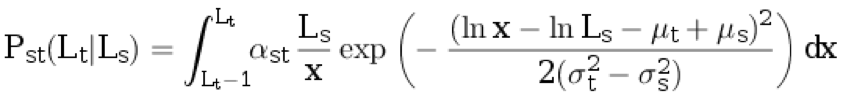
Aquí, α _st es el coeficiente de normalización, y los parámetros restantes se describen en los párrafos anteriores.

El siguiente es otro paso:

1. [2-1] Con probabilidad p _{dividida s, la} oración generada en el idioma original se divide en dos no vacías, de modo que el número total de palabras aumenta exactamente en una . La probabilidad de que una oración de longitud L _{s se} separe en partes de longitud L ₁ y L ₂ (es decir, L ₁ + L ₂ = L _s + 1) es proporcional a P _s (L ₁ ) ⋅ P _s (L ₂ ).

2. [1-2] Con la probabilidad p _{dividida t, la} oración generada en el idioma de destino se divide en dos oraciones no vacías, de modo que el número total de palabras aumenta exactamente en una. La probabilidad de que una oración de longitud L _{t se} separe en partes de longitud L1 y L2 (es decir, L ₁ + L ₂ = L _t + 1) es proporcional a P _t (L ₁ ) ⋅ P _t (L ₂ ).

3. 3. [1-1] Con una probabilidad de (1 - p _{dividido s} - p _{dividido t} ), ninguno de los par de oraciones generadas decaerá.

Solución

La tarea es un caso especial de alineación utilizando modelos ocultos de Markov (alineación HMM). La idea principal es que puede calcular la probabilidad de generar un par específico de documentos utilizando este modelo y el algoritmo de reenvío : en este caso, el estado es un par de prefijos de documentos. En consecuencia, la probabilidad requerida de alineación de un par específico de oraciones paralelas puede calcularse mediante el algoritmo de avance hacia atrás .

D. Cinta de recomendaciones

Condición

Considere una fuente de recomendaciones para contenido heterogéneo. Mezcla objetos de varios tipos (imágenes, videos, noticias, etc.). Estos objetos generalmente están ordenados por relevancia para el usuario: cuanto más relevante (interesante) sea el objeto para el usuario, más cerca estará al principio de la lista de recomendaciones. Sin embargo, con este orden, a menudo surgen situaciones en las que varios objetos del mismo tipo aparecen en la lista de recomendaciones. Esto empeora en gran medida la variedad externa de nuestras recomendaciones y, por lo tanto, a los usuarios no les gusta. Es necesario implementar un algoritmo que, de acuerdo con la lista de recomendaciones, constituirá una nueva lista que estará libre de este problema y será más relevante.

Sea una lista inicial de recomendaciones a = [a ₀ , a ₁ , ..., a _{n - 1} ] de longitud n> 0. Un objeto con número i tiene tipo con número b _i b {0, ..., m - 1}. Además, un objeto bajo el número i tiene relevancia r (a _i ) = 2 _−i . Considere la lista que se obtiene de la inicial eligiendo un subconjunto de objetos y su permutación: x = [a _{i 0} , a _{i 1} , ..., a _{i k - 1} ] de longitud k (0 ≤ k ≤ n). Una lista se llama admisible si no coinciden dos objetos consecutivos en ella, es decir, b _{i j} ≠ b _{i j + 1} para todo j = 0, ..., k - 2. La relevancia de la lista se calcula mediante la fórmula. $$$\ sum_ {j = 0} ^ {k-1} 2 _ {- j} r (a_ {i_j})$. Necesita encontrar la lista de relevancia máxima entre todas las válidas.

Solución

Utilizando cálculos matemáticos simples, se puede demostrar que el problema se puede resolver mediante un enfoque "codicioso", es decir, en la lista óptima de recomendaciones, cada elemento tiene el objeto más relevante de todos los que son válidos al mismo comienzo de la lista. La implementación de este enfoque es simple: tomamos objetos en una fila y los agregamos a la respuesta, si es posible. Cuando se encuentra un objeto no válido (cuyo tipo coincide con el tipo del anterior), lo ponemos a un lado en una cola separada, desde la cual lo insertamos en la respuesta lo antes posible. Tenga en cuenta que en todo momento, todos los objetos en esta cola tendrán un tipo coincidente. Al final, varios objetos pueden permanecer en la cola, ya no se incluirán en la respuesta.

  std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; } 

D. Clusterización de secuencias de caracteres.

Hay un alfabeto finito A = {a ₁ , a ₂ , ..., a _{K - 1} , a _K = S}, a _i ∈ {a, b, ..., z}, S es el final de la línea.

Considere el siguiente método para generar cadenas aleatorias sobre el alfabeto A:

1. El primer carácter x ₁ es una variable aleatoria con la distribución P (x ₁ = a _i ) = q _i (se sabe que q _K = 0).
2. Cada siguiente carácter se genera en base al anterior de acuerdo con la distribución condicional P (x _i = a _j || x _{i - 1} = a _l ) = p _jl .
3. Si x _i = S, la generación se detiene y el resultado es x ₁ x ₂ ... x _{i - 1} .

Se da el conjunto de líneas generadas a partir de una mezcla de dos modelos descritos con diferentes parámetros. Es necesario que cada fila proporcione el índice de la cadena a partir de la cual se generó.

Solución

El problema se resuelve utilizando el algoritmo EM : se supone que la muestra presentada se genera a partir de una mezcla de dos cadenas de Markov cuyos parámetros se restauran durante las iteraciones. Se realiza una restricción del 80% de las respuestas correctas para que la corrección de la solución no se vea afectada por ejemplos que tienen una alta probabilidad en ambas cadenas. Por lo tanto, estos ejemplos, cuando se restauran correctamente, se pueden asignar a una cadena que es incorrecta en términos de la respuesta generada.

 import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs] # probs fixed p0, A = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) q0, B = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) for prob, sample in zip(probs, samples): p0[sample[0]] += prob q0[sample[0]] += 1 - prob for t1, t2 in zip(sample[:-1], sample[1:]): A[t1][t2] += prob B[t1][t2] += 1 - prob A, p0 = normalized_matrix(A), normalized_row(p0) B, q0 = normalized_matrix(B), normalized_row(q0) trans_log_diff = [ [math.log(b + EPS) - math.log(a + EPS) for b, a in zip(B_r, A_r)] for B_r, A_r in zip(B, A) ] # A, p0, B, q0 fixed probs = empty_row(n_samples) for i, sample in enumerate(samples): value = math.log(q0[sample[0]] + EPS) - math.log(p0[sample[0]] + EPS) for t1, t2 in zip(sample[:-1], sample[1:]): value += trans_log_diff[t1][t2] probs[i] = 1.0 / (1.0 + math.exp(value)) if max(abs(x - y) for x, y in zip(probs, old_probs)) < 1e-9: break return [int(x > 0.5) for x in probs] def main(): N, K = list(map(int, input().split())) string_samples = [] alphabet = list(input().strip()) + [''] for _ in range(N): string_samples.append(input().rstrip()) result = restore_params(alphabet, string_samples) for r in result: print(r) if __name__ == '__main__': main() 

---

.