El algoritmo de colapso de la función de onda enseña a una computadora a improvisar. En la entrada, recibe datos arquetípicos y crea datos generados por procedimientos similares al original.
( Fuente )La mayoría de las veces se usa para crear imágenes, pero también puede construir
ciudades ,
parques de skate y escribir
poemas terribles .
( Fuente )El colapso de la función de onda es un algoritmo de mente muy independiente que prácticamente no requiere ayuda o instrucciones del exterior. Solo necesita un ejemplo del estilo que desea lograr, y él hará el resto. A pesar de su autosuficiencia, es sorprendentemente simple. No utiliza redes neuronales, bosques aleatorios ni ninguna otra cosa que se parezca al aprendizaje automático. Si manejas la idea, será muy comprensible e intuitiva para ti.
La mayoría de las implementaciones y explicaciones del colapso de la función de onda son una versión completa y de velocidad optimizada del algoritmo. Por supuesto, todos ellos son importantes y necesarios, pero es difícil entenderlos desde cero. En esta publicación, explicaré todo en un lenguaje simple que entiendo, centrándome en la versión limitada de Wavefunction, que llamé
Modelo de mosaico
aún más simple . Además,
publiqué un ejemplo de implementación de ESTM en Github . El código que contiene es ineficiente y lento, pero muy legible y comentado en detalle. Tan pronto como comprenda la tecnología subyacente de ESTM, estará más cerca de comprender versiones más complejas del algoritmo. Si desea comprender el algoritmo de colapso de la función de onda, este artículo será un buen comienzo.
Comencemos con la historia.
La boda
Imagina que estás planeando tu boda. Además de la selección de joyas y música, debe crear un plan de asientos para los invitados a cenar. A su familia le gusta discutir y ser travieso, por lo que puede ser difícil. Un padre no puede sentarse a menos de dos mesas de su madre. Una prima se siente sola si no se sienta con otra prima. Y es mejor no plantar al tío Roy junto a miembros de la familia de su pareja que no dañan el medio ambiente. Quedan solo 5 horas antes de la llegada de los alimentos, por lo que decide atacar esta obstinada tarea utilizando el algoritmo de colapso de la función de onda.
Comienza con una larga lista de reglas y un plan de asientos vacío.
Crea la
función de onda original
del plan. Ella ata cada silla a una lista de personas que pueden sentarse en ella. Mientras que cualquier persona puede sentarse en cualquier silla. La función de onda de los invitados sentados comienza con una
superposición completa (el concepto está tomado de la física cuántica) de cada posible esquema.
El gato de Schrödinger estaba vivo y muerto al mismo tiempo hasta que alguien abrió la caja y marcó; su plan es al mismo tiempo todos los esquemas posibles hasta que ponga las cosas en orden. Una superposición completa es una construcción teórica útil, pero no ayudará a su abuela a descubrir dónde necesita sentarse. Debe llevar la función de onda de la ubicación de los invitados a un solo estado determinado, que luego se puede convertir en tarjetas de presentación normales y no cuánticas.
Comenzamos a hacer esto realizando el
colapso de la función de onda para una silla. Seleccionamos una silla, miramos la lista de personas que pueden sentarse en ella y la asignamos aleatoriamente a una de ellas. En este caso, la función de onda de las heces se colapsa.
Esta elección tiene consecuencias que se extienden a las funciones de onda de las sillas restantes. Si el tío Roy está sentado en la mesa 2, entonces el primo Frank y Michelle Obama (un amigo de la familia de su pareja) definitivamente no estarán con él. Y si Michelle no se sienta en la mesa 2, Barack tampoco estará detrás de él. Estamos actualizando la función de onda del plan de ubicación eliminando personas de las listas de posibles candidatos.
Tan pronto como se resuelven las vibraciones, repetimos este proceso. Seleccionamos otra silla con varios posibles candidatos y colapsamos su función de onda, eligiendo aleatoriamente a una de las personas aceptables para ella. Nuevamente, extendemos las vibraciones causadas por esta elección al resto del plan, eliminando a las personas de la función de onda de la silla si ya no pueden sentarse en ella.
Repetimos este proceso ya sea hasta que la función de onda colapse (es decir, exactamente 1 persona sentada permanece en él), o hasta que lleguemos a una
contradicción . La contradicción es una silla en la que nadie puede sentarse, porque todos fueron expulsados debido a elecciones anteriores. La contradicción hace que la imposibilidad del colapso de toda la onda funcione.
Si ha llegado a una contradicción, entonces la forma más fácil es comenzar de nuevo. Deseche todo el trabajo anterior, encuentre un nuevo plan vacío e inicie el algoritmo nuevamente, completando el colapso de la función de onda para otra silla aleatoria. También puede implementar un sistema de retroceso que le permita cancelar una elección en particular, en lugar de abandonar inmediatamente todo ("¿y si Sheila es transferida a la silla 54?").
Después de algunos comienzos falsos, finalmente alcanzará un estado completamente colapsado en el que cada silla se asigna exactamente a una persona y se siguen todas las reglas. Hecho
De la boda a los mapas de bits
Este no es un ejemplo teórico. Realmente puede darse cuenta de una variante del colapso de la función de onda, que creará un plan de asientos para los invitados a la boda. Sin embargo, en el colapso de la función de onda más tradicional, generalmente tratamos de no sentar a las personas en la boda, sino de organizar los píxeles en la imagen de salida. Sin embargo, el proceso será muy similar. Enseñamos al algoritmo un conjunto de reglas que la salida debe satisfacer. Inicializamos la función de onda. Realizamos el colapso de un elemento y extendemos las consecuencias al resto de la función de onda. Y continuamos haciéndolo, ya sea hasta que la función de onda colapse completamente, o hasta que lleguemos a una contradicción.
El colapso tradicional de la función de onda difiere del colapso de la boda en la forma en que enseñamos al algoritmo las reglas que debe seguir. En la versión de la boda, tuvimos que escribir las reglas nosotros mismos. Pero en la versión tradicional, solo le damos al algoritmo una imagen de ejemplo, y en base a ello, el algoritmo crea el resto. Analiza un ejemplo, analiza sus patrones y descubre cómo deben alinearse los píxeles o los
mosaicos .
Comencemos a investigar el colapso real de una función de onda observando un caso especial simple, que
ExUtumno (el creador del algoritmo) llama el
Modelo de ExUtumno simple .
Modelo de mosaico simple
En el modelo en mosaico simple, las imágenes de entrada y salida se construyen a partir de un pequeño número de mosaicos predefinidos, y cada cuadrado en la imagen de salida se limita solo a sus cuatro vecinos más cercanos. Por ejemplo, supongamos que generamos mundos aleatorios para un juego bidimensional con una vista superior. Podemos tener baldosas para tierra, costa y mar, así como un conjunto de reglas como "la costa puede estar cerca del mar", "la tierra puede estar cerca de la costa" y "el mar puede estar al lado de otro mar".
El modelo de mosaico simple tiene en cuenta la simetría y la rotación de sus mosaicos. Por ejemplo, la tierra puede estar cerca de la costa, pero solo en la orientación correcta.
Este procesamiento de simetría proporciona mejores imágenes de salida, pero complica el código. Para simplificar las cosas, echemos un vistazo a una vista aún más simple del colapso de la función de onda, que llamé
Modelo de mosaico aún más simple .
Modelo de mosaico aún más simple
Incluso el modelo de mosaico más simple ("un modelo de mosaico aún más simple") es similar al modelo de mosaico simple, pero sus mosaicos no tienen propiedades de simetría. Cada mosaico es un píxel del mismo color, es decir, no podremos confundir sus bordes de ninguna manera.
Incluso las reglas de modelo de mosaico más simple determinan qué mosaicos se pueden colocar uno al lado del otro y en qué orientación. Cada regla es una tupla de tres elementos (3 tuplas): dos fichas y una dirección. Por ejemplo,
(SEA, COAST, LEFT) significa que el mosaico de
SEA (mar) puede
desde el mosaico de
COAST (costa). Esta regla debe ir acompañada de otra regla que describa la situación en términos de
COAST -
(COAST, SEA, RIGHT) .
Si desea que las fichas
SEA ubiquen no solo a la
, sino también a la
desde las fichas
COAST . entonces necesitan reglas adicionales:
(SEA, COAST, RIGHT) y
(COAST, SEA, LEFT) .
Como dije anteriormente, no necesitamos crear una lista de todas estas reglas nosotros mismos. El colapso de la función de onda puede crear un conjunto de reglas para un modelo de mosaico aún más simple al analizar una imagen de ejemplo y recopilar una lista de las 3 tuplas que contiene.
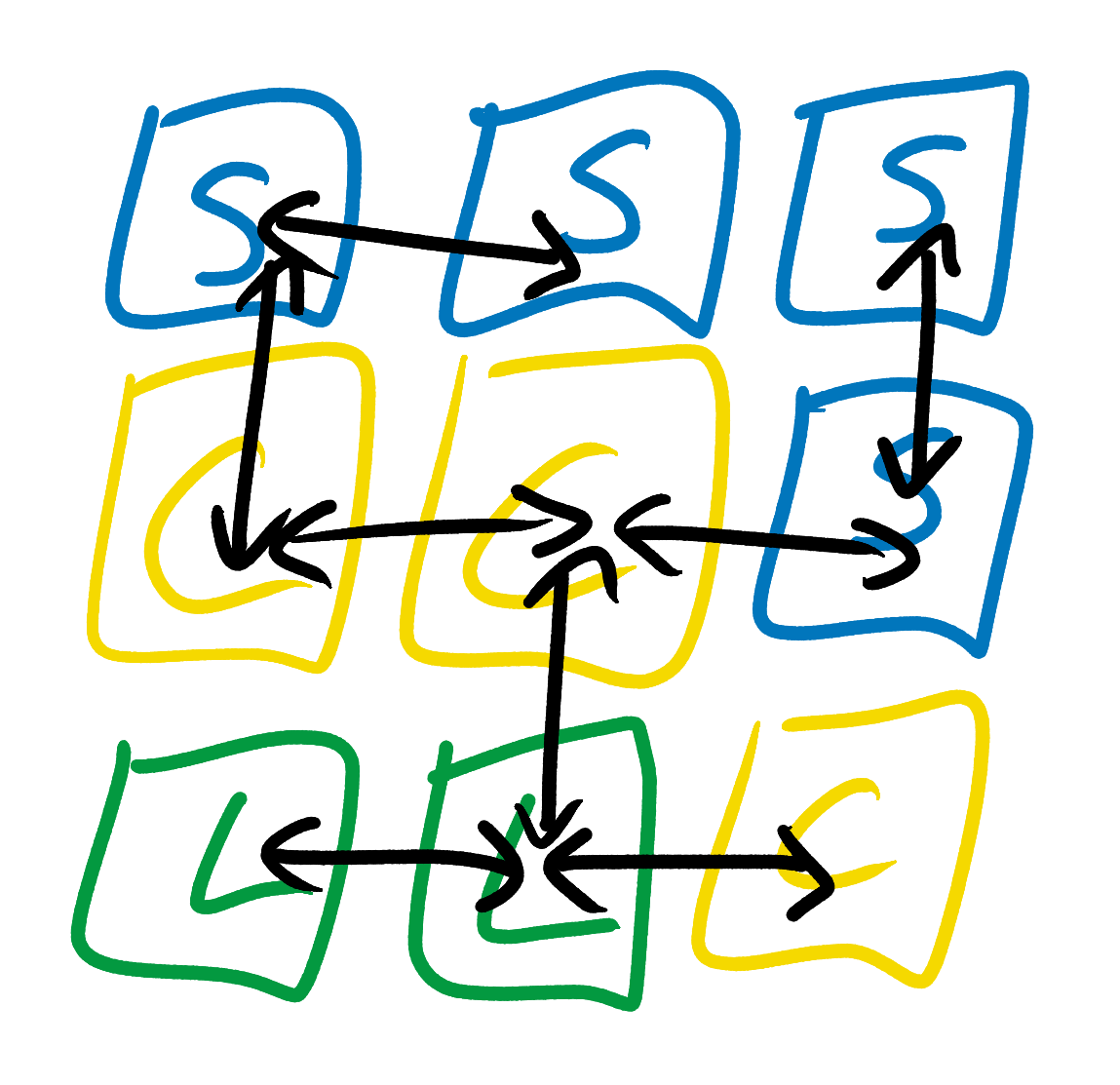
Después de examinar la imagen de ejemplo que se muestra arriba, Even Simpler Tiled Model nota que las baldosas marinas solo pueden estar debajo o al costado de las baldosas costeras, o en cualquier lugar cerca de otras baldosas marinas. También señala que las baldosas costeras pueden ubicarse junto a la tierra, el mar u otras baldosas costeras, pero solo por encima de las baldosas marinas y debajo de las baldosas terrestres. Ella no intenta derivar reglas más complejas, por ejemplo, "las baldosas marinas deben estar cerca de al menos una baldosa marina" o "cada isla debe contener al menos una baldosa terrestre". Ninguno de los mosaicos puede afectar el hecho de que algunos tipos de mosaicos pueden o no ubicarse a dos o más cuadrados de ellos. Esto es similar a un modelo de plan de boda en el que la única regla es: "X puede sentarse al lado de Y".
Al analizar la imagen entrante, también debemos registrar la frecuencia con la que se encuentra cada uno de los mosaicos. Más tarde, usamos estos números como pesos al elegir la función de onda del cuadrado, cuyo colapso debe realizarse, y también al elegir el mosaico asignado al cuadrado cuando se contrae.
Habiendo aprendido las reglas que debe cumplir la imagen de salida, estamos listos para construir el colapso de la función de onda de la imagen de salida.
Colapso
Como en el ejemplo de la boda, comenzamos el proceso de colapso con una función de onda en la que cada cuadrado de la imagen de salida está en una superposición de cada tipo de mosaico.
Comenzamos eligiendo un cuadrado cuya función de onda colapsará. En el ejemplo de la boda, esta elección se hizo por casualidad. Sin embargo, como señaló
ExUtumno , las personas generalmente abordan estas tareas de manera diferente. En cambio, buscan cuadrados con la
entropía más baja. La entropía es una medida de incertidumbre y desorden. En general, un cuadrado con alta entropía es un cuadrado con muchos mosaicos posibles restantes en su función de onda. Todavía no está claro a qué azulejo finalmente se derrumba. Un cuadrado de baja entropía es un cuadrado con la menor cantidad posible de mosaicos en la función de onda. El conjunto de fichas, a una de las cuales se derrumba como resultado, ya es muy limitado.
Por ejemplo, en el modelo de mosaico aún más simple, un cuadrado sin información sobre los cuadrados circundantes es ilimitado y puede convertirse en cualquier mosaico. Por lo tanto, tiene una entropía muy alta. Pero un cuadrado alrededor del cual varios cuadrados ya se han derrumbado puede tener la opción de solo 2 fichas.
La función de onda del cuadrado central en la figura anterior no colapsó por completo, pero ya sabemos que no puede ser una baldosa. Sin embargo, ya es limitado, lo que significa que tiene una
entropía más baja que la del cuadrado superior derecho, que aún puede ser terrestre, marítimo o costero.
Se trata de mosaicos tan limitados con baja entropía que las personas suelen prestar atención cuando resuelven manualmente dichos problemas. Incluso si no utiliza el colapso de la función de onda para crear un plan para colocar invitados en la boda y lo elaborará por su cuenta, aún se centrará en aquellas áreas del plan que ya tienen el mayor número de restricciones. No pondrás a Dwayne en la mesa 1, y luego saltarás al azar para llevar a Katie a la mesa 7 (que está vacía hasta ahora). Primero pones a Dwayne, luego descubrirás quién puede sentarse junto a él, luego quién puede sentarse al lado de esta persona, y así sucesivamente. Todavía no he visto la razón de esto, pero mi intuición dice que el uso de esta
heurística de entropía mínima es probable que genere menos
contradicciones que cuando se eligen al azar los cuadrados para el colapso.
La
fórmula de Shannon se usa como fórmula de entropía en el algoritmo de colapso de la función de onda. Utiliza los pesos de los mosaicos que analizamos de la imagen entrante en el paso anterior:
# Sums are over the weights of each remaining # allowed tile type for the square whose # entropy we are calculating. shannon_entropy_for_square = log(sum(weight)) - (sum(weight * log(weight)) / sum(weight))
Habiendo calculado el cuadrado de la función de onda con la entropía más pequeña, colapsamos su función de onda. Hacemos esto eligiendo aleatoriamente uno de los mosaicos que todavía están disponibles para el cuadrado, ponderado por el peso de los mosaicos que analizamos a partir de la imagen entrante. Se utilizan pesos porque proporciona una imagen de salida más realista. Suponga que la función de onda de un cuadrado informa que puede ser terrestre o costera. No siempre tenemos que elegir una de las opciones con una probabilidad del 50%. Si la imagen de entrada tiene más mosaicos de tierra que la costa, entonces deberíamos reflejar esta ventaja en la imagen de salida. Esto se realiza utilizando pesos globales simples. Si en la imagen de ejemplo hay
20 fichas de tierra y
10 fichas de costa, entonces el cuadrado colapsa en tierra con una probabilidad de
2/3 , y en la costa, con la probabilidad restante de
1/3 .
Luego extendemos las consecuencias de la elección al resto de la función de onda de la salida ("si ese mosaico resultó ser el mar, entonces este mosaico no puede ser tierra, es decir, no puede ser la costa"). Cuando todos estos temblores se hayan calmado, repetimos el proceso utilizando la heurística de entropía mínima para seleccionar el siguiente mosaico de colapso. Repetimos este ciclo de colapso-propagación, ya sea hasta que la función de onda completa de la imagen de salida colapse completamente y podamos devolver el resultado, o hasta que lleguemos a una contradicción y regresemos un error.
Como resultado, creamos un mundo (o error).
A donde ir ahora
Habiendo tratado con el modelo de mosaico aún más simple, está listo para ascender en la escala de poder y complejidad del algoritmo. Comience con el Modelo de mosaico simple que mencionamos al principio de esta publicación, luego continúe con el Modelo de superposición completo. En el modelo superpuesto, los mosaicos o píxeles se afectan entre sí desde la distancia. Si comprende tales cosas,
ExUtumno da cuenta de que el Modelo en
ExUtumno simple es similar a la cadena de Markov de orden 1, y los modelos más complejos se asemejan a cadenas de un orden mayor.
El colapso de la función de onda puede incluso tener en cuenta restricciones adicionales, por ejemplo, "este mosaico debe ser marino" o "este píxel debe ser rojo" o "solo puede haber un monstruo en la salida". Todo esto se describe en el
archivo README del proyecto principal . También puede estudiar las optimizaciones de velocidad realizadas para la implementación completa. No es necesario volver a calcular la entropía de cada cuadrado en cada iteración, y la difusión de información por la función de onda se puede hacer mucho más rápido. Estos aspectos se vuelven más importantes a medida que aumenta el tamaño de las imágenes de salida.
El colapso de la función de onda es una herramienta hermosa y poderosa que vale la pena dominar. Piénselo la próxima vez que planee una boda o genere un mundo procesal.