Redes neuronales y aprendizaje profundo, Capítulo 4: Prueba visual de que las redes neuronales pueden calcular cualquier función

En este capítulo, doy una explicación simple y principalmente visual del teorema de universalidad. Para seguir el material de este capítulo, no tiene que leer los anteriores. Está estructurado como un ensayo independiente. Si tiene la comprensión más básica de NS, debería poder entender las explicaciones.


Uno de los hechos más sorprendentes sobre las redes neuronales es que pueden calcular cualquier función. Es decir, digamos que alguien le da algún tipo de función compleja y sinuosa f (x):



E independientemente de esta función, se garantiza una red neuronal tal que para cualquier entrada x, el valor f (x) (o alguna aproximación cercana a él) será la salida de esta red, es decir:



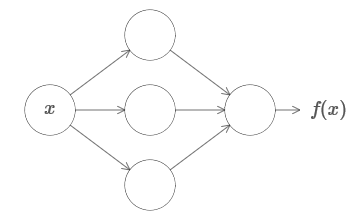
Esto funciona incluso si es una función de muchas variables f = f (x ₁ , ..., x _m ), y con muchos valores. Por ejemplo, aquí hay una red que calcula una función con m = 3 entradas yn = 2 salidas:



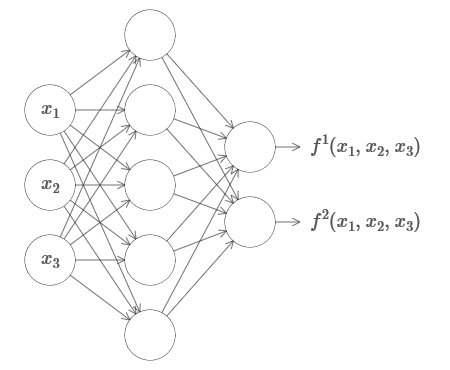
Este resultado sugiere que las redes neuronales tienen una cierta universalidad. No importa qué función queramos calcular, sabemos que hay una red neuronal que puede hacer esto.

Además, el teorema de universalidad se mantiene incluso si restringimos la red a una sola capa entre las neuronas entrantes y salientes, la llamada en una capa oculta Entonces, incluso las redes con una arquitectura muy simple pueden ser extremadamente poderosas.

El teorema de universalidad es bien conocido por las personas que usan redes neuronales. Pero aunque esto es así, la comprensión de este hecho no está tan extendida. Y la mayoría de las explicaciones para esto son demasiado complejas técnicamente. Por ejemplo, uno de los primeros documentos que prueban este resultado utiliza el teorema de Hahn - Banach , el teorema de representación de Riesz y algunos análisis de Fourier. Si usted es matemático, es fácil para usted comprender esta evidencia, pero para la mayoría de las personas no es tan fácil. Es una pena, porque las razones básicas para la universalidad son simples y hermosas.

En este capítulo, doy una explicación simple y principalmente visual del teorema de universalidad. Iremos paso a paso a través de las ideas subyacentes. Comprenderá por qué las redes neuronales realmente pueden calcular cualquier función. Comprenderá algunas de las limitaciones de este resultado. Y comprenderá cómo se asocia el resultado con NS profunda.

Para seguir el material de este capítulo, no tiene que leer los anteriores. Está estructurado como un ensayo independiente. Si tiene la comprensión más básica de NS, debería poder entender las explicaciones. Pero a veces proporcionaré enlaces a material anterior para ayudar a llenar los vacíos de conocimiento.

Los teoremas de universalidad a menudo se encuentran en la informática, por lo que a veces incluso olvidamos lo increíbles que son. Pero vale la pena recordarse: la capacidad de calcular cualquier función arbitraria es realmente sorprendente. Casi cualquier proceso que pueda imaginar puede reducirse al cálculo de una función. Considere la tarea de encontrar el nombre de una composición musical basada en un breve pasaje. Esto puede considerarse un cálculo de función. O considere la tarea de traducir un texto chino al inglés. Y esto puede considerarse un cálculo de función (de hecho, muchas funciones, ya que hay muchas opciones aceptables para traducir un solo texto). O considere la tarea de generar una descripción de la trama de la película y la calidad de la actuación basada en el archivo mp4. Esto también puede considerarse como el cálculo de una determinada función (la observación hecha sobre las opciones de traducción de texto también es correcta aquí). La universalidad significa que, en principio, los NS pueden realizar todas estas tareas y muchas otras.

Por supuesto, solo por el hecho de que sabemos que hay NS capaces de, por ejemplo, traducir del chino al inglés, no se deduce que tengamos buenas técnicas para crear o incluso reconocer dicha red. Esta restricción también se aplica a los teoremas de universalidad tradicionales para modelos como los esquemas booleanos. Pero, como ya hemos visto en este libro, el NS tiene algoritmos poderosos para las funciones de aprendizaje. La combinación de algoritmos de aprendizaje y versatilidad es una combinación atractiva. Hasta ahora, en el libro, nos hemos concentrado en algoritmos de entrenamiento. En este capítulo, nos centraremos en la versatilidad y lo que significa.

Dos trucos

Antes de explicar por qué el teorema de universalidad es verdadero, quiero mencionar dos trucos contenidos en la declaración informal "una red neuronal puede calcular cualquier función".

En primer lugar, esto no significa que la red pueda usarse para calcular con precisión cualquier función. Solo podemos obtener una aproximación tan buena como la que necesitamos. Al aumentar el número de neuronas ocultas, mejoramos la aproximación. Por ejemplo, anteriormente ilustré una red que computa una determinada función f (x) usando tres neuronas ocultas. Para la mayoría de las funciones, usando tres neuronas, solo se puede obtener una aproximación de baja calidad. Al aumentar el número de neuronas ocultas (por ejemplo, hasta cinco), generalmente podemos obtener una aproximación mejorada:



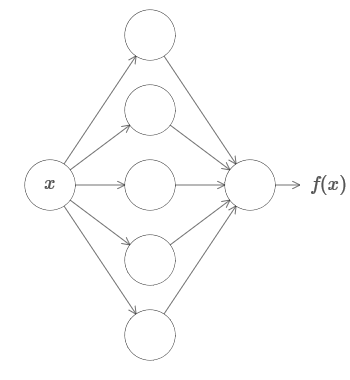
Y para mejorar la situación aumentando aún más el número de neuronas ocultas.

Para aclarar esta afirmación, digamos que se nos dio una función f (x), que queremos calcular con cierta precisión necesaria ε> 0. Hay una garantía de que cuando se usa un número suficiente de neuronas ocultas, siempre podemos encontrar un NS cuya salida g (x) satisfaga la ecuación | g (x) −f (x) | <ε para cualquier x. En otras palabras, la aproximación se logrará con la precisión deseada para cualquier posible valor de entrada.

El segundo problema es que las funciones que pueden ser aproximadas por el método descrito pertenecen a una clase continua. Si la función se interrumpe, es decir, realiza saltos bruscos repentinos, entonces, en el caso general, será imposible aproximarse con la ayuda de NS. Y esto no es sorprendente, ya que nuestros NS calculan funciones continuas de datos de entrada. Sin embargo, incluso si la función que realmente necesitamos calcular es discontinua, la aproximación es a menudo bastante continua. Si es así, entonces podemos usar NS. En la práctica, esta limitación generalmente no es importante.

Como resultado, una declaración más precisa del teorema de universalidad será que NS con una capa oculta puede usarse para aproximar cualquier función continua con la precisión deseada. En este capítulo, demostramos una versión un poco menos rigurosa de este teorema, utilizando dos capas ocultas en lugar de una. En las tareas, describiré brevemente cómo se puede adaptar esta explicación, con cambios menores, a una prueba que use solo una capa oculta.

Versatilidad con un valor de entrada y uno de salida.

Para entender por qué el teorema de universalidad es verdadero, comenzamos por comprender cómo crear una función de aproximación NS con solo un valor de entrada y un valor de salida:



Resulta que esta es la esencia de la tarea de la universalidad. Una vez que comprendamos este caso especial, será bastante fácil extenderlo a funciones con muchos valores de entrada y salida.

Para comprender cómo construir una red para contar f, comenzamos con una red que contiene una sola capa oculta con dos neuronas ocultas, y con una capa de salida que contiene una neurona de salida:



Para imaginar cómo funcionan los componentes de la red, nos enfocamos en la neurona oculta superior. En el diagrama del artículo original, puede cambiar interactivamente el peso con el mouse haciendo clic en "w" e inmediatamente ver cómo cambia la función calculada por la neurona oculta superior:



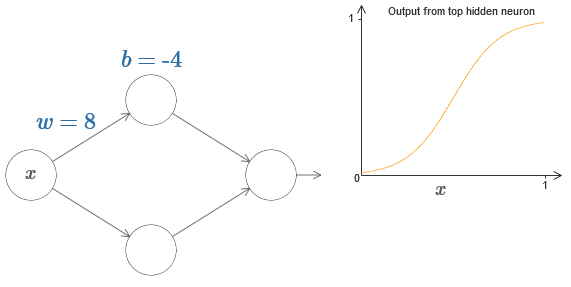
Como aprendimos anteriormente en el libro, una neurona oculta cuenta σ (wx + b), donde σ (z) ≡ 1 / (1 + e ^−z ) es un sigmoide . Hasta ahora, hemos usado esta forma algebraica con bastante frecuencia. Sin embargo, para probar la universalidad sería mejor si ignoramos por completo este álgebra y, en su lugar, manipulamos y observamos la forma en el gráfico. Esto no solo lo ayudará a sentir mejor lo que está sucediendo, sino que también nos dará una prueba de universalidad aplicable a otras funciones de activación además de sigmoide.

Estrictamente hablando, el enfoque visual que he elegido tradicionalmente no se considera evidencia. Pero creo que el enfoque visual proporciona más información sobre la verdad del resultado final que la prueba tradicional. Y, por supuesto, tal comprensión es el verdadero propósito de la prueba. En la evidencia que propongo, las brechas ocasionalmente se encontrarán; Daré evidencia visual razonable, pero no siempre rigurosa. Si esto te molesta, entonces considera que es tu tarea llenar estos vacíos. Sin embargo, no pierda de vista el objetivo principal: comprender por qué el teorema de universalidad es verdadero.

Para comenzar con esta prueba, haga clic en el desplazamiento b en el diagrama original y arrastre hacia la derecha para agrandarlo. Verá que con un aumento en el desplazamiento, el gráfico se mueve hacia la izquierda, pero no cambia de forma.

Luego arrástrelo hacia la izquierda para reducir el desplazamiento. Verá que el gráfico se mueve hacia la derecha sin cambiar de forma.

Reduce el peso a 2-3. Verá que a medida que disminuye el peso, la curva se endereza. Para que la curva no se salga del gráfico, es posible que deba corregir el desplazamiento.

Finalmente, aumente el peso a valores superiores a 100. La curva se hará más empinada y eventualmente se acercará al paso. Intente ajustar el desplazamiento para que su ángulo esté en la región del punto x = 0.3. El siguiente video muestra lo que debería suceder:



Podemos simplificar en gran medida nuestro análisis aumentando el peso para que la salida sea realmente una buena aproximación de la función de paso. A continuación construí la salida de la neurona oculta superior para el peso w = 999. Esta es una imagen estática:



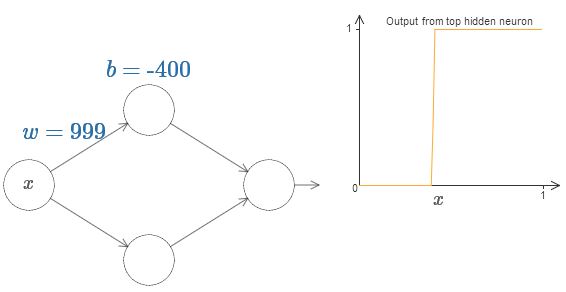
Usar funciones escalonadas es un poco más fácil que con un sigmoide típico. La razón es que las contribuciones de todas las neuronas ocultas se suman en la capa de salida. La suma de un montón de funciones de pasos es fácil de analizar, pero es más difícil hablar sobre lo que sucede cuando se agregan un montón de curvas en forma de sigmoide. Por lo tanto, será mucho más simple suponer que nuestras neuronas ocultas producen funciones escalonadas. Más precisamente, hacemos esto fijando el peso w en un valor muy grande y luego asignando la posición del paso a través del desplazamiento. Por supuesto, trabajar con una salida como una función de paso es una aproximación, pero es muy bueno, y hasta ahora trataremos la función como una verdadera función de paso. Más tarde, volveré a discutir el efecto de las desviaciones de esta aproximación.

¿Qué valor de x es el paso? En otras palabras, ¿cómo depende la posición del escalón del peso y el desplazamiento?

Para responder la pregunta, intente cambiar el peso y el desplazamiento en el gráfico interactivo. ¿Puedes entender cómo la posición del paso depende de w y b? Al practicar un poco, puedes convencerte de que su posición es proporcional a b e inversamente proporcional a w.

De hecho, el paso está en s = −b / w, como se verá si ajustamos el peso y el desplazamiento a los siguientes valores:



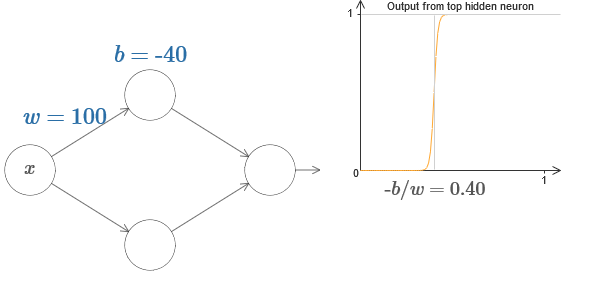
Nuestras vidas se simplificarán enormemente si describimos las neuronas ocultas con un solo parámetro, s, es decir, por la posición del paso, s = −b / w. En el siguiente diagrama interactivo, simplemente puede cambiar s:



Como se señaló anteriormente, asignamos especialmente un peso w en la entrada a un valor muy grande, lo suficientemente grande como para que la función de paso se convierta en una buena aproximación. Y podemos volver fácilmente la neurona parametrizada de esta manera a su forma habitual eligiendo el sesgo b = −ws.

Hasta ahora, nos hemos concentrado en la salida de solo la neurona oculta superior. Veamos el comportamiento de toda la red. Suponga que las neuronas ocultas calculan las funciones de paso definidas por los parámetros de los pasos s ₁ (neurona superior) y s ₂ (neurona inferior). Sus respectivos pesos de salida son w ₁ yw ₂ . Aquí está nuestra red:



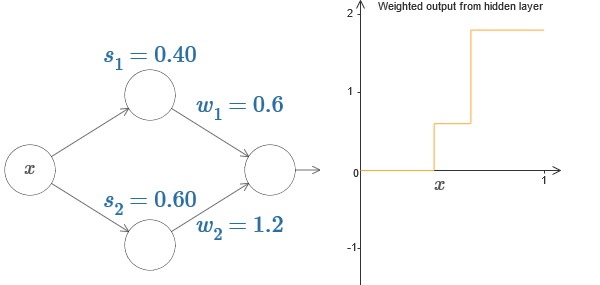
A la derecha hay un gráfico de la salida ponderada w ₁ a ₁ + w ₂ a _{2 de la} capa oculta. Aquí un ₁ y un ₂ son las salidas de las neuronas ocultas superior e inferior, respectivamente. Se denotan con "a", ya que a menudo se llaman activaciones neuronales.

Por cierto, notamos que la salida de toda la red es σ (w ₁ a ₁ + w ₂ a ₂ + b), donde b es el sesgo de la neurona de salida. Esto, obviamente, no es lo mismo que la salida ponderada de la capa oculta, cuyo gráfico estamos construyendo. Pero por ahora, nos concentraremos en la salida equilibrada de la capa oculta, y solo más adelante pensaremos en cómo se relaciona con la salida de toda la red.

Intente aumentar y disminuir el paso s _{1 de la} neurona oculta superior en el diagrama interactivo del artículo original . Vea cómo esto cambia la salida ponderada de la capa oculta. Es especialmente útil comprender qué sucede cuando s ₁ excede s ₂ . Verá que el gráfico en estos casos cambia de forma, a medida que pasamos de una situación en la que la neurona oculta superior se activa primero a una situación en la que la neurona oculta inferior se activa primero.

Del mismo modo, intente manipular el paso s _{2 de} la neurona oculta inferior y vea cómo esto cambia la producción general de las neuronas ocultas.

Intente reducir y aumentar los pesos de salida. Observe cómo esto escala la contribución de las neuronas ocultas correspondientes. ¿Qué sucede si uno de los pesos es igual a 0?

Finalmente, intente configurar w ₁ a 0.8 y w ₂ a -0.8. El resultado es una función de "protrusión", con un inicio en s ₁ , un final en s ₂ y una altura de 0.8. Por ejemplo, una salida ponderada podría verse así:



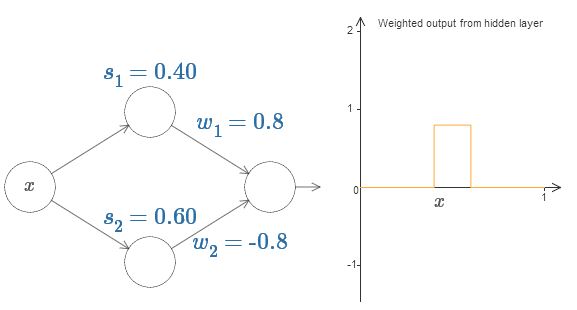
Por supuesto, la protuberancia se puede escalar a cualquier altura. Usemos un parámetro, h, que denota altura. Además, para simplificar, eliminaré la notación "s ₁ = ..." y "w ₁ = ...".



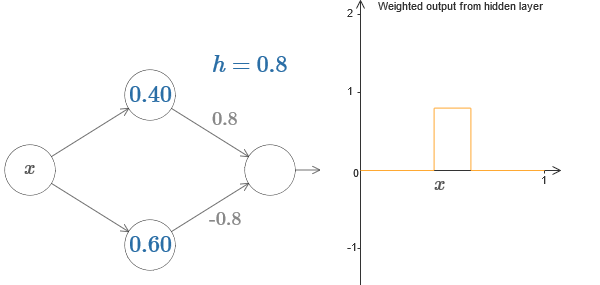
Intente aumentar y disminuir el valor h para ver cómo cambia la altura de la protuberancia. Intenta hacer h negativo. Intente cambiar los puntos de los pasos para observar cómo esto cambia la forma de la protuberancia.

Verá que usamos nuestras neuronas no solo como primitivas gráficas, sino también como unidades más familiares para los programadores, algo así como una instrucción if-then-else en programación:

si input> = inicio del paso:
agregue 1 a la salida ponderada
más:
agregue 0 a la salida ponderada

En su mayor parte, me atendré a la notación gráfica. Sin embargo, a veces será útil que cambie a la vista if-then-else y reflexione sobre lo que está sucediendo en estos términos.

Podemos usar nuestro truco de protrusión pegando dos partes de neuronas ocultas en la misma red:



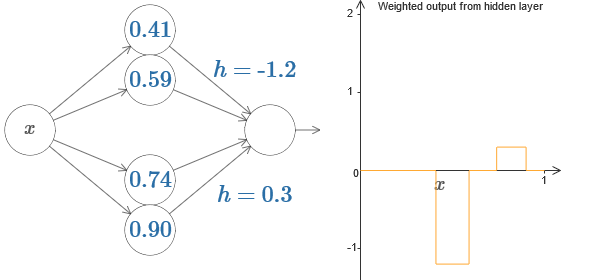
Aquí bajé los pesos simplemente escribiendo los valores h para cada par de neuronas ocultas. Intente jugar con ambos valores h y vea cómo cambia el gráfico. Mueva las pestañas, cambiando los puntos de los pasos.

En un caso más general, esta idea puede usarse para obtener cualquier número deseado de picos de cualquier altura. En particular, podemos dividir el intervalo [0,1] en un gran número de subintervalos (N), y usar N pares de neuronas ocultas para obtener picos de cualquier altura deseada. Veamos cómo funciona esto para N = 5. Esto ya es un montón de neuronas, así que soy una presentación un poco más estrecha. Perdón por el diagrama complejo: podría ocultar la complejidad detrás de abstracciones adicionales, pero me parece que vale la pena un poco de tormento con la complejidad para sentir mejor cómo funcionan las redes neuronales.



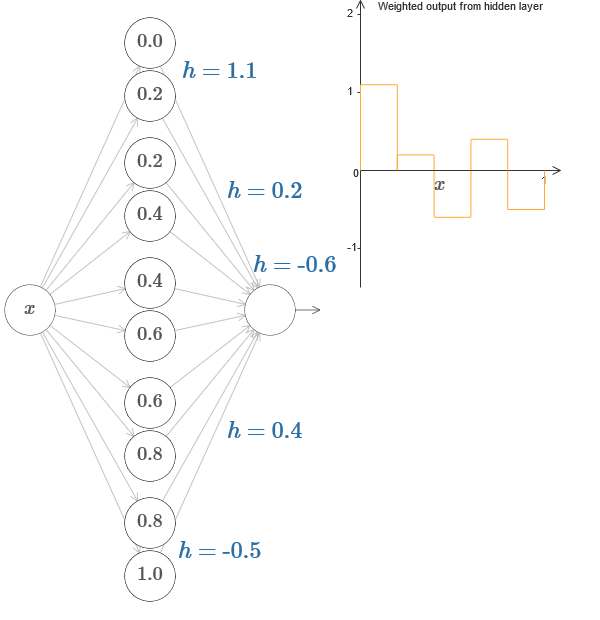
Verás, tenemos cinco pares de neuronas ocultas. Los puntos de los pasos de los pares correspondientes se encuentran en 0.1 / 5, luego 1 / 5.2 / 5, y así sucesivamente, hasta 4 / 5.5 / 5. Estos valores son fijos: obtenemos cinco protuberancias de igual ancho en el gráfico.

Cada par de neuronas tiene un valor h asociado a él. Recuerde que las conexiones neuronales de salida tienen pesos h y –h. En el artículo original en el gráfico, puede hacer clic en los valores h y moverlos de izquierda a derecha. Con un cambio de altura, el horario también cambia. ¡Al cambiar los pesos de salida, construimos la función final!

En el diagrama, aún puede hacer clic en el gráfico y arrastrar la altura de los pasos hacia arriba o hacia abajo. Cuando cambia su altura, ve cómo cambia la altura de la h correspondiente. Los pesos de salida + hy –h cambian en consecuencia. En otras palabras, manipulamos directamente una función cuyo gráfico se muestra a la derecha y vemos estos cambios en los valores de h a la izquierda. También puede mantener presionado el botón del mouse sobre una de las protuberancias, y luego arrastrar el mouse hacia la izquierda o hacia la derecha, y las protuberancias se ajustarán a la altura actual.

Es hora de hacer el trabajo.

Recordemos la función que dibujé al comienzo del capítulo:



Entonces no mencioné esto, pero de hecho se ve así:

$$

$$f (x) = 0.2 + 0.4 x ^ 2 + 0.3x \ sin (15 x) + 0.05 \ cos (50 x) \ tag {113}$$

Se construye para valores x de 0 a 1, y los valores a lo largo del eje y varían de 0 a 1.

Obviamente, esta función no es trivial. Y tienes que descubrir cómo calcularlo usando redes neuronales.

En nuestras redes neuronales anteriores, analizamos una combinación ponderada ∑ _j w _j a _j de salida neuronal oculta. Sabemos cómo obtener un control significativo sobre este valor. Pero, como señalé anteriormente, este valor no es igual a la salida de la red. La salida de la red es σ (∑ _j w _j a _j + b), donde b es el desplazamiento de la neurona de salida. ¿Podemos obtener el control directamente sobre la salida de la red?

La solución es desarrollar una red neuronal en la que la salida ponderada de la capa oculta esté dada por la ecuación σ ⁻¹ ⋅f (x), donde σ ⁻¹ es la función inversa de σ. Es decir, queremos que la salida ponderada de la capa oculta sea así:



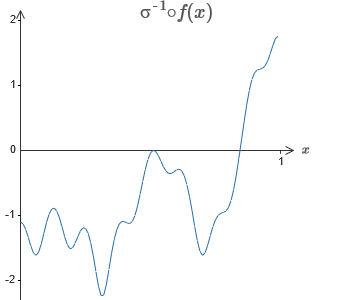Si esto tiene éxito, entonces la salida de toda la red será una buena aproximación de f (x) (configuré el desplazamiento de la neurona de salida a 0).

Entonces su tarea es desarrollar un NS que se aproxime a la función objetivo que se muestra arriba. Para comprender mejor lo que está sucediendo, le recomiendo que resuelva este problema dos veces. Por primera vez en el artículo original, haga clic en el gráfico y ajuste directamente las alturas de las diferentes protuberancias. Será bastante fácil para usted obtener una buena aproximación a la función objetivo. El grado de aproximación se estima por la desviación promedio, la diferencia entre la función objetivo y la función que calcula la red. Su tarea es llevar la desviación promedio a un valor mínimo. La tarea se considera completada cuando la desviación promedio no excede 0.40.



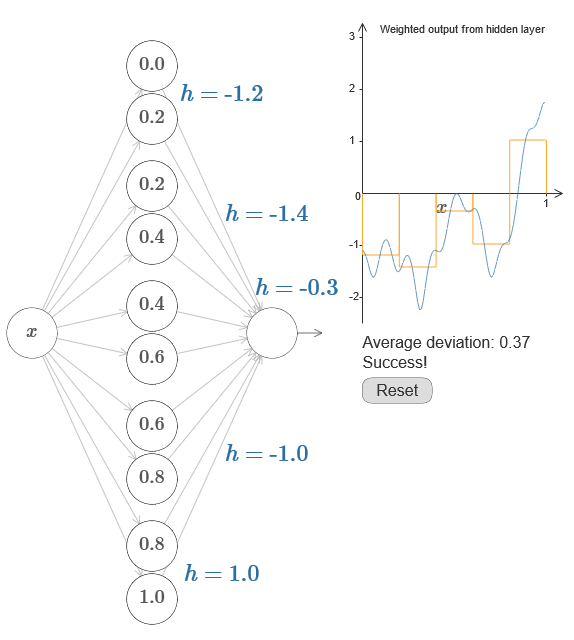Después de lograr el éxito, presione el botón Restablecer, que cambia aleatoriamente las pestañas. La segunda vez, no toque el gráfico, pero cambie los valores h en el lado izquierdo del diagrama, tratando de llevar la desviación promedio a un valor de 0.40 o menos.

¡Entonces, ha encontrado todos los elementos necesarios para que la red calcule aproximadamente la función f (x)! La aproximación resultó ser aproximada, pero podemos mejorar fácilmente el resultado simplemente aumentando el número de pares de neuronas ocultas, lo que aumentará el número de protuberancias.

En particular, es fácil convertir todos los datos encontrados en la vista estándar con la parametrización utilizada para NS. Déjame recordarte rápidamente cómo funciona esto.

En la primera capa, todos los pesos tienen un valor constante grande, por ejemplo, w = 1000.

Los desplazamientos de las neuronas ocultas se calculan a través de b = −ws. Entonces, por ejemplo, para la segunda neurona oculta, s = 0.2 se convierte en b = −1000 × 0.2 = −200.

La última capa de la escala está determinada por los valores de h. Entonces, por ejemplo, el valor que seleccionó para la primera h, h = -0.2, significa que los pesos de salida de las dos neuronas ocultas superiores son -0.2 y 0.2, respectivamente. Y así sucesivamente, para toda la capa de pesos de salida.

Finalmente, el desplazamiento de la neurona de salida es 0.

Y eso es todo: obtuvimos una descripción completa del NS, que calcula bien la función objetivo inicial. Y entendemos cómo mejorar la calidad de la aproximación mejorando la cantidad de neuronas ocultas.

Además, en nuestra función objetivo original f (x) = 0.2 + 0.4x ²+ 0.3sin (15x) + 0.05cos (50x) no es nada especial. Se podría utilizar un procedimiento similar para cualquier función continua en los intervalos de [0,1] a [0,1]. De hecho, usamos nuestro NS de una sola capa para construir una tabla de búsqueda para una función. Y podemos tomar esta idea como base para obtener una prueba generalizada de universalidad.

Función de muchos parámetros

Extendemos nuestros resultados al caso de un conjunto de variables de entrada. Suena complicado, pero todas las ideas que necesitamos ya se pueden entender para el caso con solo dos variables entrantes. Por lo tanto, consideramos el caso con dos variables entrantes.

Comencemos mirando lo que sucede cuando una neurona tiene dos entradas: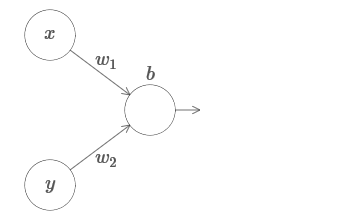



tenemos entradas x e y, con los pesos correspondientes w ₁ y w ₂ y compensación b de la neurona. Establecemos el peso de w ₂ en 0 y jugamos con el primero, w ₁ , y compensamos b para ver cómo afectan la salida de la neurona:



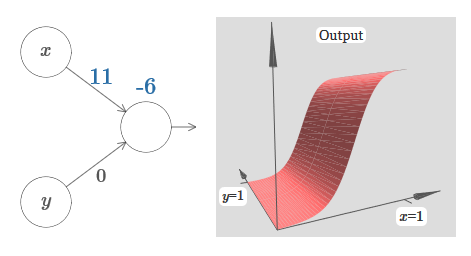Como puede ver, con w ₂ = 0, la entrada y no afecta la salida de la neurona. Todo sucede como si x es la única entrada.

Dado esto, ¿qué crees que sucederá cuando aumentemos el peso de w ₁ a w ₁ = 100 y w ₂ deje 0? Si esto no le resulta claro de inmediato, piense un poco sobre este tema. Luego mire el siguiente video, que muestra lo que sucederá:



Como antes, con un aumento en el peso de entrada, la salida se acerca a la forma del paso. La diferencia es que nuestra función de paso ahora se encuentra en tres dimensiones. Como antes, podemos mover la ubicación de los pasos cambiando el desplazamiento. El ángulo estará en el punto s _x ≡ - b / w1.

Vamos a rehacer el diagrama para que el parámetro sea la ubicación del paso:



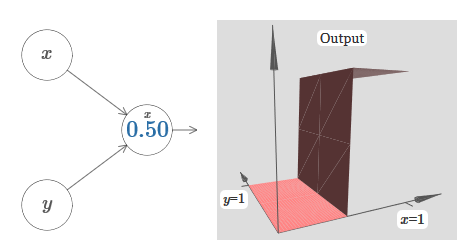suponemos que el peso de entrada de x es de gran importancia: utilicé w ₁ = 1000 y el peso w ₂ = 0. El número en la neurona es la posición del paso, y la x de arriba nos recuerda que movemos el paso a lo largo del eje x. Naturalmente, es bastante posible obtener una función de paso a lo largo del eje y, haciendo que el peso entrante para y sea grande (por ejemplo, w ₂= 1000), y el peso para x es 0, w ₁ = 0:



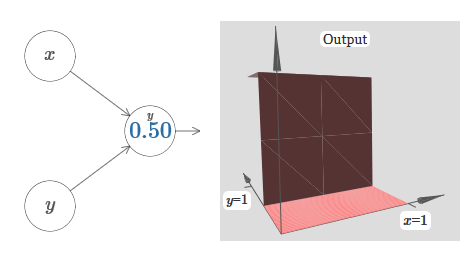el número en la neurona, nuevamente, indica la posición del paso, yy encima nos recuerda que movemos el paso a lo largo del eje y. Pude designar directamente los pesos para x e y, pero no lo hice, porque eso ensuciaría el gráfico. Pero tenga en cuenta que el marcador y indica que el peso para y es grande y para x es 0.

Podemos usar las funciones de pasos que acabamos de diseñar para calcular la función de protrusión tridimensional. Para hacer esto, tomamos dos neuronas, cada una de las cuales calculará una función de paso a lo largo del eje x. Luego combinamos estas funciones de paso con los pesos h y –h, donde h es la altura de protuberancia deseada. Todo esto se puede ver en el siguiente diagrama:



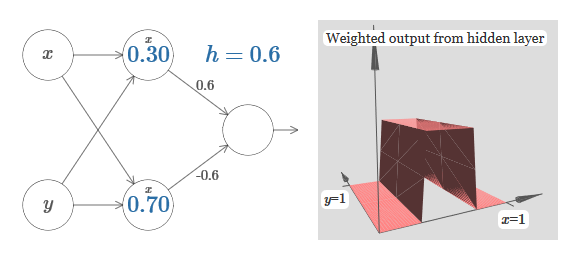Intenta cambiar el valor de h. Vea cómo se relaciona con los pesos de la red. Y cómo cambia la altura de la función de protrusión a la derecha.

También intente cambiar el punto del paso, cuyo valor se establece en 0,30 en la neurona oculta superior. Vea cómo cambia la forma de la protuberancia. ¿Qué sucede si lo mueve más allá del punto 0.70 asociado con la neurona oculta inferior?

Aprendimos a construir la función de protrusión a lo largo del eje x. Naturalmente, podemos hacer que la protuberancia funcione fácilmente a lo largo del eje y, utilizando funciones de dos pasos a lo largo del eje y. Recuerde que podemos hacer esto haciendo grandes pesos en la entrada y, y configurando el peso 0 en la entrada x. Y entonces, qué pasa:



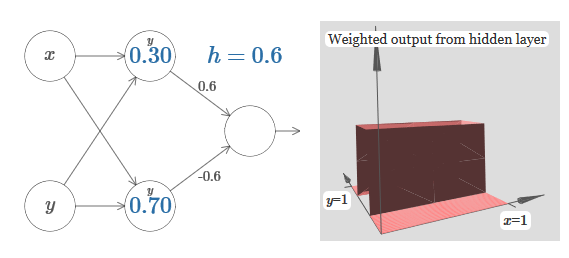¡Se ve casi idéntico a la red anterior! El único cambio visible son pequeños marcadores y en neuronas ocultas. Nos recuerdan que producen funciones escalonadas para y, y no para x, por lo que el peso en la entrada y es muy grande, y en la entrada x es cero, y no al revés. Como antes, decidí no mostrarlo directamente, para no saturar la imagen.

Veamos qué sucede si agregamos dos funciones de protrusión, una a lo largo del eje x, la otra a lo largo del eje y, ambas de altura h:



para simplificar el diagrama de conexión con peso cero, omití. Hasta ahora, he dejado pequeños marcadores x e y en neuronas ocultas para recordar en qué direcciones se calculan las funciones de protrusión. Más tarde los rechazaremos, ya que están implicados por la variable entrante.

Intente cambiar el parámetro h. Como puede ver, debido a esto, los pesos de salida cambian, así como los pesos de ambas funciones de protrusión, x e y.

Nuestra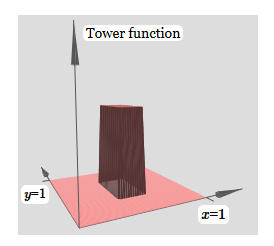



creación es un poco como una "función de torre": si podemos crear tales funciones de torre, podemos usarlas para aproximar funciones arbitrarias simplemente agregando torres de varias alturas en diferentes lugares:



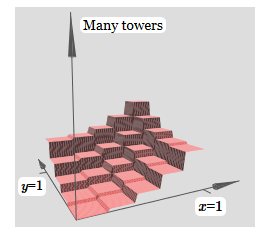Por supuesto, aún no hemos llegado a la creación de una función de torre arbitraria. Hasta ahora, hemos construido algo así como una torre central de altura 2h con una meseta de altura h que la rodea.

Pero podemos hacer que una torre funcione. Recuerde que previamente mostramos cómo se pueden usar las neuronas para implementar la declaración if-then-else:

if  >= :  1 else:  0 

Era una neurona de una entrada. Y necesitamos aplicar una idea similar a la salida combinada de neuronas ocultas:

  if     >= :  1 else:  0 

Si elegimos el umbral correcto, por ejemplo, 3h / 2, apretado entre la altura de la meseta y la altura de la torre central, podemos aplastar la meseta a cero y dejar solo una torre.

Imagina cómo hacer esto? Intenta experimentar con la siguiente red. Ahora estamos trazando la salida de toda la red, y no solo la salida ponderada de la capa oculta. Esto significa que agregamos el término de compensación a la salida ponderada de la capa oculta y aplicamos el sigmoide. ¿Puedes encontrar los valores para h y b para los que obtienes una torre? Si se atasca en este punto, aquí hay dos consejos: (1) para que la neurona saliente demuestre el comportamiento correcto en el estilo if-then-else, necesitamos que los pesos entrantes (todos h o –h) sean grandes; (2) el valor de b determina la escala del umbral if-then-else.



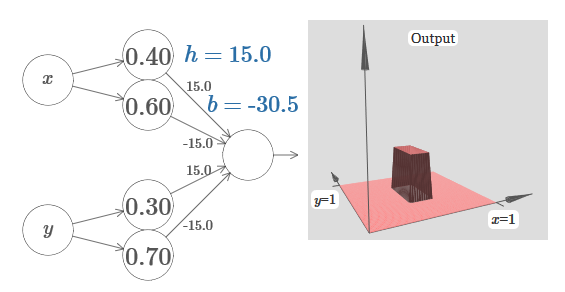
Con los parámetros predeterminados, la salida es similar a una versión aplanada del diagrama anterior, con una torre y una meseta. Para obtener el comportamiento deseado, debe aumentar el valor de h. Esto nos dará el comportamiento umbral de if-then-else. En segundo lugar, para establecer correctamente el umbral, uno debe elegir b ≈ −3h / 2.

Esto es lo que parece para h = 10:


Incluso para valores relativamente modestos de h, obtenemos una buena función de torre. Y, por supuesto, podemos obtener un resultado arbitrariamente hermoso aumentando h aún más y manteniendo el sesgo en el nivel b = −3h / 2.

Intentemos unir dos redes para contar dos funciones de torre diferentes. Para aclarar las funciones respectivas de las dos subredes, las coloco en rectángulos separados: cada una de ellas calcula la función de la torre utilizando la técnica descrita anteriormente. El gráfico de la derecha muestra la salida ponderada de la segunda capa oculta, es decir, la combinación ponderada de las funciones de la torre.



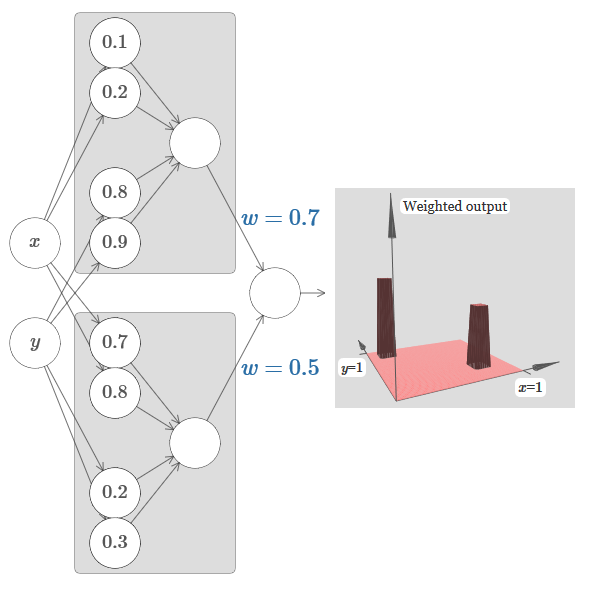
En particular, se puede ver que al cambiar el peso en la última capa, puede cambiar la altura de las torres de salida.

La misma idea le permite calcular tantas torres como desee. Podemos hacerlos arbitrariamente delgados y altos. Como resultado, garantizamos que la salida ponderada de la segunda capa oculta se aproxima a cualquier función deseada de dos variables:



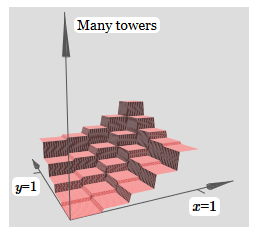
En particular, al hacer que la salida ponderada de la segunda capa oculta se aproxime bien a σ ⁻¹ ⋅f, garantizamos que la salida de nuestra red será una buena aproximación de la función deseada f.

¿Qué pasa con las funciones de muchas variables?

Tratemos de tomar tres variables, x ₁ , x ₂ , x ₃ . ¿Se puede usar la siguiente red para calcular la función de la torre en cuatro dimensiones?



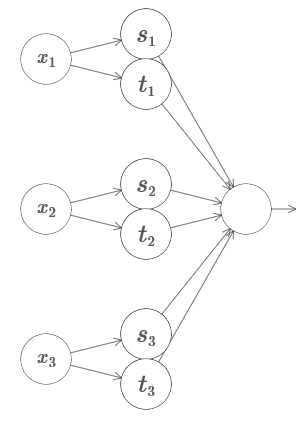
Aquí x ₁ , x ₂ , x ₃ denotan la entrada de red. s ₁ , t _1, y así sucesivamente: puntos de paso para las neuronas, es decir, todos los pesos en la primera capa son grandes, y los desplazamientos se asignan de modo que los puntos de los pasos sean s ₁ , t ₁ , s ₂ , ... Los pesos en la segunda capa se alternan, + h, −h, donde h es un número muy grande. El desplazamiento de salida es −5h / 2.

La red calcula una función igual a 1 en tres condiciones: x ₁ está entre s ₁ y t ₁ ; x ₂ está entre s ₂ y t ₂ ; x ₃ está entre s ₃ y t ₃ . La red es 0 en todos los demás lugares. Esta es una torre en la que 1 es una pequeña porción del espacio de entrada, y 0 es todo lo demás.

Al pegar muchas de esas redes, podemos obtener tantas torres como queramos y aproximar una función arbitraria de tres variables. La misma idea funciona en m dimensiones. Solo el desplazamiento de salida (−m + 1/2) h se cambia para exprimir adecuadamente los valores deseados y eliminar la meseta.

Bueno, ahora sabemos cómo usar NS para aproximar la función real de muchas variables. ¿Qué pasa con las funciones vectoriales f (x ₁ , ..., x _m ) ∈ R ⁿ ? Por supuesto, dicha función puede considerarse simplemente como n funciones reales separadas f1 (x ₁ , ..., x _m ), f2 (x ₁ , ..., x _m ), y así sucesivamente. Y luego simplemente pegamos todas las redes juntas. Así que es fácil resolverlo.

Desafío

• Vimos cómo usar redes neuronales con dos capas ocultas para aproximar una función arbitraria. ¿Puedes demostrar que esto es posible con una capa oculta? Sugerencia: intente trabajar con solo dos variables de salida y demuestre que: (a) es posible obtener las funciones de los pasos no solo a lo largo de los ejes x o y, sino también en una dirección arbitraria; (b) sumando muchas construcciones del paso (a), es posible aproximar la función de una torre redonda en lugar de una torre rectangular; © utilizando torres redondas, es posible aproximar una función arbitraria. El paso © será más fácil de hacer usando el material presentado en este capítulo un poco más abajo.

Ir más allá de las neuronas sigmoideas

Hemos demostrado que una red de neuronas sigmoideas puede calcular cualquier función. Recuerde que en una neurona sigmoidea, las entradas x ₁ , x ₂ , ... se convierten en la salida en σ (∑ _j w _j x _{j j} + b), donde w _j son los pesos, b es el sesgo y σ es el sigmoide.



¿Qué sucede si observamos otro tipo de neurona usando una función de activación diferente, s (z):



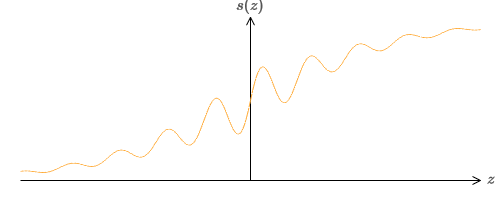
Es decir, suponemos que si una neurona tiene x ₁ , x ₂ , ... pesos w ₁ , w ₂ , ... y sesgo b, entonces se generará s (∑ _j w _j x _j + b).

Podemos usar esta función de activación para avanzar, al igual que en el caso del sigmoide. Pruebe (en el artículo original ) en el diagrama para levantar el peso, por ejemplo, w = 100:





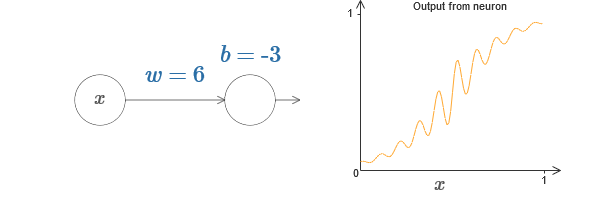
Como en el caso del sigmoide, debido a esto, la función de activación se comprime y, como resultado, se convierte en una muy buena aproximación de la función de paso. Intente cambiar el desplazamiento, y verá que podemos cambiar la ubicación del paso a cualquiera. Por lo tanto, podemos usar los mismos trucos que antes para calcular cualquier función deseada.

¿Qué propiedades debe tener s (z) para que esto funcione? Debemos suponer que s (z) está bien definido como z → −∞ y z → ∞. Estos límites son dos valores aceptados por nuestra función de paso. También debemos suponer que estos límites son diferentes. Si no fueran diferentes, los pasos no funcionarían; ¡simplemente habría un horario fijo! Pero si la función de activación s (z) satisface estas propiedades, las neuronas basadas en ella son universalmente adecuadas para los cálculos.

Las tareas

• Anteriormente en el libro, conocimos un tipo diferente de neurona: una neurona lineal enderezada o una unidad lineal rectificada, ReLU. Explica por qué tales neuronas no satisfacen las condiciones necesarias para la universalidad. Encuentre evidencia de versatilidad que demuestre que las ReLU son universalmente adecuadas para la informática.
• Supongamos que estamos considerando neuronas lineales, con la función de activación s (z) = z. Explica por qué las neuronas lineales no satisfacen las condiciones de universalidad. Muestre que tales neuronas no pueden usarse para la computación universal.

Fix step function

Por el momento, asumimos que nuestras neuronas producen funciones escalonadas precisas. Esta es una buena aproximación, pero solo una aproximación. De hecho, hay una brecha estrecha de falla, que se muestra en el siguiente gráfico, donde las funciones no se comportan en absoluto como una función de paso:



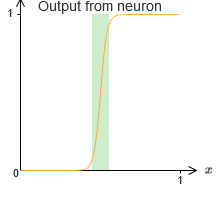
En este período de fracaso, mi explicación de la universalidad no funciona.

El fracaso no es tan aterrador. Al establecer pesos de entrada suficientemente grandes, podemos hacer que estas brechas sean arbitrariamente pequeñas. Podemos hacerlos mucho más pequeños que en el gráfico, invisibles a la vista. Entonces quizás no tengamos que preocuparnos por este problema.

Sin embargo, me gustaría tener alguna forma de resolverlo.

Resulta que es fácil de resolver. Veamos esta solución para calcular funciones NS con solo una entrada y salida. Las mismas ideas funcionarán para resolver el problema con una gran cantidad de entradas y salidas.

En particular, supongamos que queremos que nuestra red calcule alguna función f. Como antes, intentamos hacer esto diseñando la red de manera que la salida ponderada de la capa oculta de neuronas sea σ ⁻¹ ⋅f (x):



Si hacemos esto usando la técnica descrita anteriormente, forzaremos a las neuronas ocultas a producir una secuencia de funciones de protrusión:



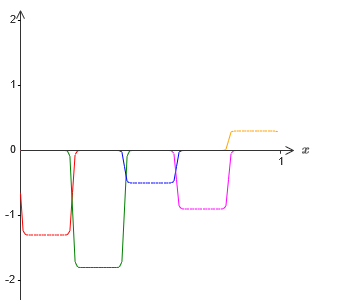
Por supuesto, exageré el tamaño de los intervalos de falla, para que fuera más fácil de ver. Debe quedar claro que si sumamos todas estas funciones de las protuberancias, obtenemos una aproximación bastante buena de σ ⁻¹ ⋅f (x) en todas partes, excepto los intervalos de falla.

Pero, supongamos que en lugar de usar la aproximación que acabamos de describir, usamos un conjunto de neuronas ocultas para calcular la aproximación de la mitad de nuestra función objetivo original, es decir, σ ⁻¹ ⋅f (x) / 2. Por supuesto, se verá como una versión a escala del último gráfico:



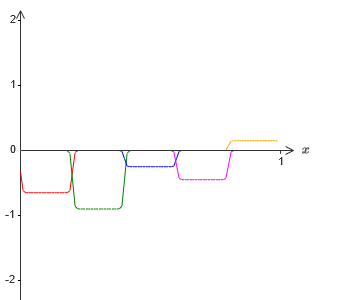
Y, supongamos que hacemos que un conjunto más de neuronas ocultas calcule la aproximación a σ ⁻¹ ⋅f (x) / 2, sin embargo, en su base las protuberancias se desplazarán a la mitad de su ancho:



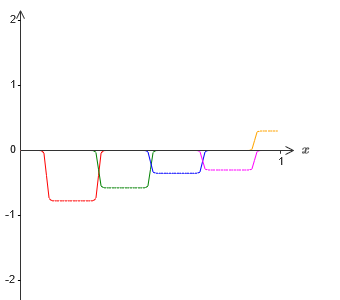
Ahora tenemos dos aproximaciones diferentes para σ - 1⋅f (x) / 2. Si sumamos estas dos aproximaciones, obtenemos una aproximación general a σ - 1⋅f (x). Esta aproximación general todavía tendrá imprecisiones en pequeños intervalos. Pero el problema será menor que antes, porque los puntos que caen en los intervalos de falla de la primera aproximación no caerán en los intervalos de falla de la segunda aproximación. Por lo tanto, la aproximación en estos intervalos será aproximadamente 2 veces mejor.

Podemos mejorar la situación agregando un gran número, M, de aproximaciones superpuestas de la función σ - 1⋅f (x) / M. Si todos sus intervalos de falla son lo suficientemente estrechos, cualquier corriente estará en solo uno de ellos. Si utiliza un número suficientemente grande de aproximaciones superpuestas de M, el resultado es una aproximación general excelente.

Conclusión

¡La explicación de universalidad discutida aquí definitivamente no puede llamarse una descripción práctica de cómo contar funciones usando redes neuronales! En este sentido, es más como una prueba de la versatilidad de las puertas lógicas NAND y más. Por lo tanto, básicamente intenté hacer que este diseño sea claro y fácil de seguir sin optimizar sus detalles. Sin embargo, tratar de optimizar este diseño puede ser un ejercicio interesante e instructivo para usted.

Aunque el resultado obtenido no se puede usar directamente para crear NS, es importante porque elimina la cuestión de la computabilidad de cualquier función particular que use NS. La respuesta a esa pregunta siempre será positiva. Por lo tanto, es correcto preguntar si alguna función es computable, pero cuál es la forma correcta de calcularla.

Nuestro diseño universal usa solo dos capas ocultas para calcular una función arbitraria. Como discutimos, es posible obtener el mismo resultado con una sola capa oculta. Dado esto, puede preguntarse por qué necesitamos redes profundas, es decir, redes con una gran cantidad de capas ocultas. ¿No podemos simplemente reemplazar estas redes por otras poco profundas que tienen una capa oculta?

Aunque, en principio, es posible, existen buenas razones prácticas para utilizar redes neuronales profundas. Como se describe en el Capítulo 1, los NS profundos tienen una estructura jerárquica que les permite adaptarse bien para estudiar el conocimiento jerárquico, que son útiles para resolver problemas reales. Más específicamente, cuando se resuelven problemas como el reconocimiento de patrones, es útil usar un sistema que comprenda no solo píxeles individuales, sino también conceptos cada vez más complejos: desde bordes hasta formas geométricas simples, y más allá, hasta escenas complejas que involucran varios objetos. En capítulos posteriores veremos evidencia a favor del hecho de que las NS profundas serán más capaces de hacer frente al estudio de tales jerarquías de conocimiento que las superficiales. Para resumir: la universalidad nos dice que NS puede calcular cualquier función; La evidencia empírica sugiere que los NS profundos se adaptan mejor al estudio de funciones útiles para resolver muchos problemas del mundo real.