Nuevo método de análisis de clúster

Se propone un nuevo método de análisis de conglomerados. Su ventaja está en un algoritmo menos complejo computacionalmente. El método se basa en el cálculo de votos por el hecho de que un par de objetos está en la misma clase a partir de la información sobre el valor de las coordenadas individuales.

Introduccion

Una gran necesidad de análisis de datos es el desarrollo de métodos de clasificación efectivos. En tales métodos, se requiere dividir todo el conjunto de objetos en el número óptimo de clases, basándose únicamente en la información sobre el valor de los indicadores individuales [Zagoruyko 1999].

El análisis de conglomerados es uno de los métodos más populares de análisis de datos y estadísticas matemáticas. El análisis de conglomerados le permite encontrar automáticamente clases de objetos, utilizando solo información sobre los indicadores cuantitativos de los objetos (capacitación sin un maestro). Cada una de estas clases puede definirse por uno de sus objetos más característicos, por ejemplo, el promedio en términos de indicadores. Hay una gran cantidad de métodos y enfoques para clasificar datos.

La investigación moderna en el campo del análisis de conglomerados se lleva a cabo para mejorar los métodos para determinar las clases de topología compleja [Furaoa 2007, Zagoruiko 2013], así como para mejorar la velocidad de los algoritmos en el caso de grandes datos.

En este artículo, proponemos un método de clasificación basado en la obtención de votos para un par de objetos en la misma clase, basado en información sobre el valor de los indicadores individuales. Se propone considerar que un par de objetos está en la misma clase si los valores de sus indicadores individuales están en el intervalo con una longitud que no excede un valor dado.

Método K-means

El método k-means es uno de los métodos de agrupamiento más populares. Su propósito es obtener dichos centros de datos que correspondan a la hipótesis de compacidad de las clases de datos con su distribución radial simétrica. Una forma de determinar las posiciones de dichos centros, dado su número \ textit {k}, es el enfoque EM.

En este método, se realizan dos procedimientos secuencialmente.

1. Definición para cada objeto de datos$$ $ en línea $ X_ {i} $ en línea $ el centro mas cercano$$ $ en línea $ C_ {j} $ en línea $ y asignar una etiqueta de clase a este objeto$$ $ en línea $ X_ {i} ^ {j} $ en línea $ . Además, para todos los objetos, su pertenencia a diferentes clases se determina.
2. Cálculo de la nueva posición de los centros de todas las clases.

Repitiendo iterativamente estos dos procedimientos desde la posición aleatoria inicial de los centros de las clases \ textit {k}, podemos lograr la separación de los objetos en clases que correspondan más estrechamente a la hipótesis de la compacidad radial de las clases.

El algoritmo de clasificación de un nuevo autor se comparará con el método k-means.

Nuevo metodo

El nuevo algoritmo de análisis de conglomerados se basa en los votos para pertenecer a diferentes conglomerados a partir de información sobre los valores de las coordenadas individuales de los puntos de datos.

1. Se especifica un valor d que caracteriza la longitud del intervalo de indicadores dentro del cual se considera que dos objetos pertenecen a la misma clase.
2. Métrica seleccionada$$ $ en línea $ x_ {i} $ en línea $ y todos los pares de objetos son considerados$$ $ en línea $ \ left \ {O_ {l}, O_ {k} \ right \} $ en línea $ donde$$ $ en línea $ l, k = 1 \ ldots N $ en línea $ .
3. Si$$ $ en línea $ \ left | x_ {i} ^ {l} -x_ {i} ^ {k} \ right | \ le d $ en línea $ entonces la magnitud$$ $ en línea $ r_ {lk}: = r_ {lk} + 1 $ en línea $ (voz agregada).
4. Las acciones 2) y 3) se repiten para todos los indicadores$$ $ en línea $ i = 1 \ ldots M $ en línea $ .
5. Se establece el valor p que caracteriza el número mínimo de votos para pertenecer a las mismas clases.
6. Usando el método clave de pares de valores, se determinan todas las clases de objetos, de modo que dentro de una clase de voz para pares de objetos de estas clases > = p .
7. Repite todos los valores de d y p y repite los elementos 1) - 6) para obtener el número de clases más cercano al número dado de clases g .

Para reducir la complejidad del algoritmo a N , puede usar intervalos T para indicadores individuales y reemplazar las cláusulas 2) y 3) en el algoritmo con lo siguiente:

1. El indicador está seleccionado$$ $ en línea $ x_ {i} $ en línea $ y se consideran todos los intervalos$$ $ en línea $ \ left [u_ {l}, w_ {l} \ right] $ en línea $ donde$$ $ en línea $ l = 1 \ ldots T $ en línea $ :

$$$$ display $$ u_ {0} = \ min (x_ {i}); u_ {0} = \ min (x_ {i}); $$ display $$

$$$$ display $$ w_ {T} = \ max (x_ {i}); $$ display $$

$$$$ display $$ s_ {i} = w_ {T} -u_ {0}; $$ display $$

$$$$ display $$ u_ {l} = u_ {0} + l \ cdot s_ {i}; $$ display $$

$$$$ display $$ w_ {l} = u_ {l} + d; $$ display $$

2. Si$$ $ en línea $ x_ {i} ^ {k} \ in \ left [u_ {j}, w_ {j} \ right] $ en línea $ y$$ $ en línea $ x_ {i} ^ {l} \ in \ left [u_ {j}, w_ {j} \ right] $ en línea $ donde$$ $ en línea $ j = 1 \ ldots T $ en línea $ entonces la magnitud$$ $ en línea $ r_ {lk}: = r_ {lk} + 1 $ en línea $ (la voz se agrega con una tecla única l , k para el i- ésimo indicador).

Experimento numérico

Los datos con la clasificación intuitiva para los humanos se tomaron como datos iniciales.

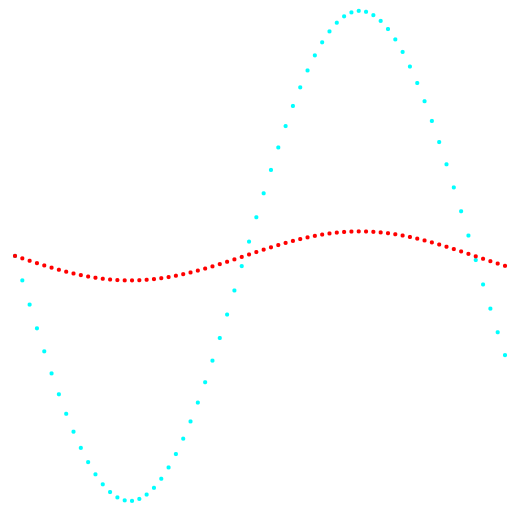
Las Figuras 1 y 2 muestran los resultados de la clasificación del método k-medias y el nuevo método de clasificación.


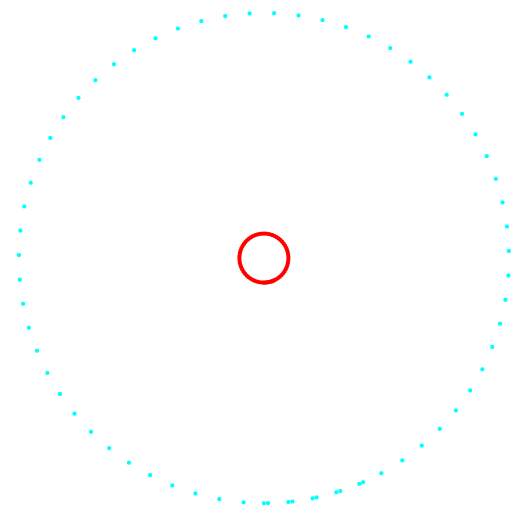Fig. 1. Proyección 1-2 y clasificación de datos.

A la izquierda está el método k-means, a la derecha está el método del autor.


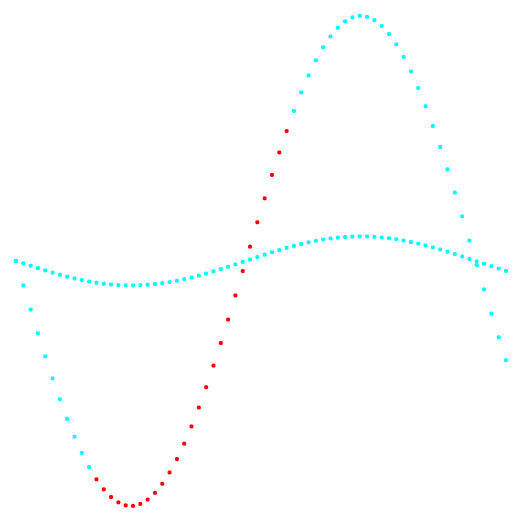
Fig. 2. Proyección 2-3 y clasificación de datos.

A la izquierda está el método k-means, a la derecha está el método del autor.

El resultado de comparar los dos métodos muestra la ventaja obvia del método del autor en su capacidad para detectar grupos de topología compleja.

Implementación de software

El método de agrupación de k-means se implementó mediante programación como una aplicación web. La parte informática de la aplicación se envía a un servidor escrito en PHP usando el marco Zend. La interfaz de la aplicación está escrita con HTML, CSS, JavaScript, jQuery. La aplicación está disponible en http://svlaboratory.org/application/klaster2 después de registrar un nuevo usuario. La aplicación le permite visualizar la pertenencia de objetos a diferentes grupos en un plano de coordenadas dado.

Conclusión

Se propone un nuevo método de clasificación. Las ventajas de este método son el reconocimiento de clases de topología compleja, distribución no radial, así como una menor complejidad del algoritmo y menos acciones, lo que es especialmente beneficioso en el caso de grandes conjuntos de datos.

Referencias

1. Zagoruyko N.G. Métodos aplicados de análisis de datos y conocimientos. Novosibirsk: Editorial del Instituto de Matemáticas, 1999.270 p.
2. Zagoruyko N.G., Borisova I.A., Kutnenko O.A., Levanov D.A. Detección de patrones en matrices de datos experimentales // Tecnologías computacionales. - 2013.Vol. 18. No. S1. S. 12-20.
3. Shen Furaoa, Tomotaka Ogurab, Osamu Hasegawab Una red neuronal incremental autoorganizada mejorada para el aprendizaje en línea sin supervisión. Laboratorio Hasegawa, 2007.