La traducción fue preparada para los estudiantes del curso "Análisis aplicado en R" .
Este fue mi primer intento de agrupar clientes basados en datos reales, y me dio una experiencia valiosa. Hay muchos artículos en Internet sobre la agrupación en clúster utilizando variables numéricas, pero encontrar soluciones para datos categóricos, que es algo más difícil, no fue tan simple. Los métodos de agrupamiento para datos categóricos todavía están en desarrollo, y en otra publicación voy a probar con otro.
Por otro lado, muchas personas piensan que agrupar datos categóricos puede no producir resultados significativos, y esto es en parte cierto (ver la
excelente discusión sobre CrossValidated ). En un momento, pensé: “¿Qué estoy haciendo? Simplemente se pueden dividir en cohortes ". Sin embargo, el análisis de cohortes tampoco siempre es aconsejable, especialmente con un número significativo de variables categóricas con una gran cantidad de niveles: puede manejar fácilmente de 5 a 7 cohortes, pero si tiene 22 variables y cada una tiene 5 niveles (por ejemplo, una encuesta de clientes con estimaciones discretas 1 , 2, 3, 4 y 5), y necesita comprender con qué grupos característicos de clientes está tratando: obtendrá cohortes de 22x5. Nadie quiere molestarse con tal tarea. Y aquí la agrupación podría ayudar. Entonces, en esta publicación, hablaré sobre lo que a mí mismo me gustaría saber tan pronto como comience a agrupar.
El proceso de agrupación en sí consta de tres pasos:
- Construir una matriz de disimilitud es, sin duda, la decisión más importante en la agrupación. Todos los pasos posteriores se basarán en la matriz de disimilitud que creó.
- La elección del método de agrupamiento.
- Evaluación de clúster.
Esta publicación será una especie de introducción que describe los principios básicos de la agrupación y su implementación en el entorno R.
Matriz de disimilitud
La base para la agrupación será la matriz de disimilitud, que en términos matemáticos describe la diferencia entre los puntos del conjunto de datos. Le permite combinar aún más en los grupos aquellos puntos que están más cercanos entre sí, o separar los más distantes entre sí; esta es la idea principal de la agrupación.
En esta etapa, las diferencias entre los tipos de datos son importantes, ya que la matriz de disimilitud se basa en las distancias entre puntos de datos individuales. Es fácil imaginar las distancias entre los puntos de datos numéricos (un ejemplo bien conocido son las
distancias euclidianas ), pero en el caso de los datos categóricos (factores en R), no todo es tan obvio.
Para construir una matriz de disimilitud en este caso, se debe utilizar la llamada distancia de Gover. No profundizaré en la parte matemática de este concepto, simplemente proporcionaré enlaces:
aquí y
allá . Para esto, prefiero usar
daisy() con la
metric = c("gower") del paquete del
cluster .
La matriz de disimilitud está lista. Para 200 observaciones, se construye rápidamente, pero puede requerir una gran cantidad de cómputo si se trata de un conjunto de datos grande.
En la práctica, es muy probable que primero tenga que limpiar el conjunto de datos, realizar las transformaciones necesarias de las filas en factores y rastrear los valores faltantes. En mi caso, el conjunto de datos también contenía filas de valores perdidos que se agrupaban maravillosamente cada vez, por lo que parecía que era un tesoro, hasta que miré los valores (¡ay!).
Algoritmos de agrupamiento
Es posible que ya sepa que la agrupación es
k-means y jerárquica . En esta publicación, me concentro en el segundo método, ya que es más flexible y permite varios enfoques: puede elegir un algoritmo de agrupamiento
aglomerativo (de abajo hacia arriba) o
divisional (de arriba hacia abajo).
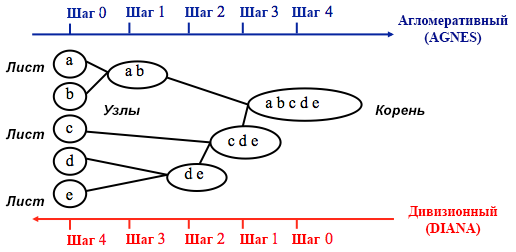Fuente: Guía de programación de UC Business Analytics RLa agrupación aglomerativa comienza con
n agrupaciones, donde
n es el número de observaciones: se supone que cada una de ellas es una agrupación separada. Luego, el algoritmo intenta encontrar y agrupar los puntos de datos más similares entre ellos; así es como comienza la formación de conglomerados.
La agrupación divisional se realiza de manera opuesta: inicialmente se supone que todos los n puntos de datos que tenemos son un grupo grande, y luego los menos similares se dividen en grupos separados.
Al decidir cuál de estos métodos elegir, siempre tiene sentido probar todas las opciones, sin embargo, en general, la
agrupación aglomerativa es mejor para identificar grupos pequeños y es utilizada por la mayoría de los programas de computadora, y la agrupación divisional es más apropiada para identificar grupos grandes .
Personalmente, antes de decidir qué método usar, prefiero mirar los dendrogramas, una representación gráfica de la agrupación. Como verá más adelante, algunos dendrogramas están bien equilibrados, mientras que otros son muy caóticos.
# La entrada principal para el siguiente código es la disimilitud (matriz de distancia)
Evaluación de calidad de agrupamiento
En esta etapa, es necesario elegir entre diferentes algoritmos de agrupación y un número diferente de agrupaciones. Puede usar diferentes métodos de evaluación, sin olvidar dejarse guiar por
el sentido común . Destaqué estas palabras en negrita y cursiva, porque el significado de la elección es
muy importante : el número de grupos y el método de dividir datos en grupos debería ser práctico desde un punto de vista práctico. El número de combinaciones de valores de variables categóricas es finito (ya que son discretas), pero no será significativo ningún desglose basado en ellas. Es posible que tampoco desee tener muy pocos grupos; en este caso, serán demasiado generalizados. Al final, todo depende de su objetivo y las tareas del análisis.
En general, al crear grupos, le interesa obtener grupos de puntos de datos claramente definidos, de modo que la distancia entre dichos puntos dentro del grupo (
o compacidad ) sea mínima, y la distancia entre grupos (
separabilidad ) sea la máxima posible. Esto es fácil de entender intuitivamente: la distancia entre puntos es una medida de su disimilitud, obtenida en base a la matriz de disimilitud. Por lo tanto, la evaluación de la calidad de la agrupación se basa en la evaluación de la compacidad y la separabilidad.
A continuación, demostraré dos enfoques y mostraré que uno de ellos puede dar resultados sin sentido.
- Método de codo : comience con él si el factor más importante para su análisis es la compacidad de los grupos, es decir, la similitud dentro de los grupos.
- Método de evaluación de siluetas : el gráfico de silueta utilizado como una medida de consistencia de datos muestra qué tan cerca está cada uno de los puntos dentro de un grupo a los puntos en los grupos vecinos.
En la práctica, estos dos métodos a menudo dan resultados diferentes, lo que puede generar cierta confusión: la compactación máxima y la separación más clara se lograrán con un número diferente de grupos, por lo que el sentido común y la comprensión de lo que realmente significan sus datos jugarán un papel importante Al tomar una decisión final.
También hay una serie de métricas que puede analizar. Los agregaré directamente al código.
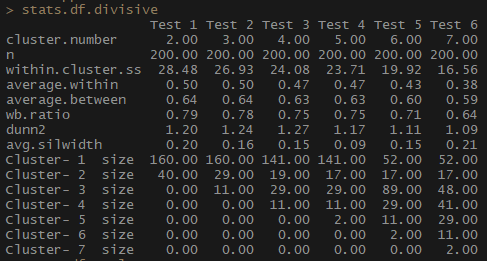
Entonces, el indicador average.within, que representa la distancia promedio entre las observaciones dentro de los grupos, disminuye, al igual que dentro de.cluster.ss (la suma de los cuadrados de las distancias entre las observaciones en un grupo). El ancho promedio de la silueta (avg.silwidth) no cambia tan inequívocamente, sin embargo, todavía se puede notar una relación inversa.
Observe cuán desproporcionados son los tamaños de clúster. No me apresuraría a trabajar con un número incomparable de observaciones dentro de los grupos. Una de las razones es que el conjunto de datos puede estar desequilibrado, y algunos grupos de observaciones superarán a todos los demás en el análisis; esto no es bueno y probablemente conducirá a errores.
stats.df.aggl <-cstats.table(gower.dist, aggl.clust.c, 7) #stats.df.aggl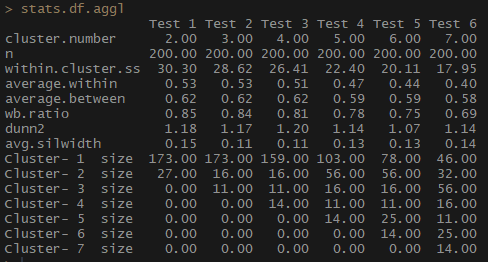
Observe cuánto mejor se equilibra el número de observaciones por grupo mediante el agrupamiento jerárquico aglomerativo basado en el método de comunicación completo.
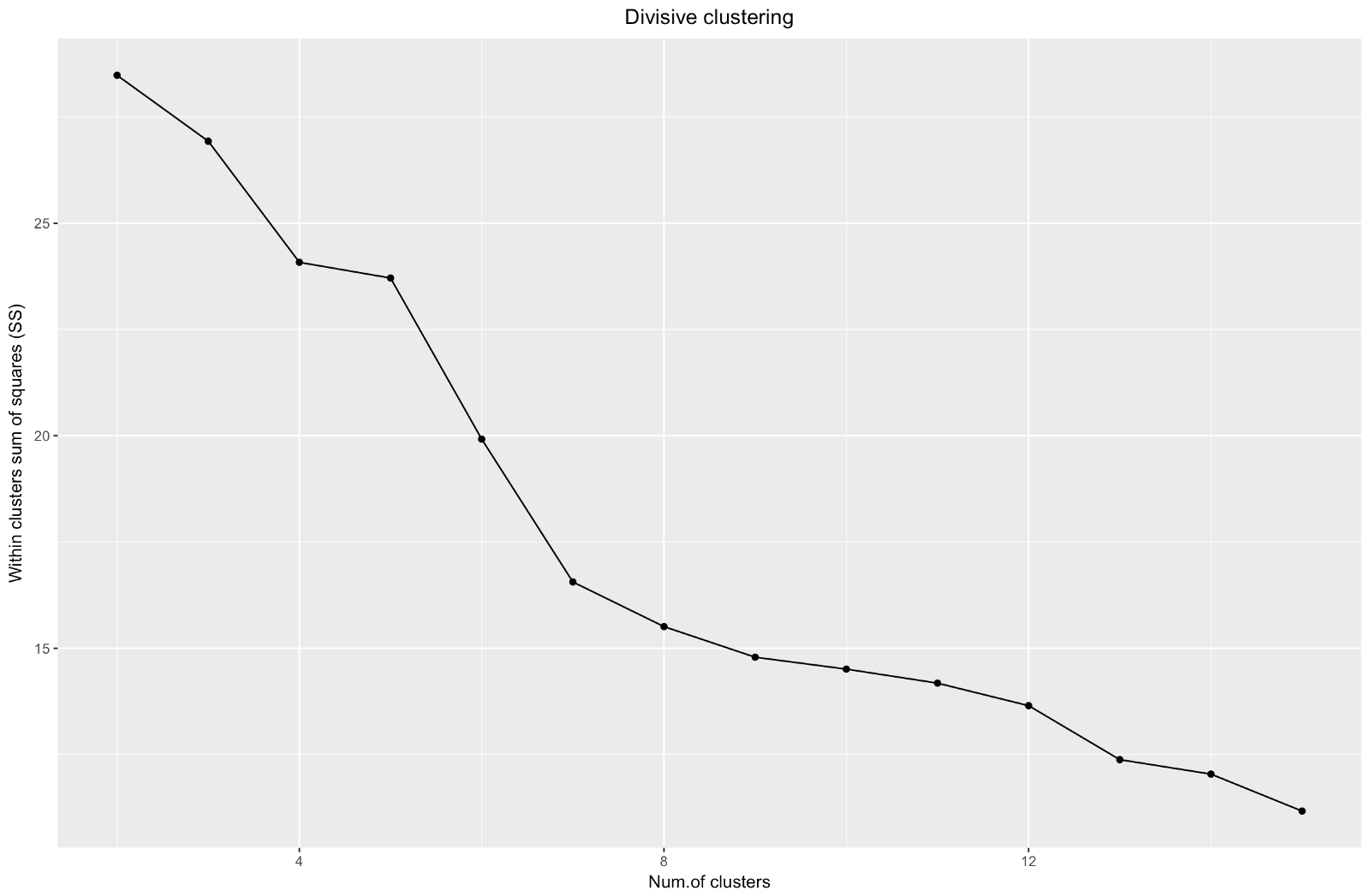
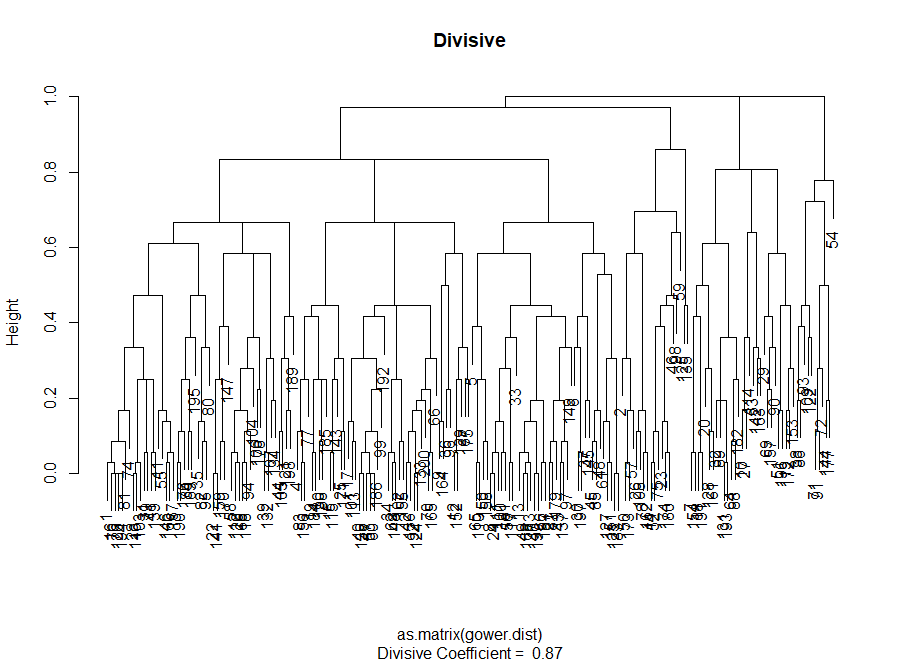
Entonces, hemos creado un gráfico del "codo". Muestra cómo la suma de las distancias al cuadrado entre las observaciones (la usamos como una medida de la proximidad de las observaciones; cuanto más pequeña es, más cercanas están las mediciones dentro del grupo) varía para un número diferente de grupos. Idealmente, deberíamos ver una "curva de codo" distinta en el punto donde la agrupación adicional solo da una ligera disminución en la suma de cuadrados (SS). Para el gráfico a continuación, me detendría en aproximadamente 7. Aunque en este caso uno de los grupos consistirá en solo dos observaciones. Veamos qué sucede durante la agrupación aglomerativa.
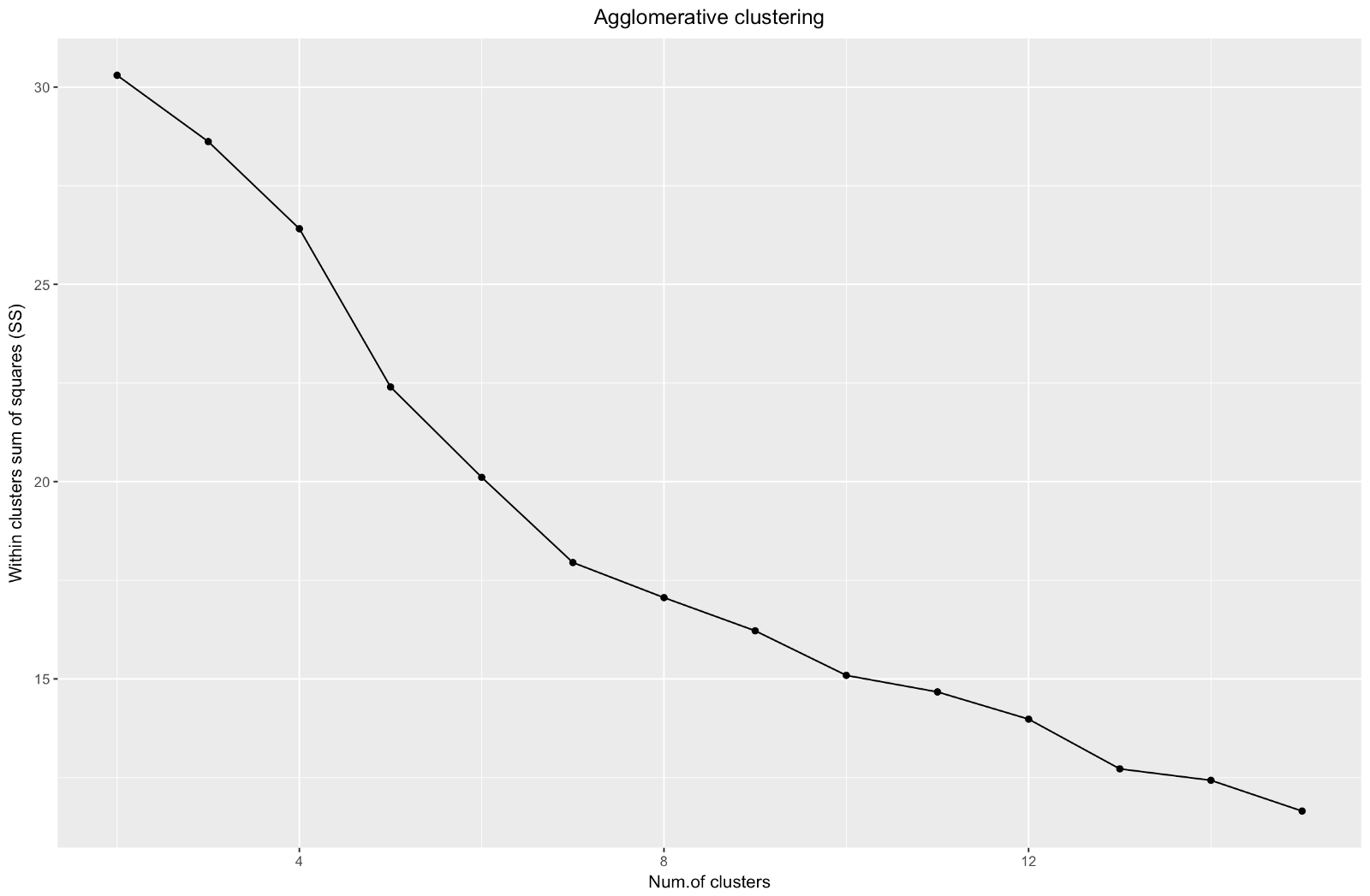
El “codo” aglomerativo es similar al divisional, pero el gráfico se ve más suave: las curvas no son tan pronunciadas. Al igual que con la agrupación divisional, me centraría en 7 agrupaciones, sin embargo, al elegir entre estos dos métodos, me gustan más los tamaños de agrupación que se obtienen mediante el método aglomerativo; es mejor que sean comparables entre sí.
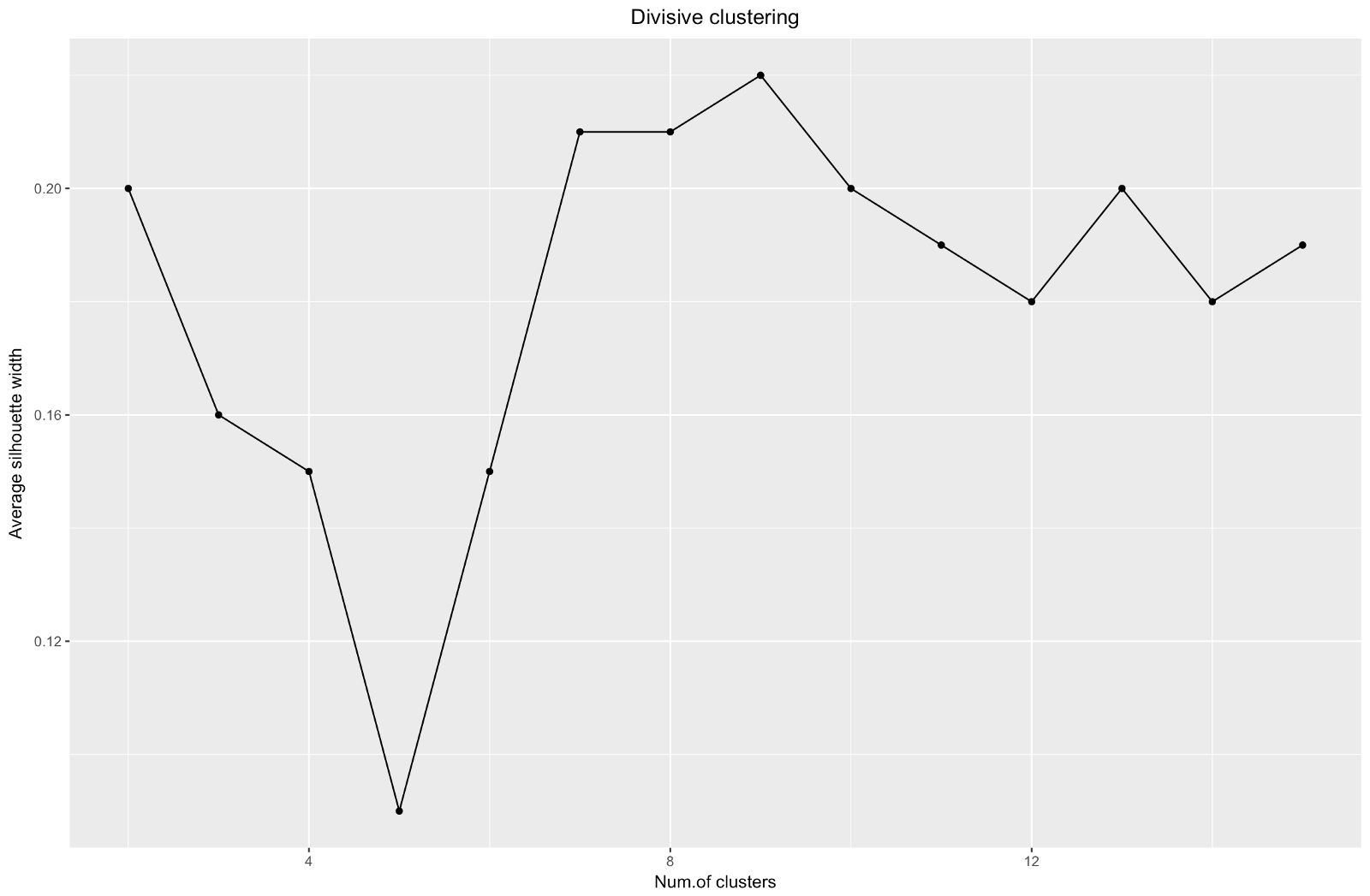
Al usar el método de estimación de silueta, debe elegir la cantidad que proporciona el coeficiente de silueta máximo, porque necesita grupos que estén lo suficientemente separados como para considerarse separados.
El coeficiente de silueta puede variar de –1 a 1, con 1 correspondiente a una buena consistencia dentro de los grupos, y –1 no muy bueno.
En el caso de la tabla anterior, elegiría 9 en lugar de 5 grupos.
A modo de comparación: en el caso "simple", el gráfico de silueta es similar al siguiente. No como el nuestro, pero casi.
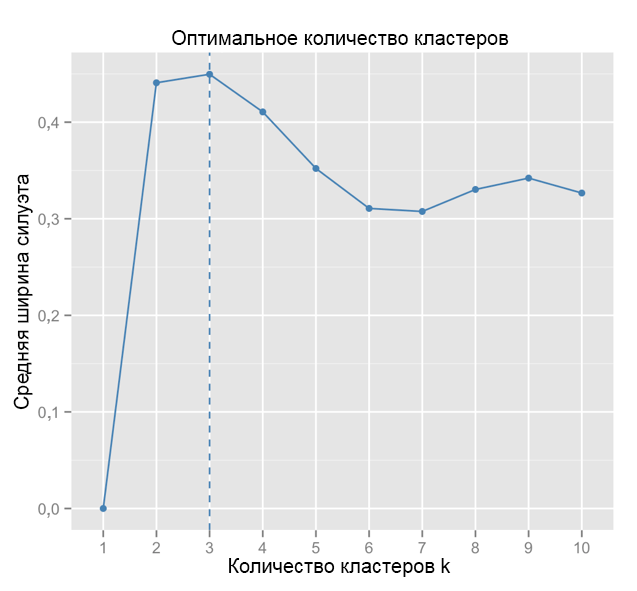Fuente: Marineros de datos ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))), aes(x=cluster.number, y=avg.silwidth)) + geom_point()+ geom_line()+ ggtitle("Agglomerative clustering") + labs(x = "Num.of clusters", y = "Average silhouette width") + theme(plot.title = element_text(hjust = 0.5))
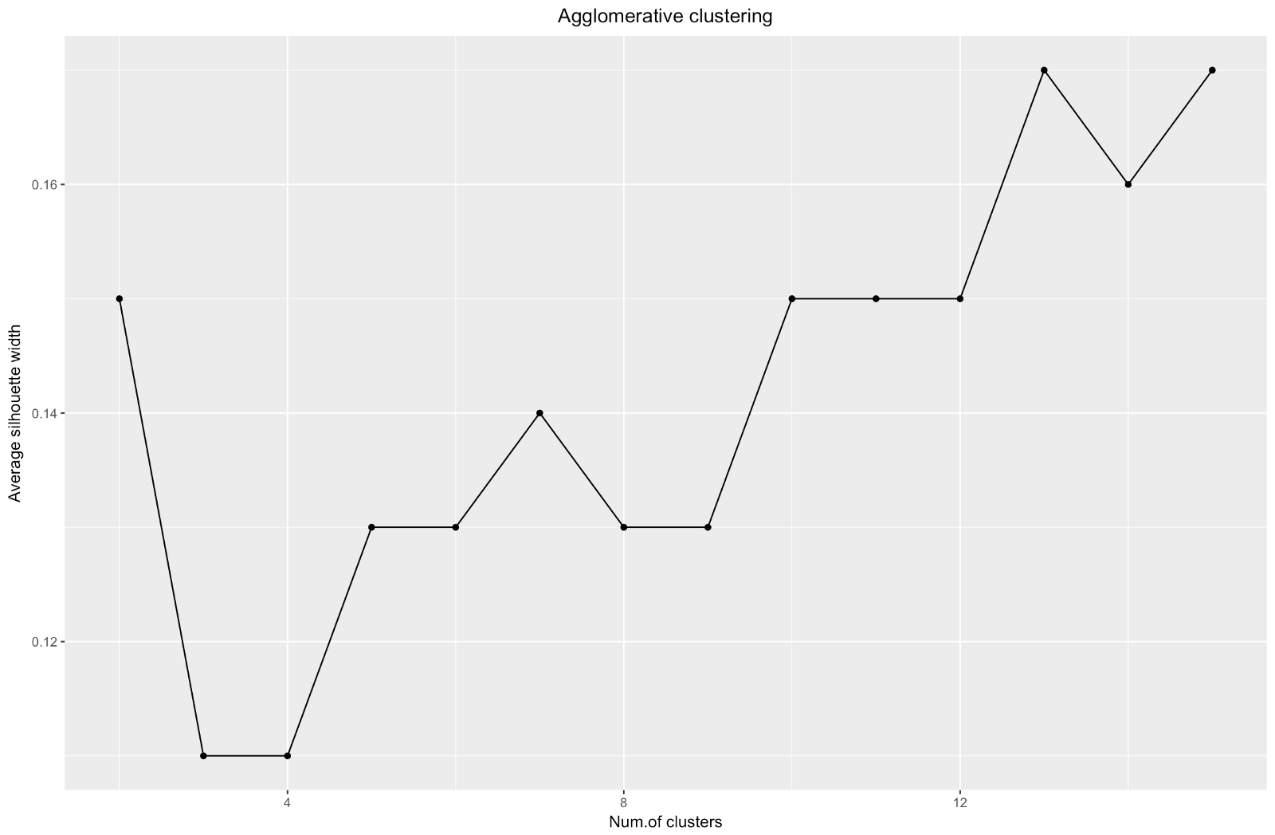
El gráfico de ancho de la silueta nos dice: cuanto más divide el conjunto de datos, más claros se vuelven los grupos. Sin embargo, al final alcanzarás puntos individuales, y no necesitas esto. Sin embargo, esto es exactamente lo que verá si comienza a aumentar el número de clústeres
k . Por ejemplo, para
k=30 obtuve el siguiente gráfico:
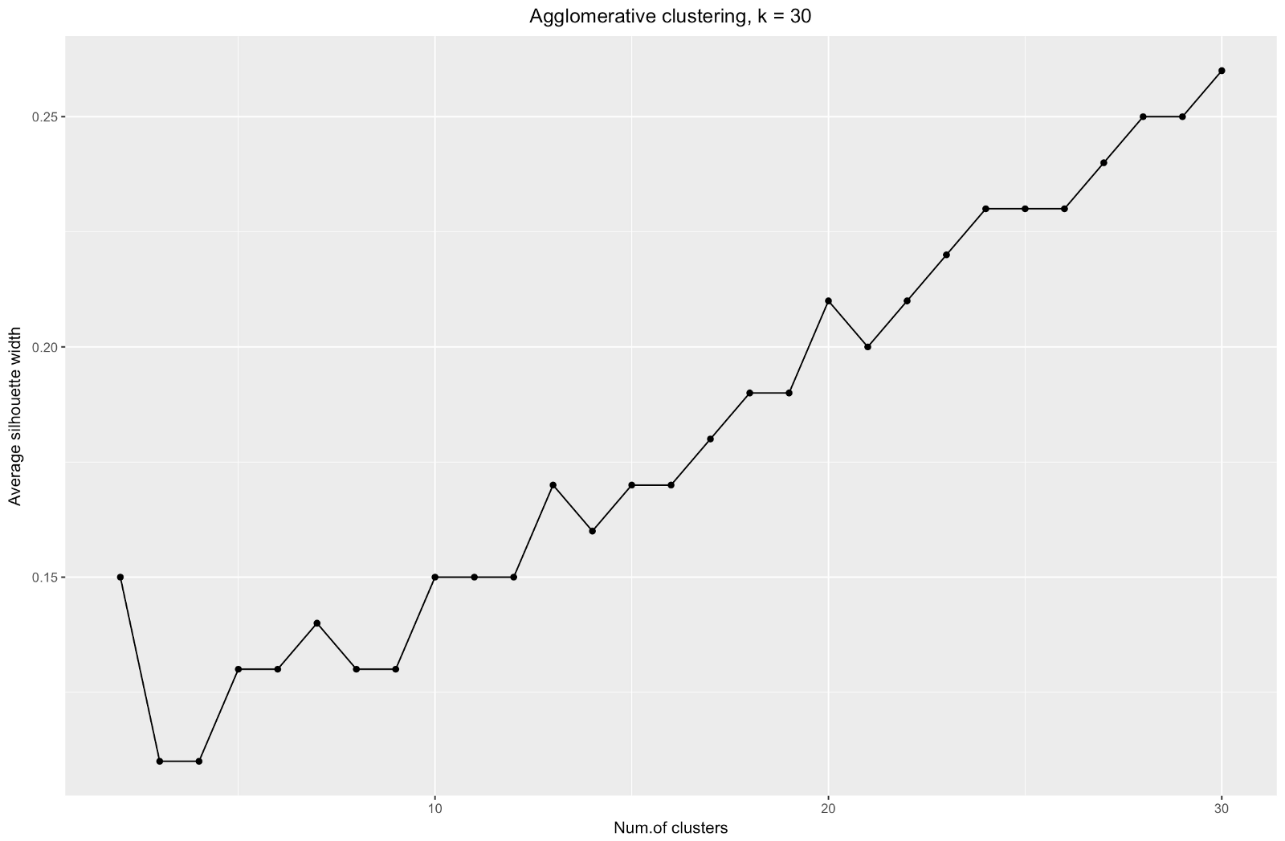
Para resumir: cuanto más divida el conjunto de datos, mejores serán los grupos, pero no podremos alcanzar puntos individuales (por ejemplo, en el gráfico anterior seleccionamos 30 grupos, y solo tenemos 200 puntos de datos).
Entonces, el agrupamiento aglomerativo en nuestro caso me parece mucho más equilibrado: los tamaños de los conglomerados son más o menos comparables (¡solo mire un conglomerado de solo dos observaciones al dividir por el método divisional!), Y me detendría en 7 conglomerados obtenidos por este método. Veamos cómo se ven y de qué están hechos.
El conjunto de datos consta de 6 variables que deben visualizarse en 2D o 3D, por lo que debe trabajar duro. La naturaleza de los datos categóricos también impone algunas limitaciones, por lo que las soluciones preparadas pueden no funcionar. Necesito: a) ver cómo se dividen las observaciones en grupos, b) entender cómo se clasifican las observaciones. Por lo tanto, creé a) un dendrograma de color, b) un mapa de calor del número de observaciones por variable dentro de cada grupo.
library("ggplot2") library("reshape2") library("purrr") library("dplyr")
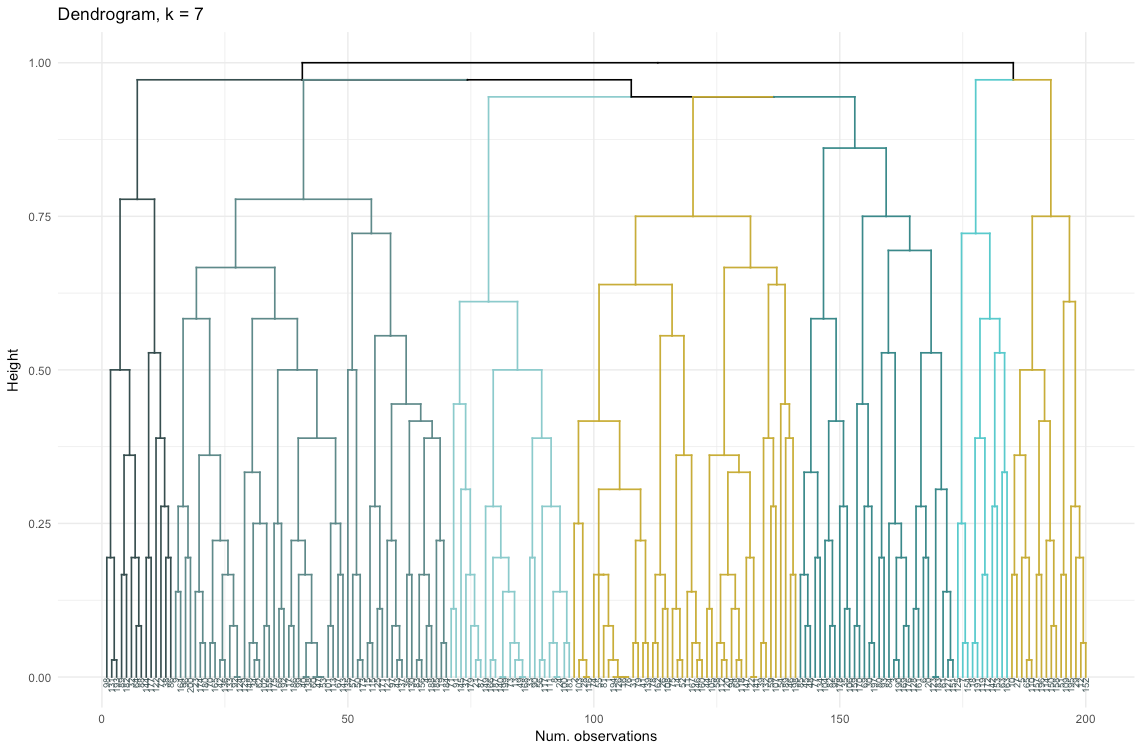
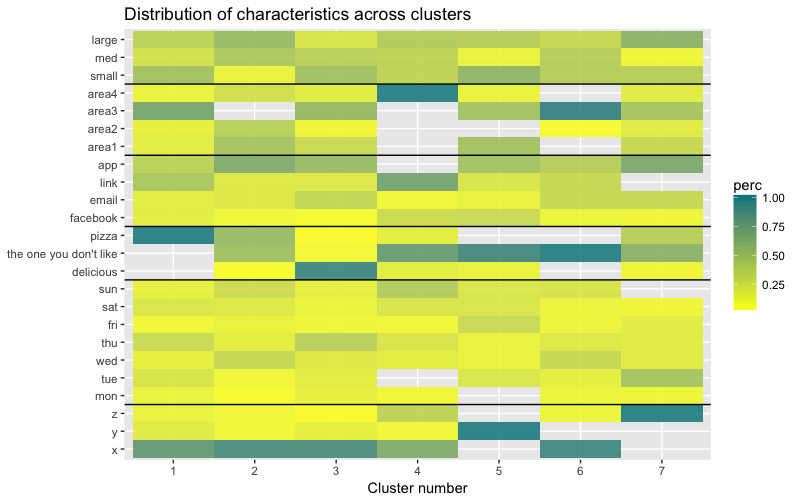
El mapa de calor muestra gráficamente cuántas observaciones se hacen para cada nivel de factor para los factores iniciales (las variables con las que comenzamos). El color azul oscuro corresponde a un número relativamente grande de observaciones dentro del grupo. Este mapa de calor también muestra que para el día de la semana (sol, sábado ...) y el tamaño de la canasta (grande, med, pequeño) el número de clientes en cada celda es casi el mismo, esto puede significar que estas categorías no son determinantes para el análisis, y Quizás no necesitan ser tomados en cuenta.
Conclusión
En este artículo, calculamos la matriz de disimilitud, probamos los métodos de aglomeración y división del agrupamiento jerárquico y nos familiarizamos con los métodos de codo y silueta para evaluar la calidad de los grupos.
La agrupación jerárquica divisional y aglomerativa es un buen comienzo para estudiar el tema, pero no se detenga allí si realmente desea dominar el análisis de agrupación. Existen muchos otros métodos y técnicas. La principal diferencia de agrupar datos numéricos es el cálculo de la matriz de disimilitud. Al evaluar la calidad de la agrupación, no todos los métodos estándar darán resultados confiables y significativos; es muy probable que el método de la silueta no sea adecuado.
Y finalmente, dado que ya ha pasado un tiempo desde que hice este ejemplo, ahora veo una serie de deficiencias en mi enfoque y me complacerá recibir cualquier comentario. Uno de los problemas importantes de mi análisis no estaba relacionado con la agrupación como tal:
mi conjunto de datos estaba desequilibrado de muchas maneras, y este momento no se tuvo en cuenta. Esto tuvo un efecto notable en la agrupación: el 70% de los clientes pertenecían a un nivel del factor de "ciudadanía", y este grupo dominó la mayoría de los grupos obtenidos, por lo que fue difícil calcular las diferencias dentro de otros niveles del factor. La próxima vez intentaré equilibrar el conjunto de datos y comparar los resultados de la agrupación. Pero más sobre eso en otra publicación.
Finalmente, si desea clonar mi código, aquí está el enlace a github:
https://github.com/khunreus/cluster-categorical¡Espero que hayas disfrutado este artículo!
Fuentes que me ayudaron:
Guía de agrupación jerárquica (preparación de datos, agrupación, visualización): este blog será interesante para quienes estén interesados en el análisis empresarial en el entorno R:
http://uc-r.imtqy.com/hc_clustering y
https: // uc-r. imtqy.com/kmeans_clusteringAgrupación:
http://www.sthda.com/english/articles/29-cluster-validation-essentials/97-cluster-validation-statistics-must-know-methods/( k-):
https://eight2late.wordpress.com/2015/07/22/a-gentle-introduction-to-cluster-analysis-using-r/denextend, :
https://cran.r-project.org/web/packages/dendextend/vignettes/introduction.html#the-set-function, :
https://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/:
https://jcoliver.imtqy.com/learn-r/008-ggplot-dendrograms-and-heatmaps.html,
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5025633/ ( GitHub:
https://github.com/khunreus/EnsCat ).