Crear un chatbot de conversación simple en python

¿Crees que es difícil escribir tu propio chatbot en Python que pueda soportar la conversación? Resultó ser muy fácil si encuentras un buen conjunto de datos. Además, esto se puede hacer incluso sin redes neuronales, aunque todavía se necesitará algo de magia matemática.

Seguiremos pequeños pasos: primero, recuerde cómo cargar datos en Python, luego aprenda a contar palabras, conecte gradualmente el álgebra lineal y el orden, y al final crearemos un bot para Telegram a partir del algoritmo de chat resultante.

Este tutorial es adecuado para aquellos que ya han tocado Python un poco, pero no están particularmente familiarizados con el aprendizaje automático. Intencionalmente no utilicé ninguna biblioteca nlp-sh para mostrar que algo que funciona puede ensamblarse en sklearn desnudo.

Busque una respuesta en el conjunto de datos de diálogo

Hace un año, me pidieron que les mostrara a los muchachos que no se habían dedicado previamente al análisis de datos alguna aplicación inspiradora de aprendizaje automático que puede construir por su cuenta. Traté de traer un robot que hablara con ellos, y realmente lo hicimos en una noche. Nos gustó el proceso y el resultado, y escribí sobre ello en mi blog . Y ahora pensaba que Habru sería interesante.

Entonces aquí vamos. Nuestra tarea es crear un algoritmo que dará una respuesta adecuada a cualquier frase. Por ejemplo, en "¿cómo estás?" responde "excelente, ¿y tú?". La forma más fácil de lograr esto es encontrar una base de datos preparada de preguntas y respuestas. Por ejemplo, tome subtítulos de una gran cantidad de películas.

Sin embargo, actuaré aún más engañosamente y tomaré los datos de la competencia Yandex.Algorithm 2018 : estos son los mismos diálogos de las películas para los que los empleados de Toloka marcaron secuelas buenas y no malas. Yandex recopiló estos datos para entrenar a Alice (artículos sobre sus entrañas 1 , 2 , 3 ). En realidad, me inspiró Alice cuando se me ocurrió este bot. La tabla de Yandex muestra las últimas tres frases y la respuesta a ellas (respuesta), pero usaremos solo la más reciente (context_0).

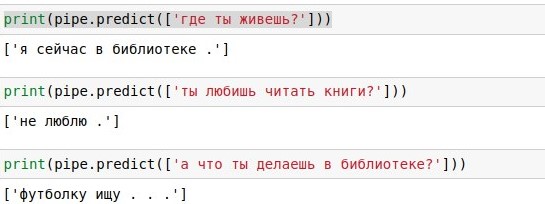
Con una base de datos de diálogos de este tipo, simplemente puede buscar en ella cada réplica del usuario y darle una respuesta inmediata (si hay muchas de esas réplicas, elija al azar). Con "¿cómo estás?" resultó genial, como lo demuestra la captura de pantalla adjunta. Esto, en todo caso, es un cuaderno jupyter en Python 3. Si desea repetir esto usted mismo, la forma más fácil es instalar Anaconda : incluye Python y un montón de paquetes útiles para ello. O no puede instalar nada, pero ejecute una computadora portátil en una nube de Google .



El problema con las búsquedas literales es que tiene una cobertura baja. A la frase "¿cómo estás?" en la base de datos de 40 mil respuestas no hubo coincidencia exacta, aunque tiene el mismo significado. Por lo tanto, en la siguiente sección, complementaremos nuestro código utilizando diferentes matemáticas para implementar una búsqueda aproximada. Y antes de eso, puede leer sobre la biblioteca de pandas y descubrir qué hace cada una de las 6 líneas del código anterior.

Vectorización de texto

Ahora estamos hablando de cómo convertir textos en vectores numéricos para realizar una búsqueda aproximada en ellos.

Ya nos hemos reunido con la biblioteca de pandas en Python: le permite cargar tablas, buscar en ellas, etc. Ahora toquemos la biblioteca scikit-learn (sklearn), que permite una manipulación de datos más complicada, lo que se llama aprendizaje automático. Esto significa que cualquier algoritmo debe mostrar primero los datos (ajuste) para que aprenda algo importante sobre ellos. Como resultado, el algoritmo "aprende" a hacer algo útil con estos datos: transformarlos (transformar) o incluso predecir valores desconocidos (predecir).

En este caso, queremos convertir textos ("preguntas") en vectores numéricos. Esto es necesario para que sea posible encontrar textos que estén "cercanos" entre sí, utilizando el concepto matemático de distancia. La distancia entre dos puntos puede calcularse mediante el teorema de Pitágoras, como la raíz de la suma de los cuadrados de las diferencias de sus coordenadas. En matemáticas, esto se llama métrica euclidiana. Si podemos convertir textos en objetos que tienen coordenadas, entonces podemos calcular la métrica euclidiana y, por ejemplo, encontrar en la base de datos una pregunta que se parezca más a "¿qué estás pensando?".

La forma más fácil de especificar las coordenadas del texto es numerar todas las palabras en el idioma y decir que la coordenada i-ésima del texto es igual al número de apariciones de la palabra i-ésima que contiene. Por ejemplo, para el texto "No puedo evitar llorar", la coordenada de la palabra "no" es 2, las coordenadas de las palabras "I", "can" y "cry" son 1, y las coordenadas de todas las otras palabras (decenas de miles de las cuales) son 0. Esta representación pierde información sobre el orden de las palabras, pero aún funciona bastante bien.

El problema es que para las palabras que se encuentran a menudo (por ejemplo, partículas “y” y “a”), las coordenadas serán desproporcionadamente grandes, aunque contengan poca información. Para mitigar este problema, la coordenada de cada palabra se puede dividir por el logaritmo del número de textos en los que aparece dicha palabra; esto se llama tf-idf y también funciona bien.



Solo hay un problema: en nuestra base de datos de 60 mil "preguntas" textuales, que contienen 14 mil palabras diferentes. Si convierte todas las preguntas en vectores, obtendrá una matriz de 60k * 14k. No es muy bueno trabajar con esto, por lo que hablaremos sobre la reducción de la dimensión más adelante.

Reducción dimensional

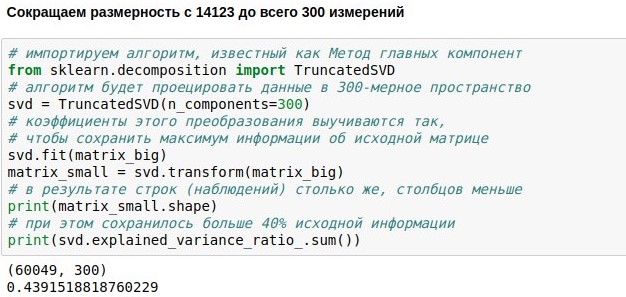
Ya hemos establecido la tarea de crear un chatbot de chat, descargar y vectorizar datos para su capacitación. Ahora tenemos una matriz numérica que representa las réplicas de los usuarios. Consta de 60 mil filas (había tantas réplicas en la base de datos de diálogos) y 14 mil columnas (había tantas palabras diferentes en ellas). Nuestra tarea ahora es hacerlo más pequeño. Por ejemplo, para presentar cada texto no como un vector de 14123 dimensiones, sino solo como un vector de 300 dimensiones.

Esto se puede lograr multiplicando nuestra matriz de tamaño 60049x14123 por una matriz de proyección especialmente seleccionada de tamaño 14123x300, al final obtenemos el resultado 60049x300. El algoritmo PCA ( método del componente principal ) selecciona la matriz de proyección para que la matriz original pueda ser reconstruida con el error estándar más pequeño. En nuestro caso, fue posible mantener aproximadamente el 44% de la matriz original, aunque la dimensión se redujo en casi 50 veces.



¿Qué hace posible una compresión tan efectiva? Recuerde que la matriz original contiene contadores para mencionar palabras individuales en los textos. Pero las palabras, como regla, se usan no independientemente entre sí, sino en contexto. Por ejemplo, cuantas más veces aparezca la palabra "bloqueo" en el texto de las noticias, más veces, lo más probable es que la palabra "telegramas" también se encuentre en este texto. Pero la correlación de la palabra "bloqueo", por ejemplo, con la palabra "caftan" es negativa: se encuentran en diferentes contextos.

Por lo tanto, resulta que el método de los componentes principales no recuerda todas las 14 mil palabras, sino 300 contextos típicos por los cuales se puede tratar de restaurar estas palabras. Las columnas de la matriz de proyección correspondientes a palabras sinónimas suelen ser similares entre sí porque estas palabras a menudo se encuentran en el mismo contexto. Esto significa que es posible reducir las mediciones redundantes sin perder la información.

En muchas aplicaciones modernas, la matriz de proyección de palabras se calcula mediante redes neuronales (por ejemplo, word2vec ). Pero, de hecho, el álgebra lineal simple ya es suficiente para un resultado prácticamente útil. El método de los componentes principales se reduce computacionalmente a SVD, y consiste en calcular los vectores propios y los valores propios de la matriz. Sin embargo, esto puede programarse sin siquiera saber los detalles.

Buscar vecinos cercanos

En las secciones anteriores, cargamos el cuadro de diálogo en Python, lo vectorizamos y redujimos la dimensión, y ahora queremos aprender finalmente cómo buscar a nuestros vecinos más cercanos en nuestro espacio de 300 dimensiones y finalmente responder preguntas significativas.

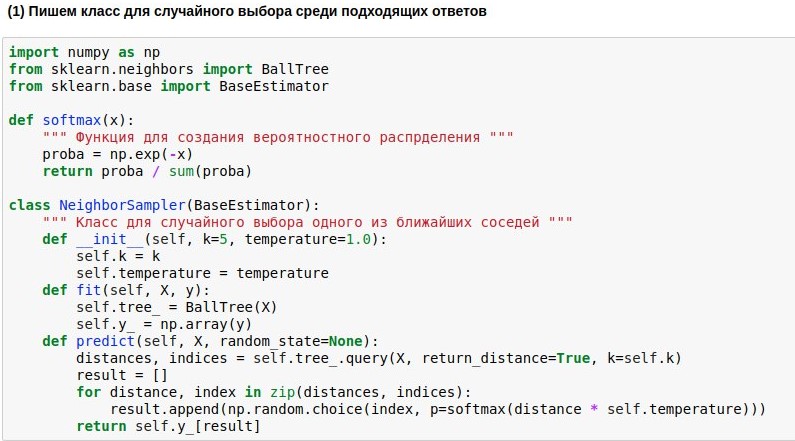
Dado que aprendimos a mapear preguntas al espacio euclidiano de dimensión no muy alta, la búsqueda de vecinos en él puede llevarse a cabo con bastante rapidez. Utilizaremos el algoritmo de búsqueda de vecinos BallTree listo para usar . Pero escribiremos nuestro modelo de envoltura, que elegiría uno de los k vecinos más cercanos, y cuanto más cerca esté el vecino, mayor será la probabilidad de su elección. Porque tomar siempre a uno de los vecinos más cercanos es aburrido, pero no estar atado a la semejanza es peligroso.

Por lo tanto, queremos convertir las distancias encontradas desde la consulta a los textos de referencia en la probabilidad de elegir estos textos. Para hacer esto, puede usar la función softmax, que a menudo todavía se encuentra a la salida de las redes neuronales. Ella convierte sus argumentos en un conjunto de números no negativos, cuya suma es 1, justo lo que necesitamos. Además, podemos usar las "probabilidades" obtenidas para una elección aleatoria de respuesta.



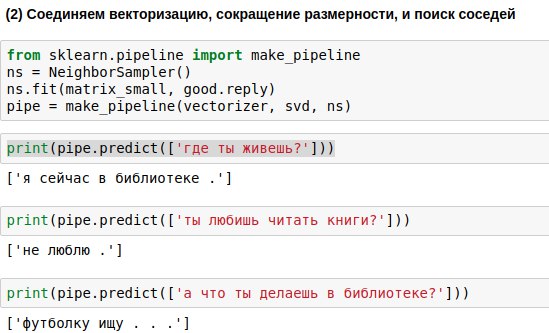
Las frases que ingresará el usuario deben pasarse por los tres algoritmos: el vectorizador, el método del componente principal y el algoritmo de selección de respuesta. Para escribir menos código, puede vincularlos en una sola cadena (canalización), aplicando los algoritmos secuencialmente.

Como resultado, obtuvimos un algoritmo que, en la pregunta de un usuario, es capaz de encontrar una pregunta similar a ella y darle una respuesta. Y a veces estas respuestas incluso suenan casi significativas.

Publicando un bot en Telegram

Ya hemos descubierto cómo hacer una sala de chat chatbot que ofrezca respuestas aproximadamente relevantes a las solicitudes de los usuarios. Ahora te estoy mostrando cómo lanzar un chatbot en Telegram.

La forma más fácil de usar esto es la API Telegram de envoltorio ya preparada para python, por ejemplo, pytelegrambotapi . Entonces, instrucciones paso a paso:

1. Registre su futuro bot con @botfather y obtenga un token de acceso, que deberá insertar en su código.
2. Ejecute el comando de instalación una vez: pip install pytelegrambotapi en la línea de comando (o mediante! Directamente en el bloc de notas).
3. Ejecute el código como en la captura de pantalla. La celda entrará en modo de ejecución (*), y mientras esté en este modo, puede comunicarse con su bot todo lo que quiera. Para detener el bot, presione Ctrl + C. La triste pero importante verdad: si se encuentra en Rusia, lo más probable es que antes de iniciar esta celda, deba encender la VPN para no obtener un error al conectarse a los telegramas. Una alternativa más simple a VPN es escribir todo el código no en su computadora local, sino en google colab ( algo como esto ).
4. Si desea que el bot funcione permanentemente, debe poner su código en algún servicio en la nube, por ejemplo, AWS, Heroku, now.sh o Yandex.Cloud. Puede obtener información sobre cómo ejecutarlos en los detalles más pequeños en los sitios de estos servicios o en artículos allí en Habré. Por ejemplo, un nabo con un pequeño ejemplo de un robot que se ejecuta en heroku y coloca registros en mongodb.

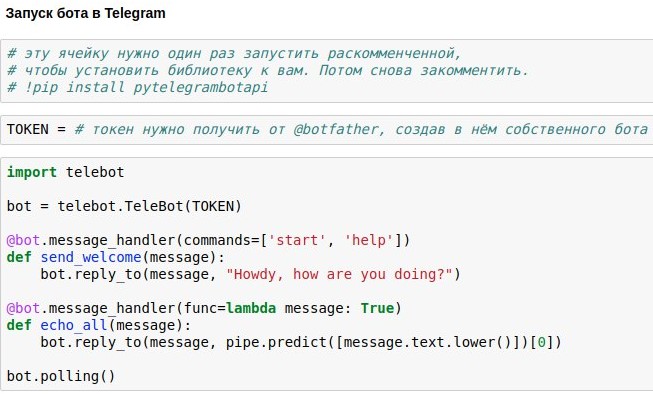
Intencionalmente no subo el código completo para el artículo: obtendrá mucho más placer y experiencia útil cuando lo imprima usted mismo y obtenga un bot de trabajo como resultado de sus propios esfuerzos. Bueno, o si eres demasiado vago para hacer esto, puedes chatear con mi versión del bot.