Redes neuronales y aprendizaje profundo, capítulo 5: ¿por qué las redes neuronales profundas son tan difíciles de entrenar?

Imagine que es ingeniero y le pidieron que desarrolle una computadora desde cero. Una vez que está sentado en la oficina, tiene dificultades para diseñar circuitos lógicos, distribuir las válvulas AND, OR, etc., y de repente su jefe entra y le cuenta las malas noticias. El cliente simplemente decidió agregar un requisito inesperado al proyecto: el esquema de toda la computadora no debe tener más de dos capas:



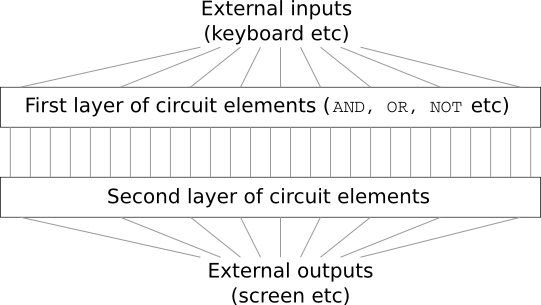
Estás sorprendido y le dices al jefe: "Sí, ¡el cliente está loco!"

El jefe responde: “Yo también lo creo. Pero el cliente debe obtener lo que quiere ".

De hecho, en un sentido estricto, el cliente no está completamente loco. Suponga que puede usar una puerta lógica especial que le permite conectar cualquier cantidad de entradas a través de AND. Y se le permite usar la compuerta NAND con cualquier cantidad de entradas, es decir, una compuerta que sume muchas entradas a través de AND, y luego invierta el resultado. Resulta que con tales válvulas especiales puede calcular cualquier función con solo un circuito de dos capas.

Sin embargo, solo porque se pueda hacer algo no significa que valga la pena hacerlo. En la práctica, al resolver problemas asociados con el diseño de circuitos lógicos (y casi todos los problemas algorítmicos), generalmente comenzamos resolviendo subtareas y luego ensamblamos gradualmente una solución completa. En otras palabras, creamos una solución a través de muchos niveles de abstracción.

Por ejemplo, supongamos que diseñamos un circuito lógico para multiplicar dos números. Es probable que queramos construirlo a partir de subcircuitos que implementan operaciones como la suma de dos números. Los subcircuitos de adición, a su vez, consistirán en subcircuitos que agreguen dos bits. En términos generales, nuestro esquema se verá así:



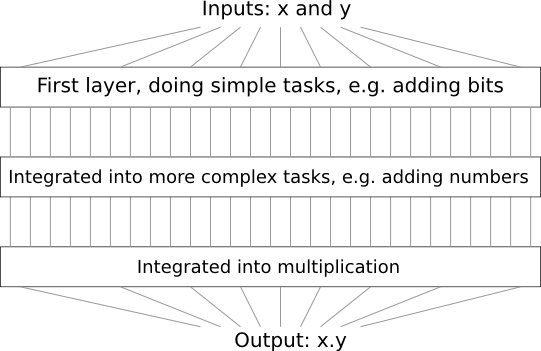
Es decir, el último circuito contiene al menos tres capas de elementos del circuito. De hecho, probablemente tendrá más de tres capas cuando separemos las subtareas en otras más pequeñas que las que describí. Pero entendiste el principio.

Por lo tanto, los esquemas profundos facilitan el proceso de diseño. Pero ayudan no solo en el diseño. Existe evidencia matemática de que para calcular algunas funciones en circuitos muy poco profundos es necesario usar un número exponencialmente mayor de elementos que en los profundos. Por ejemplo, hay una famosa serie de trabajos científicos de la década de 1980, donde se demostró que calcular la paridad de un conjunto de bits requiere un número exponencialmente mayor de puertas con un circuito poco profundo. Por otro lado, cuando se usan esquemas profundos, es más fácil calcular la paridad usando un esquema pequeño: simplemente calcula la paridad de los pares de bits, y luego usa el resultado para calcular la paridad de los pares de bits, y así sucesivamente, alcanzando rápidamente la paridad general. Por lo tanto, los esquemas profundos pueden ser mucho más poderosos que los superficiales.

Hasta ahora, este libro ha utilizado un enfoque de redes neuronales (NS), similar a las solicitudes de un cliente loco. Casi todas las redes con las que trabajamos tenían una sola capa oculta de neuronas (más las capas de entrada y salida):



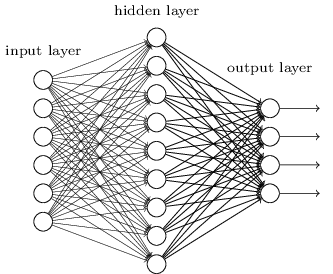
Estas redes simples resultaron ser muy útiles: en capítulos anteriores usamos tales redes para clasificar números escritos a mano con una precisión superior al 98%. Sin embargo, es intuitivamente claro que las redes con muchas capas ocultas serán mucho más potentes:



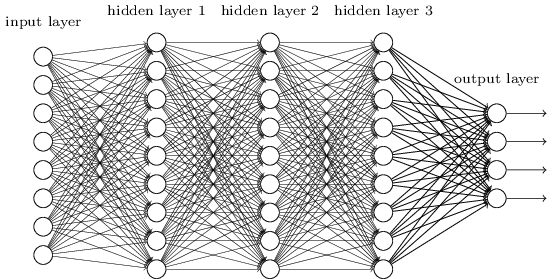
Dichas redes pueden usar capas intermedias para crear muchos niveles de abstracción, como es el caso de nuestros esquemas booleanos. Por ejemplo, en el caso del reconocimiento de patrones, las neuronas de la primera capa pueden aprender a reconocer caras, neuronas de la segunda capa, formas más complejas, por ejemplo, triángulos o rectángulos creados a partir de caras. Entonces, la tercera capa podrá reconocer formas aún más complejas. Y así sucesivamente. Es probable que estas muchas capas de abstracción otorguen a las redes profundas una ventaja convincente para resolver problemas de reconocimiento de patrones complejos. Además, como en el caso de los circuitos, hay resultados teóricos que confirman que las redes profundas tienen inherentemente más capacidades que las superficiales.

¿Cómo entrenamos estas redes neuronales profundas (GNS)? En este capítulo, trataremos de entrenar STS usando nuestro caballo de batalla entre los algoritmos de entrenamiento: descenso de propagación hacia atrás en gradiente estocástico. Sin embargo, encontraremos un problema: nuestro STS no funcionará mucho mejor (si es que se supera) que los superficiales.

Este fracaso parece extraño a la luz de la discusión anterior. Pero en lugar de renunciar al STS, profundizaremos en el problema e intentaremos entender por qué el STS es difícil de entrenar. Cuando analicemos más de cerca el problema, encontraremos que diferentes capas en el STS aprenden a velocidades muy diferentes. En particular, cuando las últimas capas de la red se entrenan bien, las primeras a menudo se atascan durante el entrenamiento y no aprenden casi nada. Y no es solo mala suerte. Encontraremos razones fundamentales para ralentizar el aprendizaje que están relacionadas con el uso de técnicas de aprendizaje basadas en gradientes.

Profundizando en este problema, descubrimos que también puede ocurrir el fenómeno opuesto: las primeras capas pueden aprender bien y las posteriores se atascan. De hecho, descubriremos la inestabilidad interna asociada con el entrenamiento de descenso de gradiente en NS multicapa profunda. Y debido a esta inestabilidad, las capas tempranas o tardías a menudo se atascan en el entrenamiento.

Todo esto suena bastante desagradable. Pero sumidos en estas dificultades, podemos comenzar a desarrollar ideas sobre lo que se debe hacer para una capacitación efectiva de STS. Por lo tanto, estos estudios serán una buena preparación para el próximo capítulo, donde utilizaremos el aprendizaje profundo para abordar los problemas del reconocimiento de imágenes.

Problema de gradiente de desvanecimiento

Entonces, ¿qué sale mal cuando intentamos entrenar una red profunda?

Para responder a esta pregunta, volvemos a la red que contiene solo una capa oculta. Como de costumbre, usaremos el problema de clasificación de dígitos MNIST como una caja de arena para aprender y experimentar.

Si desea repetir todos estos pasos en su computadora, debe tener Python 2.7 instalado, la biblioteca Numpy y una copia del código que se puede tomar del repositorio:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git 

Puede prescindir de git simplemente descargando los datos y el código . Vaya al subdirectorio src y desde el shell de python cargue los datos MNIST:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Configure la red:

 >>> import network2 >>> net = network2.Network([784, 30, 10]) 

Dicha red tiene 784 neuronas en la capa de entrada, que corresponde a 28 × 28 = 784 píxeles de la imagen de entrada. Utilizamos 30 neuronas ocultas y 10 salidas, correspondientes a diez posibles opciones de clasificación para los números MNIST ('0', '1', '2', ..., '9').

Intentemos entrenar nuestra red durante 30 épocas enteras usando mini paquetes de 10 ejemplos de entrenamiento a la vez, velocidad de aprendizaje η = 0.1 y parámetro de regularización λ = 5.0. Durante el entrenamiento, rastrearemos la precisión de la clasificación a través de validation_data:

 >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Obtenemos una precisión de clasificación de 96.48% (más o menos, los números variarán con diferentes lanzamientos), comparable a nuestros resultados anteriores con configuraciones similares.

Agreguemos otra capa oculta, que también contiene 30 neuronas, e intentemos entrenar la red con los mismos hiperparámetros:

 >>> net = network2.Network([784, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

La precisión de clasificación mejora a 96.90%. Es inspirador: un ligero aumento en la profundidad ayuda. Agreguemos otra capa oculta de 30 neuronas:

 >>> net = network2.Network([784, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

No sirvió de nada. El resultado incluso cayó al 96.57%, un valor cercano a la red superficial original. Y si agregamos otra capa oculta:

 >>> net = network2.Network([784, 30, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Entonces la precisión de la clasificación volverá a caer, ya a 96.53%. Estadísticamente, esta caída es probablemente insignificante, pero no tiene nada de bueno.

Este comportamiento parece extraño. Parece intuitivamente que capas ocultas adicionales deberían ayudar a la red a aprender funciones de clasificación más complejas y hacer frente mejor a la tarea. Por supuesto, el resultado no debería empeorar, porque en el peor de los casos, las capas adicionales simplemente no harán nada. Sin embargo, esto no sucede.

Entonces, ¿qué está pasando? Supongamos que las capas ocultas adicionales pueden ayudar en principio, y que el problema es que nuestro algoritmo de entrenamiento no encuentra los valores correctos para los pesos y las compensaciones. Nos gustaría entender qué está mal con nuestro algoritmo y cómo mejorarlo.

Para entender qué salió mal, visualicemos el proceso de aprendizaje en red. A continuación, construí una parte de la red [784,30,30,10], en la que hay dos capas ocultas, cada una de las cuales tiene 30 neuronas ocultas. En el diagrama, cada neurona tiene una barra que indica la tasa de cambio en el proceso de aprendizaje de la red. Una barra grande significa que los pesos y los desplazamientos de la neurona cambian rápidamente, y una pequeña significa que cambian lentamente. Más precisamente, la barra denota el gradiente ∂C / ∂b de la neurona, es decir, la tasa de cambio de costo con respecto al desplazamiento. En el capítulo 2, vimos que este valor de gradiente controla no solo la tasa de cambio de desplazamiento durante el entrenamiento, sino también la tasa de cambio de los pesos de las neuronas de entrada. No se preocupe si no puede recordar estos detalles: solo debe tener en cuenta que estas barras indican qué tan rápido cambian los pesos y los desplazamientos de las neuronas durante el entrenamiento de la red.

Para simplificar el diagrama, dibujé solo seis neuronas superiores en dos capas ocultas. Bajé las neuronas entrantes porque no tienen pesos ni sesgos. También omití las neuronas de salida, ya que estamos comparando dos capas, y tiene sentido comparar capas con la misma cantidad de neuronas. El diagrama se creó utilizando el programa generate_gradient.py al comienzo de la capacitación, es decir, inmediatamente después de que se inicializó la red.



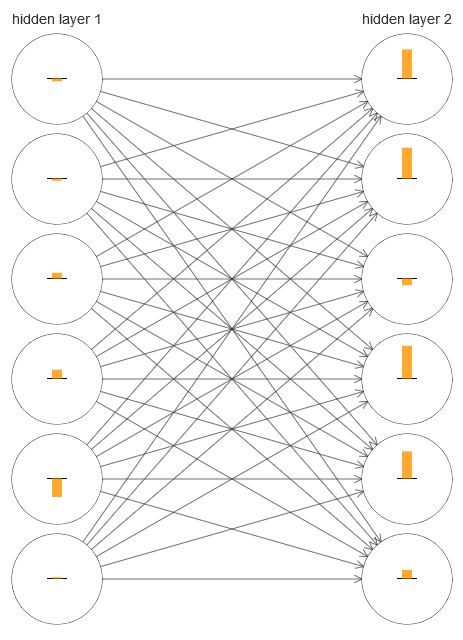
La red se inició por casualidad, por lo que esta diversidad en la velocidad de entrenamiento de las neuronas no es sorprendente. Sin embargo, inmediatamente llama la atención que en la segunda capa oculta, las tiras son básicamente mucho más que en la primera. Como resultado, las neuronas en la segunda capa aprenderán mucho más rápido que en la primera. ¿Es una coincidencia, o es probable que las neuronas en la segunda capa aprendan en general más rápido que las neuronas en la primera?

Para saber exactamente, será bueno tener una forma general de comparar la velocidad de aprendizaje en la primera y segunda capas ocultas. Para hacer esto, denotemos el gradiente como δ ^l _j = ∂C / ∂b ^l _j , es decir, como el gradiente de la neurona No. j en la capa No. l. En el segundo capítulo, lo llamamos un "error", pero aquí lo llamaré informalmente un "gradiente". Informalmente, dado que este valor no incluye explícitamente derivadas parciales del costo en peso, ∂C / ∂w. El gradiente δ ¹ puede considerarse como un vector cuyos elementos determinan qué tan rápido aprende la primera capa oculta, y δ ² como un vector cuyos elementos determinan qué tan rápido aprende la segunda capa oculta. Utilizamos las longitudes de estos vectores como estimaciones aproximadas de la velocidad de aprendizaje de las capas. Es decir, por ejemplo, la longitud || δ ¹ || mide la velocidad de aprendizaje de la primera capa oculta y la longitud || δ ² || mide la velocidad de aprendizaje de la segunda capa oculta.

Con tales definiciones y la misma configuración que arriba, encontramos que || δ ¹ || = 0.07, y || δ ² || = 0,31. Esto confirma nuestras sospechas: las neuronas en la segunda capa oculta aprenden mucho más rápido que las neuronas en la primera capa oculta.

¿Qué sucede si agregamos más capas ocultas? Con tres capas ocultas en la red [784,30,30,30,10], las velocidades de aprendizaje correspondientes serán 0.012, 0.060 y 0.283. Nuevamente, las primeras capas ocultas aprenden mucho más lentamente que la última. Agrega otra capa oculta con 30 neuronas. En este caso, las velocidades de aprendizaje correspondientes serán 0.003, 0.017, 0.070 y 0.285. El patrón se conserva: las primeras capas aprenden más lentamente que las posteriores.

Estudiamos la velocidad de aprendizaje desde el principio, justo después de que se inicializó la red. ¿Cómo cambia esta velocidad a medida que aprende? Volvamos a mirar la red con dos capas ocultas. La velocidad de aprendizaje cambia así:



Para obtener estos resultados, utilicé el descenso de gradiente por lotes con 1000 imágenes de entrenamiento y entrenamiento para 500 eras. Esto es ligeramente diferente de nuestros procedimientos habituales: no utilicé mini paquetes y tomé solo 1000 imágenes de entrenamiento, en lugar de un conjunto completo de 50,000 piezas. No estoy tratando de engañarte y engañarte, pero resulta que usar el descenso de gradiente estocástico con mini paquetes trae mucho más ruido a los resultados (pero si promedias el ruido, los resultados son similares). Usando los parámetros que he elegido, es fácil suavizar los resultados para que podamos ver lo que está sucediendo.

En cualquier caso, como vemos, dos capas comienzan a entrenar a dos velocidades muy diferentes (que ya sabemos). Luego, la velocidad de ambas capas cae muy rápidamente, después de lo cual se produce un rebote. Sin embargo, todo este tiempo, la primera capa oculta aprende mucho más lentamente que la segunda.

¿Qué pasa con las redes más complejas? Estos son los resultados de un experimento similar, pero con una red con tres capas ocultas [784,30,30,30,10]:



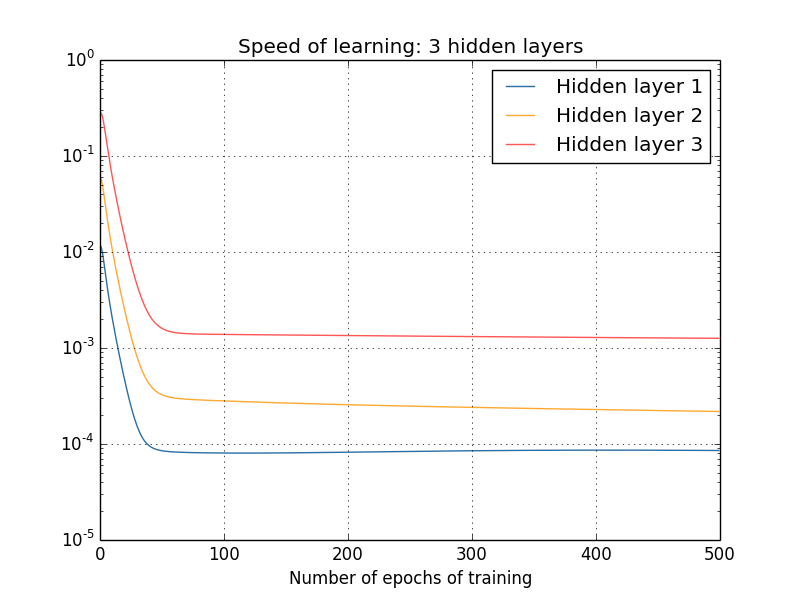
Y de nuevo, las primeras capas ocultas aprenden mucho más lentamente que la última. Finalmente, intentemos agregar una cuarta capa oculta (red [784,30,30,30,30,10]) y veamos qué sucede cuando se entrena:



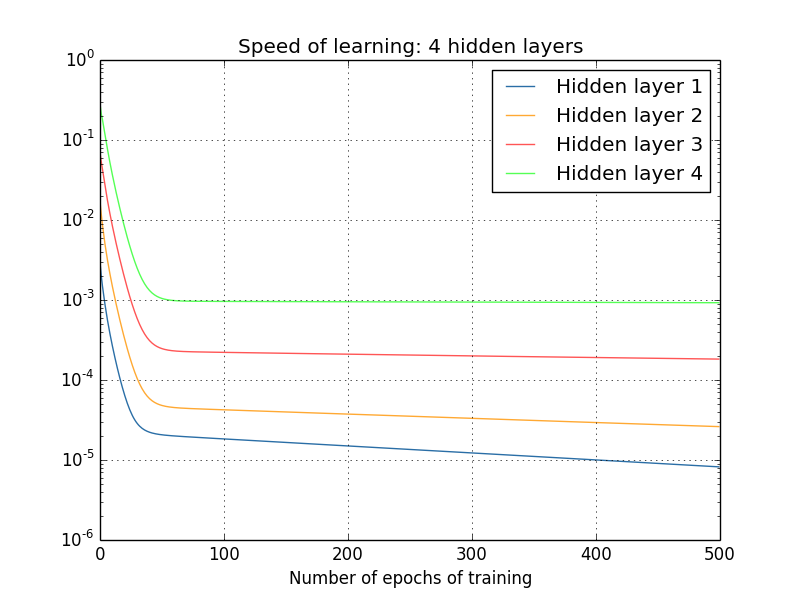
Y de nuevo, las primeras capas ocultas aprenden mucho más lentamente que la última. En este caso, la primera capa oculta aprende aproximadamente 100 veces más lento que la última. ¡No es de extrañar que hayamos tenido tantos problemas para aprender estas redes!

Hicimos una observación importante: al menos en algunos GNS, el gradiente disminuye cuando se mueve en la dirección opuesta a lo largo de capas ocultas. Es decir, las neuronas en las primeras capas se entrenan mucho más lentamente que las neuronas en la última. Y aunque observamos este efecto en una sola red, existen razones fundamentales por las que esto sucede en muchos NS. Este fenómeno se conoce como el "problema de gradiente de fuga" (ver obras 1 , 2 ).

¿Por qué hay un problema de gradiente de desvanecimiento? ¿Hay alguna forma de evitarlo? ¿Cómo lidiamos con eso cuando entrenamos STS? De hecho, pronto descubriremos que no es inevitable, aunque la alternativa no le parece muy atractiva: ¡a veces en las primeras capas el gradiente es mucho más grande! Esto ya es un problema de crecimiento de gradiente explosivo, y no es más bueno en él que en el problema de un gradiente que desaparece. En general, resulta que el gradiente en el STS es inestable y es propenso a un crecimiento explosivo o desaparecer en las primeras capas. Esta inestabilidad es un problema fundamental para el entrenamiento de gradiente GNS. Esto es lo que necesitamos entender, y posiblemente resolverlo de alguna manera.

Una de las reacciones a un gradiente de desvanecimiento (o inestable) es pensar si esto es realmente un problema grave. Vamos a distraernos brevemente del NS e imaginar que estamos tratando de minimizar numéricamente la función f (x) de una variable. ¿No sería bueno si la derivada f ′ (x) fuera pequeña? ¿No significa esto que ya estamos cerca del extremo? Y de la misma manera, ¿un pequeño gradiente en las primeras capas del GNS no significa que ya no necesitamos ajustar mucho los pesos y los desplazamientos?

Por supuesto que no. Recuerde que inicializamos aleatoriamente los pesos y las compensaciones de la red. Es muy poco probable que nuestros pesos y mezclas originales funcionen bien con lo que queremos de nuestra red. Como ejemplo específico, considere la primera capa de pesos en la red [784,30,30,30,10], que clasifica los números MNIST. La inicialización aleatoria significa que la primera capa expulsa la mayor parte de la información sobre la imagen entrante. Incluso si las capas posteriores se entrenaran cuidadosamente, sería extremadamente difícil para ellos determinar el mensaje entrante, simplemente debido a la falta de información. Por lo tanto, es absolutamente imposible imaginar que la primera capa simplemente no necesita entrenamiento. Si vamos a entrenar STS, debemos entender cómo resolver el problema de un gradiente que desaparece.

¿Qué causa el problema del gradiente de desvanecimiento? Gradientes inestables en GNS

Para comprender cómo aparece el problema de un gradiente de fuga, considere el NS más simple: con solo una neurona en cada capa. Aquí hay una red con tres capas ocultas:



Aquí w ₁ , w ₂ , ... son pesos, b ₁ , b ₂ , ... son desplazamientos, C es una función de costo determinada. Solo como recordatorio, diré que la salida a _j de la neurona No. j es igual a σ (z _j ), donde σ es la función de activación sigmoidea habitual, y z _j = w _j a _{j - 1} + b _j es la entrada ponderada de la neurona. Describí la función de costo al final para enfatizar que el costo es una función de la salida de la red, y ₄ : si la salida real está cerca de lo que desea, entonces el costo será pequeño y, si está lejos, será grande.

Estudiamos el gradiente ∂C / ∂b ₁ asociado con la primera neurona oculta. Encontramos la expresión para ∂C / ∂b ₁ y, habiéndola estudiado, entenderemos por qué surge el problema del gradiente de fuga.

Comenzamos demostrando la expresión para ∂C / ∂b ₁ . Parece inexpugnable, pero en realidad su estructura es simple, y lo describiré pronto. Aquí está esta expresión (por ahora, ignore la red misma y observe que σ es solo una derivada de la función σ):



La estructura de la expresión es la siguiente: para cada neurona en la red hay un término de multiplicación σ ′ (z _j ), para cada peso hay w _j , y también está el último término, ∂C / ∂a ₄ , correspondiente a la función de costo. Tenga en cuenta que coloqué los miembros correspondientes sobre las partes correspondientes de la red. Por lo tanto, la red en sí es una regla mnemónica para la expresión.

Puede tomar esta expresión con fe y saltar su discusión directamente al lugar donde se explica cómo se relaciona con el problema del gradiente de desvanecimiento. No hay nada de malo en esto, ya que esta expresión es un caso especial de nuestra discusión sobre la propagación hacia atrás. Sin embargo, es fácil explicar su fidelidad, por lo que será bastante interesante (y quizás instructivo) que estudies esta explicación.

Imagine que hicimos un pequeño cambio en Δb ₁ al desplazamiento b ₁ . Esto enviará una serie de cambios en cascada en el resto de la red. Primero, esto hará que cambie la salida de la primera neurona oculta Δa ₁ . Esto, a su vez, fuerza a Δz ₂ a cambiar en la entrada ponderada a la segunda neurona oculta. Entonces habrá un cambio en Δa ₂ en la salida de la segunda neurona oculta. Y así sucesivamente, hasta un cambio en ΔC en el valor de salida. Resulta que:

$$

$$\ frac {\ partial C} {\ partial b_1} \ approx \ frac {\ Delta C} {\ Delta b_1} \ tag {114}$$

Esto sugiere que podemos derivar una expresión para el gradiente ∂C / ∂b ₁ , monitoreando cuidadosamente la influencia de cada paso en esta cascada.

Para hacer esto, pensemos cómo Δb ₁ hace que la salida a _{1 de la} primera neurona oculta cambie. Tenemos a ₁ = σ (z ₁ ) = σ (w ₁ a ₀ + b ₁ ), por lo tanto

$$

$$\ Delta a_1 \ approx \ frac {\ partial \ sigma (w_1 a_0 + b_1)} {\ partial b_1} \ Delta b_1 \ tag {115}$$

$$

$$= \ sigma '(z_1) \ Delta b_1 \ tag {116}$$

El término σ ′ (z ₁ ) debería parecer familiar: este es el primer término de nuestra expresión para el gradiente ∂C / ∂b ₁ . Intuitivamente, convierte el cambio en el desplazamiento Δb ₁ en el cambio Δa _{1 de la} activación de salida. El cambio en Δa ₁ a su vez provoca un cambio en la entrada ponderada z ₂ = w ₂ a ₁ + b _{2 de la} segunda neurona oculta:

$$

$$\ Delta z_2 \ approx \ frac {\ partial z_2} {\ partial a_1} \ Delta a_1 \ tag {117}$$

$$

$$= w_2 \ Delta a_1 \ tag {118}$$

Combinando las expresiones para Δz ₂ y Δa ₁ , vemos cómo el cambio en el sesgo b _{1 se} propaga a lo largo de la red y afecta a z ₂ :

$$

$$\ Delta z_2 \ approx \ sigma '(z_1) w_2 \ Delta b_1 \ tag {119}$$

Y esto también debería ser familiar: estos son los dos primeros términos en nuestra expresión establecida para el gradiente ∂C / ∂b ₁ .

Esto puede continuar más allá al monitorear cómo se propagan los cambios en el resto de la red. En cada neurona seleccionamos el término σ ′ (z _j ), y a través de cada peso seleccionamos el término w _j . Como resultado, se obtiene una expresión que relaciona el cambio final ΔC de la función de costo con el cambio inicial Δb _{1 del} sesgo:

$$

$$\ Delta C \ approx \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ partial C} {\ partial a_4} \ Delta b_1 \ tag {120}$$

Dividiéndolo por Δb ₁ , realmente obtenemos la expresión deseada para el gradiente:

$$

$$\ frac {\ partial C} {\ partial b_1} = \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ partial C} {\ partial a_4} \ tag { 121}$$

¿Por qué hay un problema de gradiente de desvanecimiento?

Para entender por qué surge el problema de gradiente que desaparece, escribamos en detalle toda nuestra expresión para el gradiente:

$$

$$\ frac {\ partial C} {\ partial b_1} = \ sigma '(z_1) \ w_2 \ sigma' (z_2) \ w_3 \ sigma '(z_3) \, w_4 \ sigma' (z_4) \ \ frac {\ parcial C} {\ parcial a_4} \ tag {122}$$

Además del último término, esta expresión es el producto de términos de la forma w _j σ ′ (z _j ). Para entender cómo se comporta cada uno de ellos, observamos la gráfica de la función σ:



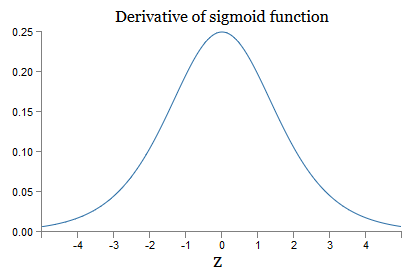
El gráfico alcanza un máximo en el punto σ ′ (0) = 1/4. Si usamos el enfoque estándar para inicializar los pesos de la red, entonces seleccionamos los pesos usando la distribución gaussiana, es decir, la raíz cuadrática media cero y la desviación estándar 1. Por lo tanto, generalmente los pesos satisfarán la desigualdad | w _j | <1. Comparando todas estas observaciones, vemos que los términos w _j σ ′ (z _j ) generalmente satisfarán la desigualdad | w _j σ ′ (z _j ) | <1/4. Y si tomamos el producto del conjunto de tales términos, entonces disminuirá exponencialmente: cuantos más términos, menor será el producto. Comienza a parecer una posible solución al problema del gradiente que desaparece.

Para escribir esto con mayor precisión, comparamos la expresión para ∂C / ∂b ₁ con la expresión del gradiente con respecto al siguiente desplazamiento, por ejemplo, ∂C / ∂b ₃ . Por supuesto, no escribimos una expresión detallada para ∂C / ∂b ₃ , pero sigue las mismas leyes descritas anteriormente para ∂C / ∂b ₁ . Y aquí hay una comparación de dos expresiones:



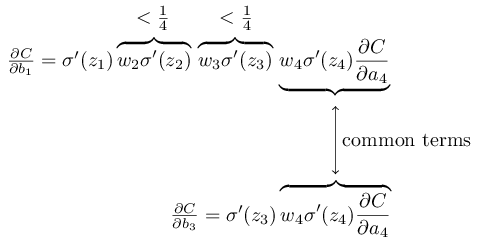
Tienen varios miembros comunes. Sin embargo, el gradiente ∂C / ∂b ₁ incluye dos términos adicionales, cada uno de los cuales tiene la forma w _j σ ′ (z _j ). Como hemos visto, tales términos generalmente no exceden 1/4. Por lo tanto, el gradiente ∂C / ∂b ₁ generalmente será 16 (o más) veces menor que ∂C / ∂b ₃ . Y esta es la causa principal del problema de gradiente que desaparece.

Por supuesto, esto no es exacto, sino una prueba informal del problema. Hay varias advertencias. En particular, uno puede estar interesado en saber si los pesos w _j aumentarán durante el entrenamiento. Si esto sucede, los términos w _j σ ′ (z _j ) en el producto ya no satisfarán la desigualdad | w _j σ ′ (z _j ) | <1/4. Y si resultan ser lo suficientemente grandes, más de 1, entonces ya no tendremos el problema de un gradiente de desvanecimiento. En cambio, el gradiente crecerá exponencialmente a medida que retrocede a través de las capas. Y en lugar del problema de gradiente que desaparece, tenemos el problema del crecimiento de gradiente explosivo.

El problema del crecimiento explosivo del gradiente

Veamos un ejemplo específico de un gradiente explosivo. El ejemplo será algo artificial: ajustaré los parámetros de la red para garantizar la aparición de un crecimiento explosivo. Pero aunque el ejemplo es artificial, su ventaja es que demuestra claramente que el crecimiento explosivo del gradiente no es una posibilidad hipotética, pero realmente puede suceder.

Para un crecimiento de gradiente explosivo, debe tomar dos pasos. Primero, elegimos grandes pesos en toda la red, por ejemplo, w1 = w2 = w3 = w4 = 100. Luego elegimos tales cambios para que los términos σ ′ (z _j ) no sean demasiado pequeños. Y esto es bastante fácil de hacer: solo necesitamos seleccionar tales desplazamientos para que la entrada ponderada de cada neurona sea zj = 0 (y luego σ ′ (z _j ) = 1/4). Por lo tanto, por ejemplo, necesitamos z ₁ = w ₁ a ₀ + b ₁ = 0. Esto se puede lograr estableciendo b ₁ = −100 ∗ a ₀ . La misma idea se puede utilizar para seleccionar otras compensaciones. Como resultado, veremos que todos los términos w _j σ ′ (z _j ) resultan ser iguales a 100 ∗ 14 = 25. Y luego obtenemos un crecimiento gradiente explosivo.

Problema de gradiente inestable

El problema fundamental no es el problema del gradiente que desaparece o el crecimiento explosivo del gradiente. Es que el gradiente en las primeras capas es el producto de miembros de todas las otras capas. Y cuando hay muchas capas, la situación se vuelve esencialmente inestable. Y la única forma en que todas las capas pueden aprender aproximadamente a la misma velocidad es elegir los miembros del trabajo que se equilibrarán entre sí. Y en ausencia de algún mecanismo o razón para tal equilibrio, es poco probable que esto suceda por casualidad.En resumen, el verdadero problema es que NS sufre el problema de un gradiente inestable. Y al final, si utilizamos técnicas de aprendizaje basadas en gradientes estándar, diferentes capas de la red aprenderán a velocidades terriblemente diferentes.

Ejercicio

• , |σ′(z)|<1/4. , , . ?

Hemos visto que el gradiente puede desaparecer o crecer explosivamente en las primeras capas de una red profunda. De hecho, cuando se usan neuronas sigmoides, el gradiente generalmente desaparecerá. Para entender por qué, considere nuevamente la expresión | wσ ′ (z) |. Para evitar el problema de gradiente que desaparece, necesitamos | wσ ′ (z) | ≥1. Puede decidir que esto es fácil de lograr con valores muy grandes de w. Sin embargo, en realidad no es tan simple. La razón es que el término σ ′ (z) también depende de w: σ ′ (z) = σ ′ (wa + b), donde a es la activación de entrada. Y si hacemos que w sea grande, debemos tratar de no hacer σ ′ (wa + b) pequeño en paralelo. Y esto resulta ser una limitación seria. La razón es que cuando hacemos w grande, hacemos wa + b muy grande. Si nos fijamos en la gráfica de σ ′, se puede ver que esto nos lleva a las "alas" de la función σ ′,donde toma valores muy pequeños. Y la única forma de evitar esto es mantener la activación entrante en un rango de valores bastante estrecho. A veces esto sucede por accidente. Pero más a menudo esto no sucede. Por lo tanto, en el caso general, tenemos el problema de un gradiente de fuga.

• |wσ′(wa+b)|. , |wσ′(wa+b)|≥1. , , |w|≥4.
• , |w|≥4, , |wσ′(wa+b)|≥1.
• , , ,

  $$

  $$\frac{2}{|w|} \ln\left( \frac{|w|(1+\sqrt{1-4/|w|})}{2}-1\right) \tag{123}$$
• , |w|≈6.9, ≈0,45. , , , .
• . x, w ₁ , b w ₂ . , , , w ₂ σ(w ₁ x+b)≈x for x∈[0,1]. , , ( ). : x=1/2+Δ, , w ₁ , w ₁ Δ .

Estudiamos redes de juguetes con solo una neurona en cada capa oculta. ¿Qué pasa con las redes profundas más complejas que tienen muchas neuronas en cada capa oculta?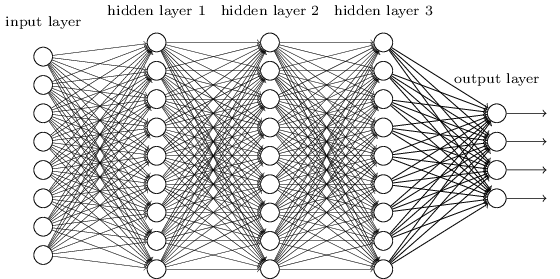



De hecho, sucede lo mismo en tales redes. Anteriormente en el capítulo sobre propagación hacia atrás, vimos que el gradiente en la capa #l de una red con capas L se especifica como:

$$

$$\delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}$$

Aquí Σ ′ (z ^l ) es la matriz diagonal, cuyos elementos son los valores de σ ′ (z) para las entradas ponderadas de la capa No. l. w ^l son matrices de peso para diferentes capas. Y ∇ _a C es el vector de derivadas parciales de C con respecto a las activaciones de salida.

Esta expresión es mucho más complicada que el caso con una neurona. Y, sin embargo, si miras detenidamente, su esencia será muy similar, con un montón de pares de la forma (w ^j ) ^T Σ ′ (z ^j ). Además, las matrices Σ ′ (z ^j ) en diagonal tienen valores pequeños, no más de 1/4. Si las matrices de peso w ^j no son demasiado grandes, cada término adicional (w ^j ) ^T Σ ′ (z ^l) tiende a disminuir el vector de gradiente, lo que conduce a un gradiente que desaparece. En el caso general, un mayor número de términos de multiplicación conduce a un gradiente inestable, como en nuestro ejemplo anterior. En la práctica, empíricamente en redes sigmoideas, los gradientes en las primeras capas desaparecen exponencialmente rápidamente. Como resultado, el aprendizaje en estas capas se ralentiza. Y la desaceleración no es un accidente o un inconveniente: es una consecuencia fundamental de nuestro enfoque de aprendizaje elegido.

Otros obstáculos para el aprendizaje profundo.

En este capítulo, me concentré en los gradientes que se desvanecen, y en general en el caso de los gradientes inestables, como un obstáculo para el aprendizaje profundo. De hecho, los gradientes inestables son solo un obstáculo para el desarrollo de la defensa civil, aunque importante y fundamental. Una parte importante de la investigación actual está tratando de comprender mejor los problemas que pueden surgir en la enseñanza de GO. No describiré en detalle todos estos trabajos, pero quiero mencionar brevemente un par de trabajos para darle una idea de algunas preguntas formuladas por la gente.

Como primer ejemplo en 2010Se encontró evidencia de que el uso de funciones de activación sigmoidea puede conducir a problemas con el aprendizaje de NS. En particular, se encontró evidencia de que el uso de un sigmoide conducirá al hecho de que las activaciones de la última capa oculta durante el entrenamiento estarán saturadas en la región 0, lo que ralentizará seriamente el entrenamiento. Se han propuesto varias funciones de activación alternativas que no sufren tanto por el problema de saturación (véase también otro documento de discusión ).

Como primer ejemplo, en 2013, se estudió el efecto de la inicialización aleatoria de los pesos y el gráfico de impulso en un descenso de gradiente estocástico basado en un impulso en el GO. En ambos casos, una buena elección influyó significativamente en la capacidad de entrenar STS.

Estos ejemplos sugieren que la pregunta "¿Por qué es tan difícil entrenar a STS?" muy complicado En este capítulo, nos centramos en las inestabilidades asociadas con el entrenamiento de gradiente de GNS. Los resultados de los dos párrafos anteriores indican que la elección de la función de activación, el método de inicialización de pesas e incluso los detalles de la implementación del entrenamiento basado en el descenso del gradiente también juegan un papel. Y, por supuesto, la elección de la arquitectura de red y otros hiperparámetros será importante. Por lo tanto, muchos factores pueden desempeñar un papel en la dificultad de aprender redes profundas, y la cuestión de comprender estos factores es el tema de una investigación en curso. Pero todo esto parece bastante sombrío e inspira pesimismo. Sin embargo, hay buenas noticias: en el próximo capítulo envolveremos todo a nuestro favor y desarrollaremos varios enfoques en GO,que en cierta medida podrá superar o sortear todos estos problemas.