
En 1985, el Instituto de Ingenieros Eléctricos y Electrónicos (
IEEE ) estableció el estándar
IEEE 754 , que es responsable de
los formatos de
coma flotante y aritmética, que será el modelo para todo el hardware y software durante los próximos 30 años.
Y aunque la mayoría de los programadores usan un punto flotante en cualquier momento indiscriminadamente, cuando necesitan realizar operaciones matemáticas con números reales, debido a ciertas restricciones en la representación de estos números, la velocidad y precisión de tales operaciones a menudo dejan mucho que desear.
Durante muchos años, el estándar fue duramente criticado por los científicos informáticos que estaban familiarizados con estos problemas, pero
John Gustafson se destacó entre ellos y realizó una cruzada para reemplazar el punto flotante con algo más adecuado. En este caso, posit o
unum se considera una opción más adecuada: la tercera opción es el resultado de su estudio de "números universales". Él dice que los números positivos resolverán la mayoría de los problemas principales del estándar IEEE 754, brindarán un mejor rendimiento y precisión, y usarán menos bits. Lo que es aún mejor, afirma que el nuevo formato puede reemplazar los números de punto flotante estándar "sobre la marcha", sin tener que cambiar el código fuente de las aplicaciones.
Nos reunimos con Gustafson en la conferencia ISC19. Y para los especialistas en supercomputadoras ubicados allí, una de las principales ventajas del formato positivo es que puede lograr una mayor precisión y rango dinámico utilizando menos bits que números de IEEE 754. Y no solo un poco menos. Gustafson dijo que el positivo de 32 bits reemplaza el flotante de 64 bits en casi todos los casos, lo que podría tener serias consecuencias para la informática científica. Si reduce a la mitad el número de bits, no solo puede reducir el caché, la memoria y el almacenamiento de estos números, sino que también puede reducir seriamente el ancho del canal requerido para transferirlos al procesador y viceversa. Esta es la razón principal por la cual la aritmética basada en posit, en su opinión, dará una velocidad de cálculo de doble a cuádruple en comparación con los números de coma flotante IEEE.
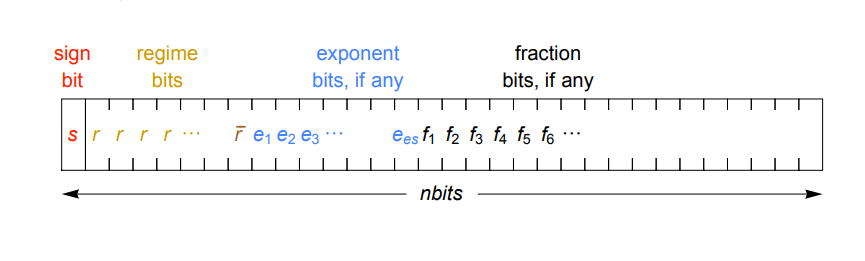
La aceleración se puede lograr a través de una representación compacta de números reales. En lugar del exponente y la parte fraccionaria de un tamaño fijo utilizado en el estándar IEEE, posit codifica el exponente con un número variable de bits (una combinación de bits de modo y bits de exponente), de modo que en la mayoría de los casos se requieren menos. Como resultado, quedan más bits en la parte fraccionaria, lo que proporciona una mayor precisión. Vale la pena usar un exponente dinámico debido a su precisión cónica. Esto significa que los valores con un exponente pequeño, que se usan con mayor frecuencia, pueden tener mayor precisión, y los números muy grandes y muy pequeños que se usan con menos frecuencia tendrán menos precisión.
El trabajo de Gustafson en 2017 que describe el formato positivo ofrece una descripción detallada de cómo funciona.
Otra ventaja importante del formato es que, a diferencia de los números de coma flotante ordinarios, posit da los mismos resultados bit a bit en cualquier sistema, lo que a menudo no se puede garantizar con el formato de IEEE (aquí incluso los mismos cálculos en el mismo sistema pueden dar diferentes resultados). Además, el nuevo formato se ocupa de los errores de redondeo, desbordamiento y desaparición de dígitos significativos, números desnormalizados y muchos valores del tipo no un número (NaN). Además, posit evita rarezas como los valores 0 y -0 que no coinciden. En cambio, el formato utiliza un complemento binario para el carácter, como enteros, lo que significa que la comparación bit a bit funcionará correctamente.
Algo llamado quire está asociado con los números positivos, un mecanismo de acumulación que permite a los programadores realizar álgebra lineal reproducible, un proceso que no está disponible para los números IEEE regulares. Admite la operación generalizada de multiplicación-suma combinada y otras operaciones combinadas que le permiten calcular productos escalares o sumas sin errores de redondeo o desbordamientos. Las pruebas iniciadas en la Universidad de California en Berkeley demostraron que las operaciones de quire son de 3 a 6 veces más rápidas que la ejecución secuencial. Gustafson dice que permiten que los números positivos "peleen fuera de su categoría de peso".
Aunque este formato de número solo existe desde hace un par de años, la comunidad de informática de alto rendimiento (HPC) ya tiene interés en explorar sus aplicaciones. Por el momento, todo el trabajo sigue siendo experimental y se basa en la velocidad esperada del futuro hardware o en el uso de herramientas que emulan la aritmética positiva en los procesadores convencionales. Mientras que en producción no hay chips que implementen posit a nivel de hardware.
Una de las aplicaciones potenciales del formato es el radio interferómetro de
matriz de kilómetros cuadrados (SKA) en construcción, cuando lo diseñan
consideran los números positivos como una forma de reducir radicalmente el ancho del canal y la carga computacional para procesar datos provenientes del radiotelescopio. Es necesario que las supercomputadoras que lo atienden consuman no más de 10 MW, y una de las formas más prometedoras para lograr esto, según los diseñadores, es usar un formato positivo más denso para reducir a la mitad el ancho estimado del canal de memoria (200 PB / s), el canal de transmisión datos (10 TB / s) y conexión de red (1 TB / s). El poder de cómputo también debería aumentar.
Otra aplicación es para usar en predicciones meteorológicas y predicciones climáticas. El equipo británico
demostró que los números positivos de 16 bits están claramente por delante de los números estándar de coma flotante de 16 bits y que "tienen un gran potencial para su uso en modelos más complejos". La emulación positiva de 16 bits en este modelo funcionó tan bien como los números de coma flotante de 64 bits.
El Laboratorio Nacional de Livermore
evalúa los formatos de números positivos y otros, explorando formas de reducir la cantidad de datos que se moverán en los supercomputadores exaflops del futuro. En algunos casos, también obtuvieron mejores resultados. Por ejemplo, los números positivos lograron una precisión superior en cálculos físicos como la hidrodinámica de choque y, en general, superaron a los números de coma flotante en varias dimensiones.

Quizás posit tendrá el mayor potencial en el aprendizaje automático, donde los números de 16 bits se pueden usar para el aprendizaje, y los números de 8 bits se pueden usar para la verificación. Gustafson dijo que los números de coma flotante de 32 bits son excesivos para el entrenamiento, y en algunos casos ni siquiera muestran resultados tan buenos como el positivo de 16 bits, explicando que el estándar IEEE 754 "no estaba destinado para usarse con IA" .
No es sorprendente que la comunidad de IA les haya prestado atención. Facebook Jeff Johnson ha desarrollado una plataforma experimental con FGPA usando posit, que muestra una mejor eficiencia energética en comparación con float16 y bfloat16 de IEEE para tareas de aprendizaje automático. Planean explorar el uso de hardware quire de 16 bits para la capacitación y compararlos con formatos competitivos.
Vale la pena señalar que Facebook está
trabajando con Intel en el procesador Nervana Neural Network (NNP), lo que debería acelerar algunas de las tareas relacionadas con la inteligencia artificial del gigante social. No se descarta la opción de usar el formato positivo, aunque es más probable que Intel deje su formato FlexPoint original para Nervana. En cualquier caso, vale la pena seguir este punto.
Gustafson conoce al menos un chip AI en el que intentan usar números positivos en el diseño, aunque no tiene derecho a divulgar el nombre de la empresa. La compañía francesa Kalray, que trabaja con la Iniciativa Europea de Procesadores (EPI), también ha mostrado interés en apoyar posit en su acelerador de matriz de procesador paralelo masivo (MPPA) de próxima generación, por lo que esta tecnología puede ir a
los supercomputadores exaflops europeos .
Para Gustafson, todo esto, por supuesto, inspira, y él cree que este tercer intento de avanzar en sus números universales puede tener éxito. A diferencia de las versiones uno y dos, posit es fácil de implementar en hardware. Y dada la feroz competencia en el campo de la IA, quizás deberíamos esperar el éxito comercial del nuevo formato. Entre otras plataformas en las que posit puede esperar un futuro brillante están el procesamiento de señal digital, GPU (para gráficos y otras computadoras), dispositivos para Internet de las cosas, computación de borde. Y, por supuesto, HPC.
Si la tecnología se distribuye comercialmente, es poco probable que Gustafson pueda capitalizar su éxito. Su proyecto, como se indica en el estándar de 10 páginas, está completamente abierto y está disponible para su uso por cualquier empresa que desee desarrollar el software y el hardware adecuados. Lo que probablemente explica la atención a la tecnología de compañías como IBM, Google, Intel, Micron, Rex Computing, Qualcomm, Fujitsu, Huawei y muchas otras.
Sin embargo, reemplazar el IEEE 754 con algo más adecuado es un gran proyecto, incluso para una persona con un currículum tan impresionante como el de Gustafson. Incluso antes de trabajar en ClearSpeed, Intel y AMD, estudió formas de mejorar los cálculos científicos en procesadores modernos. "He estado tratando de resolver este problema durante los últimos 30 años", dijo.