
Una de las tareas más importantes en el aprendizaje automático es la detección de objetos. Recientemente, se han publicado una serie de algoritmos de aprendizaje automático basados en Deep Learning para la detección de objetos. Estos algoritmos ocupan un lugar central en las aplicaciones prácticas de visión por computadora, en particular, los autos de conducción autónoma actualmente muy populares. Pero todos estos métodos son métodos de enseñanza con un maestro, es decir. necesitan un gran conjunto de datos (gran conjunto de datos). Naturalmente, existe el deseo de tener un modelo capaz de aprender de datos "en bruto" (no asignados). Traté de analizar los métodos existentes y también indicar posibles formas de su desarrollo. Le pregunto a todos los que desean misericordia bajo Kat, será interesante.
Estado actual de la pregunta.
Naturalmente, la formulación de este problema ha existido durante mucho tiempo (casi desde los primeros días de la existencia del aprendizaje automático) y hay un número suficiente de trabajos sobre este tema. Por ejemplo, uno de mis
detectores de objetos no supervisados espacialmente invariables favoritos
con redes neuronales convolucionales . En resumen, los autores están entrenando el Codificador automático variable (VAE), pero este enfoque plantea una serie de preguntas para mí.
Un poco de filosofia
Entonces, ¿qué es un objeto en una imagen? Para responder a esta pregunta, debemos responder la pregunta: ¿por qué incluso dividimos el mundo en objetos? Después de reflexionar un poco sobre esta pregunta, solo tenía una respuesta a esta pregunta (no digo que no haya otras, simplemente no las encontré): estamos tratando de encontrar una representación del mundo que nos sea fácil de entender y controlar la cantidad de información necesaria para describir el mundo. en el contexto de la tarea actual. Por ejemplo, para la tarea de clasificar imágenes (que generalmente está formulada incorrectamente, rara vez hay imágenes con un objeto. Es decir, resolvemos el problema, no lo que se muestra en la imagen, sino qué objeto es "principal"), solo tenemos que decir que la imagen es "automóvil" , a su vez, para la tarea de detectar objetos, queremos saber qué objetos "interesantes" (no nos interesan todas las hojas de los árboles en la imagen) y dónde están, para la tarea de describir la escena, queremos obtener el nombre del proceso "interesante" sucede allí, por ejemplo, "puesta de sol", etc.
Resulta que los objetos son una representación conveniente de los datos. ¿Qué propiedades debe tener esta representación? La vista debe contener la mayor cantidad posible de información completa sobre la imagen. Es decir teniendo una descripción del objeto, queremos poder restaurar la imagen original con el grado de precisión necesario.
¿Cómo se puede expresar esto matemáticamente? Imagine que la imagen es una realización de una variable aleatoria X, y la representación será una realización de una variable aleatoria Y. En vista de lo anterior, queremos que Y contenga tanta información como sea posible sobre X. Naturalmente, para hacer esto, use el concepto de información mutua.
Modelos de aprendizaje automático para obtener la máxima información.
La detección de objetos puede considerarse como un modelo generativo, que recibe una imagen en la entrada
x , y la salida es una representación de objeto de la imagen
y .

Recordemos ahora la fórmula para calcular la información mutua:
I(x,y)= intp(x,y)log fracp(x,y)p(x)p(y)dxdy
donde
p(x,y) distribución de densidad conjunta también
p(x),p(y) marginados
Aquí no profundizaré por qué esta fórmula se ve así, pero creeremos que internamente es muy lógico. Por cierto, según las consideraciones descritas, no es necesario elegir exactamente información mutua, puede ser cualquier otra "información", pero volveremos a esto más cerca del final.
Particularmente atento (o aquellos que leen libros sobre la teoría de la información) ya han notado que la información mutua no es más que la divergencia Kullback-Lebler entre la distribución conjunta y el trabajo de los marginales. Aquí surge una pequeña complicación: cualquiera que haya leído al menos un par de libros sobre aprendizaje automático sabe que si solo tenemos muestras de dos distribuciones (es decir, no conocemos las funciones de distribución), entonces ni siquiera está optimizando, sino incluso evaluando la divergencia de Kullback, La tarea de Leibler es muy no trivial. Además, nuestras queridas GAN nacieron precisamente por esta razón.
Afortunadamente, la maravillosa idea de utilizar el límite de variación inferior descrito en
On Variational Bounds of Mutual Information nos ayuda. La información mutua se puede representar como:
I(x,y)= intp(x)dx intp(y|x)log[q(x|y)]dxdy+ intp(y)dy intp(x|y)log( fracp(x|y)q(x|y)dxdy
O
I(x,y)= intp(x)dx intp(y|x)log[q(x|y)]dxdy+KL[p(x|y)||q(x|y)]
donde
p(y|x) - la distribución de la representación para una imagen dada, parametrizada por nuestra red neuronal y de esta distribución podemos muestrear, pero no necesitamos poder estimar la densidad o probabilidad de una muestra en particular (que generalmente es típica de muchos modelos generativos).
q(x|y) Es una determinada función de densidad parametrizada por la segunda red neuronal (en el caso más general, necesitamos 2 redes neuronales, aunque en algunos casos pueden ser representadas por la primera), aquí debemos poder calcular las probabilidades de las muestras resultantes.
Valor
LVB(x,y)= intp(x)dx intp(y|x)log[q(x|y)]dxdy llamado el límite variacional inferior.
Ahora podemos resolver el enfoque de nuestro problema, es decir, aumentar no la información mutua en sí, sino su límite de variación más bajo. Si la distribución
q(x|y) elegido correctamente, entonces en el punto máximo del límite de variación y la información mutua coincidirán, pero en el caso práctico (cuando la distribución
q(x|y) no puedo imaginar exactamente
p(x|y) , pero consiste en una familia bastante grande de funciones) estará muy cerca, lo que también nos conviene.
Si alguien no sabe cómo funciona esto, le aconsejo que considere cuidadosamente el algoritmo EM. Aquí hay un caso completamente similar.
¿Qué está pasando aquí? De hecho, tenemos la funcionalidad para entrenar codificador automático. Si Y es el resultado a la salida de una red neuronal con alguna imagen en la entrada, entonces esto significa que
p(y|x)= delta(enc(x)) donde
enc(x) función de transformación de la red neuronal. Y aproximar la distribución inversa por gaussiano, es decir
log[q(x|y)]=(x−dec(y))2−2∗log(sigma) obtenemos:
LVB(x,y)= intp(x)(x−dec(enc(x)))2dx+C
Y esta es una característica clásica para el codificador automático.
El codificador automático no es suficiente
Creo que muchos ya quieren entrenar el codificador automático y esperan que en su capa oculta haya neuronas que respondan a objetos específicos. En general, hay una confirmación de algo similar y resulta la
creación de características de alto nivel mediante el aprendizaje no supervisado a gran escala . Pero aún así esto es completamente poco práctico. Y las personas más atentas ya se han dado cuenta de que los autores de este artículo utilizaron la regularización: agregaron un término que proporciona escasez en la capa oculta y escribieron en blanco y negro que nada de eso ocurre sin este término.
¿El principio de maximizar la información mutua es suficiente para aprender una idea "conveniente"? Obviamente no, porque podemos elegir Y igual a X (es decir, usar la imagen como su representación) o cualquier transformación biyectiva, la información mutua llega al infinito en este caso. No puede haber más de este valor, pero como sabemos, esta es una idea muy pobre.
Necesitamos un criterio adicional para la "conveniencia" de la presentación. Los autores del artículo anterior consideraron la escasez como "conveniencia". Este es un tipo de realización de la hipótesis de que debería haber algunos "objetos importantes" en la imagen. Pero iremos más allá: queremos no solo aprender el hecho de que dicho objeto está en la imagen, sino también saber dónde está, cuánto se superpone, etc. Surge la pregunta, ¿cómo hacer que la red neuronal interprete la salida de una neurona como, por ejemplo, la coordenada de un objeto? La respuesta es obvia: el resultado de esta neurona debe usarse precisamente para esto. Es decir, conociendo la idea, debemos ser capaces de generar imágenes "similares" a la original.
La idea general fue tomada de los chicos de Facebook.
El codificador se verá así:

donde
A - algún vector que describe el objeto,
x,y - coordenadas del objeto,
sx,sy - la escala del objeto,
z - la posición del objeto en profundidad,
p - la probabilidad de que el objeto esté presente.
Es decir, la red neuronal de entrada recibe una imagen de un tamaño predeterminado en el que queremos encontrar objetos y emite una serie de descripciones. Si queremos una red de un solo paso, desafortunadamente esta matriz tendrá que tener un tamaño fijo. Si queremos encontrar todos los objetos, tendremos que usar redes de reclutamiento.
El decodificador será así:
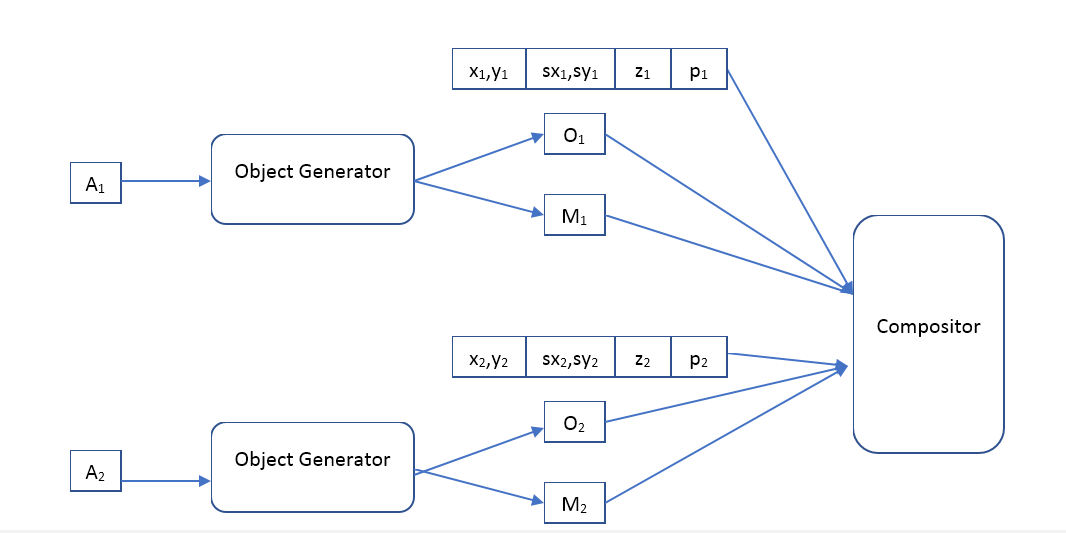
Donde Object Generator es una red que recibe un vector de descripción de objeto en la entrada y proporciona
O - la imagen (de cierto tamaño estándar) del objeto y la máscara de píxeles opacos (máscara de opacidad).
Compositor: recibe la imagen de entrada de todos los objetos, máscara, posición, escala, profundidad y forma la imagen de salida, que debería ser similar a la original.
¿Cuál es la diferencia entre nuestro enfoque y VAE?
Parece que queremos usar un codificador automático con la misma arquitectura que los autores del artículo
Detección de objetos no supervisados espacialmente invariables con redes neuronales convolucionales , por lo que la pregunta es cuál es la diferencia. Tanto allí como allí autoencoder, solo en la segunda versión es variacional.
Desde un punto de vista teórico, la diferencia es muy grande. VAE es un modelo generativo y su tarea es hacer 2 distribuciones (imágenes iniciales y generadas) lo más similar posible. En términos generales, VAE no garantiza que la imagen generada a partir de la "descripción" de un objeto generado a partir de la imagen original sea al menos ligeramente similar al original. Por cierto, los autores de VAE
Auto-Encoding Variational Bayes hablan sobre esto. Entonces, ¿por qué sigue funcionando? Creo que la arquitectura seleccionada de las redes neuronales y la "descripción" ayudan a aumentar la información mutua de la imagen y la "descripción", pero no pude encontrar ninguna evidencia matemática para esta hipótesis. Una pregunta para los lectores: ¿alguien puede explicar los resultados de los autores? Su imagen restaurada es muy similar a la original, ¿por qué?
Además, el uso de VAE obliga a los autores a especificar la distribución de "descripciones", y el método para maximizar la información mutua no hace suposiciones al respecto. Lo que nos da libertad adicional, por ejemplo, podemos intentar agrupar vectores en un modelo ya entrenado
A descripciones, y mira, ¿tal vez tal sistema aprenderá las clases de objetos? Cabe señalar que tal agrupación usando VAE no tiene ningún sentido, por ejemplo, los autores del artículo usan una distribución gaussiana para estos vectores.
Los experimentos
Desafortunadamente, ahora el trabajo lleva una gran cantidad de tiempo y no es posible completarlo en un tiempo aceptable. Si alguien quiere escribir varios miles de líneas de código, capacitar a cientos de modelos de aprendizaje automático y realizar muchos experimentos interesantes, simplemente porque le da placer (a ella), estaré encantado de unir fuerzas. Escribe en un personal.
El campo para los experimentos aquí es muy amplio. Tengo planes de comenzar entrenando el auto codificador clásico (mapeo determinista de imágenes a descripciones y una distribución inversa gaussiana) y ver qué aprende. En los primeros experimentos, será suficiente usar el compositor descrito por los chicos de Facebook, pero en el futuro creo que será muy interesante tocar con varios compositores, y es posible hacerlos también aprendebles. Compare diferentes regularizadores: sin él, disperso, etc. Compare el uso de modelos feedforward y recursivos. Luego, use modelos de distribución más avanzados para la distribución inversa, por ejemplo, una
estimación de densidad como Real NVP . Vea cómo mejora o empeora con los modelos más flexibles. Vea lo que sucederá si la visualización de imágenes en las descripciones se hace no determinista (generada a partir de alguna distribución condicional). Y finalmente, intente aplicar varios métodos de agrupamiento a los vectores de descripción
A y entender si dicho sistema puede aprender clases de objetos.
Pero lo más importante, realmente quiero comparar la calidad del modelo basado en maximizar la información mutua y el modelo con VAE.