Hilbert, Lebesgue ... y el vacío

Bajo el corte, se investiga la cuestión de cómo se debe organizar un buen algoritmo de indexación multidimensional. Sorprendentemente, no hay tantas opciones.

Índices unidimensionales, árboles B

La medida del éxito del algoritmo de búsqueda se considerará 2 hechos:

1. el establecimiento del hecho de su presencia o ausencia de un resultado ocurre para el número logarítmico (con respecto al tamaño del índice) de lecturas de páginas de disco
2. el costo de emitir un resultado es proporcional a su volumen

En este sentido, los árboles B tienen bastante éxito y la razón de esto puede considerarse el uso de un árbol equilibrado. La simplicidad del algoritmo se debe a la unidimensionalidad del espacio clave: si es necesario, divida la página, es suficiente dividir por la mitad el conjunto ordenado de elementos de esta página. Generalmente dividido por el número de elementos, aunque esto no es necesario.

Porque las páginas del árbol se almacenan en el disco, se puede decir que el árbol B tiene la capacidad de convertir de manera muy eficiente el espacio clave unidimensional en espacio unidimensional.

Al llenar un árbol con más o menos "inserción correcta", y este es un caso bastante común, las páginas se generan en el orden de crecimiento de la clave, alternando de vez en cuando con páginas más altas. Hay buenas posibilidades de que también estén en el disco. Por lo tanto, sin ningún esfuerzo, se logra una alta localidad de datos: los datos que tienen un valor cercano estarán en algún lugar cercano y en el disco.

Por supuesto, al insertar valores en orden aleatorio, las claves y las páginas se generan aleatoriamente, como resultado de lo cual fragmentación del índice. También hay herramientas antifragmentación que restauran la localidad de datos.

Parece que en nuestra era de discos RAID y SSD, el orden de lectura del disco no importa. Pero, más bien, no tiene el mismo significado que antes. No hay reenvío físico de los cabezales en el SSD, por lo que su velocidad de lectura aleatoria no disminuye cientos de veces en comparación con la lectura sólida, como un HDD. Y solo una vez cada 10 o más .

Recordemos que los árboles B aparecieron en 1970 en la era de las cintas y tambores magnéticos. Cuando la diferencia en la velocidad de acceso aleatorio para la cinta y el tambor mencionados fue mucho más dramática que en comparación con HDD y SSD.

Además, 10 veces también importan. Y estas 10 veces incluyen no solo las características físicas del SSD, sino también el punto fundamental: la previsibilidad del comportamiento del lector. Si es muy probable que el lector solicite el siguiente bloque para este bloque, tiene sentido descargarlo de manera proactiva, por supuesto. Y si el comportamiento es caótico, todos los intentos de predicción no tienen sentido e incluso son dañinos.

Indexación multidimensional

Además, trataremos el índice de puntos bidimensionales (X, Y), simplemente porque es conveniente e intuitivo trabajar con ellos. Pero los problemas son básicamente los mismos.

Una opción simple, "poco sofisticada" con índices separados para X e Y no pasa de acuerdo con nuestro criterio de éxito. No da el costo logarítmico de obtener el primer punto. De hecho, para responder la pregunta, ¿hay algo en absoluto en la medida deseada, debemos

• haga una búsqueda en el índice X y obtenga todos los identificadores de la extensión del intervalo X
• similar para Y
• intersecar estos dos conjuntos de identificadores

El primer elemento ya depende del tamaño de la extensión y no garantiza el logaritmo.

Para ser "exitoso", un índice multidimensional debe organizarse como un árbol más o menos equilibrado. Esta declaración puede parecer controvertida. Pero el requisito de una búsqueda logarítmica nos dicta tal dispositivo. ¿Por qué no dos árboles o más? Ya considerada la opción "poco sofisticada" e inadecuada con dos árboles. Quizás hay los adecuados. Pero dos árboles: esto es el doble de cerraduras (incluidas las simultáneas), el doble de costo, posibilidades significativamente mayores de atrapar un punto muerto. Si puedes sobrevivir con un árbol, definitivamente deberías usarlo.

Dado todo esto, el deseo de tomar como base la exitosa experiencia del árbol B y "generalizarla" para que funcione con datos bidimensionales es bastante natural.

Entonces apareció el árbol R.

Árbol R

El árbol R está organizado de la siguiente manera:
Inicialmente, tenemos una página en blanco, solo agregue datos (puntos).
Pero aquí la página está llena y debe dividirse.
En el árbol B, los elementos de la página están ordenados de forma natural, por lo que la pregunta es cuánto cortar. No hay un orden natural en el árbol R. Hay dos opciones:

• Traer orden, es decir introduce una función que, basada en X&Y, dará un valor de acuerdo con los elementos de la página que se ordenarán y dividirán de acuerdo con ellos. En este caso, todo el índice degenera en un árbol B regular construido a partir de los valores de la función especificada. Además de las ventajas obvias, hay una gran pregunta: bueno, bueno, indexamos, pero ¿cómo mirar? Más sobre eso más adelante, primero considere la segunda opción.
• Divide la página por criterios espaciales. Para hacer esto, a cada página se le debe asignar la extensión de los elementos ubicados en / debajo de ella. Es decir la página raíz tiene la extensión de toda la capa. Al dividir, se generan dos (o más) páginas cuyas extensiones se incluyen en la extensión de la página principal (para búsqueda).

Hay pura incertidumbre. ¿Cómo exactamente dividir la página? Horizontal o vertical? ¿Procede de la mitad del área o la mitad de los elementos? Pero, ¿qué pasa si los puntos formaron dos grupos, pero solo puede separarlos con una línea diagonal? ¿Y si hay tres grupos?

---

La mera presencia de tales preguntas indica que el árbol R no es un algoritmo. Este es un conjunto de heurísticas, al menos para dividir una página durante la inserción, para fusionar páginas durante la eliminación / modificación, para el preprocesamiento para la inserción masiva.

La heurística implica la especialización de un árbol particular en un tipo de datos particular. Es decir en conjuntos de datos de cierto tipo, ella comete errores con menos frecuencia. "La heurística no puede estar completamente equivocada, porque en este caso, sería un algoritmo ”©.

¿Qué significa el error heurístico en este contexto? Por ejemplo, que la página se dividirá / fusionará sin éxito y las páginas comenzarán a superponerse parcialmente entre sí. Si de repente la extensión de la búsqueda cae en el área de superposición de las páginas, el costo de la búsqueda ya no será del todo logarítmico. Con el tiempo, a medida que inserta / elimina, la cantidad de errores se acumula y el rendimiento del árbol comienza a degradarse.


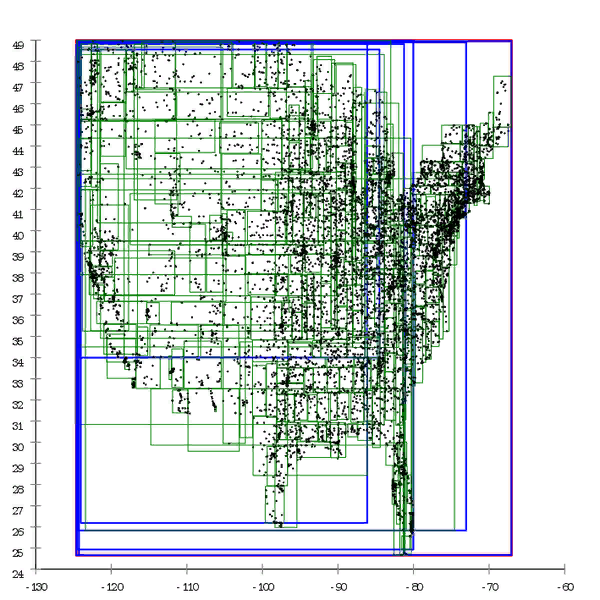Figura 1 Aquí hay un ejemplo de un árbol R *, que se construye de forma natural.


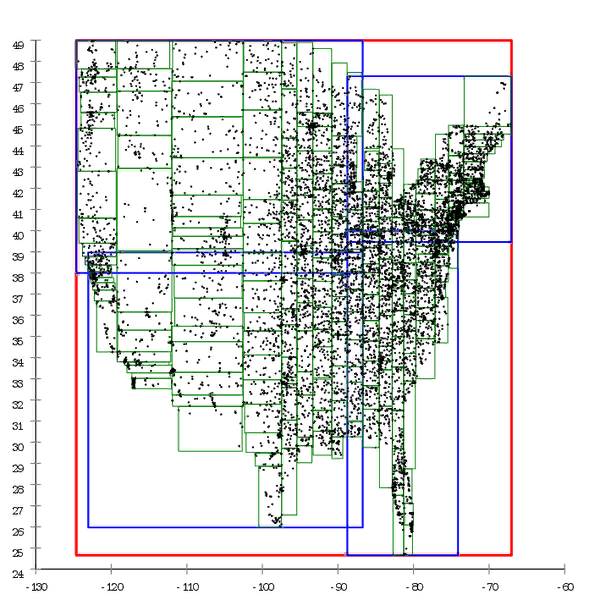Figura 2 Y aquí el mismo conjunto de datos se procesa previamente y el árbol se construye mediante inserción masiva

Podemos decir que el árbol B también se degrada con el tiempo, pero esta es una degradación ligeramente diferente. El rendimiento del árbol B disminuye debido al hecho de que sus páginas no están en una fila. Esto se trata fácilmente al "enderezar" el árbol: la desfragmentación. En el caso de un árbol R, no es tan fácil deshacerse de él; la estructura del árbol en sí es "curva" para corregir la situación; necesita ser completamente reconstruido.

Las generalizaciones del árbol R a espacios multidimensionales no son obvias. Por ejemplo, al dividir páginas, minimizamos el perímetro de las páginas secundarias. ¿Qué minimizar en el caso tridimensional? Volumen o área de superficie? ¿Y en el caso de ocho dimensiones? El sentido común ya no es un asesor.

El espacio indexado puede ser no isotrópico. ¿Por qué no indexar no solo los puntos, sino también sus posiciones en el tiempo, es decir? (X, Y, t). En este caso, por ejemplo, las heurísticas basadas en el perímetro no tienen sentido ya que apila la longitud a intervalos de tiempo.

La impresión general del árbol R es algo así como crustáceos con patas branquiales . Esos tienen su propio nicho ecológico en el que es difícil competir con ellos. Pero en el caso general, no tienen posibilidades de competir con animales más desarrollados.

Árbol cuádruple

En un árbol cuádruple, cada página que no es hoja tiene exactamente cuatro descendientes, que dividen igualmente su espacio en cuadrantes.


Figura 3 Ejemplo de un árbol cuádruple construido

Este no es un buen diseño de base de datos.

• Cada página reduce el espacio de búsqueda para cada coordenada solo dos veces. Sí, esto proporciona la complejidad logarítmica de la búsqueda, pero este es el logaritmo de base 2, no el número de elementos en la página, (incluso 100) como en un árbol B.
• Cada página es pequeña, pero detrás de ella todavía tienes que ir al disco.
• La profundidad del árbol cuádruple debe ser limitada, de lo contrario, su desequilibrio afecta el rendimiento. Como resultado, en datos altamente agrupados (por ejemplo, casas en un mapa, hay muchas ciudades en ciudades, pocas en campos), se puede acumular una gran cantidad de datos en las páginas de hoja. Un índice de uno exacto se vuelve bloqueado y requiere procesamiento posterior.
  
  Un tamaño de red mal seleccionado (profundidad del árbol) puede matar el rendimiento. Sin embargo, me gustaría que el rendimiento del algoritmo no dependa críticamente del factor humano.
  
• El costo del espacio para almacenar un punto es bastante grande.

Numeración espacial

Queda por considerar la versión previamente diferida con una función que, sobre la base de una clave multidimensional, calcula el valor para escribir en un árbol B normal.

La construcción de dicho índice es obvia, y el índice en sí tiene todas las ventajas del árbol B. La única pregunta es si este índice puede usarse para una búsqueda efectiva.

Hay una gran cantidad de tales funciones, se puede suponer que entre ellas hay una pequeña cantidad de "buenas", una gran cantidad de "malas" y una gran cantidad de "simplemente horribles".

Encontrar una función terrible no es difícil: serializamos la clave en una cadena, consideramos MD5 y obtenemos un valor que es completamente inútil para nuestros propósitos.

¿Y cómo acercarse a lo bueno? Ya se ha dicho que un índice útil proporciona "localidad" de datos, puntos que están cerca del espacio y que a menudo están cerca uno del otro cuando se guardan en el disco. Aplicado a la función deseada, esto significa que para puntos espacialmente cercanos da valores cercanos.

Una vez en el índice, los valores calculados aparecerán en las páginas "físicas" en el orden de sus valores. Desde el punto de vista del "sentido físico", la extensión de la búsqueda debería afectar la menor cantidad posible de páginas de índice físico. Lo que generalmente es obvio. Desde este punto de vista, las curvas de numeración que "extraen" los datos son "malas". Y aquellos que "confunden en una pelota" - más cerca de lo "bueno".

Numeración ingenua

Un intento de exprimir un segmento en un cuadrado (hipercubo) mientras permanece en la lógica del espacio unidimensional, es decir cortar en pedazos y llenar el cuadrado con estos pedazos. Podría ser


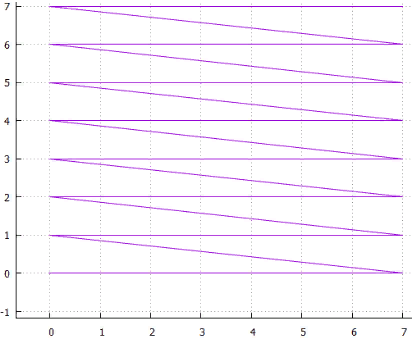Exploración de 4 líneas


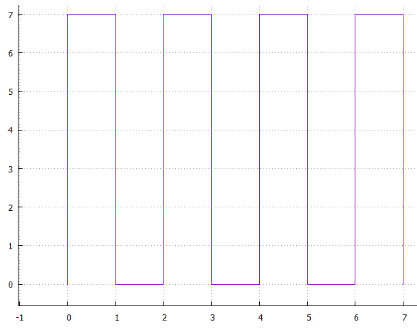5 entrelazados


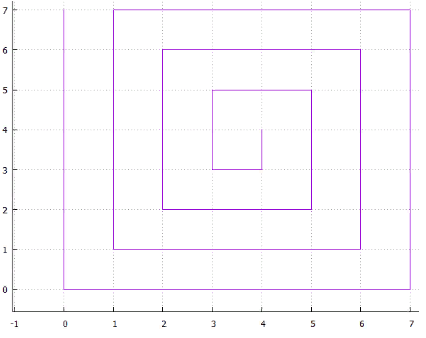Fig.6 espiral

o ... puedes encontrar muchas opciones, todas tienen dos inconvenientes

1. ambigüedad, por ejemplo: por qué la espiral está curvada en el sentido de las agujas del reloj y no contra ella, o por qué la exploración horizontal es primero a lo largo de X y luego a lo largo de Y
   
2. la presencia de piezas rectas largas que hacen que el uso de dicho método sea ineficaz para la indexación multidimensional (perímetro de página grande)

Funciones de acceso directo.

Si la afirmación principal de los métodos "ingenuos" es que generan páginas muy alargadas, generemos las páginas "correctas" por nuestra cuenta.

La idea es simple: permita que haya una división externa del espacio en bloques, asigne un identificador a cada bloque y esta será la clave del índice espacial.

• deje que las coordenadas X e Y sean de 16 bits (para mayor claridad)
• vamos a cubrir el espacio con bloques cuadrados de tamaño 1024X1024
• engrosar las coordenadas, cambiar 10 bits a la derecha
• y obtener la identificación de la página, pegue los bits de X&Y. Ahora en el identificador, los 6 dígitos inferiores son los más antiguos de X, los siguientes 6 dígitos son los más antiguos de Y
  

Es fácil ver que los bloques forman un escaneo de línea, por lo tanto, para encontrar datos para la extensión de búsqueda, tendrá que hacer una búsqueda / lectura en el índice para cada fila de bloques en la que se coloca esta extensión. En general, este método funciona muy bien, aunque tiene varias desventajas.

• Al crear un índice, debe elegir el tamaño de bloque óptimo, que es completamente obvio
• Si el bloque es significativamente mayor que una consulta típica, la búsqueda será ineficaz ya que tener que leer y filtrar (postprocesamiento) demasiado
  
• Si el bloque es significativamente más pequeño que una consulta típica, la búsqueda será ineficaz ya que tendrá que hacer muchas consultas fila por fila
  
• Si el bloque tiene demasiados o muy pocos datos en promedio, la búsqueda será ineficaz
  
• Si los datos están agrupados (por ejemplo, en casa en el mapa), la búsqueda no será efectiva en todas partes
• Si el conjunto de datos ha crecido, puede resultar que el tamaño del bloque haya dejado de ser óptimo.
  

Parcialmente, estos problemas se resuelven construyendo bloques de varios niveles. Por el mismo ejemplo:

• Todavía quiero bloques 1024X1024
• pero ahora todavía tendremos bloques de nivel superior de tamaño 8X8 bloques inferiores
• La clave está organizada de la siguiente manera (de menor a mayor):
  3 dígitos - dígitos 10 ... 12 coordenadas X
  3 dígitos - dígitos 10 ... 12 coordenadas Y
  3 dígitos - dígitos 13 ... 15 coordenadas X
  3 dígitos - dígitos 13 ... 15 coordenadas Y

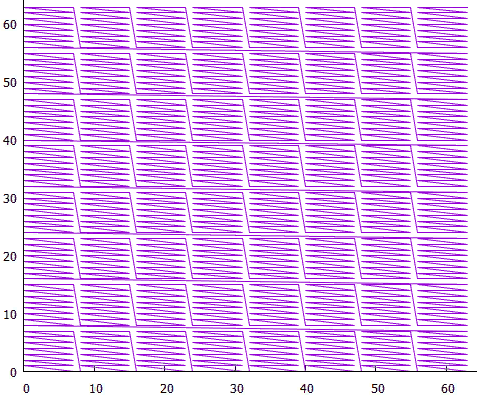7 bloques de bajo nivel forman bloques de alto nivel

Ahora, para grandes extensiones, no necesita leer una gran cantidad de bloques pequeños, esto se hace a expensas de los bloques de alto nivel.

Curiosamente, era posible no endurecer las coordenadas, sino de la misma manera presionarlas en la tecla. En este caso, el filtrado posterior sería más barato porque ocurriría al leer el índice.

Los índices de GRID espacial se organizan en MS SQL de manera similar; se permiten hasta 4 niveles de bloque en ellos.


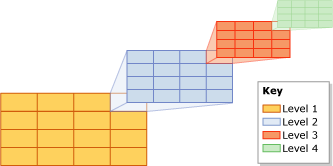Fig.8 índice GRID

Otra forma interesante de indexación directa es usar un árbol cuádruple para la partición externa del espacio.

El árbol cuádruple es útil porque puede adaptarse a la densidad de los objetos ya que cuando el nodo se desborda, se divide. Como resultado, donde la densidad de los objetos es alta, los bloques resultarán pequeños y viceversa. Esto reduce el número de llamadas de índice vacías.

Es cierto que el árbol cuádruple es una construcción inconveniente para la reconstrucción sobre la marcha, es ventajoso hacer esto de vez en cuando.

De lo agradable, al reconstruir un árbol cuádruple, no hay necesidad de reconstruir el índice si los bloques se identifican con el código de Morton y los objetos se codifican con él. Aquí está el truco: si las coordenadas del punto están codificadas con un código Morton, el identificador de página es un prefijo en ese código. Al buscar datos de página, se seleccionan todas las teclas que están en el rango de [prefijo] 00 ... 00B a [prefijo] 11 ... 11B, si la página se divide, significa que solo se ha alargado el prefijo de sus descendientes.

Características auto-similares

Lo primero que viene a la mente al mencionar funciones auto-similares es "curvas de barrido". "Una curva notable es un mapeo continuo, cuyo dominio es el segmento unitario [0, 1], y el dominio es el espacio euclidiano (más estrictamente, topológico)". Un ejemplo es la curva de Peano.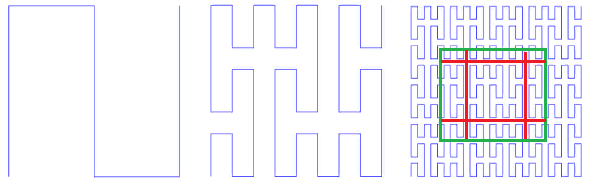


Fig. 9 primeras iteraciones de la curva de Peano

En la esquina inferior izquierda está el comienzo del área de definición (y el valor cero de la función), en la esquina superior derecha el final (y 1), cada vez que movemos 1 paso, agregue 1 / (N * N) al valor (siempre que N - grado 3, por supuesto). Como resultado, en la esquina superior derecha el valor llega a 1. Si agregamos uno en cada paso, dicha función simplemente numera la red cuadrada secuencialmente, que es lo que queríamos.

Todas las curvas de barrido son similares. En este caso, el simplex es un cuadrado de 3x3. En cada iteración, cada punto del simplex se convierte en el mismo simplex, para garantizar la continuidad, debe recurrir a mapeos (volteos).

La auto - similitud es una cualidad muy importante para nosotros. Da esperanza para el valor logarítmico de la búsqueda. Por ejemplo, para un simplex 3x3, todos los números generados dentro de cada uno de los 9 cuadrados elementales mediante iteraciones de detalles posteriores estarán dentro del mismo rango. Solo porque el número es el camino recorrido desde el principio. Es decir Si divide la extensión en 9 partes, el contenido de cada una de ellas puede obtenerse mediante un índice transversal. Y así sucesivamente, cada uno de los 9 subcuadrados de cada uno de los cuadrados se puede obtener mediante una única consulta en el índice (aunque en un rango más pequeño). Por lo tanto, la extensión de búsqueda se puede dividir en un pequeño número de subconsultas cuadradas, leídas en su totalidad o con filtrado (alrededor del perímetro). La Figura 9 muestra la extensión de búsqueda en verde, dividida por líneas rojas en subconsultas.

Sin embargo, la autosimilitud no hace que la curva de numeración sea automáticamente adecuada para fines de indexación.

• la curva debe llenar la cuadrícula cuadrada. Indexamos los valores en los nodos de la red cuadrada y cada vez que no queremos buscar un nodo adecuado en la red, por ejemplo, uno triangular. Al menos para evitar problemas con el redondeo. Aquí, por ejemplo, tal (Figura 10)
  
  
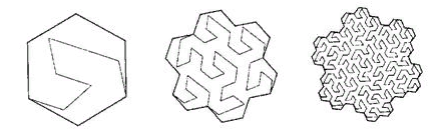
  Figura 10 lago ternario Kokha
  
  La curva no nos conviene. Aunque, perfectamente "une" la superficie.
  
• la curva debe llenar el espacio sin espacios ( dimensión fractal D = 2). Aquí está (Fig. 11):
  
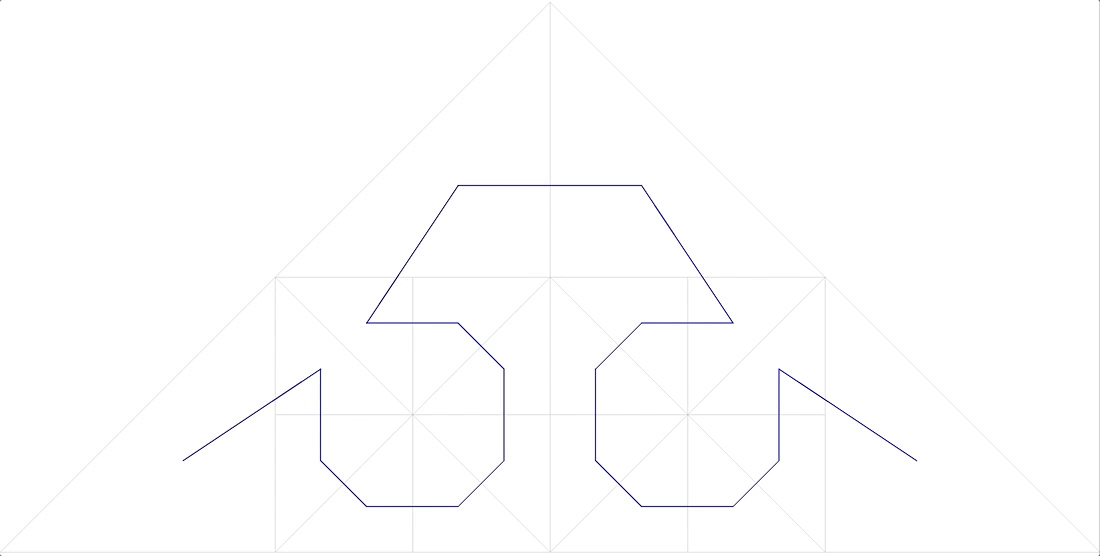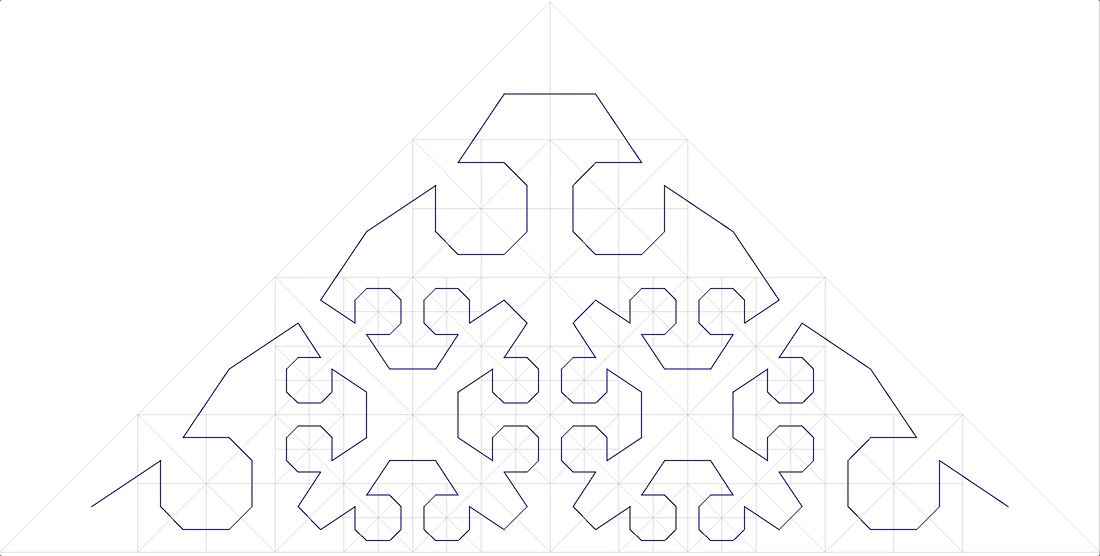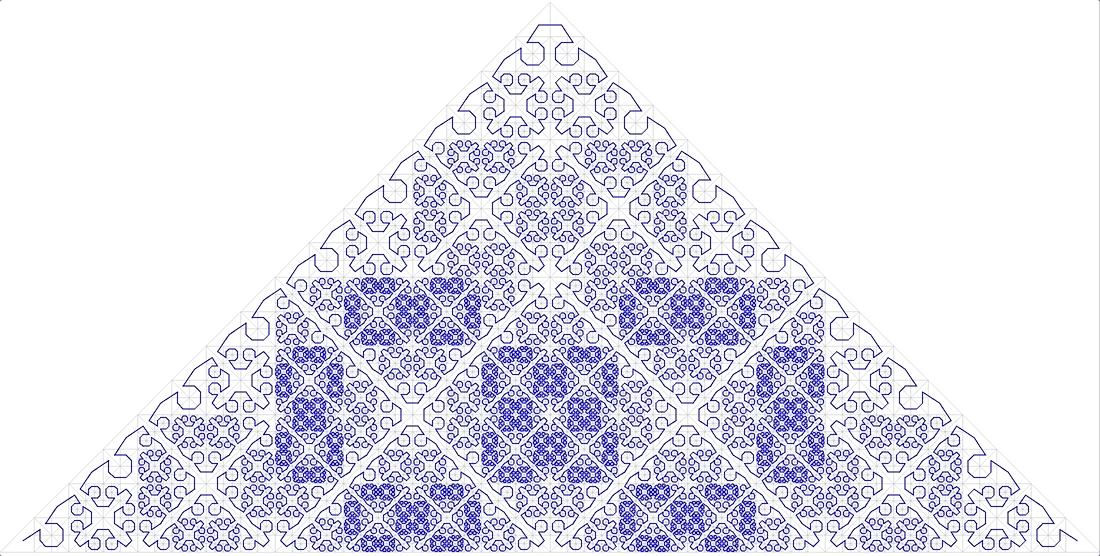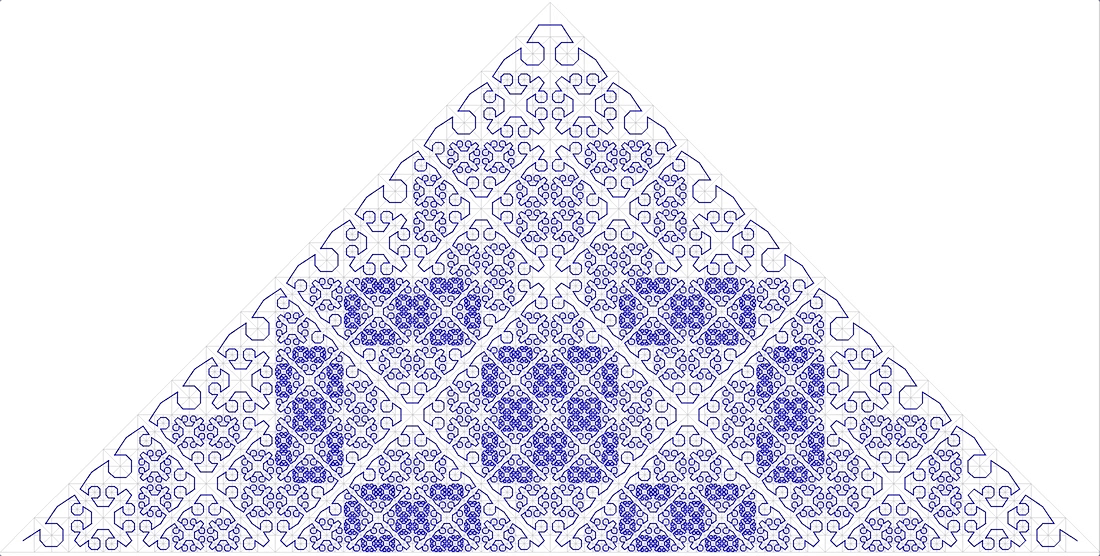
  11 curva fractal anónima
  
  Tampoco encaja.
  
• El valor de la función de numeración (la ruta recorrida a lo largo de la curva desde el principio) debe calcularse fácilmente. De esto se desprende que debido a la ambigüedad que surge, las curvas auto-tocantes no son adecuadas, como la curva de Sierpinski
  
  
  Fig. 12 Curva de Sierpinski
  
  o, que es lo mismo (para nosotros), " pasar el triángulo a lo largo de Cesaro "
  
  
  La figura 13 Triángulo de Cesaro, para mayor claridad, el ángulo recto se reemplaza por 85 °
• no debe haber parámetros en la función de numeración, la curva debe ser uniforme (precisa para la simetría). . : ( )
  
  
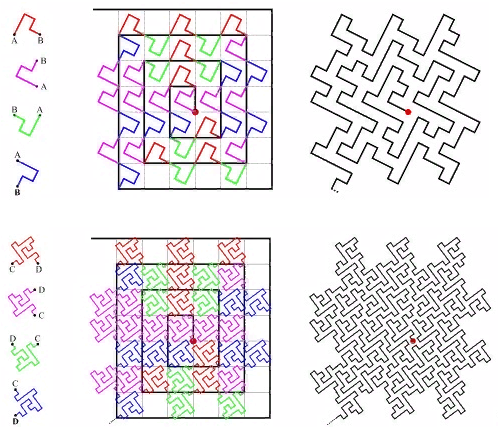
  . 14 “A Plane Filling Curve for the Year 2017”
  
  , ( ) .
  , , , .

La isotropía es otra característica importante. Se entiende que la función de numeración debería ser fácilmente generalizable a dimensiones superiores. Y es bueno si para un cubo N-dimensional todas sus proyecciones de N en las dimensiones (N-1) sean las mismas. Esto se deduce del hecho de que usamos el espacio isotrópico y sería extraño si se usaran diferentes ejes en funciones de manera diferente.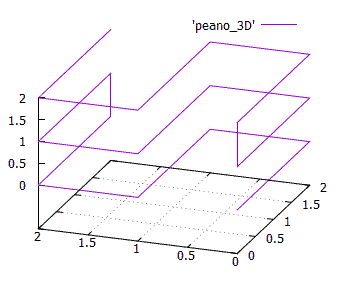


La figura 15 Simplex tridimensional de una curva de Peano de 3x3x3 La

isotropía no es un requisito estricto, pero es un indicador importante de la calidad de una curva de numeración.

En cuanto a la continuidad .

Arriba, vimos ejemplos de funciones de numeración continua que no eran adecuadas para nuestros propósitos. Por otro lado, la función de exploración de línea bastante discontinua con bloques es excelente para esto (con algunas limitaciones). No solo eso, si creamos un índice de bloque basado en el escaneo continuo entrelazado, esto no cambiaría nada en términos de rendimiento. Porque si el bloque se lee en su totalidad, no hay diferencia en el orden en que se recibirán los objetos.

Para curvas auto-similares, esto también es cierto.

• llamemos al tamaño de página, el área de extensión de todos los objetos en la página del disco
  
• el tamaño característico será el área promedio de la página
• ( ) , . , . — . .
• — , .. .
  
• , . , , . , , — () 3...10% () Z-.
  
  — , .

De lo que se ha dicho, se deduce que, a los efectos de la indexación multidimensional, solo se utilizan rectas simples (hipercúbicos) recursivamente tantas veces como sea necesario (para un detalle suficiente de la red).

Sí, hay otras formas auto-similares para tender un puente sobre una red cuadrada, sin embargo, no hay una manera computacionalmente barata de hacer tal transformación, incluido lo contrario. Quizás existan tales trucos numéricos, pero el autor no los conoce. Además, los símplex cuadrados hacen posible dividir efectivamente la extensión de búsqueda en subconsultas por un corte a lo largo de una de las coordenadas . Con un borde roto entre sí, esto es imposible .

¿Por qué los simplexes son cuadrados y no rectangulares? Por razones de isotropía.

Queda por elegir el tamaño y la numeración apropiados dentro del simplex (bypass).

Para elegir el tamaño de un símplex , debe averiguar qué afecta. El número de subconsultas generadas que deberán crearse durante la búsqueda. Por ejemplo, un simplex 3X3 de una curva de Peano se corta en 3 subconsultas con intervalos continuos de números, primero en X, y luego cada uno de ellos en 3 partes en Y. Como resultado, volvemos a la siguiente etapa de la recursión. Si tuviéramos un simplex (entrelazado) 5x5 similar, tendría que ser cortado en 5 partes. O en partes desiguales (ej .: 2 + 3), lo cual es extraño.

Le recuerda a uno de los árboles de búsqueda de alguna manera: por supuesto, puede usar árboles de 5 decimales y 7 decimales, pero en la práctica solo se usan los binarios. Árboles de la trinidadtienen su propio nicho estrecho para buscar por prefijo. Y esto no es exactamente lo que se entiende intuitivamente como árboles ternarios.

Esto se explica por la eficiencia. En un nodo ternario, para seleccionar un descendiente, uno tendría que hacer 2 comparaciones. En un árbol binario, esto corresponde a una elección entre 4 opciones. Incluso profundidades de árbol más cortas no bloquean la pérdida de productividad del mayor número de comparaciones.

Además, si 3X3 fuera más efectivo que 2X2 simplemente porque 3> 2, 4X4 sería más efectivo que 3X3 y 8X8 más efectivo que 5X5. Siempre puede encontrar la potencia adecuada de dos, que está formada por varias iteraciones de 2X2 ...

¿Y qué se ve afectado por el bypass simplex ? En primer lugar, el número de subconsultas generadas por la búsqueda. Porquees bueno si el simplex te permite cortarte en pedazos con intervalos continuos de números. Aquí Peano 3X3 lo permite, por lo que una iteración lo corta en 3 partes. Y si toma un 8x8 simplex con un caballero de ajedrez (Fig. 16), la única opción es tener inmediatamente 64 elementos.


La figura 16 Una de las opciones para eludir el simplex 8x8

Entonces, como descubrimos que el simplex óptimo es 2x2, debemos considerar qué opciones existen para él.


La figura 17 Opciones para eludir un simplex 2x2

Hay tres de ellos, hasta la simetría, llamados condicionalmente “Z”, “omega” y “alfa”.
Inmediatamente llama la atención que "alfa" se cruza a sí mismo y, por lo tanto, no es adecuado para la división binaria. Tendría que cortarse inmediatamente en 4 partes. O 256 en el caso de 8 dimensiones.

La capacidad de utilizar un algoritmo único para espacios de diferentes dimensiones (de los que estamos privados en el caso de una curva como "alfa") parece muy atractiva. Por lo tanto, en el futuro consideraremos solo las dos primeras opciones.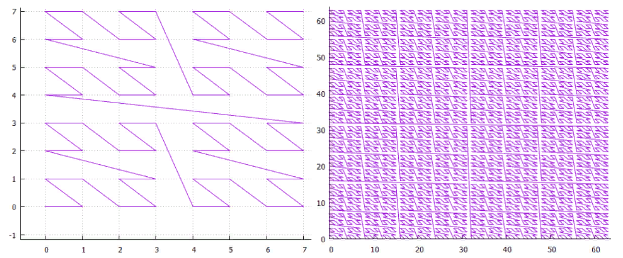


La figura 18 curva Z de la


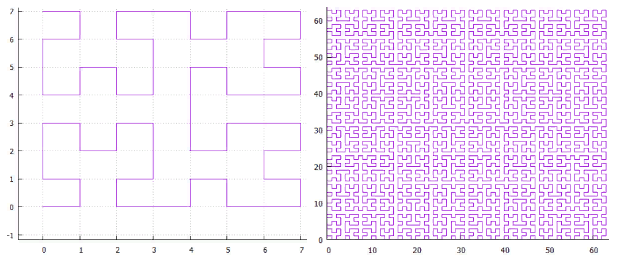fig. 19 “omega”: curva de Hilbert

Una vez que estas curvas tienen un parentesco cercano, pueden procesarse con un algoritmo. La especificidad principal de la curva se localiza en la división de la subconsulta.

• primero encontramos la extensión de inicio, este es el rectángulo mínimo que incluye la extensión de búsqueda y contiene un intervalo continuo de valores clave.
  Se encuentra de la siguiente manera:
  
  • calcular los valores clave para los puntos inferior izquierdo y superior derecho de la extensión de búsqueda (KMin, KMax)
    
  • ( ) KMin, KMax
    
  • , SMin, , SMax
    
  • . , , SMin, . .
  • , , ( ).
    
  • Z- . z- — , — ( ). , , .
• • , , . ,
  • , . — “ ” >= “ ” () , “ ”
    
    
    • “ ” > , ,
      
    • , ,
      
    • “ ” > , , ,
    • caso separado "última clave" == valor máximo de la subconsulta actual, procesada por separado por desplazamiento hacia adelante
      
  • dividir la subconsulta actual
    • agregue 0 y 1 a su prefijo - obtenemos dos nuevos prefijos
    • complete el resto de la clave 0 o 1: obtenemos los valores mínimo y máximo de nuevas subconsultas
    • Los empujamos a la pila, primero el que complementó 1, luego 0. Esto es para la lectura unidireccional del índice.
  
  

En una curva Z, funciona así:


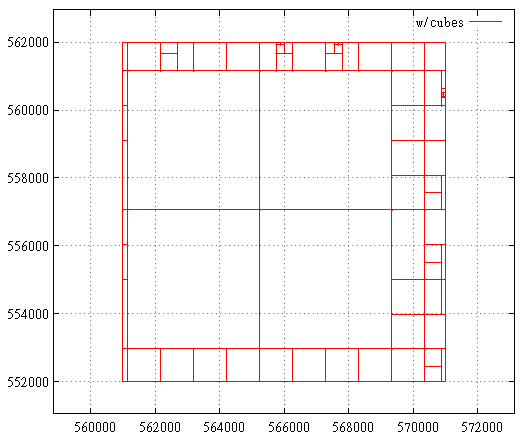La figura 20 - división de subconsulta en caso de curva Z


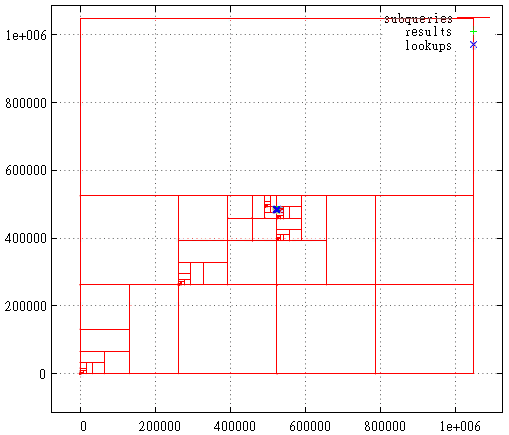La figura 21 Curva de Hilbert, el caso cuando la extensión inicial es la máxima

Aquí se muestra la primera etapa: cortar el exceso de capa de la extensión máxima.


La figura 22 Curva de Hilbert, área de consulta de búsqueda

Y aquí hay un desglose en subconsultas, puntos encontrados y llamadas de índice en el área de consulta de búsqueda. Esta sigue siendo una solicitud muy infructuosa desde el punto de vista de la curva de Hilbert. Por lo general, todo es mucho menos sangriento.

Sin embargo, las estadísticas de consulta dicen que (aproximadamente) en los mismos datos, un índice bidimensional basado en una curva de Hilbert lee 5% menos páginas de disco en promedio, pero funciona la mitad más lento. La desaceleración también se debe al hecho de que el cálculo en sí (directo e inverso) de esta curva es mucho más difícil: 2000 relojes de procesador para Hilbert en comparación con 50 para la curva Z.

Al dejar de admitir la curva de Hilbert, el algoritmo podría simplificarse; a primera vista, dicha desaceleración no está justificada. Por otro lado, este es solo un caso bidimensional, por ejemplo, en un espacio de 8 dimensiones o más, las estadísticas pueden brillar con colores completamente nuevos. Este problema aún está pendiente de aclaración.

PD : La curva Z a veces se llama curva de entrelazado de bits debido al algoritmo para calcular el valor: los dígitos de cada coordenada caen en el valor clave a través de uno, que es muy tecnológico. Pero puede, después de todo, intercalar las descargas no individualmente, sino en paquetes de 2.3 ... 8 ... piezas. Ahora, si tomamos 8 bits, en una clave de 32 bits obtenemos un análogo del índice GRID de 4 niveles de MS SQL. Y en un caso extremo, un paquete de 32 bits cada uno, un algoritmo de escaneo horizontal.

Tal índice (no minúscula, por supuesto) puede ser muy efectivo, incluso más eficiente que la curva Z en algunos conjuntos de datos. Lamentablemente, debido a la pérdida de generalidad.

PPS : el índice descrito es muy similar a trabajar con un árbol cuádruple. La extensión máxima es la página raíz del árbol cuádruple, tiene 4 descendientes ... Y, por lo tanto, el algoritmo se puede atribuir a "métodos de acceso directo".

Las diferencias siguen siendo fundamentales.

El árbol cuádruple no se almacena en ningún lado, es virtual, incrustado en la naturaleza misma de los números. No hay restricciones en la profundidad del árbol; obtenemos información sobre la población de descendientes de la población del árbol principal. Además, el árbol principal se lee una vez, pasamos del más pequeño al más antiguo. Es divertido, pero la estructura física del árbol B permite evitar consultas vacías y limitar la profundidad de recursión.

Una cosa más, en cada iteración solo aparecen dos descendientes, a partir de ellos se pueden generar 4 subconsultas, y no se pueden generar si no hay datos debajo de ellas. En el caso tridimensional, hablaríamos de 8 descendientes, en el caso de 8 dimensiones, aproximadamente 256.

PPPS : al comienzo de este artículo, hablamos sobre la dicotomía al buscar en un índice multidimensional, para obtener el valor logarítmico, es necesario dividir algún recurso finito en cualquier iteración, ya sea el espacio de valores clave o el espacio de búsqueda. En el algoritmo presentado, esta dicotomía colapsó: compartimos simultáneamente la clave y el espacio.

“Vivo en ambos patios y mis árboles siempre son más altos”. ( C )

PPPPS : Tan pronto como llaman a la curva Z, aquí tiene el orden Z y el intercalado de bits y el código / curva de Morton. También se conoce como la curva de Lebesgue, por lo que para mantener el equilibrio, el autor tituló el artículo, incluso en honor de Henry Leon Lebesgue .

PPPPPS : en la ilustración del título, la vista del glaciar Fedchenko es simplemente hermosa, y hay suficiente vacío. De hecho, el autor quedó impresionado con la forma en que diferentes ideas y métodos fluyen suavemente entre sí, fusionándose gradualmente en un algoritmo. Así como las muchas fuentes pequeñas de agua que forman la cuenca forman una sola escorrentía.