Los matemáticos han demostrado que un proceso aleatorio cuando se aplica a una superficie aleatoria invariablemente da lugar a ciertos patrones
En el artículo original, esta es una imagen tridimensional que se puede torcerEn la
película sobre la búsqueda del Arca perdida, Indiana Jones tuvo que buscar una habitación secreta que ocultara el legendario
Arca del Pacto . Para determinar su ubicación exacta, Indiana necesitaba encontrar un mapa especial, visible solo cuando el sol brilla a través de un cristal especial en una habitación determinada en un momento determinado del día.
Una idea similar, que la información más importante puede ser revelada solo con la coincidencia exacta de ciertas circunstancias, se encuentra en muchos mitos. Ocurre en matemáticas, a veces en situaciones inesperadas. Ahora,
tres matemáticos han demostrado que si un cierto tipo de aleatoriedad se ajusta con mucha precisión, aparecen intrincadas figuras geométricas, como un mapa con un tesoro en un piso ordinario.
Estas piezas son como celdas de ajedrez dispersas sobre cuadrículas, que a su vez son creadas por un proceso aleatorio. Uno pensaría que al acumular aleatoriedad en aleatoriedad, obtenemos confusión. Resulta que, como en el caso de los copos de nieve, cuando cada uno de ellos es único, pero al mismo tiempo todos son copos de nieve, el desorden converge a una forma universal, si solo las condiciones resultan ser exactamente las necesarias.
Punto de inflexión
Todos saben que los matemáticos estudian formas. La mayoría de estas formas siguen reglas deterministas: si te doy instrucciones para construir una esfera, recibirás la misma esfera cada vez.
Pero incluso los matemáticos estudian las formas obtenidas como resultado de procesos aleatorios, como, por ejemplo,
caminata aleatoria , un camino, cuya dirección de cada paso se elige aleatoriamente. Además de las caminatas aleatorias, existen otros tipos de objetos geométricos aleatorios, por ejemplo, superficies bidimensionales aleatorias (imagine un paisaje donde las colinas y los valles se dispersan al azar) y mapas aleatorios (un conjunto de puntos aleatorios conectados por líneas).
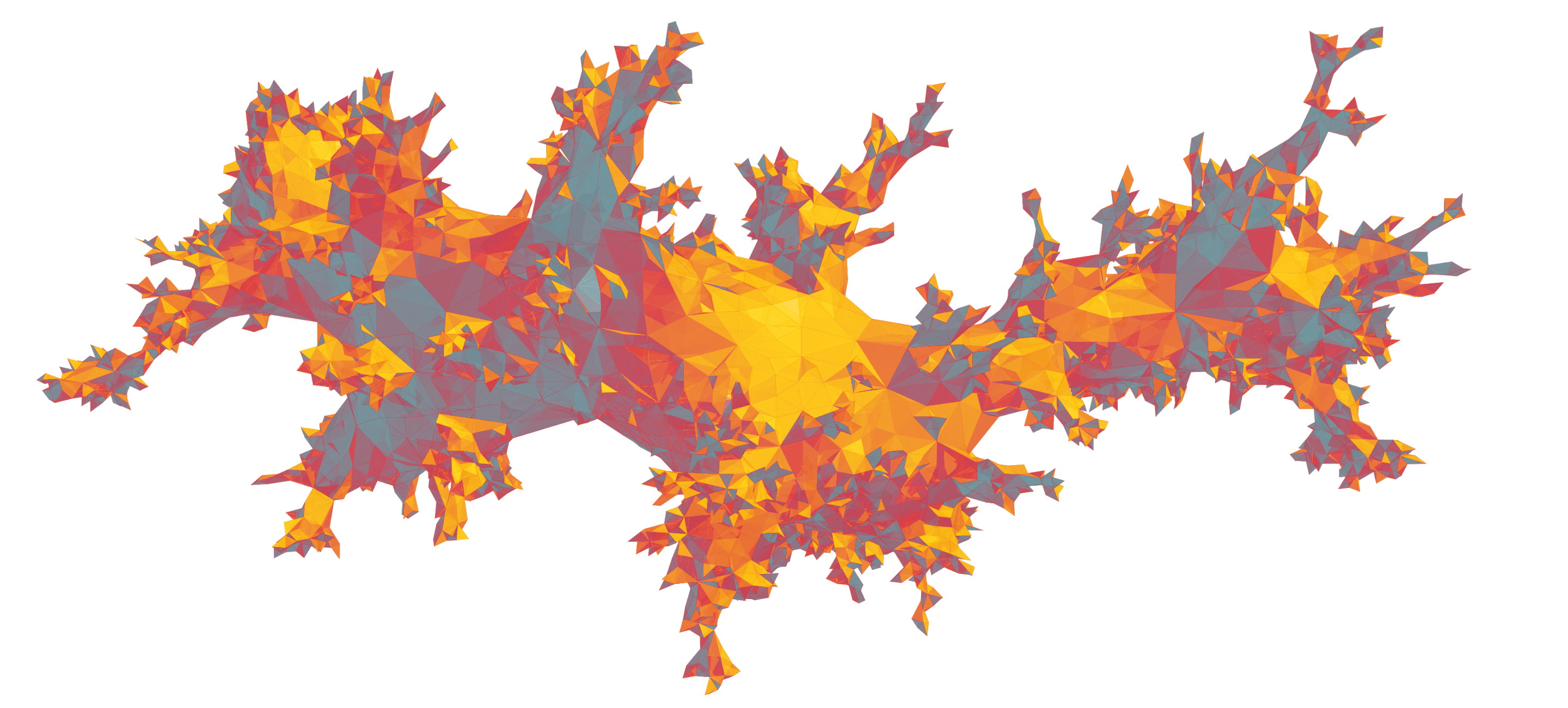Superficie aleatoria obtenida pegando triángulosTodas esas formas son diferentes entre sí. Sin embargo, los matemáticos han descubierto que estos procesos aleatorios convergen a ciertas formas canónicas. Por ejemplo, todas las caminatas aleatorias son una forma de
movimiento browniano con una caminata bastante larga. En los últimos años, los matemáticos han descubierto formas canónicas y otros procesos aleatorios, y recibieron los más altos premios por esto en sus campos.
La nueva evidencia está relacionada con la comprensión de las propiedades subyacentes de otro proceso aleatorio.
Comienza creando una superficie aleatoria. Primero debes pegar los triángulos juntos. Luego, deben combinarse de cualquier manera, solo para que el formulario resultante se cierre, como un paquete en un regalo (no tenía agujeros). Si comienzas con un cierto número de triángulos en tus manos, tendrás muchas oportunidades. Algunas de estas "triangulaciones" producirán superficies casi lisas que se parecen a una pelota. La mayoría de ellos se verán más ásperos, como superficies extremas que se asemejan a cadenas montañosas.
"No se verá como una esfera regular, tendrá picos tan grandes", dijo
Olivier Bernardi , matemático de la Universidad de Brandeis, coautor del trabajo, que también involucró a
Nicholas Curien de la Universidad de París-Sur XI y
Gregory Mjermont de la Escuela Normal Superior en Lyon
Olivier Bernardi, Nicholas Curien y Gregory MyermontMyermont y otro matemático,
Jean-Francois le Gall , establecieron muchas propiedades de estas triangulaciones aleatorias en su trabajo anterior. La nueva prueba va más allá al agregar una segunda capa de aleatoriedad sobre la triangulación aleatoria.
Para agregar una nueva aleatoriedad, marque cada punto en el que los triángulos se encuentran en las esquinas, lo que los matemáticos llaman vértice. Colorea los vértices al azar en blanco o negro. Puede hacerlo lanzando una moneda, aunque la moneda puede no ser completamente honesta y superar a un lado.
Después de pintar los picos, puede hacer varias preguntas sobre el patrón que creó. Uno de los básicos: ¿hasta dónde puede llegar a lo largo de la superficie usando solo un vértice negro? El proceso de moverse a lo largo de vértices conectados del mismo color se llama filtración. Esta es una forma matemática de estudiar un fenómeno físico del mismo nombre cuando un fluido pasa a través de un medio poroso.
Será fácil infiltrarse (o no), dependiendo de cómo se distribuya el peso de la moneda: si la moneda tiende a emitir vértices negros, la infiltración está casi garantizada; si se trata de la extradición de blancos, la filtración seguramente será imposible.
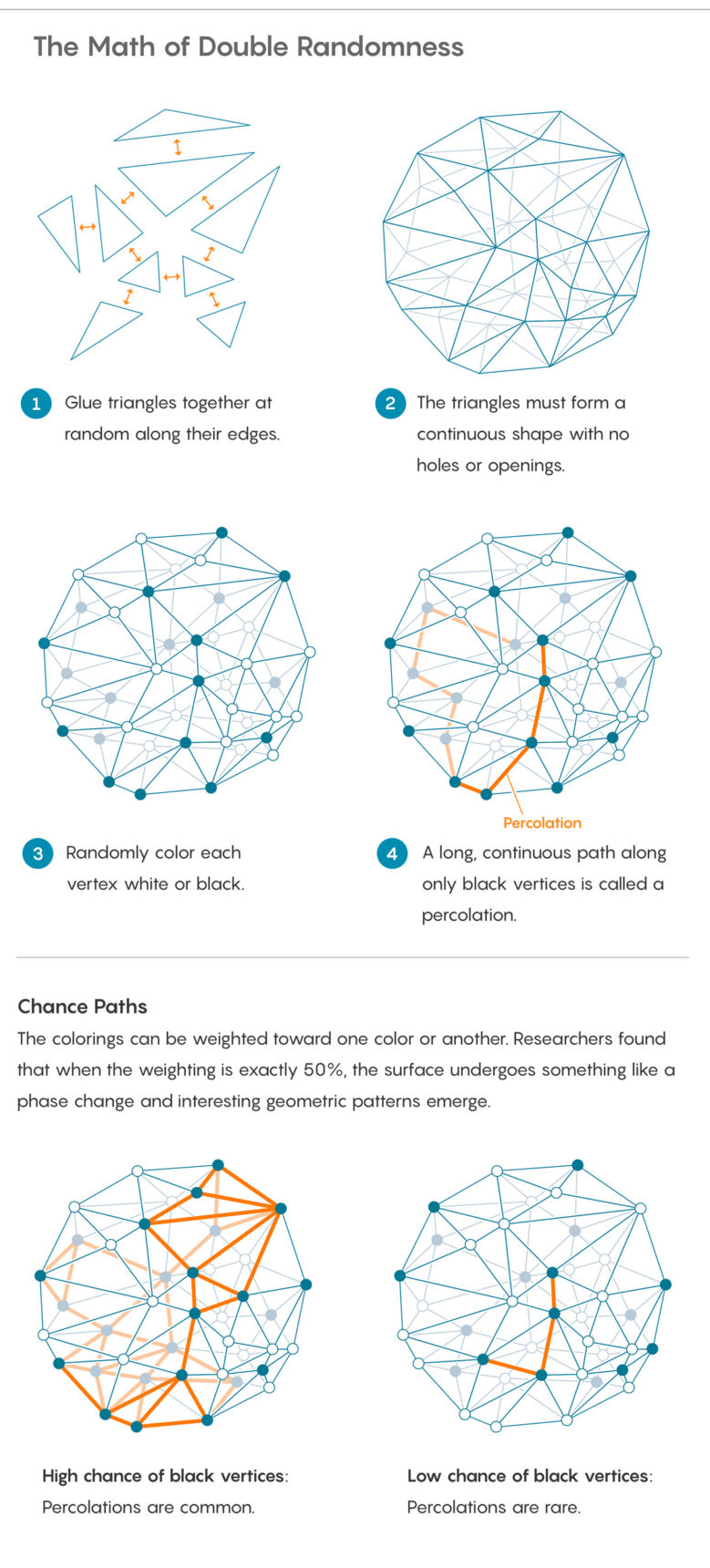
Bernardi, Curien y Myermont estudian casos que se encuentran entre estos extremos: un punto de inflexión en el cambio en el peso de la moneda, cuando la fuga pasa del fenómeno casi imposible al casi garantizado. Ellos llaman a este punto un "umbral crítico". Este es un ejemplo de transición de fase, ese momento mágico en el que el agua caliente de repente se convierte en vapor.
"El umbral crítico significa que si cambio ligeramente mis parámetros, entonces el comportamiento de mi sistema cambiará de dramático a dramático con un signo diferente", dijo Curien.
Los físicos están interesados en las transiciones de fase porque muchos de los fenómenos naturales más importantes ocurren justo al borde. Los matemáticos también están interesados en las transiciones de fase, ya que las propiedades matemáticas importantes a menudo aparecen solo en estos puntos.
"Sabemos que el agua hierve a 100 grados, creando todos estos patrones locos y formas de vapor", dijo
Scott Sheffield , matemático del MIT. “A veces, este comportamiento loco y salvaje se vuelve muy interesante. Esta transición de fase nos llama a entenderlo ”.
En el nuevo trabajo, tres matemáticos prueban que tal comportamiento loco se manifiesta precisamente en la transición de fase de la fuga. Muestran que en este umbral crítico aparece una forma geométrica: única y al mismo tiempo universal.
Orden oculto en el azar
La primera parte del trabajo determina cómo corregir una moneda para que la coloración de los vértices caiga en el umbral entre la presencia y la ausencia de filtración. Confirmando la intuición, prueban que la moneda ideal es el valor crítico, que ofrece un 50% de posibilidades de caer en negro y 50% de caer en blanco.
“Esta es la primera parte del trabajo. Estamos demostrando que exactamente la mitad sucede algo interesante ”, dijo Bernardi.
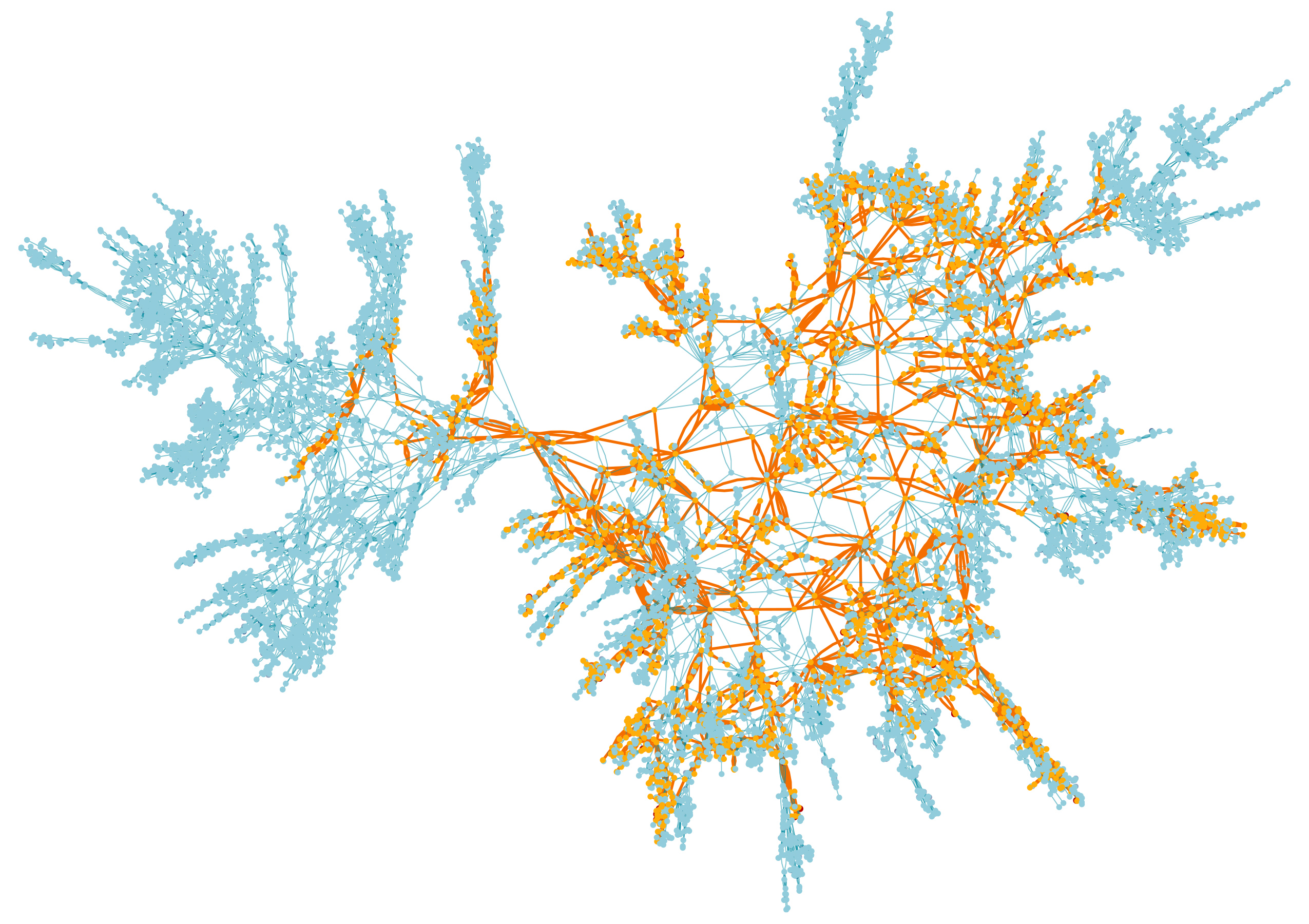Mapa de picos de una superficie aleatoria, el grupo más grande está marcado en naranjaEn la segunda parte, estudiamos lo que sucede allí. Coloreando los vértices en blanco y negro con una moneda justa, obtienes un buen equilibrio entre grupos de vértices en blanco y negro. Los racimos crecen uno alrededor del otro, como matorrales de malezas que compiten por un lugar en un jardín cubierto de vegetación, creando formas geométricas complejas que no aparecen cuando una de las flores domina entre los picos.
"Al elegir un parámetro crítico, descubres grandes grupos", dijo Sheffield. "Sin embargo, no manchan todo el asunto, y no son pequeños".
Dado que la superficie se creó al azar, y el proceso de colorear los vértices también es aleatorio, el grupo grande en una superficie siempre diferirá del grupo grande en la otra. Pero los matemáticos han demostrado que para todas las superficies y todas las formas posibles de colorear sus vértices, los grupos más grandes tendrán las mismas propiedades. Lo primero que probaron es la distribución de probabilidad exacta de los tamaños de los grupos negros más grandes sobre todas las superficies. Descubrieron que con mayor frecuencia se produce un grupo de cierto tamaño intermedio, y que la frecuencia con la que aparecen grupos más grandes o más pequeños aumenta exponencialmente con la distancia desde este intermedio.
También sostienen que todos los grupos grandes pueden reducirse a la misma forma canónica, conocida como el "mapa estable". El mapa estable se refiere a estos grupos de la misma manera que el movimiento browniano para caminar al azar. Esto significa que si los grupos individuales están ligeramente separados, de modo que cada paso aleatorio dentro del grupo sea menos notable en la geometría de la figura completa como un todo, entonces los grupos gradualmente llegarán a una forma común. Parecen copos de nieve: parecen únicos en la vecindad, pero su comunidad es claramente visible desde lejos.
"Encontraron este mapa estable, el límite natural de escala", dijo Sheffield.
El trabajo amplía los límites del conocimiento sobre formas y procesos aleatorios acumulados por los matemáticos en los últimos años. También nos revela que es precisamente en ese momento cuando el sistema aleatorio parece más caótico que un orden geométrico excepcional comienza a verse a través de él.