Hay dos hombres llamados "Van Eck". El primero, en 1985, mostró al mundo cómo interceptar datos de un monitor (
Van Eck phreaking ) por $ 15, el segundo, en 2010, ideó una secuencia astuta (secuencia de
Van Eck ). Más empinada que la simplicidad de la tarea de esta secuencia solo pueden ser sus propiedades y rompecabezas.
Entonces, el algoritmo para generar miembros de secuencia. Tomamos el "número inicial", por ejemplo, "0", escribimos. El siguiente término es cuántos pasos atrás se produjo este número en la subsecuencia anterior. Si nunca, entonces escribe cero. El siguiente es cuántos pasos atrás hubo cero en la subsecuencia anterior, es decir, un paso atrás. Escribimos la unidad. Unidad uno: escriba cero. Vaya, cero se encontró con dos pasos atrás. Escribimos dos, y así sucesivamente ...
Para el punto de informe "0", los primeros 97 miembros de la secuencia:
0, 0, 1, 0, 2, 0, 2, 2, 1, 6, 0, 5, 0, 2, 6, 5, 4, 0, 5, 3, 0, 3, 2, 9, 0, 4, 9, 3, 6, 14, 0, 6, 3, 5, 15, 0, 5, 3, 5, 2, 17, 0, 6, 11, 0, 3, 8, 0, 3, 3, 1, 42, 0, 5, 15, 20, 0, 4, 32, 0, 3, 11, 18, 0, 4, 7, 0, 3, 7, 3, 2, 31, 0, 6, 31, 3, 6, 3, 2, 8, 33, 0, 9, 56, 0, 3, 8, 7, 19, 0, 5, 37, 0, 3, 8, 8, 1
Tabla:
Aún más línea de tiempo:
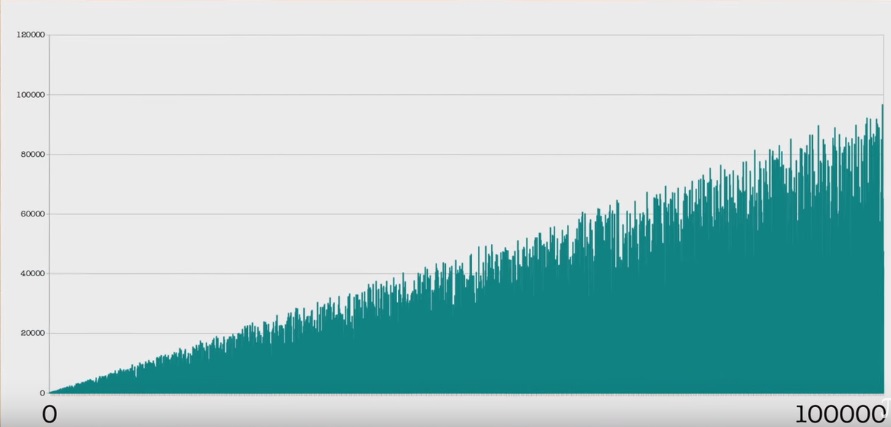
Las propiedades de una secuencia se prueban con bastante facilidad que su término máximo aumenta todo el tiempo y que tiene un número infinito de ceros. O que no hay períodos en él. (Algunos teoremas y consecuencias
aquí .)
Gráfico logarítmico:
Programa en Python:
A181391 = [0] last_pos = {} for i in range(10**4): new_value = i - last_pos.get(A181391[i], i) A181391.append(new_value) last_pos[A181391[i]] = i
Para el número inicial "1", el primer centenar es:
1, 0, 0, 1, 3, 0, 3, 2, 0, 3, 3, 1, 8, 0, 5, 0, 2, 9, 0, 3, 9, 3, 2, 6, 0, 6, 2, 4, 0, 4, 2, 4, 2, 2, 1, 23, 0, 8, 25, 0, 3, 19, 0, 3, 3, 1, 11, 0, 5, 34, 0, 3, 7, 0, 3, 3, 1, 11, 11, 1, 3, 5, 13, 0, 10, 0, 2, 33, 0, 3, 9, 50, 0, 4, 42, 0, 3, 7, 25, 40, 0, 5, 20, 0, 3, 8, 48, 0, 4, 15
Tabla:
Para el número inicial "2", el primer centenar es:
2, 0, 0, 1, 0, 2, 5, 0, 3, 0, 2, 5, 5, 1, 10, 0, 6, 0, 2, 8, 0, 3, 13, 0, 3, 3, 1, 13, 5, 16, 0, 7, 0, 2, 15, 0, 3, 11, 0, 3, 3, 1, 15, 8, 24, 0, 7, 15, 5, 20, 0, 5, 3, 12, 0, 4, 0, 2, 24, 14, 0, 4, 6, 46, 0, 4, 4, 1, 26, 0, 5, 19, 0, 3, 21, 0, 3, 3, 1, 11, 42, 0, 6, 20, 34, 0, 4, 20, 4
Tabla:
Fuentes