¿Qué debe hacer si necesita dibujar un gráfico, pero las herramientas que vienen debajo de su brazo dibujan una especie de bulto de cabello o incluso devoran toda la RAM y cuelgan el sistema? En los últimos años de trabajo con gráficos grandes (cientos de millones de vértices y bordes), probé muchas herramientas y enfoques, y casi no encontré críticas decentes. Por lo tanto, ahora estoy escribiendo tal crítica yo mismo.
¿Por qué visualizar gráficos en absoluto?
Encuentra qué buscar
En la entrada, generalmente solo tenemos un conjunto de vértices y bordes, que es esencialmente un gráfico. Podemos calcular algunas características estadísticas, métricas gráficas a partir de él, pero esto no le dará una idea clara de lo que es. Una buena visualización puede mostrar si el grupo tiene puentes o puentes, o si es homogéneo o si se fusiona en un solo bulto con algún centro principal de atracción.
Alardear de
La visualización de datos, por definición, resuelve el problema de representación. Si ya se ha realizado algún trabajo, puede mostrar las conclusiones en una imagen espectacular. Por ejemplo, si realizó una agrupación de un gráfico, puede colorear el gráfico en grupos y mostrar cómo se relacionan las diferentes etiquetas entre sí.
Obtener signos
A pesar de que los algoritmos de visualización de gráficos se desarrollaron principalmente solo como herramientas para obtener imágenes, pueden usarse como métodos para reducir la dimensión. El gráfico en sí, si está representado por una matriz de adyacencia, son datos en un espacio de alta dimensión, y al renderizar, obtenemos dos coordenadas para cada vértice (a veces tres o más, pero esto es una excepción). La proximidad de los vértices en la visualización a menudo expresa similitud en las propiedades.
¿Cuál es el problema con los gráficos grandes?
Por gráficos grandes me referiré a dimensiones, digamos, a partir de 10 mil vértices o aristas. Para tamaños más pequeños, generalmente no hay problemas, porque casi todas las herramientas que se pueden encontrar mediante una búsqueda rápida en Internet básicamente resuelven bien sus problemas para tales volúmenes. ¿Qué hay de malo con los gráficos grandes? Dos problemas: esto es legibilidad y velocidad. Se espera que cuantos más objetos, más difícil sea navegarlos. Para gráficos grandes, a menudo se obtienen imágenes que son imposibles de entender. Además, los algoritmos de gráficos son generalmente muy lentos, muchos tienen una complejidad algorítmica proporcional al cuadrado (a veces cubo) del número de vértices y / o bordes. Incluso si espera el renderizado, todavía no puede permitirse pasar por muchas opciones para obtener un resultado satisfactorio.
¿Qué escriben las diferentes personas inteligentes sobre esto?
Hay un par de trabajos que me gustaría llamar la atención:
[1] Helen Gibson, Joe Faith y Paul Vickers: "Una encuesta de técnicas de diseño de gráficos bidimensionales para la visualización de información"Los chicos primero ordenan qué enfoques hay para dibujar gráficos, explican los principios del trabajo y luego intentan probarlos todos. Hay una tabla muy detallada con información sobre diferentes algoritmos, incluida su complejidad algorítmica.
[2] Oh-Hyun Kwon, Tarik Crnovrsanin y Kwan-Liu Ma “¿Cómo sería un gráfico en este diseño? Un enfoque de aprendizaje automático para la visualización de gráficos grandes "Aquí, nuestros camaradas se confundieron mucho y obtuvieron todas las implementaciones de algoritmos de visualización de gráficos que pudieron. Luego visualizaron muchos gráficos y dieron marcadores para el marcado. De acuerdo con los resultados, enseñamos al modelo a evaluar cómo se verá el gráfico en diferentes opciones de estilo. Tomé algunas fotos de este artículo.
Teoría
El apilamiento es una forma de asignar coordenadas a cada vértice de un gráfico. Por lo general, estamos hablando de coordenadas en un plano, aunque en general no tiene que ser un plano. Simplemente usar más de 2 dimensiones casi nunca es necesario.
¿Qué es un buen estilo?

Es muy fácil decir que algo se ve bien o mal, pero es difícil explicarle a la máquina cómo realizar dicha evaluación. Para hacer un estilo “bueno”, las métricas llamadas “estéticas” generalmente se optimizan, y se formulan de manera más objetiva. Aquí hay algunos de ellos:
Cruce mínimo de costillasEs simple: cuando hay muchas intersecciones, resulta "gachas", cuando es pequeño, entonces la imagen se ve "más limpia"
Los picos adyacentes están cerca uno del otro, los no adyacentes están lejos.Un gráfico por definición es un conjunto de conexiones entre vértices y un conjunto de vértices. Acercar los vértices conectados entre sí es una forma directa y lógica de expresar las propiedades básicas de los datos gráficos.
Las comunidades están agrupadasEsto se desprende del párrafo anterior. Si hay muchos nodos que están más conectados entre sí que con el resto del gráfico, forman una "comunidad" y en la imagen deberían verse como un grupo denso
Superposiciones mínimas de vértices y bordes.Bastante obvio. Si no podemos distinguir uno o varios objetos aquí, entonces la visualización se lee mal.
Distribuir vértices y / o bordes de manera uniformeEsta condición es útil si las propiedades del gráfico no permiten distinguir al menos alguna estructura de lo contrario. Por ejemplo, si tenemos el gráfico completo: es un grupo denso, entonces es mejor difuminarlo en la imagen para ver al menos la irregularidad de las conexiones que permitir que se fusione en un punto sólido.
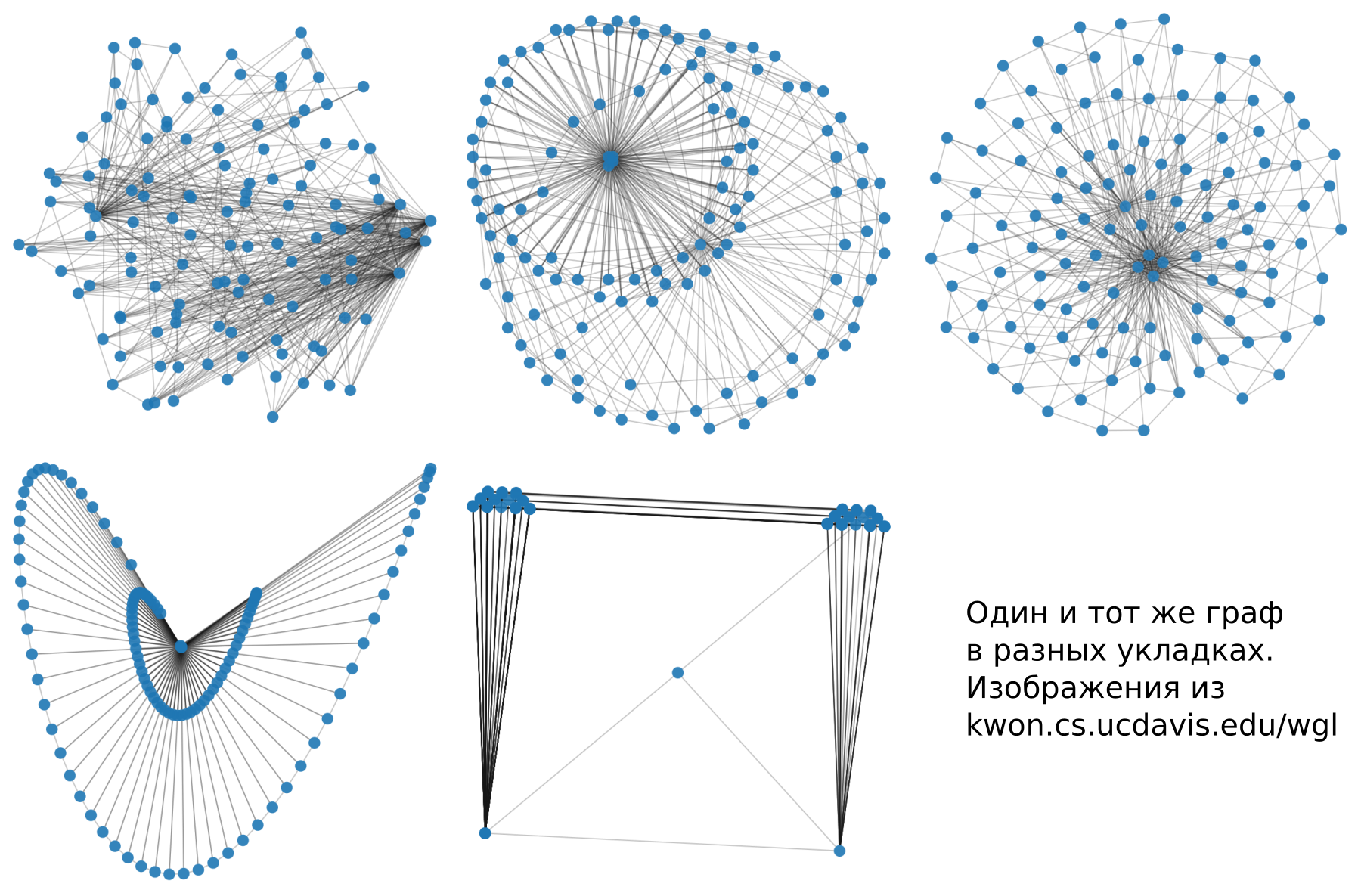
¿Cuáles son los estilos
Considero importante tener en cuenta estos tres tipos de estilo, aunque hay muchas clasificaciones y tipos. Sin embargo, el conocimiento de estos tipos es suficiente para navegar por el tema.
- Dirigido a la fuerza y basado en la energía
- Reducción de dimensiones
- Características del nodo
Dirigido a la fuerza y basado en la energía
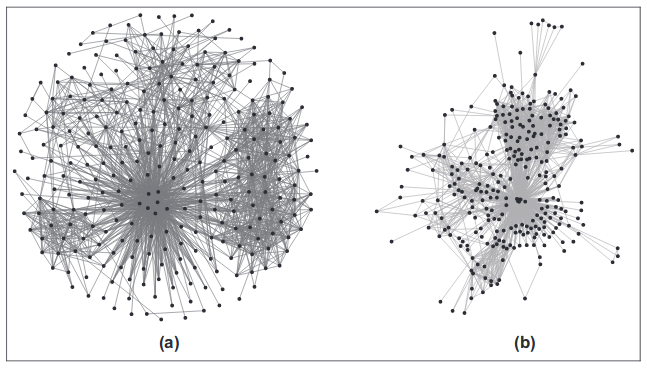
Estos métodos utilizan una simulación de fuerza física. Los picos se representan como partículas cargadas que se repelen entre sí, y los bordes, como cuerdas elásticas que unen los picos adyacentes. Luego, el movimiento de vértices en dicho sistema se simula hasta que se establece un estado estable. Otros enfoques intentan describir la energía potencial de dicho sistema y encontrar la posición de los vértices que corresponderá al mínimo.
Las ventajas de esta familia de algoritmos como imagen. Por lo general, se obtiene un estilo realmente bueno que refleja la topología del gráfico. Contras entre los parámetros que deben configurarse. Bueno y, por supuesto, la complejidad computacional. Para cada vértice, necesitas calcular las fuerzas que actúan desde todos los demás vértices.
Los algoritmos familiares importantes son Force Atlas, Fruchterman-Reingold, Kamada Kawaii y OpenOrd. El último algoritmo utiliza optimizaciones difíciles, por ejemplo, corta bordes largos para acelerar los cálculos y, como efecto secundario, se obtienen grupos más densos de picos cercanos.
Reducción de dimensiones

El gráfico puede definirse por la matriz de adyacencia, es decir, por la matriz cuadrada NxN, donde N es el número de vértices. Esto puede interpretarse como N objetos en un espacio de dimensión N. Esta representación permite el uso de métodos universales de reducción de dimensión, como tSNE, UMAP, PCA, etc. Otro enfoque se basa en calcular las distancias teóricas entre los vértices, en función de los pesos de los bordes y el conocimiento de la topología local, y luego tratar de mantener la relación entre estas distancias al moverse en espacios de menor dimensión.
Diseño basado en características

Por lo general, los datos provienen del mundo real, donde no solo tenemos información sobre la adyacencia de los vértices. Los picos son algunos objetos reales con sus propias propiedades. Recordando esto, podemos usar las propiedades de los vértices para mostrarlos en el plano. Para hacer esto, puede usar cualquier enfoque comúnmente utilizado para datos tabulares. Estos son los métodos para reducir las dimensiones de PCA, UMAP, tSNE, Autoencoders ya mencionados anteriormente. O puede dibujar un diagrama de dispersión simple (diagrama de dispersión) para pares de entidades y dibujar bordes que ya están en la parte superior de la vista resultante. Por separado, podemos mencionar Hive Plot, un método interesante cuando los valores del atributo corresponden a diferentes ejes dirigidos desde el centro, en el que se ubican los vértices, y los bordes se dibujan mediante arcos entre ellos.
Herramientas de visualización de gráficos grandes

A pesar de que la tarea de visualización es antigua y relativamente popular, existen grandes problemas con las herramientas para gráficos grandes. La mayoría de ellos no son compatibles. Casi todos tienen algunas de sus serias deficiencias, que deben ser soportadas. Solo hablaré de aquellos que son dignos de mención y que pueden usarse para gráficos grandes. Para gráficos pequeños, no hay problemas: las herramientas son fáciles de encontrar y básicamente funcionan bien.
GraphViz

Transacciones y direcciones de la cadena de bloques de Bitcoin hasta 2011

Configurar ajustes puede ser difícil
Una herramienta CLI de la vieja escuela con su propio lenguaje de descripción gráfica: punto. De hecho, este es un paquete con un estilo diferente para cualquier ocasión. Para gráficos grandes, hay una herramienta sfdp: pertenece a la clase de apilamiento de Fuerza dirigida. Las ventajas y desventajas de esta herramienta en el lanzamiento desde la línea de comandos. Esto es muy conveniente para la reproducibilidad y la automatización, sin embargo, sin controles deslizantes y mostrando resultados intermedios, la configuración de parámetros se vuelve muy dolorosa. Establecemos los parámetros, comenzamos, esperamos sin una barra de progreso, vemos el resultado, cambiamos los parámetros, reiniciamos. Capaz de escribir en svg, png y otros formatos de imagen.
Gephi
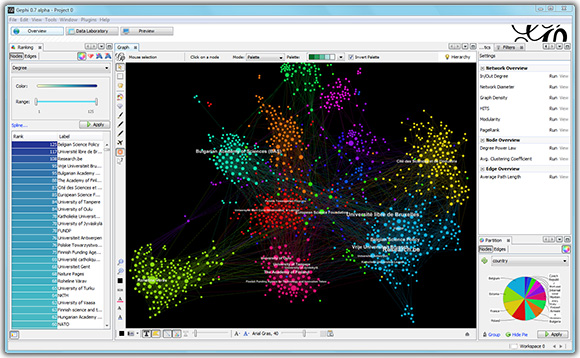

Recomendaciones 173 mil películas con iMDB

Varios millones de picos ya es una tarea demasiado difícil
Quizás la herramienta más poderosa en su totalidad. Esta es una aplicación GUI que contiene un conjunto de estilos básicos, así como muchas otras herramientas de análisis de gráficos. La comunidad gephi ha escrito muchos complementos, como mi Multigravity Force-Atlas 2 favorito o un complemento para exportar estilos a una página web interactiva. Además, la implementación original de OpenOrd está contenida en Gephi. Gephi tiene herramientas para pintar vértices y bordes de acuerdo con sus propiedades, establecer títulos, tamaños y otras opciones de representación. Hay una exportación a los principales formatos de imagen, incluido el vector.
Un hecho muy molesto es que Gephi ha sido abandonada por varios años. Los dos desarrolladores principales, que no tienen los recursos para transferir su conocimiento necesario para un mayor desarrollo a otra persona, dijeron que ya no podían apoyar activamente a Gephi. Otras desventajas incluyen una cierta "capacidad" de la interfaz y la falta de características obvias, pero nada "es simplemente mejor", nadie escribió. Según las últimas noticias, apareció una declaración en el blog del proyecto de que el poder del WebGL moderno ya está por delante del antiguo Gephi y existe la posibilidad de verlo revivir como una aplicación web.
igraph

Gráfico de recomendación de música en lastfm. La fuente está
aquí .
Uno no puede dejar de rendir homenaje a este paquete de propósito general para el análisis gráfico. Una de las visualizaciones gráficas más espectaculares de su tiempo fue realizada por uno de los autores de igraph. Desarrolló su estilo DrL para esto. Era un gráfico de recomendaciones de las bandas de lastfm. El resultado es mayor.
Las desventajas incluyen documentación desagradable. Al menos a la pitón api. Es más fácil leer la fuente de inmediato.
LargeViz
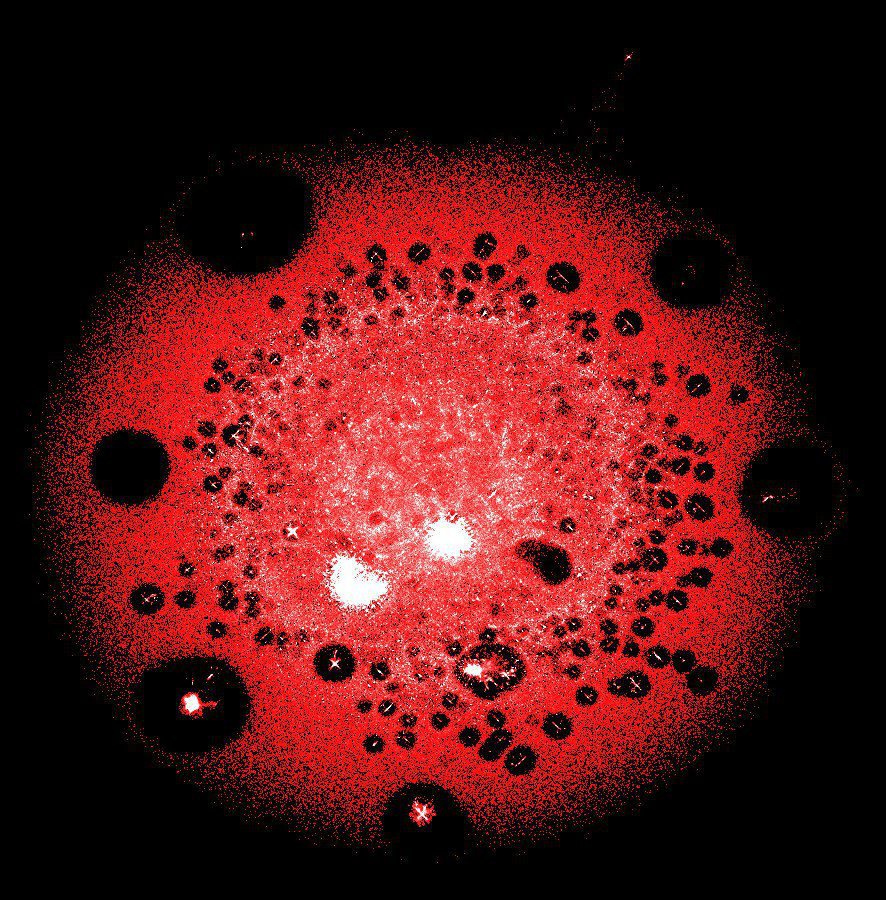
Varias decenas de millones de picos (transacciones y direcciones) en uno de los grupos más grandes de blockchain de Bitcoin
Salvación real cuando necesitas dibujar un gráfico gigante. LargeViz se refiere a algoritmos de reducción de dimensionalidad y puede usarse no solo para gráficos, sino también para datos tabulares arbitrarios. Funciona desde la línea de comandos y tiene un excelente rendimiento. Muy económico en memoria y rápido.
Grafismo

Direcciones pirateables en una semana y sus transacciones

Interfaz clara pero muy limitada, configuración predeterminada razonable
La única herramienta comercial en esta lista. Graphistry es un servicio que toma sus datos y realiza cálculos pesados de su lado. El cliente solo mira la hermosa imagen en el navegador. De hecho, gephi no es mejor que las opciones predeterminadas razonables y la interactividad. Implementa solo un estilo: algo similar a ForceAtlas. Hay un límite de 800 mil para el número máximo de vértices o aristas.
Incrustaciones de gráficos
Para tamaños locos, también hay un enfoque. Ya comenzando con un millón de vértices, al dibujar, tiene sentido mirar solo la densidad de los vértices en diferentes puntos del espacio, simplemente porque no se puede ver nada más. La mayoría de los algoritmos inventados específicamente para representar gráficos funcionarán para decenas de millones de vértices o bordes durante muchas horas, si no días. Puede salir de esta situación resolviendo un problema ligeramente diferente. Existen muchos métodos para obtener representaciones vectoriales de una dimensión dada, que reflejan las propiedades de los vértices del gráfico. Después de recibir tales representaciones, solo queda reducir la dimensión a 2 para obtener la imagen ya.
Node2Vec

Nodo2Vec + UMAP
Adaptación de word2vec regular para gráficos. En lugar de secuencias de palabras, las secuencias de vértices se toman para un recorrido aleatorio del gráfico y se envían a word2vec en lugar de palabras. El método solo tiene en cuenta la información sobre la vecindad de los vértices. Esto suele ser suficiente.
Verso
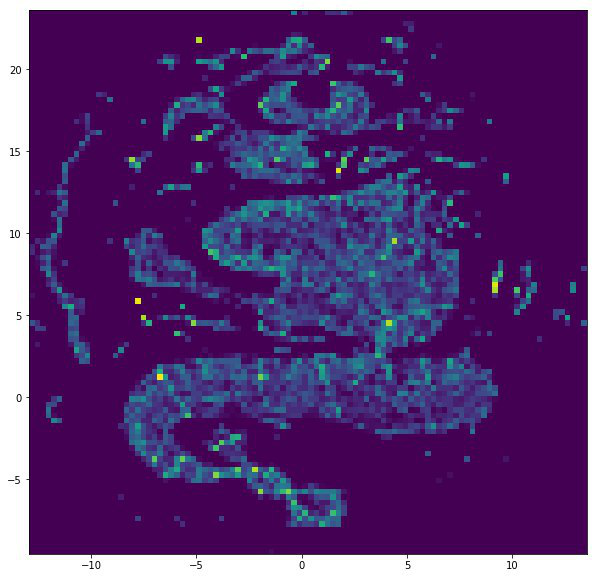
VERSO + UMAP
Un algoritmo avanzado para obtener incrustaciones de gráficos, que busca obtener una representación versátil para los vértices, es decir, tener en cuenta todas las funciones que desempeña un vértice en un gráfico. Se tiene en cuenta la vecindad de los vértices y la topología local del gráfico.
Convoluciones gráficas

Convoluciones Gráficas + Autoencoder
Hay muchas formas de determinar la operación de convolución en los gráficos, pero en esencia es una "mancha" de información en el gráfico, de modo que los vértices reciben información sobre los signos de sus vecinos. Puede agregar información de topología local a estos atributos.
Bonificación: un poco más sobre convolución gráfica
Todos los enfoques descritos se basan en algunas herramientas listas para usar. El último caso es una excepción. Para implementar la convolución gráfica, debe pensar un poco y escribir un poco de código.
Un análisis detallado de las convoluciones en gráficos y otros datos no euclidianos es un tema digno de un artículo separado. Aquí describiré el enfoque básico más simple, que no requiere marcos de gráficos especiales y es fácilmente escalable. Entonces, queremos que los signos de cada vértice del gráfico contengan información sobre los signos de los vecinos.
¿Cómo hacemos esto?
La forma más obvia es simplemente tomar el promedio de los vecinos. Si piensa un poco más sobre lo que sucede y qué información pierde el promedio, puede agregar otras estadísticas allí, como desviación estándar, mínimo, máximo, etc.
¿Cómo organizarlo ahora? Para empezar, un gráfico es esencialmente muchos vértices y muchos bordes. Solo nos interesan las piezas conectadas de más de un vértice, por lo que la lista de aristas en nuestro caso define completamente el gráfico. Esto se escribe convenientemente en forma de tabla: en la primera columna, los vértices de los que sale el borde, en la segunda, donde entran estos bordes. Luego necesitamos leer las estadísticas. Esta es una tarea muy común y, por lo tanto, puede usar marcos en los que todo esté optimizado para nosotros.
El poder de los marcos de tablas en el análisis gráfico
Hemos llegado a la conclusión de que tenemos una placa que especifica un gráfico y necesitamos leer estadísticas para algunas cantidades. Tablas y estadísticas: todo esto está en pandas, por lo que lo siguiente será un ejemplo de implementación en él.
Para comenzar, establezcamos el gráfico:
ara = np.arange(101).reshape(-1, 1) sample = np.vstack((np.hstack((ara[:-1], ara[1:])),
Esto es solo una cadena de 101 vértices conectados uno tras otro, como en la figura.

Luego establecemos los signos de los vértices al azar:
feats = np.random.normal(size=(101, 10))
Y haremos marcos de datos de pandas a partir de todo esto:
edges = pd.DataFrame(sample, columns=['source', 'target']) cols = ['col{}'.format(i) for i in range(10)] feats = pd.DataFrame(feats, columns=cols) feats['target'] = ara
Ahora establecemos la función de convolución en sí:
def make_conv(edges, feats, cols, by, on, size=1000000, agg_f='mean', prefix='mean_'): """ edges -- edgelist: pandas dataframe with two columns (arguments by and on) feats -- features dataframe with key column (argument on) and features columns (argument cols) by -- column in edges to be used as source nodes on -- column in edges to be used as neighbor nodes size -- number of unique source nodes to be used in one chunk agg_f -- can be interpreted as pooling function. Pandas has several optimised functions for basic statistics, that can be passed as string arg (see pandas docs), but you also can provide any function you like prefix -- prefix for new column names """ res_feats = []
Que esta pasando aqui
Primero, seleccionamos un pedazo de vértices para el cual haremos una convolución, tomaremos todos sus bordes, lo concatenaremos con los signos de los vecinos y lo escribiremos en el marco de datos temporales. Luego agrupamos por los vértices de las fuentes, y agregamos usando la función agg_f, que es simplemente promedio por defecto. Agregue el resultado de la pieza actual a la lista, y al final solo concatene los resultados.

Para este gráfico, se verá así
Aplicamos la función y dibujamos el resultado:
conv1 = make_conv(edges, feats, cols, 'source', 'target') plt.figure(figsize=(3, 8)) plt.imshow(np.hstack((feats[cols].values, conv1.values[:, 1:])), cmap='jet');

Los signos iniciales, luego el original y el resultado de la primera convolución, luego el original y el resultado de dos convoluciones.
Por ejemplo, se eligió un caso tan simple que fue fácil ver visualmente cómo los signos están "manchados" en los vecinos si dibuja directamente una matriz de signos. En un caso más general, el proceso se ve así:

Si quieres un poco más de matemática
Si ya ha escuchado sobre convoluciones gráficas, lo más probable es que fuera en el contexto de redes de convolución gráfica (Redes Convolucionales Gráficas - GCN). Para algunos, los trucos con las tabletas que se describen aquí pueden parecer "no difíciles". De hecho, un artículo muy interesante está dedicado al uso de convoluciones gráficas sin aprendizaje profundo: "Simplificación de redes convolucionales gráficas". Da tal definición de convolución
donde
Es una matriz de características, y
Es el laplaciano normalizado del gráfico, que se define así:
aqui
Es la matriz de adyacencia del gráfico sumada con la matriz de identidad, y
- la matriz en la diagonal de la cual se registran los grados de los vértices del gráfico. Y todo esto está escrito en un par de líneas en python usando scipy y numpy:
S = sparse.csgraph.laplacian(adj, normed=True) feats_conv = S @ feats
Aquí, sparse es el módulo dentro de scipy para trabajar con matrices dispersas, adj es la matriz de adyacencia, y feats y feats_conv son los signos antes y después de la convolución. Este enfoque es más riguroso, pero muy escaso. Además, si piensa un poco sobre el significado de lo que está sucediendo, esto es equivalente a la diferencia entre el valor de la característica en el vértice y el promedio en los vecinos del vértice, es decir, puede resolverse completamente mediante el esquema anterior con tablas, si agrega una operación.
Referencias
Revisiones de visualización de gráficosleonidzhukov.net/hse/2018/sna/papers/gibson2013arxiv.org/pdf/1710.04328.pdfSimplificación de redes convolucionales gráficasarxiv.org/pdf/1902.07153.pdfGraphVizgraphviz.orgGephigephi.orgigraphigraph.orgLargeVizarxiv.org/abs/1602.00370github.com/lferry007/LargeVisGrafismowww.graphistry.comNode2Vecsnap.stanford.edu/node2vecgithub.com/xgfs/node2vec-cVersotsitsul.in/publications/versegithub.com/xgfs/verseCuaderno con código de paquete completo de pandasgithub.com/iggisv9t/graph-stuff/blob/master/Universal%20Convolver%20Example.ipynbConvoluciones gráficasAquí hay trabajos recopilados en redes de convolución de gráficos:
github.com/thunlp/GNNPapersLa esencia de todo el artículo en una tabla.