La representación de límites (B-rep) es el método principal para representar objetos modelados en la mayoría de los núcleos geométricos, incluido nuestro núcleo C3D Modeler. Los algoritmos centrales que editan modelos, como la aplicación de operaciones de filete, la realización de operaciones de corte y la obtención de proyecciones planas requieren la precisión de las representaciones B-rep. La creciente variedad de datos 3D en formatos poligonales hace que la tarea de transformación de modelos de polígonos en representación de límites sea cada vez más relevante. Como resultado, desarrollamos un nuevo SDK, C3D B-Shaper, que forma parte de nuestro kit de herramientas C3D.



Usar un algoritmo de triangulación (conocido como teselación) en la representación de límites de un modelo es relativamente fácil. Construir representaciones poligonales (teseladas) es útil para fines de visualización y para hacer cálculos geométricos.

La transformación inversa, desde la representación poligonal hasta la repetición B, enfrenta, sin embargo, una serie de problemas relacionados con la complejidad en el reconocimiento de diferentes tipos de superficies, incluidas las de forma libre. Además, existe el problema del ruido en los modelos poligonales que aparecen típicamente como resultado del escaneo 3D.

El proceso general mediante el cual C3D B-Shaper transforma modelos de formatos poligonales a B-rep consta de tres etapas: segmentación, reconstrucción de superficies y construcción del modelo b-rep. El proceso de transformación es iterativo: si los usuarios no están contentos con los resultados, se pueden hacer correcciones durante las etapas de segmentación y reconstrucción de la superficie.


Transformando una representación poligonal en una B-rep

Sin embargo, antes de iniciar el proceso de transformación b-rep, mejoramos la calidad de la malla poligonal fuente mediante la aplicación de las siguientes soluciones: coordinar las direcciones de las normales en los polígonos adyacentes; eliminar agujeros; y aplique algoritmos de suavizado a fuentes de malla ruidosas, si las hay.

Segmentación del modelo poligonal.

La primera etapa de transformación es segmentar el modelo poligonal. Clasificamos el polígono de malla en subconjuntos (segmentos). La información sobre las normales en cada vértice de malla permite realizar una segmentación de primer orden y luego realizar la división de malla inicial, así como clasificar áreas como planas o altamente curvas. La división inicial de la malla se basa en la definición de bordes "afilados". Estos son los bordes entre dos polígonos triangulares donde el ángulo entre sus normales promedio excede un valor predefinido.

Una segmentación de segundo orden analiza la malla en función de su curvatura principal, que es suficiente para clasificar las superficies elementales. Al calcular las curvaturas en los vértices de malla, utilizamos los resultados del trabajo de Meyer (Mark Meyer, Mathieu Desbrun, Peter Schroder y Alan H. Barr, "Operadores discretos de geometría diferencial para múltiples colectores triangulados", Visualización y Matemáticas III, 2003) Al definir un operador diferencial discreto para regiones trianguladas: se considera un conjunto de vértices adyacentes (relacionados con un vértice dado a través de un borde) para cada vértice de malla inicial. A continuación, se calcula un operador discreto K para el vértice. Según el operador, las curvaturas promedio normal, media K _H y gaussiana K _G se definen en el vértice de la malla.


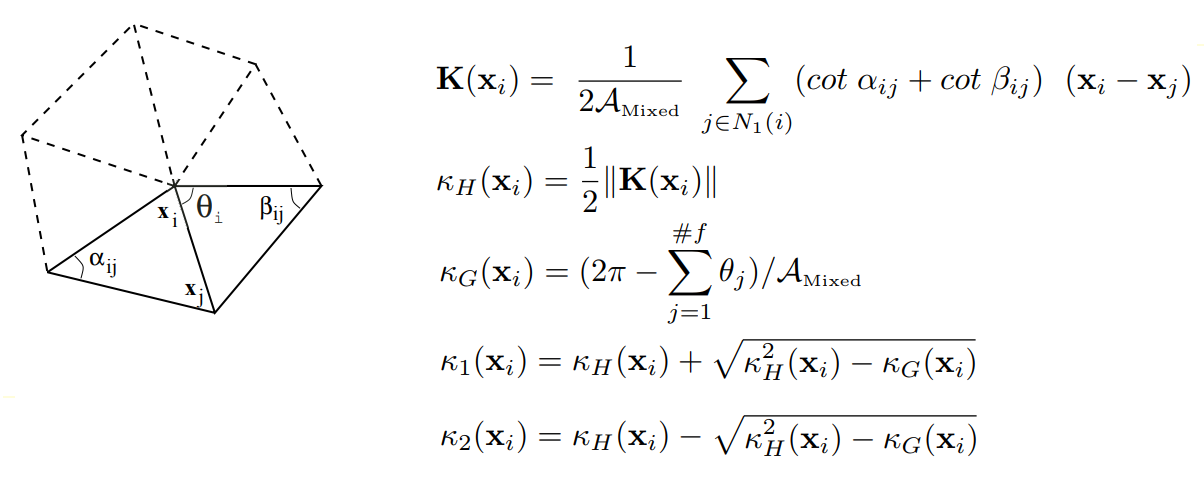Definición de operadores diferenciales discretos para regiones trianguladas

De esta manera, el tensor de curvatura se calcula para cada vértice de malla, del cual se extraen los valores de curvatura principal K ₁ y K ₂ y las direcciones de curvatura principal.

Los vértices de malla se clasifican por los valores de sus curvaturas principales K ₁ y K ₂ , y luego se calculan para ellos. El algoritmo de clasificación de vértices se basa en k-medias, es decir, minimiza la desviación cuadrática total de los puntos del grupo desde los centros de los grupos. El resultado resultante del algoritmo contiene un vértice de malla asociado con un clúster $$$Ci$y un par de curvaturas (cluster-center - L. Guillaume, "Segmentación de malla triangular basada en tensor de curvatura con rectificación de límites", Proceedings Computer Graphics International (CGI), 2004).


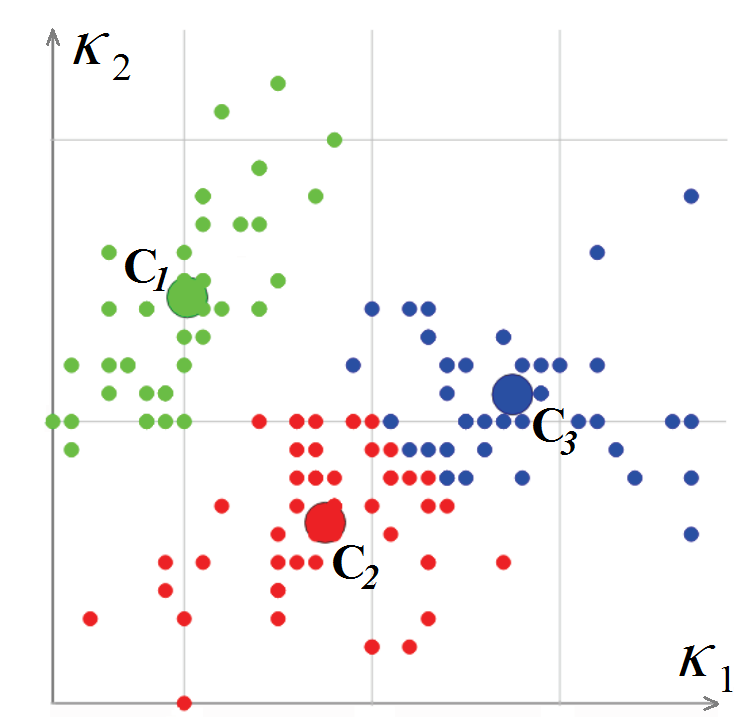Clasificación de vértices de malla poligonal en el espacio de curvatura

Una vez que terminamos de clasificar los vértices de la malla poligonal, pasamos a clasificar los polígonos. Para comenzar este procedimiento, elegimos un polígono triangular cuya curvatura puede considerarse completamente definida. Este es uno cuyos tres vértices están dentro de un solo grupo, o tiene dos vértices en un borde afilado. El polígono se etiqueta como un nuevo segmento y se convierte en el punto de partida para un procedimiento recursivo que expande el segmento: para cada polígono triangular, los polígonos adyacentes se consideran siempre que el borde entre ellos no esté "afilado". Cuando un vértice de polígono adyacente, que es opuesto a un borde común, está en un borde afilado o pertenece al mismo grupo, el polígono se agrega al segmento. El proceso se repite hasta que todos los polígonos que forman la malla desaparecieron.


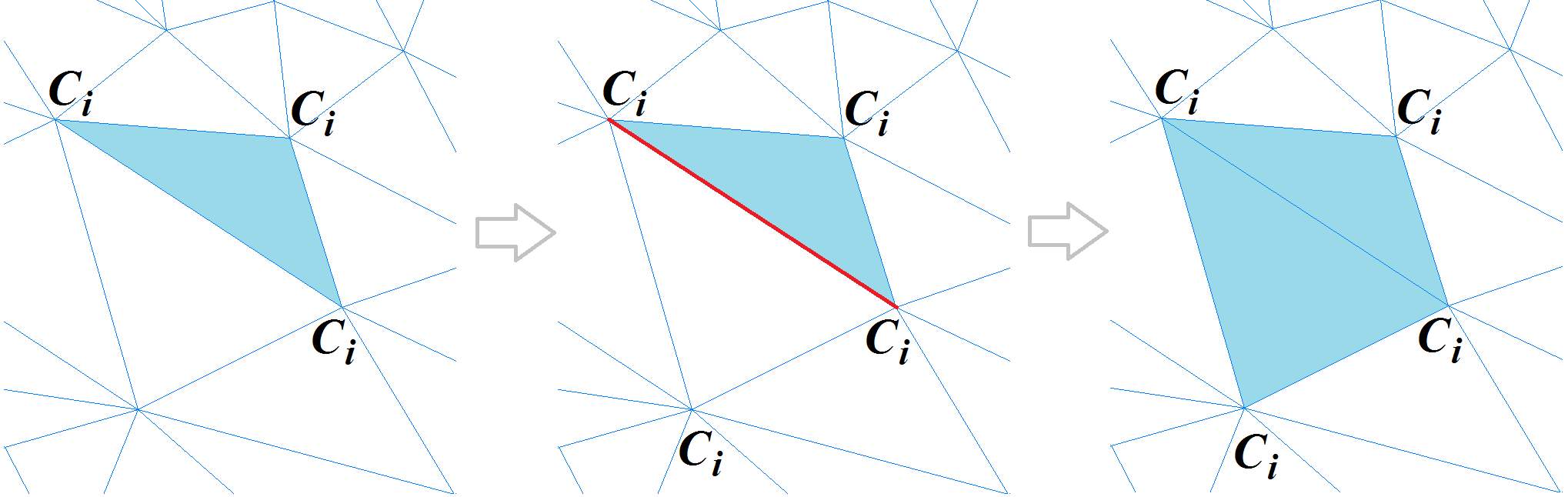Segmentación de malla poligonal

Una vez que se completa el procedimiento de creación de segmentos, otro algoritmo une los segmentos adyacentes para eliminar la segmentación excesiva de la malla.

Reconocimiento de tipo de superficie

La segunda etapa es el reconocimiento de superficie. Cada segmento debe aproximarse por una superficie con una precisión determinada por el sistema o por los usuarios.

En primer lugar, los valores de curvatura principal de los segmentos se utilizan para determinar si es posible describir la forma del segmento mediante una de las siguientes superficies elementales:

• Plano: k ₁ = k ₂ = 0
• Esfera: k ₁ = k ₂ = K > 0
• Cilindro: k ₁ = K > 0, k ₂ = 0
• Cono: k ₁ ∈ [ a , b ], k ₂ = 0
• Toroide: k ₁ = K , k ₂ ∈ [ a , b ]

Para crear superficies elementales, ajustamos objetos geométricos simples en conjuntos de puntos usando el algoritmo apropiado. Por ejemplo, para ajustar un círculo y una esfera en un conjunto de puntos, se utiliza el método de mínimos cuadrados; Para ajustar un plano, se utiliza el análisis de componentes principales. El sistema garantiza que cada superficie reconstruida esté relacionada con un segmento dentro de una precisión de reconocimiento predefinida.

La siguiente figura ilustra las superficies reconocidas por color: los planos se muestran en azul, los cilindros en rojo, las esferas en verde, los conos amarillos y los toroides violetas.


Malla poligonal de origen (izquierda) y malla segmentada (derecha) con segmentos de superficie reconocidos

Si ninguna superficie elemental puede describir el segmento, entonces el sistema intenta reconocer una superficie de extrusión o una superficie de revolución.

Cuando el sistema finalmente no puede encontrar una superficie analítica para describir la forma del segmento, se crea una superficie NURBS para ello.

Creación de modelo B-rep

La etapa final de la transformación es crear el modelo B-rep basado en la segmentación y los datos de superficie reconstruidos. Se crea un gráfico de adyacencia a partir de las regiones segmentadas para representar la topología del modelo y forma la base para crear el modelo B-rep resultante. Los modelos B-rep se ensamblan en un modo totalmente automático, en contraste con las etapas anteriores:

• Los bordes B-rep se crean a partir de curvas de intersección de superficies reconstruidas adyacentes
• Las caras B-rep están construidas por superficies reconocidas acotadas y bordes B-rep

Sin embargo, no siempre es posible crear un shell con la topología correcta. Por ejemplo, tome dos superficies como un cilindro y un plano que sean casi tangentes entre sí en el espacio. Debido a la tolerancia especificada para las superficies reconstruidas, es posible que no se crucen en absoluto. Como resultado, el shell creado puede tener defectos. Los usuarios pueden eliminar defectos corrigiendo los parámetros de la superficie.

Tipos de modelos poligonales

Existen numerosas fuentes de modelos poligonales disponibles en línea:

• Los catálogos y bases de datos en línea ofrecen modelos 3D en formatos poligonales como STL, VRML y OBJ de 3D Warehouse, Cults 3D, etc.
• Archivos que resultan del escaneo 3D
• Salida de la optimización topológica de modelos usando algoritmos CAE

Los modelos poligonales de estas fuentes se pueden dividir en dos grupos: modelos triangulados (mallados) a partir de objetos B-rep, y todos los demás modelos. Un par de características específicas del primer grupo es la ausencia de ruido de malla poligonal y el dominio de las superficies analíticas. Esto significa que los modelos del primer grupo se pueden transformar fácilmente en repeticiones b en modo totalmente automatizado o con un esfuerzo mínimo del usuario.

Las mallas poligonales de los modelos en el segundo grupo tienen ruido, contienen superficies orgánicas y, por lo tanto, es más probable que requieran la participación interactiva de los usuarios.

Por lo tanto, ofrecemos dos modos para operar C3D B-Shape, totalmente automático e interactivo. Los usuarios pueden cambiar entre los modos de reconocimiento y administrar los tipos de superficie durante el proceso de reconstrucción. La selección de un modo puede depender del propósito de realizar la transformación: los usuarios a veces pueden desear ignorar la conectividad topológica del shell resultante, o su corrección general. Este suele ser el caso cuando se optimiza la visualización en aplicaciones BIM, en las que los usuarios agregan elementos interiores personalizados al modelo arquitectónico.

Por otro lado, las tareas de ingeniería inversa requieren la copia más precisa posible de los modelos fuente para que el modelo resultante tenga una topología correcta. Por lo tanto, es necesario predefinir la precisión de, por ejemplo, la coaxialidad de los cilindros o la tangencia de dos superficies. En este tipo de casos, la participación de los usuarios en el proceso de transformación es crucial.

La transformación automática de C3D B-Shaper emplea las siguientes funciones que utilizan como datos de entrada la malla de origen y la configuración de transformación:

MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params ); 

Una de las configuraciones de transformación es un valor de precisión de reconocimiento que establece la tolerancia máxima para distancias entre vértices de segmento y superficies reconocidas. La precisión puede ser absoluta o relativa. Cuando se usa una precisión relativa, las desviaciones de las caras de los cuerpos de malla se miden en relación con el tamaño del modelo.

La clase de interfaz del procesador MbMesh ofrece opciones avanzadas para gestionar la segmentación y el reconocimiento de superficies:

 class MbMeshProcessor { .. public: // Mesh rectification. void SetUseMeshSmoothing( bool useSmoothing ); // Mesh segmentation management. const MbCollection & GetSegmentedMesh(); MbResultType SegmentMesh( bool createSurfaces = true ); void ResetSegmentation(); void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx ); MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep ); // Surface recognition management. void FitSurfaceToSegment( size_t idxSegment ); void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType ); const MbSurface * GetSegmentSurface( size_t idxSegment ) const; // B-rep shell construction. MbResultType CreateBRepShell( MbFaceShell *& pShell ); .. } 

Para, por ejemplo, corregir los resultados de la segmentación automática, C3D B-Shaper ofrece herramientas para fusionar y dividir segmentos, etc. Los usuarios pueden ajustar superficies de tipos dados en el segmento seleccionado, así como modificar los parámetros de superficies reconocidas.

Resumen

El resultado de los algoritmos de transformación de C3D B-Shaper se ilustra en las siguientes figuras, en las que un modelo 3D complejo se transforma con éxito de su representación de malla poligonal a un sólido de representación de límites.




Malla poligonal (izquierda) y modelo B-rep (derecha) convertidos con C3D B-Shaper

Nuestro objetivo es crear un SDK potente para transformar modelos de poligonal a B-rep, y así continúa el desarrollo de C3D B-Shaper. Algunas de las cosas en las que estamos trabajando incluyen el avance de los algoritmos de segmentación automática, el desarrollo de herramientas para la edición de segmentación, la mejora de la construcción de superficies NURBS de forma libre y la mejora de la calidad de los ensamblajes de shell B-rep.

Los clientes que usan el núcleo geométrico C3D también son un factor para impulsar el desarrollo de C3D B-Shaper.

Los desarrolladores pueden probar C3D B-Shaper como parte del C3D Toolkit o como un componente independiente.

Por Andrey Tumanin, líder de desarrollo de software en C3D Labs