Posit-aritmética: derrotando un punto flotante en su propio campo. Parte 1

Parte 2

Del traductor: El tema del formato Posit ya estaba en el centro aquí , pero sin detalles técnicos significativos. En esta publicación, traigo a su atención una traducción de un artículo de John Gustafson (autor de Posit) e Isaac Yonemoto en el formato Posit.
Como el artículo tiene un gran volumen, lo dividí en dos partes. La lista de enlaces está al final de la segunda parte.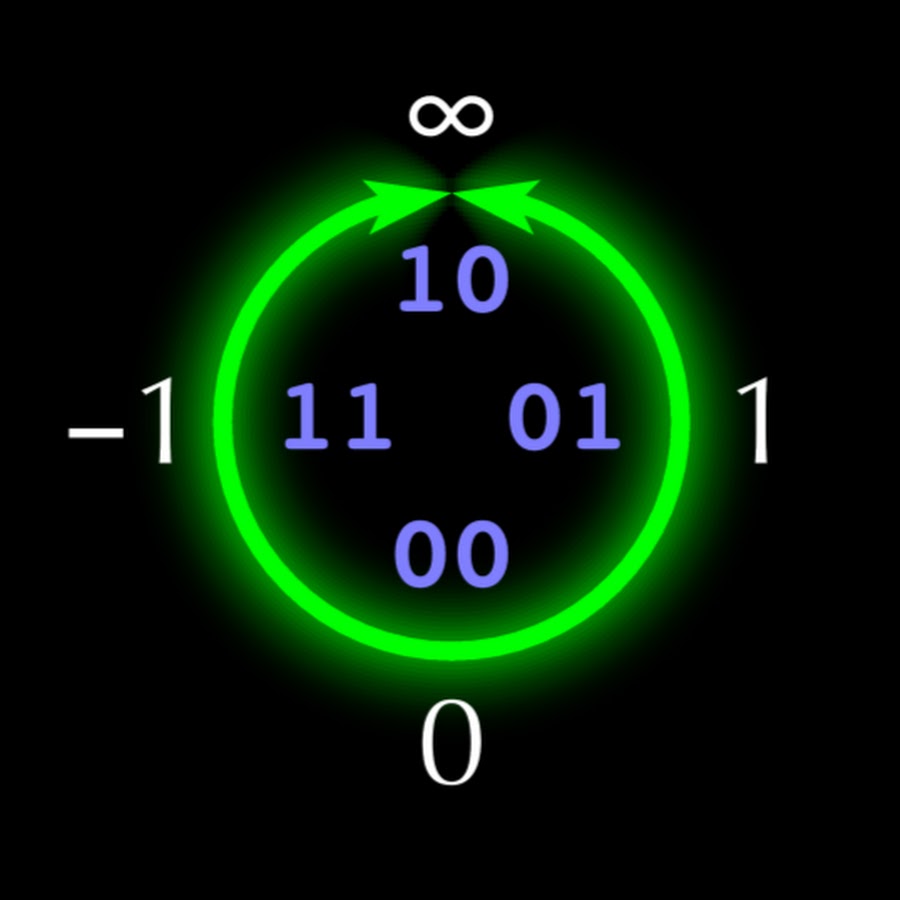



El nuevo tipo de datos, llamado posit, está diseñado como un reemplazo directo para los números de coma flotante del estándar IEEE 754. A diferencia de la forma anterior, aritmética unum, el estándar posit no requiere el uso de aritmética de intervalo o operandos de tamaño variable, y, como flotante, los números positivos se redondean si el resultado no se puede representar exactamente. Tienen ventajas innegables sobre el formato flotante, incluido un mayor rango dinámico, mayor precisión, coincidencia bit a bit de los resultados de los cálculos en diferentes sistemas, hardware más simple y soporte más simple para excepciones. Los números positivos no se desbordan ni al infinito ni a cero, y "no es un número" (No es un Número, NaN) son acciones, no combinaciones de bits. La unidad de procesamiento positivo es menos compleja que la FPU IEEE. Consume menos energía y ocupa un área de silicio más pequeña, por lo que el chip puede realizar significativamente más operaciones en números positivos por segundo que FLOPS, con los mismos recursos de hardware. Las GPU y los procesadores de aprendizaje profundo, en particular, pueden realizar más operaciones por vatio de consumo de energía, lo que mejorará la calidad de su trabajo.

Se llevaron a cabo pruebas exhaustivas comparando positividad y flotación en términos de precisión de cálculo para varias precisiones de positividad. Los números de posición con baja precisión son la mejor solución para "cálculos aproximados" en los casos en que la baja precisión es aceptable. Los números positivos de alta precisión proporcionan una mayor precisión que un flotante del mismo tamaño; en algunos casos, el positivo de 32 bits puede reemplazar con seguridad un flotante de 64 bits. En otras palabras, posit supera al flotante en su propio juego.

Teoría: Unums: Tipo I y Tipo II

El marco aritmético unum (números universales, número universal) tiene varias formas para representar números. La forma original es "Tipo I", un superconjunto de IEEE 754; ella usa ubit al final de la parte fraccionaria para indicar que el número real es exacto o está en el rango entre números reales adyacentes. A pesar de que Unum, como float, tiene un signo, exponente y parte fraccional, las longitudes del exponente y la parte fraccionaria varían automáticamente, de un bit a un cierto valor definido por el usuario. Unum Type I es una forma compacta de representar aritmética de intervalos, pero las longitudes variables requieren un esfuerzo adicional. Este tipo puede repetir el comportamiento de un flotante utilizando una función de redondeo especial.

La forma de número universal "Tipo II" [4] no es compatible con el flotador IEEE, y es un concepto limpio, matemáticamente riguroso basado en números reales proyectivos x. La idea clave aquí es que los enteros con signo en el código adicional se asignan elegantemente a números reales proyectivos, con la misma propiedad de cambiar de números positivos a negativos, y con el mismo orden en el eje numérico. Citando a William Kahan [5]:
“Ahorran espacio en la memoria porque no manipulan números, sino punteros a valores. Y esto hace posible hacer aritmética muy, muy rápido ".
La estructura del unum de 5 bits se muestra en la Fig. 1. Si cada unum tiene n bits, entonces la "retícula en U" llena el cuadrante superior derecho del círculo con un conjunto ordenado de $$$2 ^ {n-3} -1$ números reales $$$x_i$ (No necesariamente racional). En el cuadrante superior izquierdo son negativos $$$x_i$ reflejado en relación con el eje vertical. La mitad inferior del círculo contiene números que son inversos a los números de la mitad superior, reflejados desde el eje horizontal, lo que hace que las operaciones de multiplicación y división sean tan simétricas como la suma y la resta. Al igual que con el Tipo I, los números unum Tipo II terminan con 1 (ubit), que representa el intervalo abierto entre puntos exactos adyacentes para los cuales unum termina con 0 .


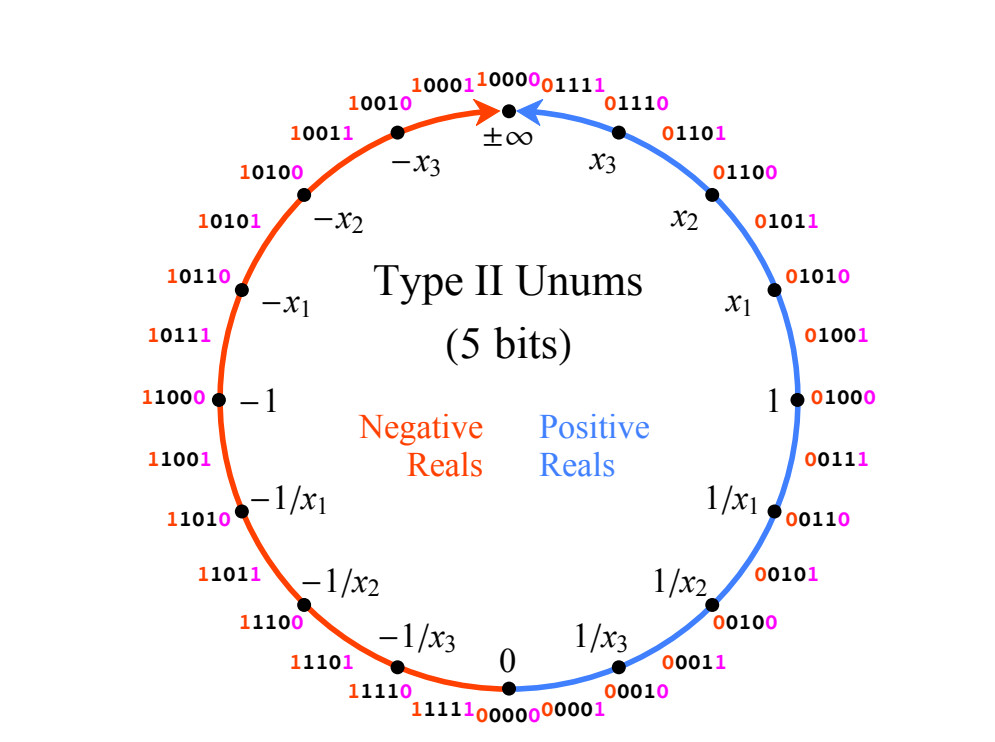Fig. 1. La línea de números reales proyectivos, mapeados a enteros en un código adicional de 4 bits de longitud.

Los números unum Tipo II tienen muchas propiedades matemáticas ideales, pero la mayoría de las operaciones con ellos se realizan mediante tablas de búsqueda . Si se necesitan n bits de precisión, entonces la tabla (en el peor de los casos) tendrá $$$2 ^ {2n}$ valores para la función de dos argumentos, pero teniendo en cuenta las simetrías y otros trucos, la tabla se puede reducir a un tamaño más aceptable. El tamaño de la tabla limita la escala de este formato ultrarrápido a 20 bits o menos para la tecnología actual. Los números unum tipo II tampoco se prestan bien para fusionar operaciones. Estas deficiencias sirvieron como motivación para encontrar un formato que conserve muchas de las propiedades de los números unum Tipo II, pero es más "amigable con el hardware" y puede calcularse mediante circuitos lógicos similares a las FPU existentes.

2. Los números Posit y Valid

Hay dos enfoques opuestos para los cálculos en números reales:

• No es estricto, pero es barato y aceptable para una gran cantidad de aplicaciones prácticas.
• Matemáticamente riguroso, incluso a costa del tiempo y la memoria.

La primera afirmación se refiere a la aritmética real, en la que el error de redondeo es lo suficientemente pequeño, la segunda afirmación se refiere a la aritmética de intervalos. Los números unum de los tipos I y II también pueden considerarse en una línea similar, y esta es una de las razones por las cuales son "números universales". Sin embargo, si siempre vamos a usar alguna función para redondear después de cada operación, entonces es mejor que no usemos el último bit como un bit significativo de la parte fraccional y no como ubit. El número unum de este tipo se llamará número positivo.

Cita del New Oxford American Dictionary, 3ra edición:

posit (sustantivo): Una declaración hecha en el supuesto de que resultará ser cierto.

Para simplificar la implementación del hardware, los números unum Tipo II debilitan una de las reglas: los valores inversos exactos solo existen para 0, $$$\ pm \ infty$ y grados dos. Esto nos permite llenar la cuadrícula en U para que los números finales sigan siendo similares al flotante y tengan el formulario $$$m \ cdot2 ^ k$ donde k y m son enteros. No hay intervalos abiertos.

Válido es un par de números positivos de igual tamaño, cada uno de los cuales termina en ubit. Están destinados a usarse en aquellas aplicaciones en las que es importante determinar estrictamente en qué intervalo se encuentra el número, por ejemplo, al depurar algoritmos numéricos. Los valores válidos son más potentes que la aritmética de intervalos ordinarios y menos propensos a expandir rápidamente los límites de intervalos excesivamente pesimistas [2, 4]. Sin embargo, no son el tema de esta publicación.

La figura 2 muestra la estructura de la representación positiva de n bits con bits exponentes.


Figura 2. Formato positivo generalizado para los valores finales distintos de cero

El bit de signo contiene 0 para números positivos, 1 para negativos. Para números negativos, encuentre el Suplemento 2 antes de decodificar el modo, el exponente y la parte fraccional. Para comprender los bits de modo, considere las cadenas binarias que se muestran en la Tabla 1, en la que k significa la longitud de la secuencia principal yx en el flujo de bits significa un estado indiferente.

Tabla 1. Significado de longitud de ejecución k de los bits de régimen



Llamamos a la longitud de la secuencia inicial el modo de número. Las cadenas binarias comienzan con un cierto número de ceros o unos en una fila, seguidos del bit opuesto, o se alcanza el final de la cadena. Los bits de modo se resaltan en ámbar, el bit opuesto se resalta en marrón. Sea m el número de bits idénticos en la secuencia, si estos bits son cero, entonces k = -m, si 1, entonces k = m-1. La mayoría de los procesadores pueden encontrar la primera unidad en una palabra o el primer cero en una palabra en hardware, es decir, la lógica de decodificación ya está disponible. Modo significa un factor de escala igual a $$$usado ^ k$ donde $$$utilizado = 2 ^ {2 ^ {es}}$ . La Tabla 2 muestra un ejemplo de valores utilizados.

Tabla 2. utilizada como función es



Los siguientes bits (resaltados en azul en la figura) son el exponente e, que se refiere a un entero sin signo. No se desplaza, como se hace en carrozas, representa escalar a $$$2 ^ e$ . Puede haber hasta bits de exponente, dependiendo de cuántos bits quedan a la derecha de los bits de modo. Esta es una forma compacta de cambiar la precisión; los números cercanos a 1 en valor absoluto tienen mayor precisión que los números muy grandes o muy pequeños, que son mucho menos comunes en los cálculos.

Si quedan bits después del modo y los bits de exponente, representan la parte fraccionaria, f, al igual que la parte fraccionaria 1.f en formato flotante, pero el bit oculto es siempre 1. No hay números desnormalizados con 0 oculto, a diferencia del flotante.

El sistema que describimos es una consecuencia natural de llenar la cuadrícula en U. Comencemos con un simple post de 3 bits, para mayor claridad, en la fig. La Figura 3 muestra solo la mitad derecha de los números reales proyectivos. Entonces, los números en la fig. 3. Obedecer las reglas de tipo II. Solo hay dos valores especiales: 0 (todos los bits son 0) y ± ∞ (una unidad seguida de todos los ceros), su secuencia de bits no sigue la notación posicional. Para otros valores positivos en la Figura 3., los bits se colorean como se describió anteriormente. Tenga en cuenta que todos los valores positivos en la Figura 3 son valores exactos utilizados en grados k representados por bits de modo.


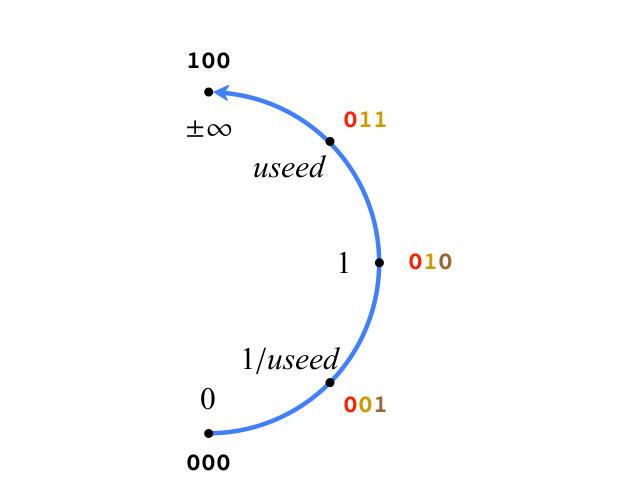Fig.3. Valores positivos de posit de 3 bits

La precisión de los números Posit aumenta a medida que se agregan los bits, y los valores permanecen donde están en el círculo cuando se agrega el bit 0. Cuando se agrega 1, se crea un nuevo valor entre los dos valores positivos en el círculo. ¿Qué valor numérico debemos asignarles? Deje que maxpos sea el valor positivo más grande y minpos el valor positivo más pequeño en el círculo definido por la cadena de bits. En la Figura 3, se usa maxpos y minpos es 1 / usado. Las reglas de interpolación son las siguientes:

Entre maxpos y ± ∞, el nuevo valor es maxpos × utilizado; entre 0 y minpos, el nuevo valor es minpos / utilizado (con un nuevo bit de modo)
Entre valores existentes $$$x = 2 ^ m$ y $$$y = 2 ^ n$ , donde myn difieren en más de 1, el nuevo valor será su media geométrica, $$$\ sqrt {x \ cdot y} = 2 ^ {(m + n) / 2}$ (con un nuevo bit exponente).
En otros casos, el nuevo valor se encuentra en el medio entre las xey existentes, es decir, es una media aritmética, $$$(x + y) / 2$ (con un nuevo bit fraccional)

Como ejemplo, la fig. 4 muestra la construcción de números positivos de 2 a 5 bits con es = 2 y, por lo tanto, se usa = 16.


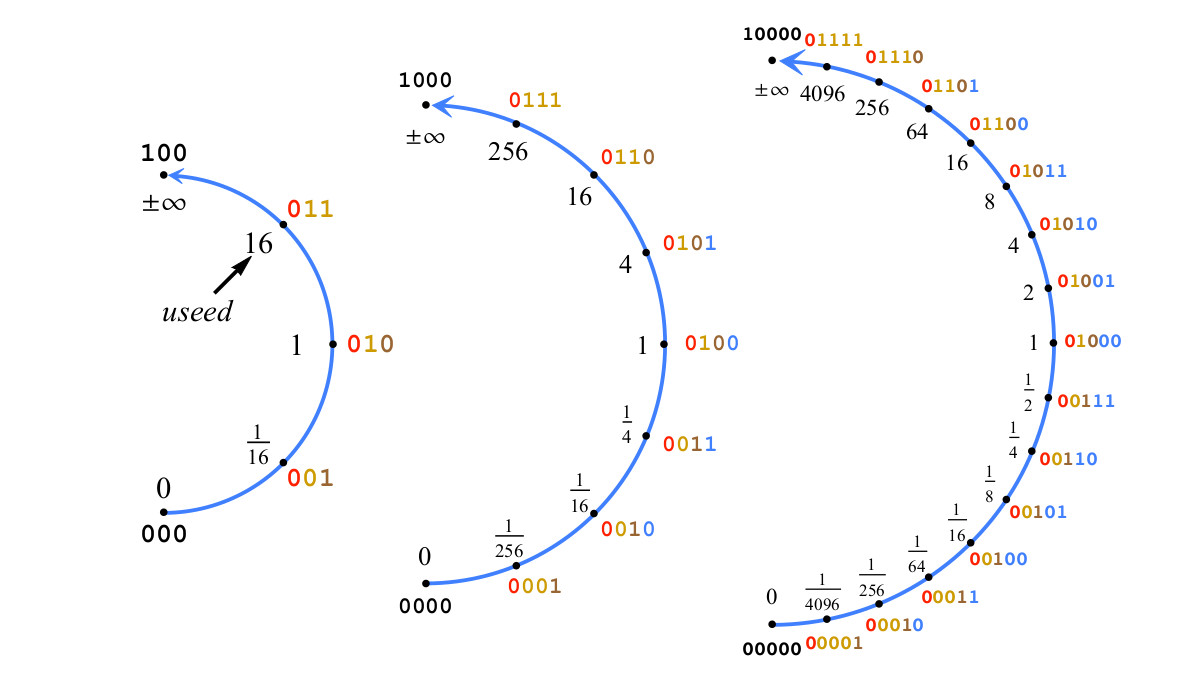Fig. 4. Construyendo un Posit con dos bits de un exponente, $$$es = 2, usado = 2 ^ {2 ^ {es}} = $ 1$

Si en la fig. 4 agregue un bit más para obtener un positivo de 6 bits, a los números positivos que representan los rangos de valores entre 1/16 y 16, se agregará el bit de la parte fraccional, no el bit exponente. Considere una cadena de bits que representa el número posit p como un entero con signo, que va desde $$$-2 ^ {n-1}$ antes $$$2 ^ {n-1} -1$ . Sea k un número entero que representa bits de modo, e un número sin signo que representa bits exponentes, si está presente. Si el conjunto de bits es una parte fraccional $$$\ {f_1f_2 ... f_ {f_s} \}$ posiblemente vacío, entonces sea f un valor que representa un número $$$1, f_1f_2 ... f_ {f_s}$ . Entonces p representa

$$

$$x = \ begin {cases} 0, & p = 0, \\ \ pm \ infty, & p = -2 ^ {n-1}, \\ sign (p) \ times used ^ k \ times 2 ^ e \ times f \, & \ text {any other} p \ end {cases}$$

Los bits de modo y es realizan la misma función que los bits exponenciales en el flotador estándar, juntos determinan un factor de escala igual a una potencia de dos, y cada incremento utilizado significa un cambio $$$2 ^ {es}$ poco El número de maxpos es $$$usado ^ {n-2}$ y minpos es igual $$$usado ^ {2-n}$ . Un ejemplo de decodificación del número positivo se muestra en la Fig. 5 (con un valor "no estándar" para es, por simplicidad).


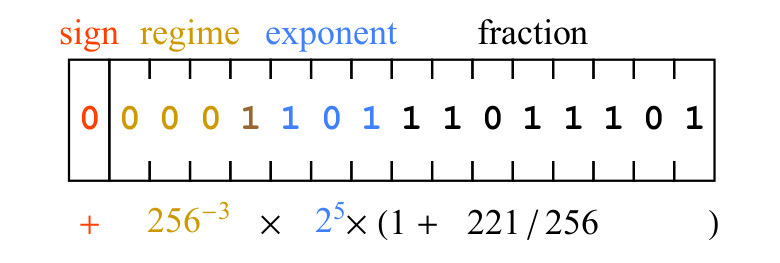Fig. 5. Un ejemplo de la cadena de bits posit y su significado matemático

Un bit de signo 0 significa que el valor es positivo. Los bits del modo 0001 tienen una secuencia de tres ceros, lo que significa que k = -3, por lo tanto, el factor de escala introducido por los bits del modo es $$$256 ^ {- 3}$ . Los bits de exponente, 101, representan 5 como un entero binario sin signo, y el factor de escala de inserción es $$$2 ^ 5$ . Finalmente, los bits de la parte fraccionaria 11011101 representan el número 221, es decir, la parte fraccionaria es 1 + 221/256. La expresión escrita debajo del campo de bits en la Figura 5. nos lleva al resultado $$$477/134217728 \ aprox3.55393 \ times10 ^ {- 6}$

2.2. Entrenamiento de 8 bits positivo y red neuronal

A pesar de que el estándar IEEE no define flotantes de 8 bits, los números positivos de 8 bits con es = 0 han demostrado su utilidad para algunos propósitos, son muy útiles para construir redes neuronales [3, 8]. Actualmente, los números IEEE de media precisión (16 bits) a menudo se usan para estos fines, pero los números positivos de 8 bits pueden procesarse potencialmente de 2 a 4 veces más rápido. Una función importante en las redes neuronales es el sigmoide, que tiene una asíntota de 0 para $$$x \ to- \ infty$ y 1 para $$$x \ to \ infty$ . Vista general de la función sigmoidea $$$1 / (1 + e ^ {- x})$ , y es costoso para los cálculos, y puede requerir fácilmente más de cien ciclos del procesador para llamar a la función exp (x) desde la biblioteca, y debido a la división. Con los números positivos, simplemente puede invertir el primer bit del número positivo que representa x, desplazar el número 2 bits a la derecha, llenar los bits de la izquierda con ceros y la función positiva resultante, que se muestra en la Figura 6. morado, cerca del sigmoide (se muestra en verde), e incluso tiene la misma pendiente al cruzar el eje y.


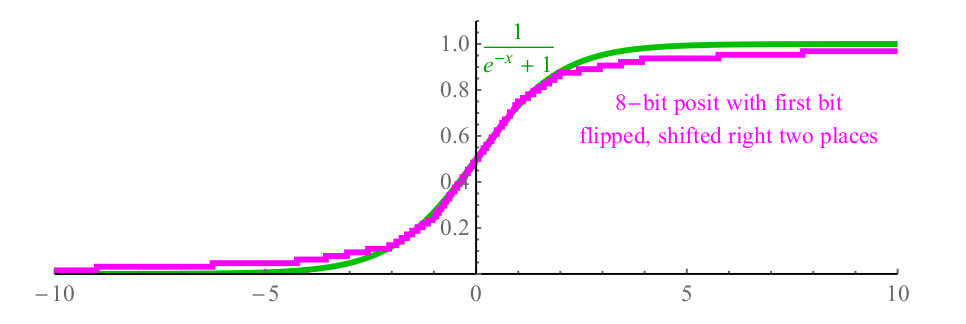Fig. 6. Función sigmoidea rápida utilizando representación positiva

2.3. Utilizado para lograr y superar el rango dinámico de flotación

Definimos el rango dinámico del sistema numérico como el número de órdenes decimales desde el valor final positivo más pequeño hasta el más grande, desde minpos hasta maxpos. Es decir, el rango dinámico se define como $$$log_ {10} (maxpos) −log_ {10} (minpos) = log_ {10} (maxpos / minpos)$ . Para un posit de 8 bits con es = 0, minpos es 1/64 y maxpos es 64, por lo que el rango dinámico es 3.6 órdenes decimales. Los números positivos definidos con es = 0 son elegantes y simples, pero sus versiones de 16 y 32 bits tienen un rango dinámico más pequeño que un flotante IEEE del mismo tamaño. Por ejemplo, un flotador IEEE de 32 bits tiene un rango dinámico de 83 décadas, pero un positivo de 32 bits con es = 0 tendrá un rango dinámico de solo 18 décadas.

A continuación se muestra una tabla de valores es que permiten que los números positivos superen el rango dinámico de flotante para tamaños de 16 y 32 bits, y se acercan a él para tamaños de 64, 128 y 256 bits.

Tabla 3. Rangos dinámicos de flotante y positivo para un número igual de bits



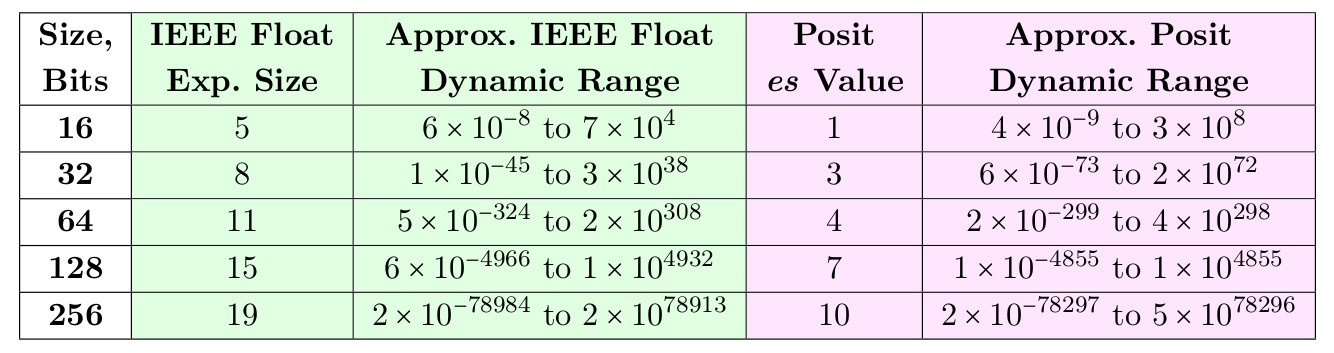
Una de las razones para elegir es = 3 para el positivo de 32 bits es que en este caso pueden servir como un reemplazo simple no solo para un flotante de 32 bits, sino también para 64 bits. Del mismo modo, el rango dinámico de 17 décadas para posit de 16 bits les allana el camino en aplicaciones que actualmente utilizan flotantes de 32 bits. Mostramos que posit puede superar al flotante tanto en rango dinámico como en precisión con el mismo tamaño de bit.

2.4. Comparación cualitativa de formatos flotante y positivo

No hay "NaN" en el formato positivo, en cambio, los cálculos se interrumpen, y el controlador de interrupciones debe informar un error o de alguna manera procesar el error y continuar el cálculo, pero los números positivos no permiten la asignación de un cierto valor que indica un error lógico , que, por definición, es el número. Esto simplifica enormemente el hardware. Si el programador ve la necesidad de usar valores NaN, esto muestra que el programa aún no se ha completado, y se deben usar números válidos en el entorno de depuración para encontrar y eliminar tales errores. Además, posit no tiene $$$+ \ infty$ y $$$- \ infty$ , como flotante, sin embargo, los números válidos admiten intervalos abiertos $$$(maxpos, + \ infty)$ y $$$(- \ infty, -maxpos)$ , que hacen posible representar un valor ilimitado de cualquier signo, y la necesidad de infinito con signo solo significará que en lugar de números positivos, debe aplicar valores válidos.

También en la vista positiva no hay "cero negativo", cero negativo, este es otro defecto lógico que existe en el estándar flotante IEEE. Con números positivos, si a = b, entonces f (a) = f (b). El estándar IEEE 754 dice que el número inverso a -0 es $$$- \ infty$ , y el número inverso a +0 es $$$+ \ infty$ , pero también dice que -0 es +0. Por lo tanto, se entiende que $$$- \ infty = + \ infty$ ?

Los números flotantes tienen un sofisticado algoritmo de comparación a = b. Si cualquiera de (a, b) es NaN, el resultado de la comparación siempre es negativo, incluso si su representación de bits es la misma. Si la representación de bits es diferente, entonces todavía existe la posibilidad de que a sea igual a b, ¡ya que un cero negativo es igual a un cero positivo! En posix, la verificación de igualdad es la misma que para los enteros: si los bits son iguales, los números son iguales. Si algún bit es diferente, no son iguales. Los números positivos tienen la misma relación (a <b) que los enteros con signo que con los enteros con signo, debe asegurarse de que no haya desbordamiento con un cambio en el signo, pero no necesita instrucciones de máquina separadas para comparar el positivo, si tiene instrucciones para comparar enteros con signo.

En el formato positivo, no hay números desnormalizados, es decir, no hay una combinación especial de bits que muestre que el bit oculto es 0 en lugar de 1 . Posit no usa anti-overflow, en cambio, se usa una disminución gradual de la precisión, que proporciona la funcionalidad de anti-overflow y su caso simétrico, overflow (a diferencia de posit, el flotante estándar es asimétrico y usa estos patrones de bits para representar un conjunto grande e inútil de valores de NaN).

El formato flotante tiene una ventaja sobre posit, cuando se desarrolla hardware, una disposición fija de los bits del exponente y la parte fraccionaria les permite decodificarse en paralelo.En formato positivo, debe seguir alguna secuencia, primero decodificando los bits de modo y luego los bits restantes. Hay una manera simple de sortear esta restricción, similar a un truco utilizado para aumentar la velocidad de manejo de excepciones en flotante: se agregan varios bits adicionales a cada valor para que almacenen información de tamaño al decodificar la instrucción.

3. Compatibilidad bit a bit y operaciones combinadas

Una de las razones por las que IEEE float no da resultados idénticos en diferentes sistemas es porque para funciones elementales, como $$$log(x)$ y $$c o s ( x ) según el estándar IEEE no requiere precisión hasta el último bit para ninguna entrada posible. El entorno positivo debe redondear correctamente todos los resultados de las operaciones aritméticas compatibles. (Algunos programadores de la biblioteca matemática están preocupados por el "dilema del dilema de la tabla", que es que para algunos valores puede ser muy costoso determinar su redondeo correcto, esto puede eliminarse usando tablas de interpolación en lugar de aproximaciones polinómicas). Valor incorrecto en el último bit de la función$cos(x)$$$e x , por ejemplo, puede conducir finalmente a un sistema informático que nos dice que 2 + 2 = 5.La razón más fundamental por la que el flotador IEEE no produce resultados duplicados en diferentes sistemas es que el estándar permite el uso de métodos velados para evitar el desbordamiento / anti-desbordamiento y para mejorar la precisión de las operaciones, como almacenar internamente un bit de acarreo adicional para exponencial y fraccional partes La aritmética positiva prohíbe tales trucos ocultos.$e^x$



La última versión (2008) del estándar IEEE 754 [7] incluye una operación combinada de multiplicación-suma en los requisitos. Este fue un cambio controvertido, no aprobado por muchos miembros del comité. Las operaciones combinadas retrasan la operación de redondeo hasta que la última operación en el cálculo, que incluye más de una operación, se complete después de que se completen todas las operaciones, incluidas las operaciones de enteros exactos. La combinación de operaciones no es lo mismo que las operaciones aritméticas de precisión expandibles, que pueden aumentar la longitud de los enteros hasta que la memoria de la computadora se llene.

El entorno positivo requiere la presencia de las siguientes operaciones combinadas:

Multiplicación-suma combinada$$( a × b ) + c Suma-multiplicación combinada$(a\times b)+c$
$$( a + b ) × c Multiplicación-Multiplicación-Resta combinada$(a+b)\times c$
$$( a × b ) - ( c × d ) Suma combinada$(a\times b)-(c\times d)$
$$∑ a i Multiplicación escalar combinada$\sum a_i$
$$∑ a i b i Tenga en cuenta que todas las operaciones de la lista anterior son un subconjunto de la multiplicación escalar combinada [6] en términos de requisitos de hardware del procesador. El número más pequeño que no es cero que se puede obtener usando la multiplicación escalar es$\sum a_i b_i$

$$$minpos^2$ . Cualquier producto es un número entero $$$minpos^2$ . Si queremos obtener un producto escalar de vectores $$$\{maxpos, minpos\}$ y $${ m a x p o s , m i n p o s } como una operación exacta en la zona de rascado, necesitamos un conjunto lo suficientemente grande como para almacenar$\{maxpos, minpos\}$$$$maxpos^2/minpos^2$ . Recordemos que $$$maxpos=useed^{n-2}$ y $$$minpos=1/maxpos$ . De esta manera $$$maxpos^2/minpos^2=useed^{4n-8}$ .Teniendo en cuenta los bits de transferencia y redondeando a la potencia de dos, obtenemos los valores recomendados que se dan en la Tabla 4.

Tabla 4. Tamaños exactos de la batería para cada tamaño positivo:



en algunos casos, el tamaño de la batería es comparable al tamaño del registro, en otros casos, se requiere una zona de cero equivalente a la caché L1 o L2. Las operaciones combinadas pueden realizarse mediante software o hardware, pero deben estar disponibles para su ejecución en un entorno positivo.