Cómo el enredo cuántico ayudará en la detección de ondas gravitacionales

Recientemente hicimos un experimento para probar un nuevo enfoque para reducir el ruido cuántico en LIGO y escribimos un artículo al respecto, ver arXiv: "Demostración de la mejora del interferómetro a través del enredo EPR" . Y aquí les diré qué tipo de ruido cuántico en LIGO, cómo se pueden reducir y qué tienen que ver con el entrelazamiento cuántico y la luz exprimida.

Artículo de UPD publicado en Nature Photonics .

1. Sensibilidad LIGO y ruido cuántico

Hablé sobre cómo funciona el detector y qué ruido hay en él en detalle en la última publicación sobre el Telescopio Einstein . El detector tiene una amplia variedad de ruidos: sísmicos, térmicos, cuánticos y otros, y todos interfieren con el registro de una señal de ondas gravitacionales.


Las principales contribuciones a la sensibilidad de LIGO a diferentes frecuencias, normalizadas a la amplitud de la GW (cepa).

Toda la dificultad para crear un detector de ondas gravitacionales es reducir estos ruidos. La mayoría de estos ruidos no son fundamentales, sino más bien limitaciones técnicas. Y solo los ruidos cuánticos surgen de la naturaleza misma del aparato de medición. Se convertirán en el principal obstáculo para una mejor sensibilidad en los detectores futuros, por lo que nos detendremos en ellos con más detalle. Hay dos ruidos cuánticos: ruido de disparo y ruido de presión de radiación.

El ruido de disparo surge debido a la naturaleza cuántica del láser: el rayo láser consiste en fotones que vuelan con diferentes retrasos aleatorios entre sí. Cuando estos fotones se miden en fotodiodos, las fluctuaciones en el flujo de fotones conducen a fluctuaciones de corriente y, como resultado, a ruido en la señal que observamos.

El ruido de la presión de radiación es el segundo lado de la naturaleza cuántica de la luz. Como se sabe por el electromagnetismo clásico desde la época de los experimentos de Lebedev, un objeto sobre el que brilla la luz experimenta la presión de la luz . Es fácil de entender si consideramos un fotón como una partícula: cada partícula lleva un impulso, que se transmite al cuerpo al impactar. Es decir, cuando el láser brilla en un espejo móvil, el espejo comienza a moverse bajo la influencia de la presión de la luz. Y dado que los fotones se distribuyen aleatoriamente, a veces llegan más fotones al espejo durante un intervalo de tiempo determinado, a veces menos, y esta fuerza de presión ligera también es aleatoria. Entonces: la cuantización de la luz conduce a una fuerza aleatoria que actúa sobre los espejos en LIGO. Esta fuerza provoca un desplazamiento aleatorio de los espejos, que se registra a la salida del interferómetro como una señal espuria.


Explicación sobre el ruido cuántico. Una distribución aleatoria del número de fotones produce una fuerza aleatoria de presión de radiación (izquierda). Por otro lado, una distribución aleatoria de fotones en el tiempo conduce a fluctuaciones de amplitud en el fotodetector (derecha). Ambos ruidos dependen de la longitud de onda, la potencia de la luz y la longitud del hombro. El ruido de la presión de radiación es menor, mayor es la masa de los espejos. Crédito: [1].

El ruido de la presión de radiación es más fuerte cuanto mayor es el poder de la luz incidente en los espejos (es decir, el flujo de fotones). La señal del GW también aumenta al aumentar la potencia de la luz en el detector. El ruido de disparo normalizado a la señal disminuye. Como resultado, resulta que puede aumentar la sensibilidad limitada por el ruido de disparo al aumentar la potencia de la luz, pero tendrá que pagar con el aumento del ruido de la presión de radiación. Y viceversa. No hay forma en la forma clásica de suprimir tanto el ruido cuántico a la vez. Tendrá que usar tecnología cuántica.


Dependencia de la sensibilidad a la potencia de la luz: el ruido de disparo (azul) disminuye y el ruido de presión de radiación (verde) aumenta proporcionalmente.

2. Luz comprimida

Hay un maravilloso artículo sobre Habré sobre luz exprimida por qbertych . Si no sabe qué es la luz comprimida, le recomiendo que primero lea su artículo. Seré breve

Si observa la luz como una onda, los parámetros característicos no serán el flujo de fotones y el retraso entre ellos, sino la amplitud y la fase de la onda. Usualmente hablan de cuadraturas de luz de fase y amplitud.

$$$$ display $$ E = E_0 \ cos (\ omega_0 t + \ phi) = E_0 \ cos \ omega_0 t \ cos \ phi - E_0 \ sin \ omega_0 t \ sin \ phi = \\ = E_ {} \ sin \ omega_0 t + E_ {a} \ cos \ omega_0 t $$ display $$

Si la señal de interés para nosotros está contenida en la fase de luz, y es lo suficientemente pequeña, entonces podemos hacer una aproximación:

$$$$ display $$ E_ {f} = E_0 \ sin \ phi \ aprox E_0 \ phi; \ quad E_ {a} = E_0 \ cos \ phi \ approx E_0 $$ display $$

Por lo tanto, el valor$$ $ en línea $ E_ {f} $ en línea $ llamada fase en cuadratura: contiene información sobre la fase.

En consecuencia, el ruido de disparo es una fluctuación de la fase de la luz, y el ruido de la presión de radiación es causado por fluctuaciones de amplitud.

La incertidumbre en la fase y la incertidumbre en la amplitud están relacionadas por la relación de Heisenberg:

$$$$ display $$ \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ {a} \ leq \ frac {1} {2} $$ display $$

En un rayo láser convencional, estas incertidumbres son iguales. Sin embargo, es posible comprimir la incertidumbre en la fase aumentando la incertidumbre de amplitud; lo principal es que su producto satisface la relación de incertidumbre. Tal luz se llama exprimida:

$$$$ display $$ \ Delta ^ 2 E_ {f} ^ {sqz} = e ^ {- 2r} \ Delta ^ 2 E_ {f}, \ Delta ^ 2 E_ {a} ^ {sqz} = e ^ {2r } \ Delta ^ 2 E_ {a} \\ \ Delta ^ 2 E_ {f} ^ {sqz} \ Delta ^ 2 E_ {a} ^ {sqz} = \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ { a} \ leq \ frac {1} {2}, $$ display $$

donde r es la relación de compresión.

En términos generales, incluso en ausencia de un haz potente, siempre existen fluctuaciones de vacío . También se pueden comprimir para obtener un vacío comprimido: en promedio, el número de fotones en él es cero, pero las fluctuaciones de la amplitud y la fase se comprimen.


Son las fluctuaciones de vacío que ingresan al detector a través del puerto de señal que son la fuente del ruido cuántico en LIGO. Por lo tanto, si este vacío se comprime en fase, esto reducirá el ruido de disparo en el detector.

Este enfoque se ha utilizado en el detector GEO600 durante los últimos 8 años, reduciendo el ruido de disparo cuatro veces, y desde este año también se ha implementado en LIGO, reduciendo el ruido de disparo a la mitad (lo que aumenta el número de eventos registrados en 8 veces).



Izquierda: un ejemplo de sensibilidad LIGO mejorada con luz exprimida. Derecha: la mejor compresión hasta la fecha se creó en nuestro grupo hace varios años: las fluctuaciones de vacío se suprimieron en 15 dB.

Sin embargo, no todo es tan simple: según la relación de incertidumbre, si comprimimos la fase, aumentamos las fluctuaciones de amplitud. Y aumentan el ruido de la presión de radiación. Y nuevamente, debe elegir qué ruido reducir al aumentar el otro. Pero, ¿es posible evitar esta limitación de alguna manera?

3. Compresión dependiente de la frecuencia

Afortunadamente, dos ruidos cuánticos limitan la sensibilidad del detector a diferentes frecuencias: con bajo nivel de ruido, la presión de radiación es mucho más fuerte que la presión de disparo, y a niveles altos, y viceversa. Por lo tanto, es posible preparar una compresión de luz complicada, donde a bajas frecuencias la luz se comprime en amplitud (y, por lo tanto, el ruido de la presión de radiación disminuye), y a altas frecuencias, en fase (y, por lo tanto, se reduce el ruido de disparo).


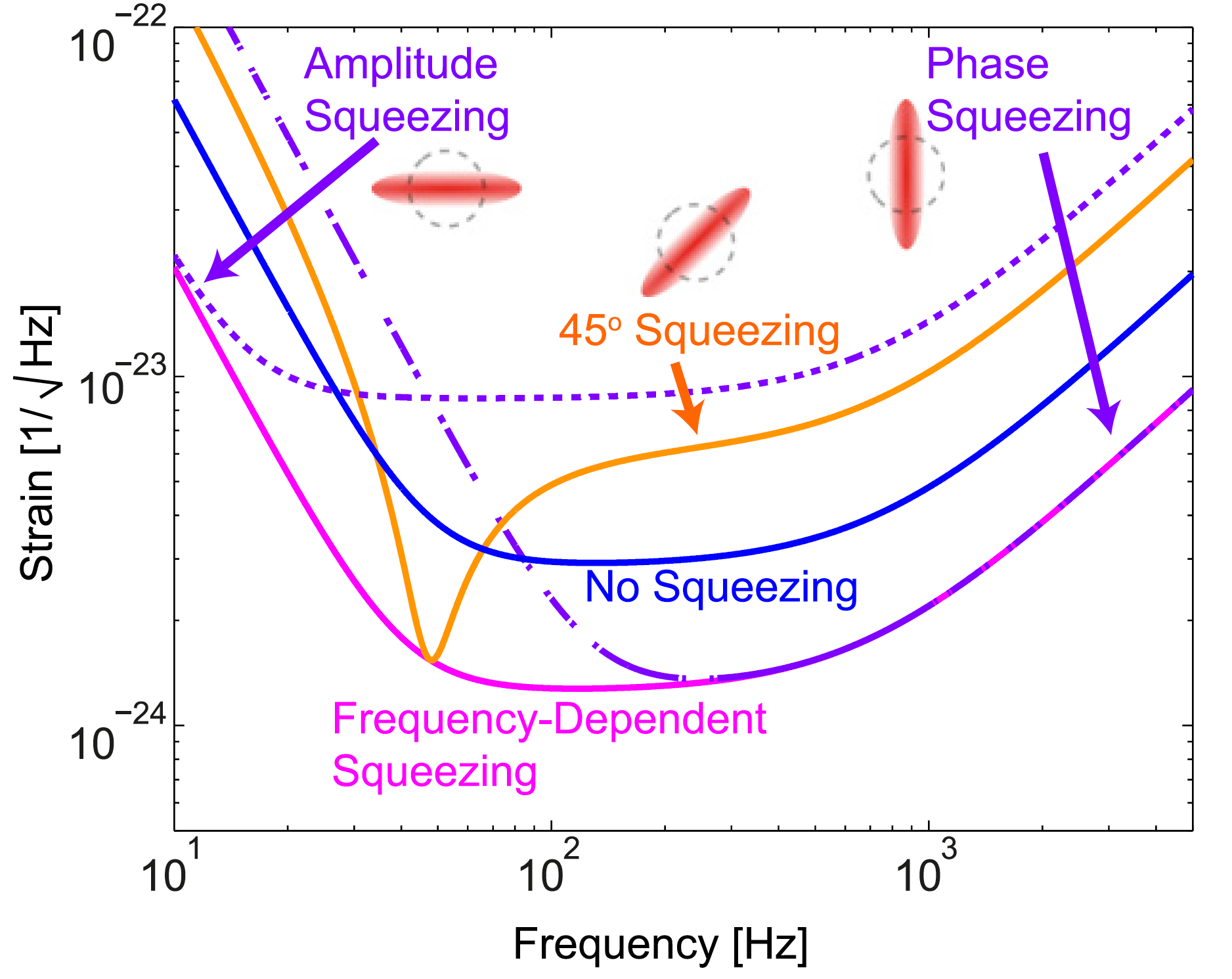Compresión dependiente de la frecuencia: a diferentes frecuencias, se comprime la amplitud, la fase o una combinación de las mismas. Como resultado, la sensibilidad mejora en todas las frecuencias. [SSY Chua et al 2014 Clase. Quantum Grav. 31 183001]

Fundamentalmente, la razón de la necesidad de una compresión dependiente de la frecuencia es que la presión de radiación en los espejos también crea una compresión ligera, pero en una cuadratura diferente. Esto se puede ver en la imagen a continuación: si usa compresión convencional en la entrada, adquiere una dependencia de frecuencia en la salida debido a la presión de radiación. Para "cancelar" esta dependencia de frecuencia, debe establecer la dependencia inversa para la compresión en la entrada.


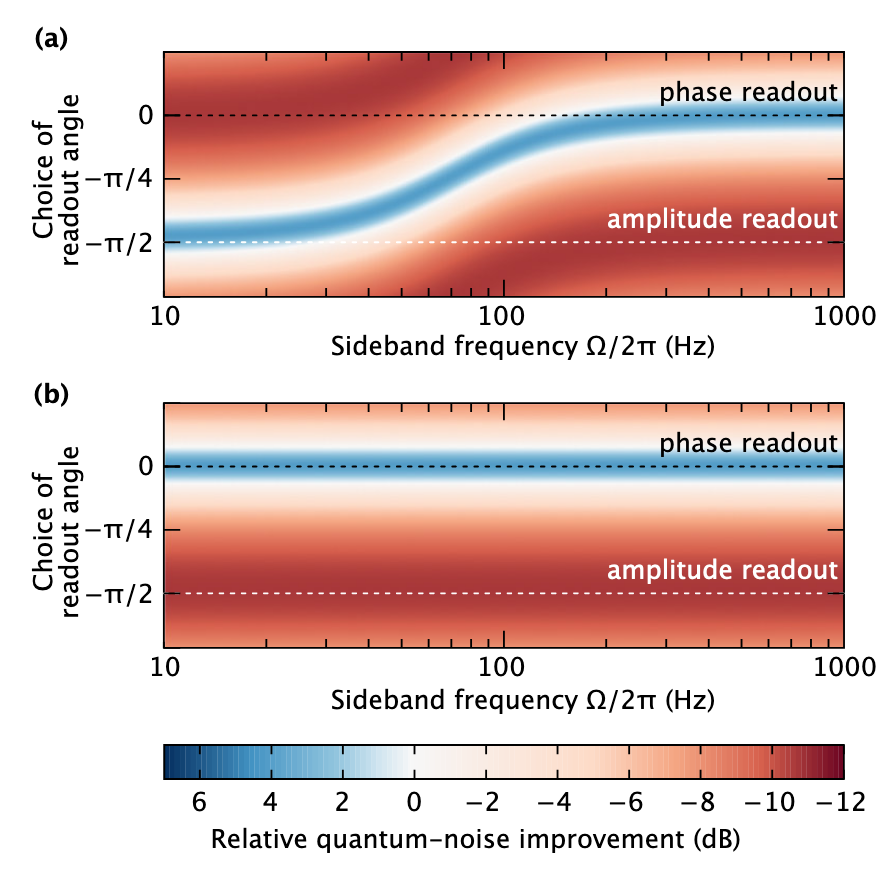Un ejemplo del artículo: la dependencia de mejorar la sensibilidad del interferómetro cuando se usa la compresión convencional en función de la frecuencia y las diferentes fases de medición se muestra arriba: la señal está en cuadratura de fase, y se puede ver que si la sensibilidad aumenta a frecuencias altas (color azul), entonces a frecuencias bajas disminuye (rojo ) El uso de la compresión dependiente de la frecuencia puede mejorar la sensibilidad en todas las frecuencias.

Entonces, conceptualmente resolvemos el problema de reducir el ruido cuántico en todas las frecuencias, la pregunta sigue siendo: cómo implementar tal dependencia de frecuencia. Para hacer esto, necesita descubrir cómo convertir la fase comprimida en una amplitud comprimida. De hecho, es muy simple: producir un cambio de fase:

$$$$ display $$ E_ {f} ^ {sqz} = E_0 e ^ {- 2r} \ sin (\ phi) \ rightarrow E_0 e ^ {- 2r} \ sin (\ phi + \ pi / 2) = E_ { a} e ^ {- 2r} $$ mostrar $$

Por lo general, un simple espejo es suficiente para cambiar la fase, lo que cambiará la longitud del camino que recorre la luz. Sin embargo, en este caso, necesita un dispositivo que cree un cambio de fase dependiente de la frecuencia: no cambie la fase a frecuencias altas, sino a bajas$$ $ en línea $ \ pi / 2 $ en línea $ .

Actualmente, el concepto principal de crear compresión dependiente de la frecuencia en todos los diseños de detectores futuros es el uso de resonadores de filtrado adicionales. Si el vacío comprimido se refleja desde dicho resonador cuando se desintoniza desde la frecuencia de resonancia, adquirirá la dependencia de frecuencia necesaria. Sin embargo, tiene una gran dificultad: para crear la dependencia de frecuencia requerida, los resonadores deben tener varios cientos de metros de largo en el vacío, y esto es muy costoso y difícil de controlar. Tenemos otra idea

El hecho es que en el detector en sí ya hay muchos resonadores de tamaños adecuados, bajas pérdidas y un método de control bien conocido, pero no se pueden usar directamente; para la compresión dependiente de la frecuencia, es necesario desintonizar la resonancia. Pero cada resonador tiene muchas frecuencias resonantes, mientras que el detector solo funciona en una de ellas. La idea es utilizar una resonancia diferente , reflejando la luz exprimida del interferómetro para obtener la dependencia de frecuencia necesaria. La pregunta sigue siendo: cómo usar la dependencia de frecuencia creada a una frecuencia diferente de la frecuencia de trabajo principal del láser. Y luego el enredo cuántico viene al rescate.

4. Enredo cuántico y la paradoja EPR

La cuestión de la naturaleza del enredo es, sin duda, digna de un artículo separado. Discutí un poco más de complejidad en un artículo anterior sobre el Habré, así que aquí solo describiré brevemente sus principales propiedades. Comencemos con la paradoja EPR (Einstein-Podolsky-Rosen): tres caballeros notaron que hay una trampa en la mecánica cuántica. Por un lado, existe el principio de incertidumbre, que dice que es imposible medir con precisión la coordenada y el momento de una partícula al mismo tiempo (y en nuestro caso, la amplitud y la fase de la luz). Por otro lado, uno puede hacer un experimento tan simple: tomar el evento de descomposición de partículas, en el que nacen dos partículas idénticas. De acuerdo con la ley de conservación del momento, se dispersarán en direcciones opuestas a la misma velocidad. Si medimos el momento de una partícula, sabremos exactamente el momento de la segunda. Si medimos la coordenada de la segunda partícula, sabremos simultáneamente tanto la coordenada (la medimos) como el momento (lo predijimos a partir de la medición de la primera partícula), lo que, al parecer, es imposible debido a la relación de incertidumbre. La paradoja visible se resuelve introduciendo el concepto de enredo de partículas: dos partículas no son independientes entre sí, se describen mediante una función de onda. Esta función de onda no es local: hasta el momento de la medición es imposible decir cuál de las partículas voló en qué dirección. En cierto sentido, ambos volaron en ambas direcciones a la vez, y solo en el momento de la medición hubo una elección aleatoria de qué partícula se midió. Sus coordenadas e impulso están conectados de modo que la relación de incertidumbre no se aplica a su valor relativo. Además, si se actúa sobre una de las partículas, por ejemplo, por alguna fuerza, la segunda partícula también "siente" esta fuerza: sus parámetros medidos cambiarán en consecuencia.

Entonces, para nosotros lo más importante: si tenemos dos partículas, podemos predecir con precisión las propiedades de la segunda partícula midiendo la primera. Podemos poner una fuente de influencia en el camino de una partícula, y actuará en dos a la vez. Una vez realizada la medición correcta, podemos ver el resultado de este efecto.

Cómo lo usamos (se propuso por primera vez en un artículo en Nature Physics [2]). El papel de las partículas en el EPR lo desempeñan dos haces de vacío comprimido a dos frecuencias: la frecuencia fundamental del interferómetro y la frecuencia de la próxima resonancia del resonador. Los confundimos, uno de ellos (alta frecuencia) se refleja desde el resonador sintonizado y se mide. Obtiene una dependencia de frecuencia. Como los rayos están enredados, esta dependencia de la frecuencia también se transmite al haz a la frecuencia fundamental. Después de la medición, podemos predecir las señales en el haz principal idealmente con una precisión perfecta. Para hacer esto, medimos por separado en dos detectores separados y procesamos los datos de manera óptima.


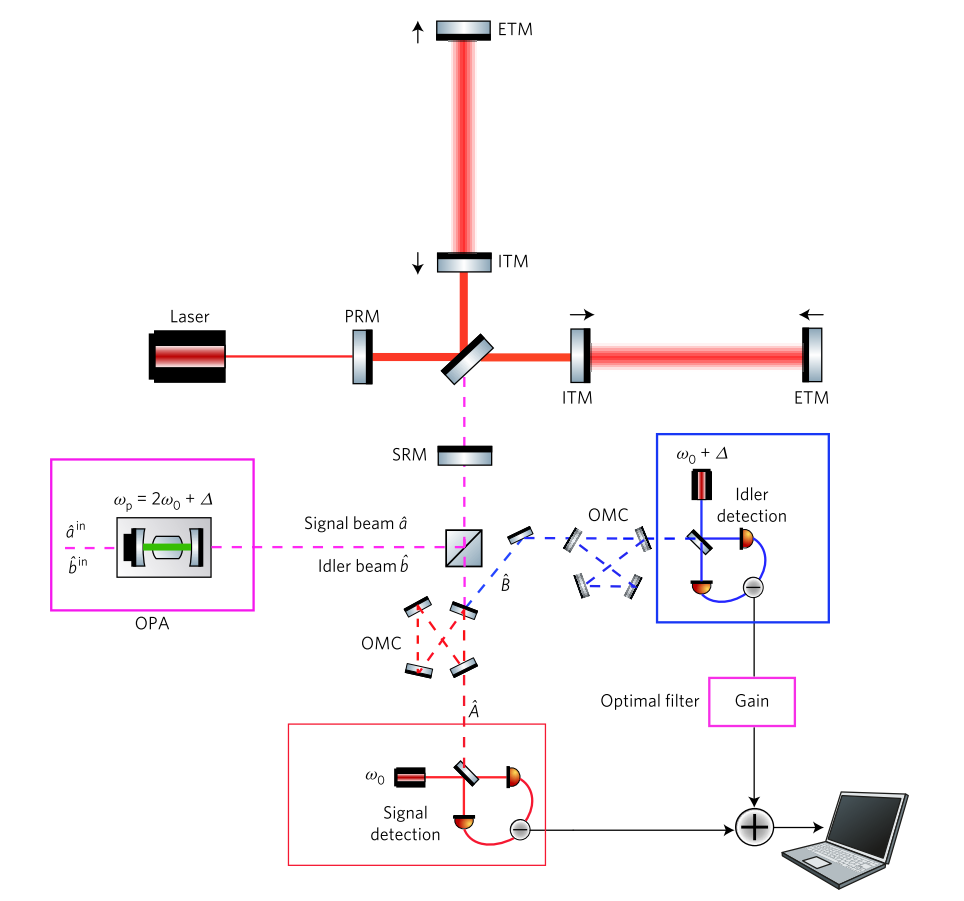Un esquema completo de compresión dependiente de la frecuencia basado en el enredo de [2]. OPA (amplificador óptico paramétrico) crea dos haces entrelazados de vacío comprimido a diferentes frecuencias, los cuales se envían al detector. Un haz a una frecuencia portadora resuena en el interferómetro. Se desintoniza un haz a una frecuencia alta de una de las resonancias más altas. En la salida, los rayos se separan y se detectan en dos detectores de homodina diferentes, después de lo cual se procesan de manera óptima.

5. Experimento

Nuestro experimento no incluye un interferómetro completo con espejos móviles. En cambio, estamos explorando la posibilidad de obtener una compresión dependiente de la frecuencia utilizando luz entrelazada reflejada por un resonador.


Diseño experimental simplificado. En lugar de un interferómetro completo, tenemos un resonador óptico de 2.5 m de largo. En lugar de dos detectores de homodina diferentes, usamos un detector, pero dos haces de referencia de diferentes frecuencias.

Como escribí anteriormente, en un interferómetro, la presión de radiación crea una dependencia de la frecuencia de la luz comprimida, lo que estropea la sensibilidad del detector. Para cancelar esta dependencia de frecuencia, necesitamos crear una dependencia de frecuencia inversa de la luz comprimida. En nuestro experimento, la sensibilidad no estropea la presión de radiación (no tenemos espejos móviles), sino la desintonización del detector por resonancia (vea la imagen a continuación (a)). Cuando se mide en una cuadratura de señal (lectura de fase), esto estropea la sensibilidad a bajas frecuencias (rojo).

Para restaurar la sensibilidad, reconstruimos un rayo adicional (inactivo) a partir de resonancia en la dirección opuesta. Luego, después de la medición, podemos restaurar completamente la sensibilidad. En términos de EPR, podemos predecir el resultado de medir la cuadratura de fase con mayor precisión utilizando luz cuántica entrelazada.


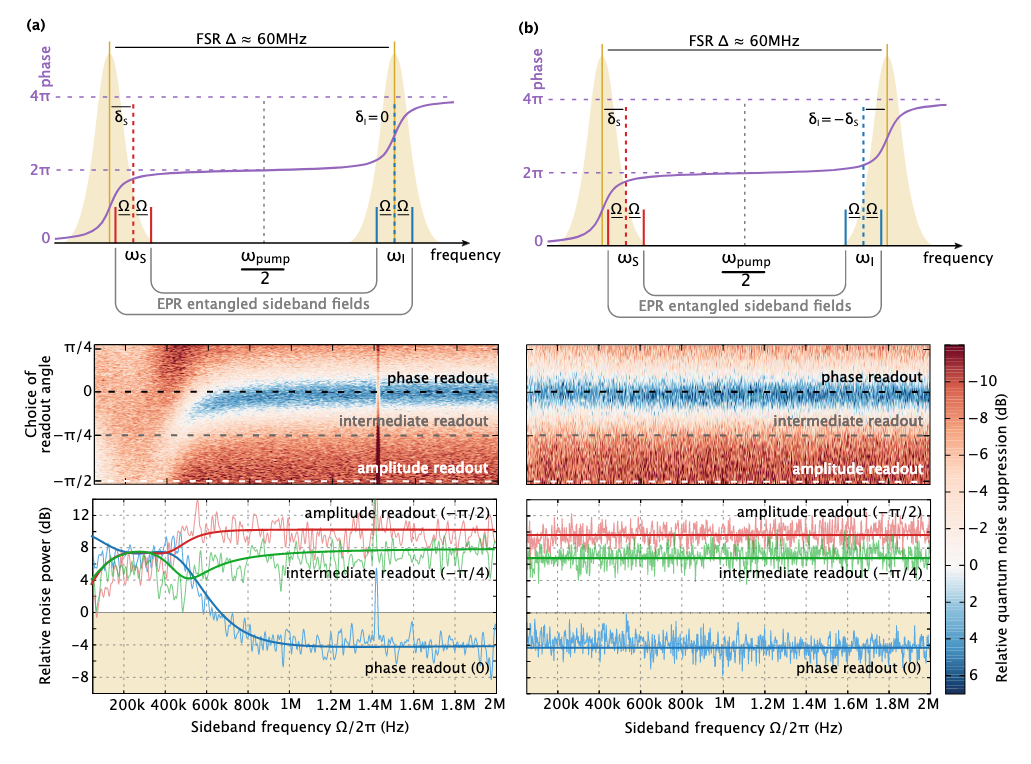Dos experimentos para observar la compresión dependiente de la frecuencia. En la primera (a), ajustamos el haz de señal a partir de la resonancia del detector, estropeando así la sensibilidad en la cuadratura de fase (y creando una dependencia de la frecuencia de la luz comprimida). En el segundo, creamos una dependencia de frecuencia adicional del segundo rayo (ocioso) y debido al entrelazamiento cuántico entre los dos rayos, la señal y el ilder pudieron restaurar la sensibilidad dañada al cancelar la dependencia de frecuencia introducida en el primer experimento.

En la imagen de arriba, la dependencia de frecuencia en (a) es bastante borrosa. Esto se debe a limitaciones en el procesamiento posterior: idealmente, se necesitan dos detectores de homodina separados, cuyas señales se pueden filtrar de manera óptima. Sin embargo, en otro modo, podemos obtener una hermosa dependencia de la frecuencia de la luz comprimida si reconstruimos ambos rayos a partir de resonancia en una dirección. Tal esquema no es relevante para el detector, pero da una idea de las opciones de instalación. Bueno, solo hermosos datos experimentales :)

6. Conclusión

Para resumir. Las fluctuaciones cuánticas de la luz son la fuente principal y más fundamental de ruido en todos los detectores modernos y futuros. Para suprimirlos, uno puede usar correlaciones cuánticas: luz exprimida. Sin embargo, para reducir el ruido en todo el rango de frecuencias del detector, es necesario comprimir las fluctuaciones de amplitud a bajas frecuencias y las fluctuaciones de fase a altas frecuencias. Se propone que dicha compresión dependiente de la frecuencia se lleve a cabo utilizando resonadores de filtrado especiales. Tradicionalmente, tales resonadores son muy caros y difíciles de implementar. Nuestra alternativa es usar el detector en sí mismo como un resonador de filtro, usando luz cuántica enredada. Hicimos un experimento y demostramos que el enredo cuántico en realidad permite realizar esta idea.

Este enfoque no es una panacea, por desgracia: hay que pagar por conveniencia. Para que el concepto funcione completamente, es necesario usar dos detectores de homodina, lo cual es bastante difícil experimentalmente. Además, el segundo detector agrega ruido a la sensibilidad, aunque mucho menos de lo que puede obtener de la compresión.

En este trabajo, jugamos con complejidades y luz exprimida y mostramos cómo podemos usarlos para mejorar la sensibilidad de los detectores futuros.Pero, por supuesto, este es solo el primer paso en un largo camino para implementar este enfoque en un detector real: debe verificar cómo funciona todo con un interferómetro real, con espejos móviles, dos homodinas, etc. En general, el trabajo aún está lleno.

Para aquellos interesados ​​en los detalles, vea nuestro artículo y el artículo donde se presentó por primera vez la idea [2].

[1] Detectores GW de S. Hild Beyond 2nd Generation
[2] Y. Ma et al, Propuesta para la detección de ondas gravitacionales más allá del límite cuántico estándar a través del entrelazamiento EPR, volumen 13 de Nature Physics, páginas 776–780 (2017)

7. Varios

Y ahora algunas noticias sobre LIGO:

1. LIGO 26 3. https://gracedb.ligo.org/superevents/public/O3/ , .
2. , , . , , N+1 Scientific American . , .
3. 100 . , (c 55 130 ). , , .
4. LIGO , , , . . LIGO . , , . , , , , .

: , , : @hbar_universe .