Regresión lineal y métodos para su restauración.

Fuente: xkcd

La regresión lineal es uno de los algoritmos básicos para muchas áreas relacionadas con el análisis de datos. La razón de esto es obvia. Este es un algoritmo muy simple y comprensible, que ha contribuido a su uso generalizado durante muchas decenas, si no cientos, de años. La idea es que asumimos una dependencia lineal de una variable en un conjunto de otras variables, y luego tratamos de restaurar esta dependencia.

Pero este artículo no se trata de aplicar regresión lineal para resolver problemas prácticos. Aquí discutiremos características interesantes de la implementación de algoritmos distribuidos para su recuperación que encontramos al escribir un módulo de aprendizaje automático en Apache Ignite . Un poco de matemática básica, los conceptos básicos del aprendizaje automático y la informática distribuida lo ayudarán a descubrir cómo restaurar la regresión lineal, incluso si los datos se distribuyen en miles de nodos.

De que estas hablando

Nos enfrentamos a la tarea de restaurar la dependencia lineal. Como entrada, se dan muchos vectores de variables supuestamente independientes, cada una de las cuales está asociada con un cierto valor de la variable dependiente. Estos datos se pueden representar en forma de dos matrices:

$$

$$\ begin {pmatrix} a_ {11} y a_ {12} y a_ {13} & ... & a_ {1n} \\ a_ {21} y a_ {22} y a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} y a_ {m2} y a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

Ahora, dado que se asume la dependencia, y además es lineal, escribimos nuestra suposición en forma de un producto de matrices (para simplificar la notación aquí y abajo, se supone que el término libre de la ecuación $$$x_n$ y la última columna de la matriz $$$A$ contiene unidades):

$$

$$\ begin {pmatrix} a_ {11} y a_ {12} y a_ {13} & ... & a_ {1n} \\ a_ {21} y a_ {22} y a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

Muy similar a un sistema de ecuaciones lineales, ¿verdad? Parece, pero lo más probable es que no haya soluciones para tal sistema de ecuaciones. La razón de esto es el ruido que está presente en casi todos los datos reales. Además, la razón puede ser la falta de una relación lineal como tal, que puede intentar combatir introduciendo variables adicionales que dependen no linealmente de la fuente. Considere el siguiente ejemplo:

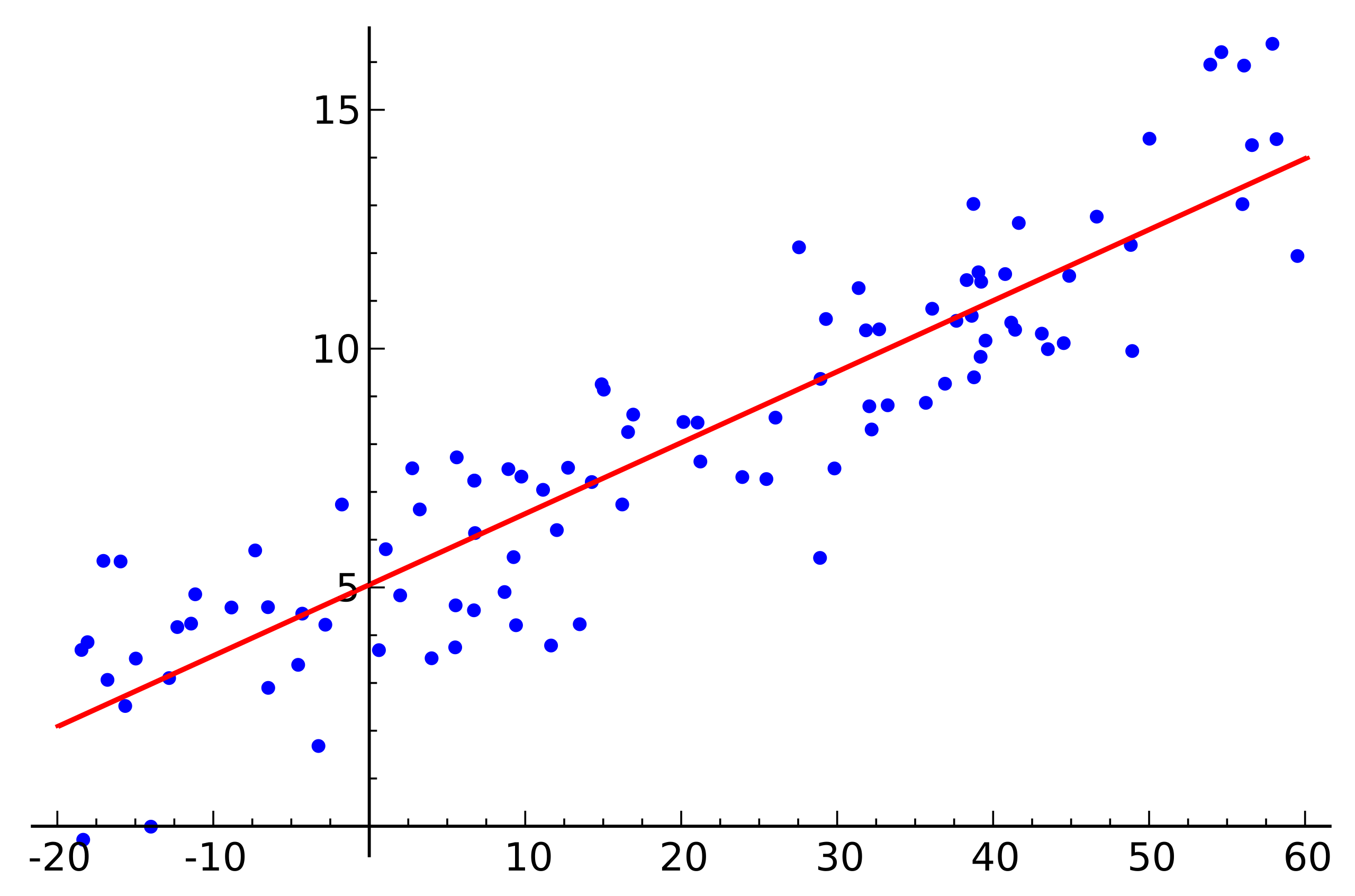Fuente: Wikipedia

Este es un ejemplo de regresión lineal simple que muestra la dependencia de una variable (a lo largo del eje $$$y$ ) de otra variable (a lo largo del eje $$$x$ ) Para que el sistema de ecuaciones lineales correspondientes a este ejemplo tenga una solución, todos los puntos deben estar exactamente en una línea recta. Pero esto no es así. Pero no se encuentran en una línea recta precisamente por el ruido (o porque la suposición de la presencia de una dependencia lineal era errónea). Por lo tanto, para restaurar una dependencia lineal de los datos reales, generalmente es necesario introducir una suposición más: los datos de entrada contienen ruido y este ruido tiene una distribución normal . Se pueden hacer suposiciones sobre otros tipos de distribución de ruido, pero en la gran mayoría de los casos, la distribución normal se discutirá más adelante.

Método de máxima verosimilitud

Entonces, asumimos la presencia de ruido aleatorio normalmente distribuido. ¿Cómo estar en tal situación? Para este caso, en matemáticas existe y se usa ampliamente el método de máxima verosimilitud . En resumen, su esencia radica en la elección de la función de probabilidad y su posterior maximización.

Volvemos a la restauración de la dependencia lineal de los datos con ruido normal. Tenga en cuenta que la relación lineal asumida es una expectativa matemática $$$\ mu$ Distribución normal disponible. Al mismo tiempo, la probabilidad de que $$$\ mu$ asume uno u otro valor, siempre que haya observables $$$x$ , se ve de la siguiente manera:

$$

$$P (\ mu \ mid X, \ sigma ^ 2) = \ prod_ {x \ in X} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}}$$

Sustituimos ahora en su lugar $$$\ mu$ y $$$X$ variables que necesitamos:

$$

$$P (x \ mid A, B, \ sigma ^ 2) = \ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}}}, a_i \ en A, b_i \ en B$$

Solo queda encontrar el vector $$$x$ a la cual esta probabilidad es máxima. Para maximizar dicha función, es conveniente prologarizar primero (el logaritmo de la función alcanzará su máximo en el mismo punto que la función misma):

$$

$$f (x) = ln (\ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix ) ^ 2} {2 \ sigma ^ 2}}}) = \ sum_ {i \ in [1, m]} ln \ frac {1} {\ sigma \ sqrt {2 \ pi}} \; - \ sum_ {i \ in [1, m]} \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}$$

Lo que, a su vez, se reduce a minimizar la siguiente función:

$$

$$f (x) = \ sum_ {i \ in [1, m]} (b_i-a_ix) ^ 2$$

Por cierto, esto se llama el método de mínimos cuadrados . A menudo, se omite todo el razonamiento anterior y este método simplemente se usa.

Descomposición QR

El mínimo de la función anterior se puede encontrar si encuentra el punto en el que el gradiente de esta función es cero. Y el gradiente se escribirá de la siguiente manera:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1, m]} 2a_i (a_ix - b_i) = 0$$

La descomposición QR es un método matricial para resolver el problema de minimización utilizado en el método de mínimos cuadrados. En este sentido, reescribimos la ecuación en forma de matriz:

$$

$$A ^ T A x = A ^ Tb$$

Entonces, presentamos la matriz $$$A$ en matrices $$$Q$ y $$$R$ y realice una serie de transformaciones (el algoritmo de descomposición QR en sí no se considerará aquí, solo su uso en relación con la tarea):

$$

$$\ begin {align} & (QR) ^ T (QR) x = (QR) ^ Tb; \\ & R ^ T Q ^ T Q R x = R ^ T Q ^ T b; \\ \ end {align}$$

Matriz $$$Q$ es ortogonal Esto nos permite deshacernos del trabajo. $$$Q Q ^ T$ :

$$

$$\ begin {align} & R ^ T R x = R ^ T Q ^ T b; \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b; \\ & R x = Q ^ T b. \ end {align}$$

Y si reemplazas $$$Q ^ T b$ en $$$z$ resultará $$$R x = z$ . Dado que $$$R$ es la matriz triangular superior, se ve así:

$$

$$\ begin {pmatrix} r_ {11} & r_ {12} & r_ {13} & r_ {14} & ... & r_ {1n} \\ 0 & r_ {22} & r_ {23} & r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & r_ {44} & .. . & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ begin {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}$$

Esto se puede resolver mediante el método de sustitución. Artículo $$$x_n$ es como $$$z_n / r_ {nn}$ artículo anterior $$$x_ {n-1}$ es como $$$(z_ {n-1} - r_ {n-1, n} x_n) / r_ {n-1, n-1}$ Y así sucesivamente.

Vale la pena señalar aquí que la complejidad del algoritmo resultante mediante el uso de descomposición QR es $$$O (2 millones ^ 2)$ . Además, a pesar de que la operación de multiplicación de matrices está bien paralela, no es posible escribir una versión distribuida efectiva de este algoritmo.

Descenso de gradiente

Hablando de minimizar una determinada función, siempre vale la pena recordar el método de descenso de gradiente (estocástico). Este es un método de minimización simple y efectivo basado en el cálculo iterativo del gradiente de una función en un punto y luego desplazándolo hacia el lado opuesto al gradiente. Cada uno de estos pasos lleva la solución al mínimo. El gradiente se ve igual:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1, m]} 2a_i (a_ix - b_i)$$

Este método también está bien paralelo y distribuido debido a las propiedades lineales del operador de gradiente. Tenga en cuenta que en la fórmula anterior, los términos independientes están bajo el signo de la suma. En otras palabras, podemos calcular el gradiente independientemente para todos los índices $$$i$ desde el primero hasta $$$k$ , en paralelo con esto, calcule el gradiente de los índices con $$$k + 1$ antes $$$m$ . Luego agregue los gradientes resultantes. El resultado de la suma será el mismo que si calculamos inmediatamente el gradiente de los índices desde el primero hasta $$$m$ . Por lo tanto, si los datos se distribuyen entre varias partes de los datos, el gradiente se puede calcular de forma independiente en cada parte, y luego los resultados de estos cálculos se pueden sumar para obtener el resultado final:

$$

$$\ nabla f (x) = \ sum_ {i \ en P_1} 2a_i (a_ix - b_i) + \ sum_ {i \ en P_2} 2a_i (a_ix - b_i) + ... + \ sum_ {i \ in P_k} 2a_i (a_ix - b_i)$$

En términos de implementación, esto encaja en el paradigma de MapReduce . En cada paso del descenso del gradiente, se envía una tarea para calcular el gradiente a cada nodo de datos, luego los gradientes calculados se recopilan juntos y el resultado de su suma se utiliza para mejorar el resultado.

A pesar de la simplicidad de implementación y la capacidad de ejecución en el paradigma de MapReduce, el descenso de gradiente también tiene sus inconvenientes. En particular, el número de pasos necesarios para lograr la convergencia es significativamente mayor en comparación con otros métodos más especializados.

LSQR

LSQR es otro método para resolver el problema, que es adecuado tanto para reconstruir la regresión lineal como para resolver sistemas de ecuaciones lineales. Su característica principal es que combina las ventajas de los métodos matriciales y un enfoque iterativo. Las implementaciones de este método se pueden encontrar tanto en la biblioteca SciPy como en MATLAB . Aquí no se proporcionará una descripción de este método (se puede encontrar en el artículo LSQR: Un algoritmo para ecuaciones lineales dispersas y mínimos cuadrados dispersos ). En cambio, se demostrará un enfoque para adaptar el LSQR a la ejecución en un entorno distribuido.

El método LSQR se basa en el procedimiento de bidiagonalización. Este es un procedimiento iterativo, cuya iteración consta de los siguientes pasos:


Pero basado en el hecho de que la matriz $$$A$ particionado horizontalmente, entonces cada iteración se puede representar como dos pasos MapReduce. Por lo tanto, es posible minimizar las transferencias de datos durante cada iteración (solo vectores con una longitud igual al número de incógnitas):



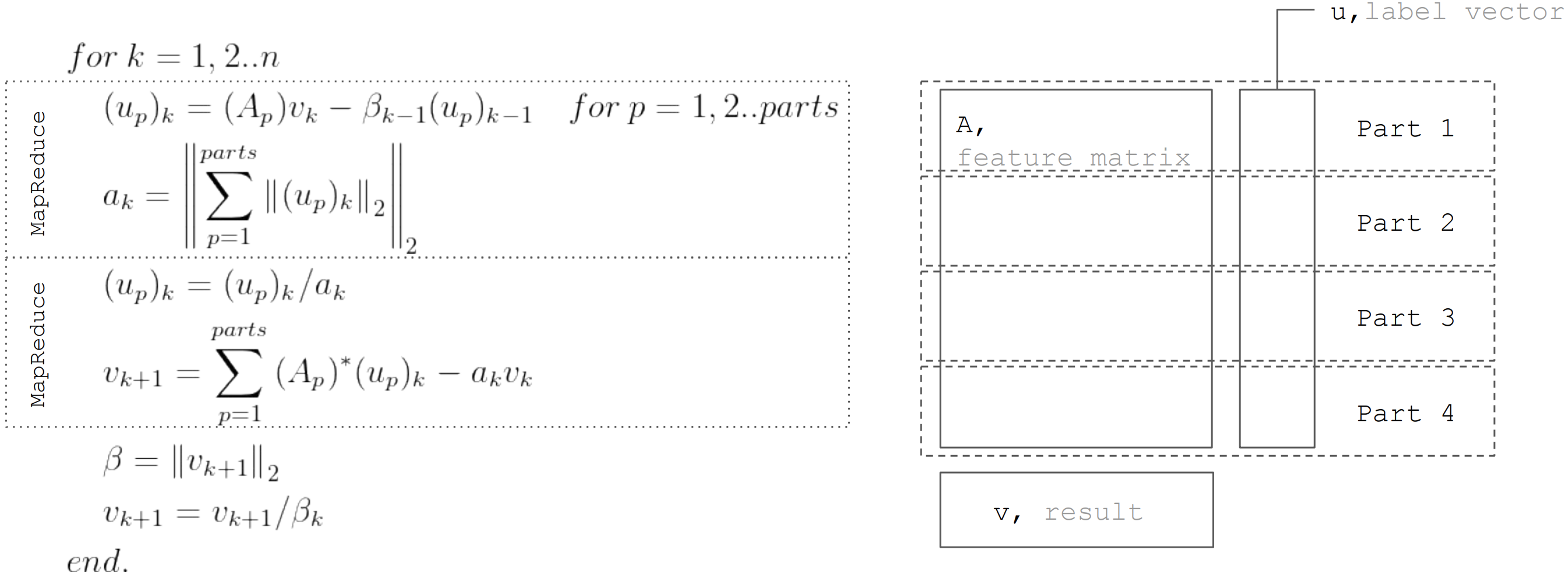
Este enfoque se utiliza al implementar la regresión lineal en Apache Ignite ML .

Conclusión

Existen muchos algoritmos de recuperación de regresión lineal, pero no todos pueden aplicarse en cualquier condición. Por lo tanto, la descomposición QR es ideal para una solución precisa en pequeños conjuntos de datos. El descenso de gradiente se implementa simplemente y le permite encontrar rápidamente una solución aproximada. Y LSQR combina las mejores propiedades de los dos algoritmos anteriores, ya que se puede distribuir, converge más rápido en comparación con el descenso de gradiente y también permite una detención temprana del algoritmo, a diferencia de la descomposición QR, para encontrar una solución aproximada.