En la mayoría de los sistemas de diseño (CAD), la representación principal del objeto simulado es la representación de límites de la geometría o B-rep (representación de límites). Pero cada vez más, los usuarios de CAD tienen que lidiar con modelos de polígonos, por ejemplo, obtenidos como resultado del escaneo 3D o tomados prestados de catálogos en línea.
Para que sean adecuados para el trabajo posterior, debe convertir la malla poligonal en un modelo B-rep. Y esto no es fácil.
Desarrollamos el componente de software C3D B-Shaper, que está integrado en el sistema de diseño y convierte los modelos poligonales en una representación de límites. En esta publicación mostraremos el algoritmo de conversión y ejemplos de implementación en C ++.




¿Cuál es el principal problema de los modelos poligonales en términos de CAD? No se les pueden aplicar las herramientas tradicionales: realizar operaciones booleanas, construir chaflanes y filetes, obtener proyecciones y secciones. Si usar el modelo B-rep para construir su representación poligonal es bastante fácil (esto se hace usando triangulación), entonces la transformación inversa es mucho más difícil. Surgen una serie de problemas: el reconocimiento de superficies de varios tipos (incluidas las superficies de forma libre), la presencia de ruido, que son característicos, por ejemplo, de los resultados de escaneo 3D.

En el nuevo SDK, implementamos un mecanismo de tres etapas para convertir el modelo poligonal en B-rep: segmentación, reconstrucción de superficie, construcción del modelo B-rep. En general, se supone que el proceso es iterativo: si por alguna razón el usuario no está satisfecho con el resultado, puede realizar los cambios correctivos necesarios en las etapas de segmentación y reconstrucción de las superficies.


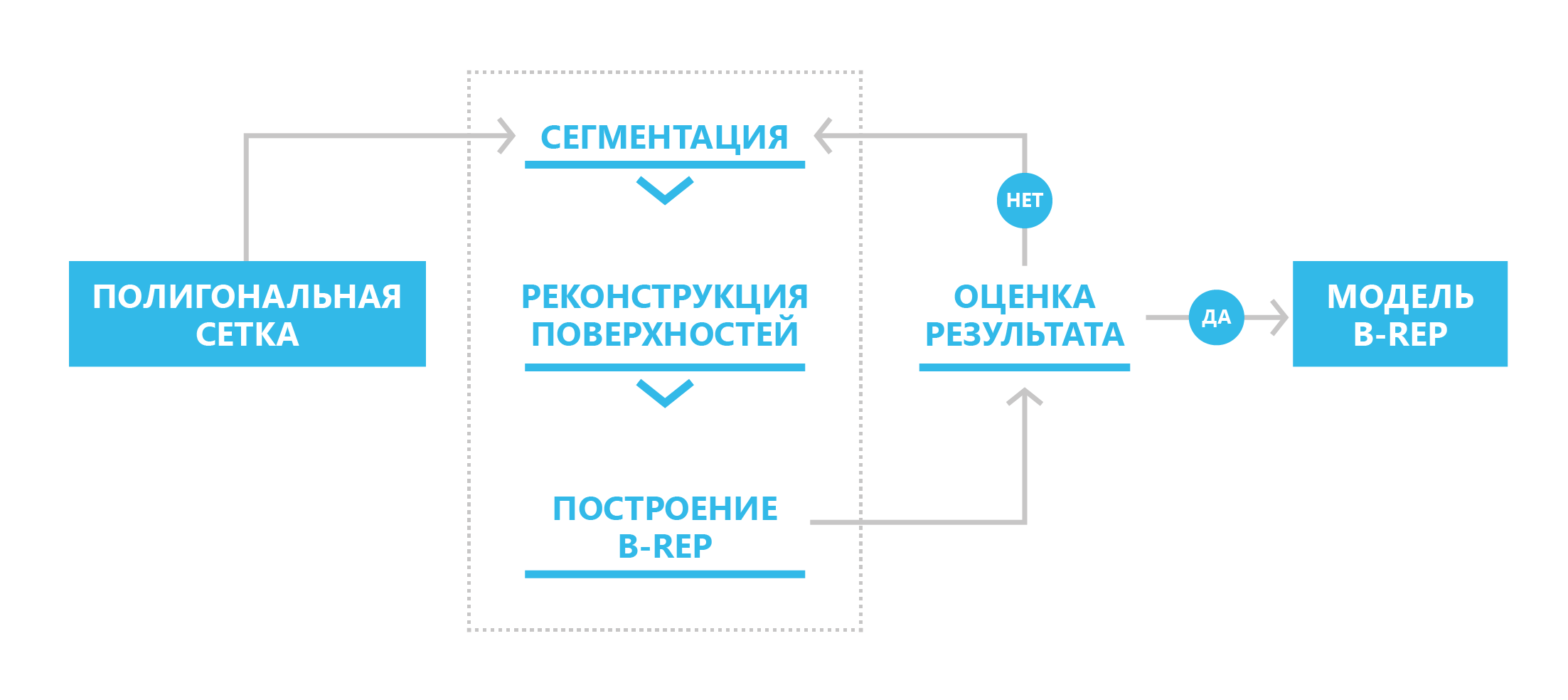El esquema para convertir una representación poligonal en un límite

Antes de iniciar el proceso de conversión a B-rep, es necesario, en algunos casos, mejorar la calidad de la malla poligonal original: coordine las direcciones de las normales en los polígonos vecinos, elimine los "agujeros", aplique algoritmos de suavizado en presencia de ruido en la malla original.

Segmentación poligonal

En la primera etapa, el conjunto inicial de polígonos de malla se clasifica en subconjuntos (segmentos). La información sobre las normales en los vértices de la malla permite la segmentación de primer orden y, por lo tanto, garantiza la partición inicial de la malla, así como también clasifica las áreas planas o fuertemente curvadas.

La malla inicial se basa en la definición de los llamados bordes "afilados", tales bordes entre dos polígonos triangulares cuyo ángulo entre las normales promedio excede un cierto valor predeterminado.

La segmentación de segundo orden analiza la cuadrícula de acuerdo con sus curvaturas principales, lo que proporciona una base suficiente para la clasificación de superficies elementales. Al calcular las curvaturas en los vértices de la cuadrícula, utilizamos los resultados de Mayer (Mark Meyer, Mathieu Desbrun, Peter Schroder y Alan H. Barr, Operadores discretos de geometría diferencial para colectores triangulares de 2, visualización y matemáticas III, 2003) para determinar el diferencial discreto operador para regiones trianguladas: para cada vértice de la malla original, consideramos un conjunto de vértices vecinos asociados con un vértice dado a través de un borde. Luego, se calcula un operador discreto K para un vértice dado, en base al cual se determinan la curvatura promedio normal, promedio K _H y Gaussiana K _G en el vértice de la cuadrícula.


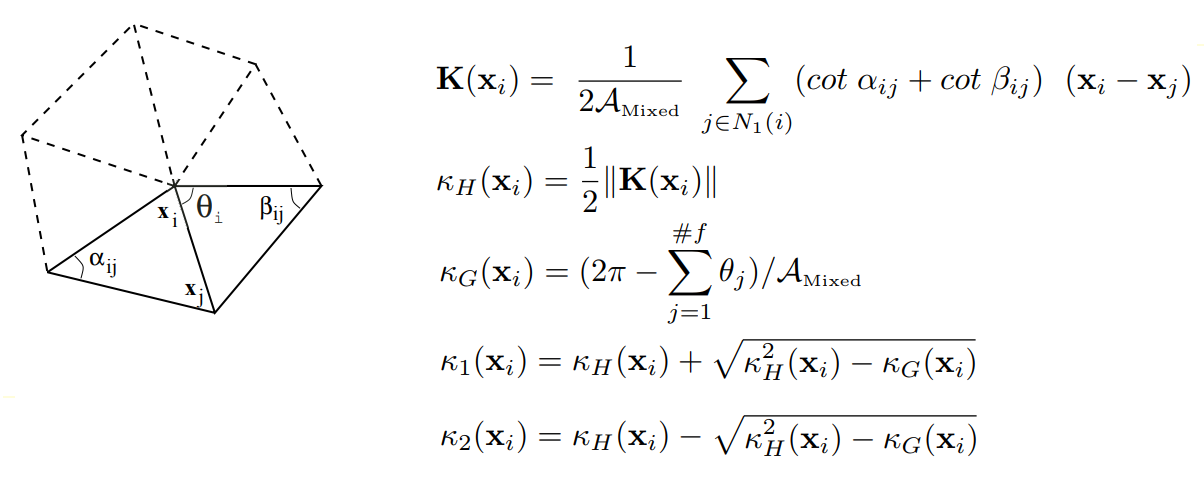Sobre la definición de un operador diferencial discreto para dominios triangulados

Por lo tanto, se calcula el tensor de curvatura para cada vértice de la cuadrícula, cuyos valores propios son las curvaturas principales deseadas K ₁ y K ₂ , y los vectores propios son las direcciones principales del cambio de curvatura.

A continuación, los vértices de malla se clasifican según los valores de las curvaturas principales K ₁ y K ₂ calculadas en ellos. El algoritmo de clasificación de vértices se basa en el método de k-medias, es decir, en minimizar la desviación cuadrática total de los puntos del grupo desde los centros de estos grupos. Como resultado, en la salida del algoritmo, cada vértice de la cuadrícula está asociado con un determinado grupo $$$Ci$y un par de curvaturas (centro del grupo) (L. Guillaume, "Segmentación de malla triangular basada en tensor de curvatura con rectificación de límites", Proceedings Computer Graphics International (CGI), 2004).


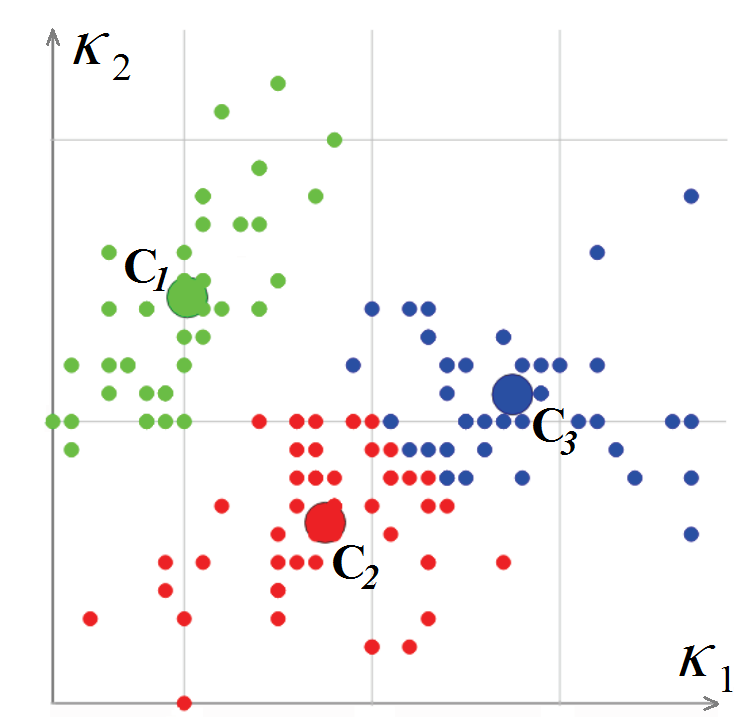Clasificación de los vértices de una malla poligonal en el espacio de curvaturas.

Después de clasificar los vértices de la malla poligonal, es necesario clasificar los polígonos. Al comienzo de este procedimiento, se selecciona un polígono triangular para el cual la curvatura puede considerarse completamente definida (los tres vértices pertenecen a un grupo o dos vértices se encuentran en un borde afilado). Este polígono se declara un nuevo segmento, y el procedimiento recursivo para expandir el segmento comienza a partir de él: para cada polígono triangular, se consideran los polígonos adyacentes a él, siempre que el borde entre ellos no sea "afilado".

Si el vértice de un polígono vecino, opuesto al borde común, se encuentra en un borde afilado o pertenece al mismo grupo, entonces este polígono se agrega al segmento. El proceso se repite hasta que se vean todos los polígonos de esta cuadrícula. Así es como se ve el mecanismo de segmentación de malla implementado.


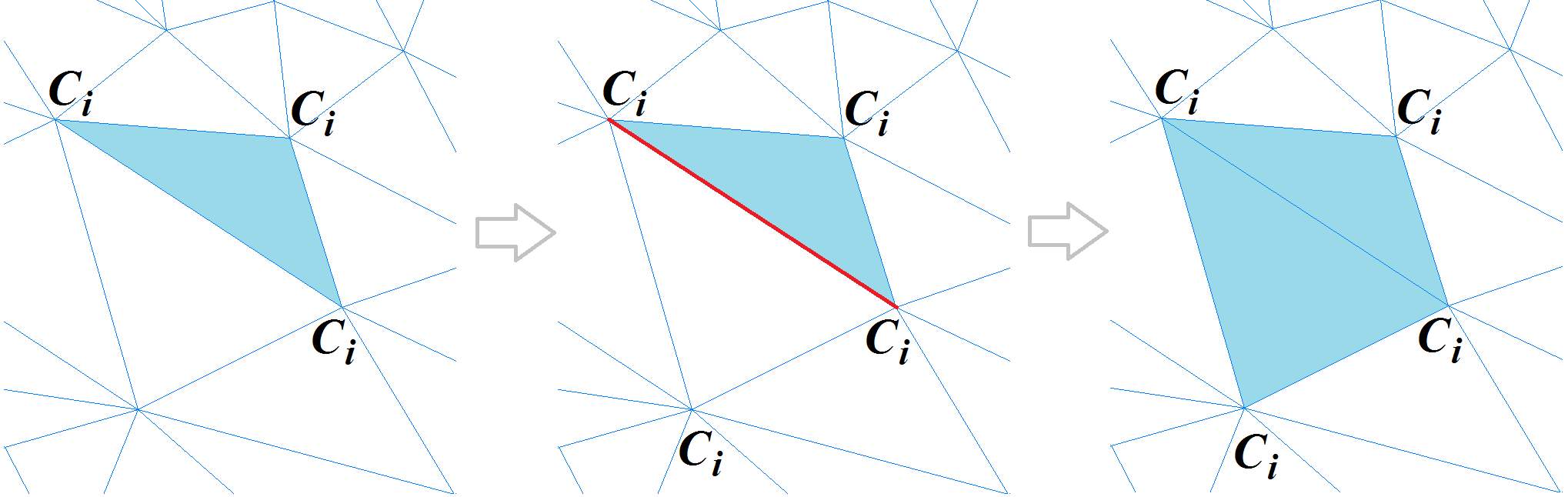Mecanismo de segmentación de malla poligonal

Al final del procedimiento de formación de segmentos, se realiza un algoritmo especial para unir segmentos adyacentes para eliminar la segmentación excesiva de la malla en cuestión.

Reconocimiento de superficie

En la segunda etapa, cada uno de los segmentos debe estar asociado con una determinada superficie que se aproxima a su forma con una precisión dada. En primer lugar, los valores de las curvaturas principales para un segmento determinado determinan la posibilidad de describir la forma de un segmento por una superficie elemental:

• plano: k ₁ = k ₂ = 0
• esfera: k ₁ = k ₂ = K > 0
• cilindro: k ₁ = K > 0, k ₂ = 0
• cono: k ₁ ∈ [ a , b ], k ₂ = 0
• toro: k ₁ = K , k ₂ ∈ [ a , b ]

Si ninguna de las superficies elementales es adecuada para describir un segmento, el algoritmo intentará reconocer la superficie de extrusión o rotación. Finalmente, si no fuera posible seleccionar una superficie analítica para describir la forma del segmento, se construirá una superficie NURBS para él.

Las superficies elementales se construyen utilizando métodos para ajustar objetos geométricos simples en un conjunto de puntos. Entonces, para ajustar el círculo y la esfera, se usa el método de mínimos cuadrados, para ajustar el plano, el método del componente principal. Se verifica que cada superficie reconstruida cumpla con un segmento para una precisión de reconocimiento dada.

Para mayor claridad, pintamos las superficies reconocidas en diferentes colores: planos - azul, cilindros - rojo, esferas - verde, conos - amarillo, tori - púrpura.


Malla poligonal original (izquierda) y malla segmentada (derecha) con superficies reconocidas en segmentos

Construyendo un Modelo B-rep

La etapa final de la transformación es la construcción de un modelo B-rep basado en la segmentación de las superficies reconocidas. En este enfoque, un gráfico de regiones adyacentes se construye sobre la base de regiones segmentadas, lo que refleja la topología del modelo y sirve como base para construir el modelo final de B-rep.

A diferencia de las etapas anteriores de conversión, el ensamblaje B-rep se lleva a cabo en un modo totalmente automático: se encuentran las líneas de intersección de las superficies reconstruidas adyacentes, los bordes de las caras se construyen sobre ellas, las caras mismas y, finalmente, se ensambla la carcasa B-rep.




Malla poligonal original (izquierda) y modelo B-rep (derecha)

Sin embargo, no siempre es posible construir un shell topológicamente correcto. Como ejemplo de tal situación, suponga que durante la reconstrucción de superficies tenemos dos superficies: un cilindro y un plano, y su posición en el espacio está cerca de la tangente. Debido a errores en la reconstrucción de las superficies de su intersección, puede que no haya ninguna. En tales casos, la carcasa puede construirse con algunos defectos que el usuario puede corregir ajustando adecuadamente los parámetros de la superficie.

Tipos de modelos poligonales y la elección del modo de conversión.

Hoy en día, existen varias fuentes principales de modelos en la representación poligonal:

• catálogos en línea, bases de datos de modelos 3D en formato poligonal (STL, VRML, OBJ), por ejemplo, 3D Warehouse, Cults 3D, etc.
• Resultados de escaneo 3D
• resultados de la optimización del modelo topológico por algoritmos CAE.

Los modelos poligonales de estas fuentes se pueden dividir en dos grupos: el primero incluye modelos que son triangulaciones de objetos B-rep, y el segundo, todos los demás. Las diferencias características del primer grupo son la ausencia de ruido en la malla poligonal y el predominio de superficies definidas analíticamente. Por lo tanto, la conversión a los modelos B-rep del primer grupo se realizará en modo totalmente automático o con una mínima intervención del usuario.

Las cuadrículas poligonales de los modelos del segundo grupo implican una interacción interactiva más densa con el usuario. Por lo tanto, inicialmente establecimos dos modos de funcionamiento en el C3D B-Shaper: totalmente automático e interactivo.

La elección de un modo particular también depende del propósito de la transformación: en algunos casos, la conectividad topológica de los elementos del shell resultante, así como su corrección, pueden descuidarse. Tal enfoque es aceptable, por ejemplo, para optimizar el renderizado en una aplicación BIM, cuando el usuario puede agregar elementos interiores arbitrarios al modelo actual de la sala. Por otro lado, para problemas de ingeniería inversa es necesario obtener la copia más precisa del modelo original, por ejemplo, para preservar la alineación de los cilindros con una precisión dada, para garantizar la ubicación tangente de un par de superficies y, como resultado, para obtener la topología correcta del modelo; en este caso, no puede prescindir de la intervención del usuario en proceso de conversión

La interfaz de conversión automática C3D B-Shaper está representada por las siguientes funciones, que aceptan la cuadrícula de entrada y la configuración de conversión como entrada:

MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params ); 

La configuración de conversión incluye el valor de precisión de reconocimiento, es decir La distancia máxima permitida de los vértices de la malla poligonal dentro de los límites de este segmento a la superficie reconocida. Esta precisión puede ser absoluta o relativa: cuando se usa la precisión relativa, la desviación de las caras del cuerpo de la cuadrícula se verifica con respecto al tamaño del modelo.

Además, el usuario tiene la opción de cambiar los modos de reconocimiento, lo que le permite controlar los tipos de superficies durante la reconstrucción.
La interfaz de clase MbMeshProcessor proporciona capacidades avanzadas para gestionar los procesos de segmentación y reconocimiento de superficie:

 class MbMeshProcessor { .. public: // “” . void SetUseMeshSmoothing( bool useSmoothing ); //   . const MbCollection & GetSegmentedMesh(); MbResultType SegmentMesh( bool createSurfaces = true ); void ResetSegmentation(); void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx ); MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep ); //   . void FitSurfaceToSegment( size_t idxSegment ); void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType ); const MbSurface * GetSegmentSurface( size_t idxSegment ) const; //  B-rep . MbResultType CreateBRepShell( MbFaceShell *& pShell ); .. } 

Por ejemplo, para corregir los resultados de la segmentación automática, se proporcionan herramientas para combinar segmentos, separarlos, etc. El usuario puede ingresar una superficie de un tipo dado en un segmento, así como cambiar los parámetros para una superficie ya reconocida.

Que esta pasando ahora

En julio, lanzamos la primera versión del componente y ahora continuamos desarrollándonos en varias áreas: algoritmos de segmentación automática, herramientas de edición de segmentación, construcción de superficies de forma libre (NURBS) basadas en un segmento y mejora de la calidad de construcción de los depósitos B-rep.

Los desarrolladores interesados ​​pueden probar el C3D B-Shaper. El componente se proporciona de forma gratuita durante tres meses previa solicitud en nuestro sitio web.

Autor - Andrey Tumanin, Ph.D., matemático-programador de C3D Labs