
Uno de los recursos más valiosos de cualquier red social es el "gráfico de las amistades": la información se difunde a través de las conexiones en esta columna, se envía contenido interesante a los usuarios y se envían comentarios constructivos a los autores del contenido. Además, el gráfico también es una fuente importante de información que le permite comprender mejor al usuario y mejorar continuamente el servicio. Sin embargo, en los casos en que el gráfico crece, técnicamente es cada vez más difícil extraer información del mismo. En este artículo hablaremos sobre algunos trucos utilizados para procesar gráficos grandes en OK.ru.
Para comenzar, considere una tarea simple del mundo real: determinar la edad del usuario. Conocer la edad permite a la red social seleccionar contenido más relevante y adaptarse mejor a la persona. Parece que la edad ya está indicada al crear una página en las redes sociales, pero de hecho, con bastante frecuencia, los usuarios son astutos e indican una edad diferente de la real. Un gráfico social puede ayudar a rectificar la situación :).
Tomemos, por ejemplo, Bob (todos los personajes del artículo son ficticios, cualquier coincidencia con la realidad es el resultado de la creatividad de una casa al azar):

Por un lado, la mitad de los amigos de Bob son adolescentes, lo que sugiere que Bob también es un adolescente. Pero también tiene amigos mayores, por lo que la confianza en la respuesta es baja. La información adicional del gráfico social puede ayudar a aclarar la respuesta:

Al tener en cuenta no solo los arcos en los que Bob está directamente involucrado, sino también los arcos entre sus amigos, podemos ver que Bob es parte de una densa comunidad de adolescentes, lo que nos permite llegar a una conclusión sobre su edad con un mayor grado de confianza.
Dicha estructura de datos se conoce como una red del ego o subgrafo del ego; durante mucho tiempo se ha utilizado con éxito para resolver muchos problemas: búsqueda de comunidades, identificación de bots y spam, recomendaciones de amigos y contenido, etc. Sin embargo, el cálculo del ego de una subgrafía para todos los usuarios en un gráfico con cientos de millones de nodos y decenas de miles de millones de arcos está plagado de una serie de "pequeñas dificultades técnicas" :).
El principal problema es que al considerar la información sobre el "segundo paso" en el gráfico, se produce una explosión cuadrática del número de conexiones. Por ejemplo, para un usuario con 150 enlaces directos del ego, una subgrafía puede incluir hasta 150+150∗149/2=$11,32 enlaces, y para un usuario activo con 5,000 amigos, el subgrafo del ego puede crecer a más de 12,000,000 enlaces.
Una complicación adicional es el hecho de que el gráfico se almacena en un entorno distribuido y ningún nodo tiene una imagen completa del gráfico en la memoria. El trabajo en la partición equilibrada de gráficos se lleva a cabo tanto en la academia como en la industria, pero incluso los mejores resultados al recopilar el subgrafo del ego conducen a la comunicación "todos con todos": para obtener información sobre los amigos de los amigos del usuario, tendrá que ir a todas las "particiones" en la mayoría de los casos
Una de las alternativas de trabajo en este caso será la duplicación forzada de datos (por ejemplo, el algoritmo 3 en un artículo de Google ), pero esta duplicación tampoco es gratuita. Tratemos de descubrir qué se puede mejorar en este proceso.
Algoritmo ingenuo
Para comenzar, considere el algoritmo "ingenuo" para generar un subgráfico del ego:

El algoritmo supone que el gráfico original se almacena como una lista de adyacencia, es decir. La información sobre todos los amigos del usuario se almacena en un solo registro con la ID de usuario en la clave y la lista de ID de amigos en el valor. Para dar el segundo paso y obtener información sobre amigos que necesita:
- Convierta un gráfico en la lista de aristas, donde cada arista es una entrada separada.
- Haga que la lista de aristas se una sobre sí misma, lo que dará todas las rutas en un gráfico de longitud 2.
- Agrupar por inicio de ruta.
En la salida para cada usuario, obtenemos listas de rutas de longitud 2 para cada usuario. Cabe señalar aquí que la estructura resultante es en realidad una vecindad de dos pasos del usuario , mientras que la subgrafía del ego es su subconjunto. Por lo tanto, para completar el proceso, debemos filtrar todos los arcos que salen de los amigos inmediatos.
Este algoritmo es bueno porque se implementa en dos líneas en Scala bajo Apache Spark . Pero las ventajas terminan ahí: para un gráfico de tamaño industrial, el volumen de comunicación de la red está más allá del límite y el tiempo de operación se mide en días. La principal dificultad es creada por dos operaciones de barajado que ocurren cuando unimos y agrupamos. ¿Es posible reducir la cantidad de datos enviados?
Subgrafo del ego en una barajadura
Dado que nuestro gráfico de amistades es simétrico, puede usar las optimizaciones propuestas por Tomas Schank :
- Puede obtener todos los caminos de longitud 2 sin unirse: si Bob tiene amigos Alice y Harry, entonces hay caminos Alice-Bob-Harry y Harry-Bob-Alice.
- Al agrupar, dos caminos en la entrada corresponden al mismo borde nuevo. La ruta Bob-Alice-Dave y Bob-Dave-Alice contiene la misma información para Bob, lo que significa que puede enviar solo cada segunda ruta, clasificando a los usuarios por su ID.
Después de aplicar las optimizaciones, el esquema de trabajo se verá así:

- En la primera etapa de generación, obtenemos una lista de rutas de longitud 2 con un filtro de ID de pedido.
- En el segundo, nos agrupamos por el primer usuario en el camino.
En esta configuración, el algoritmo cumple una operación aleatoria y el tamaño de los datos transmitidos por la red se reduce a la mitad. :)
Coloca el subgrafo del ego en la memoria
Una cuestión importante que aún no hemos considerado es cómo descomponer los datos en el ego de un subgráfico en la memoria. Para almacenar el gráfico como un todo, utilizamos una lista de adyacencia. Esta estructura es conveniente para tareas en las que es necesario pasar por el gráfico terminado en su conjunto, pero es costoso si queremos construir un gráfico a partir de piezas y hacer análisis más sutiles. La estructura ideal para nuestra tarea debe realizar efectivamente las siguientes operaciones:
- La unión de dos gráficos obtenidos de diferentes particiones.
- Conseguir todos los amigos humanos.
- Comprobando si dos personas están conectadas.
- Almacenamiento en memoria sin gastos generales de boxeo.
Uno de los formatos más adecuados para estos requisitos es el análogo de una matriz de CSR dispersa :
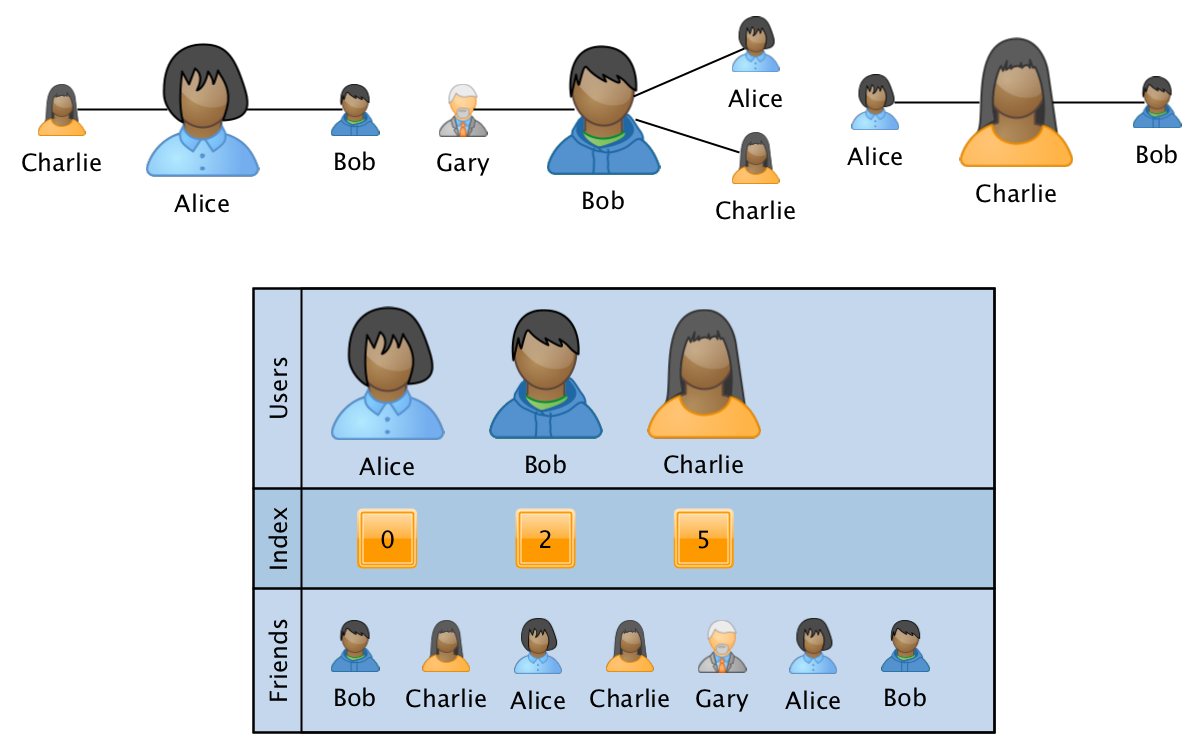
El gráfico en este caso se almacena en forma de tres matrices:
- usuarios: una matriz ordenada con la ID de todos los usuarios que participan en el gráfico.
- index: una matriz del mismo tamaño que los usuarios, donde para cada usuario se almacena un puntero de índice al comienzo de la información sobre las relaciones de los usuarios en la tercera matriz.
- amigos: una matriz de tamaño igual al número de bordes en el gráfico, donde los ID de los usuarios relacionados se muestran secuencialmente para los ID correspondientes de los usuarios. La matriz se ordena por velocidad de procesamiento dentro de la información sobre los enlaces de un solo usuario.
En este formato, la operación de fusionar dos gráficos se realiza en tiempo lineal, y la operación de obtener información sobre un usuario específico o sobre un par de usuarios por logaritmo del número de vértices. En este caso, la sobrecarga en la memoria no depende del tamaño del gráfico, ya que se utiliza un número fijo de matrices. Al agregar una cuarta matriz de datos de tamaño igual al tamaño de los amigos, puede guardar información adicional asociada con las relaciones en el gráfico.
Usando la propiedad de simetría de gráfico, puede almacenar solo la mitad de los arcos "triangulares superiores" (cuando los arcos se almacenan solo de una ID más pequeña a una más grande), pero en este caso, la reconstrucción de todas las conexiones de un solo usuario llevará tiempo lineal. Un buen compromiso en este caso puede ser un enfoque que utiliza la codificación "triangular superior" para el almacenamiento y la transferencia entre nodos, y la codificación simétrica al cargar el ego del subgrafo en la memoria para su análisis.
Reducir barajar
Sin embargo, incluso después de implementar toda la optimización mencionada anteriormente, la tarea de construir todas las subgrafías del ego todavía funciona demasiado tiempo. En nuestro caso, aproximadamente 6 horas con una alta utilización del clúster. Una mirada más cercana muestra que la principal fuente de complejidad sigue siendo la operación de barajar, mientras que una parte importante de los datos involucrados en la baraja se descarta en las siguientes etapas. El hecho es que el enfoque descrito construye una vecindad completa de dos pasos para cada usuario, mientras que el subgrafo del ego es solo un subconjunto relativamente pequeño de esta vecindad que contiene solo arcos internos .
Por ejemplo, si al procesar a los vecinos directos de Bob, Harry y Frank, supiéramos que no eran amigos, entonces, en el primer paso, podríamos filtrar esos caminos externos. Pero para saber si Gary y Frenkov son amigos, tendrá que arrastrar el gráfico de amistad a la memoria en todos los nodos informáticos o realizar llamadas remotas mientras procesa cada registro, lo que, según las condiciones de la tarea, es imposible.
Sin embargo, existe una solución si nos permitimos, en un pequeño porcentaje de casos, cometer errores cuando encontramos amistad donde realmente no existe. Hay toda una familia de estructuras de datos probabilísticas que permiten reducir el consumo de memoria durante el almacenamiento de datos en órdenes de magnitud, al tiempo que permiten una cierta cantidad de error. La estructura más famosa de este tipo es el filtro Bloom , que durante muchos años se ha utilizado con éxito en bases de datos industriales para compensar las fallas en el caché de "cola larga".
La tarea principal del filtro Bloom es responder la pregunta "¿está incluido este elemento en los muchos elementos vistos anteriormente?" Además, si el filtro responde "no", entonces el elemento probablemente no esté incluido en el conjunto, pero si responde "sí", existe una pequeña probabilidad de que el elemento todavía no esté allí.
En nuestro caso, el "elemento" será un par de usuarios, y el "conjunto" será todos los bordes del gráfico. Luego, el filtro Bloom se puede aplicar con éxito para reducir el tamaño de la mezcla aleatoria:

Una vez preparado el filtro Bloom con información sobre el gráfico, podemos mirar a través de los amigos de Harry para descubrir que Bob e Ilona no son amigos, lo que significa que no necesitamos enviarle información sobre la conexión entre Gary e Ilona. Sin embargo, la información de que Harry y Bob son amigos por sí solos aún tendrá que enviarse para que Bob pueda restaurar completamente su gráfica de amistad después de la agrupación.
Eliminar barajar
Después de aplicar el filtro, la cantidad de datos enviados se reduce en aproximadamente un 80%, y la tarea se completa en 1 hora con una carga de clúster moderada, lo que le permite realizar libremente otras tareas en paralelo. En este modo, ya se puede "poner en funcionamiento" y poner a diario, pero todavía hay potencial para la optimización.
Por paradójico que pueda parecer, el problema puede resolverse sin recurrir a la combinación aleatoria, si se permite un cierto porcentaje de errores. Y el filtro Bloom puede ayudarnos con esto:

Si miramos la lista de amigos de Bob usando un filtro, descubrimos que Alice y Charlie son casi seguramente amigos, podemos agregar inmediatamente el arco correspondiente al subgrafo del ego de Bob. Todo el proceso en este caso tomará menos de 15 minutos y no requerirá la transferencia de datos a través de la red, sin embargo, un cierto porcentaje de arcos, dependiendo de la configuración del filtro, puede estar ausente en la realidad.
Los arcos adicionales agregados por el filtro no introducen distorsiones significativas para algunas tareas: por ejemplo, al contar triángulos, podemos corregir fácilmente el resultado, y al preparar atributos para algoritmos de aprendizaje automático, la corrección ML en sí misma se puede aprender en el siguiente paso.
Pero en algunas tareas, los arcos adicionales conducen a un deterioro fatal en la calidad del resultado: por ejemplo, cuando se buscan componentes conectados en el subgrafo del ego con un ego remoto (sin la parte superior del usuario), la probabilidad de un "puente fantasma" entre los componentes aumenta cuadráticamente en relación con su tamaño, lo que conduce a que en casi todas partes tenemos un gran componente.
Hay un área intermedia donde el efecto negativo de los arcos adicionales debe evaluarse experimentalmente: por ejemplo, algunos algoritmos de búsqueda de la comunidad pueden hacer frente con bastante éxito a un poco de ruido, devolviendo una estructura comunitaria casi idéntica.
En lugar de una conclusión
Las subgrafías de usuarios del ego son una fuente importante de información que se utiliza activamente en OK para mejorar la calidad de las recomendaciones, refinar la demografía y combatir el correo no deseado, pero su cálculo está plagado de una serie de dificultades.
En el artículo, examinamos la evolución del enfoque de la tarea de construir subgrafos del ego para todos los usuarios de una red social y pudimos mejorar el tiempo de trabajo desde las 20 horas iniciales hasta 1 hora, y en el caso de un pequeño porcentaje de errores, hasta 10-15 minutos.
Los tres "pilares" en los que se basa la decisión final son:
- Usando la propiedad de simetría gráfica y los algoritmos de Tomas Schank .
- Almacene eficientemente las subgrafías del ego utilizando una matriz de CSR dispersa .
- Use un filtro Bloom para reducir la transferencia de datos a través de la red.
Se pueden encontrar ejemplos de cómo ha evolucionado el código del algoritmo en el cuaderno Zeppelin .