En Habré ya había muchos artículos dedicados a cálculos rápidos de trigonometría cuando es muy necesario, pero me gustaría complementarlos con una pequeña nota con referencia a la trigonometría escolar.
A veces puede no haber una implementación de hardware de trigonometría, a veces puede haber otras razones para inventar métodos para acelerar el cálculo.
Matemáticas
Recordemos algunas fórmulas simples del curso escolar.
Comencemos con los simples:
(1)
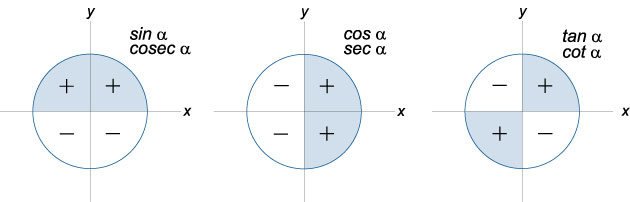
sin x = cos (90° - x)cos x = sin (90° - x)sin -x = -sin xcos -x = cos x- En el caso general,
sin (90°N ± x) = ±cos x para N impar y ±sin x para par. El signo se toma en función del signo del argumento en el cuarto correspondiente del círculo.
Siguiente:
(2)
cos (x + y) = cos x cos y - sin x sin ysin (x + y) = sin x cos y + cos x sin y
Y también:
(3)
sin x = x - x^3/3! + x^5/5! - ...cos x = 1 - x^2/2! + x^4/4! - ...
El coseno / seno de cualquier ángulo se puede reducir a un argumento en el rango de 0 ° a 45 ° usando las fórmulas del primer grupo.
Para ángulos pequeños, las funciones trigonométricas pueden reducirse a expansiones asintóticas si los términos descartados van más allá de la rejilla de descarga.
Todos los ángulos intermedios se pueden obtener sumando ángulos grandes con un cierto paso (y para ellos la trigonometría se puede considerar tabular), y los residuos que tarde o temprano darán una descomposición lineal.
Solicitud
Supongamos que estamos trabajando con números de precisión individuales IEEE-754, tienen los nombres flotante, único, etc. Hay 23 caracteres en la mantisa, lo que significa que necesitamos obtener un error relativo de 2^-23 .
Evaluémos qué tan profundo necesita descender para construir tablas de argumentos.
Para el seno, descartamos el término cúbico, por lo que necesitamos que su relación con el lineal sea menor que el error permitido, lo que significa que: 1 - (x - x^3/3!) / x = x^2/6 2/6 2 ^ -23, de donde se deduce que para argumentos de no más de 0.000846 radianes, la precisión del cálculo aproximado para el seno es suficiente para nosotros. Para el coseno, si elimina el término cuadrático, necesita una precisión de aproximadamente 2 veces mejor: 0.000488 radianes.
Por lo tanto, no necesitamos tener valores tabulares para el argumento inferior a 0,000488 radianes.
Para construir la tabla, renormalice el argumento de entrada para que el valor 0 corresponda a un ángulo de 0 °, y para un valor de 1 corresponda a un ángulo de 45 °, o pi/4=0.78539816 radianes. Luego, el ángulo mínimo obtenido anteriormente se convertirá a 0.0006217 radianes, o aproximadamente 1/1600 , esto es más de 1/2048 = 2^-11 .
A continuación, deberá elegir el paso de las tablas en función de cómo queremos distribuir los cálculos, dividiremos el exponente 11 en varias partes. Por ejemplo, puede dividirlo en dos partes: 11 = 6 + 5, luego necesitamos dos tablas de tamaño 64 y 32 registros (total 96), o tres partes: 11 = 4 + 4 + 3 (tamaño de tabla 16 + 16 + 8 = 40 entradas), pero habrá más operaciones de multiplicación: la elección específica dependerá de la tarea y los recursos disponibles.
Nota: una entrada de tabla es un par de argumentos seno y coseno. Si se almacena con precisión simple, el tamaño del registro es de 8 bytes.
Ejemplo
Tomemos la descomposición 4 + 4 + 3 como ejemplo, y luego generalicemos.
Entonces, la tarea: calcular el valor de sin x para una x arbitraria.
Paso 1. Traemos el argumento x a nuestra escala, dividiéndolo por la constante pi/4 (llamémoslo x' ).
Paso 2. Dependiendo del valor del argumento x' usando las fórmulas (1), seleccionamos la función deseada para que su argumento esté en el rango de 0 a 1 (inclusive) (llamemos x'' . En este paso, también deberá marcar el signo del resultado .
[supongamos, por ejemplo, que el seno es]
Paso 3. Usaremos las tablas (te recordaré que hay 3 de ellas), mientras que los índices en la tabla serán "campos de bits" en la representación binaria del argumento x'' - los primeros 4 bits después del punto decimal, luego 4 más y 3 más, y los restantes para los negocios los bits irán al resto.
El seno de la tabla se llama S1, S2, S3, los cosenos de la tabla son C1, C2, C3.
Como dividimos el ángulo por pi/4 , para obtener el resto en radianes, debe multiplicarse por la misma cantidad. El resto "bit" multiplicado por pi/4 se denota por A. Entonces su seno será igual a A, y el coseno - 1.
Paso 4. Combina todo lo que sucedió:
C12 = C1 C2 - S1 S2 S12 = S1 C2 + C1 S2 C123 = C12 C3 - S12 S2 S123 = S12 C3 + C12 S3
|sin x| = S123 + C123 A |sin x| = S123 + C123 A (si obtuvo un seno en el paso 2)
|sin x| = C123 - S123 A |sin x| = C123 - S123 A (si recibió el coseno en el paso 2)
Paso 5. Si en el paso 2 consideramos que el resultado debería ser negativo, entonces este menos debería ingresarse en el resultado.
Conclusión
Se puede usar un enfoque similar tanto para calcular en números reales de cualquier tamaño como, por ejemplo, para implementar aritmética especializada de punto fijo. En realidad, en un momento fue solo la última tarea que me hizo profundizar en esta dirección, pero eso fue hace mucho tiempo.