Crecimiento. Peso. Tres vecinos

En busca de un conjunto de datos simple e interesante, me encontré con este hombre guapo .

Acerca de esta belleza

Contiene datos sobre el crecimiento y el peso de 10,000 hombres y mujeres . Sin descripción Nada "superfluo". Solo altura, peso y marca de piso. Me gustó esta misteriosa simplicidad.

Bueno, empecemos!

¿Qué fue interesante para mí?

• ¿Cuál es el rango de peso y altura para la mayoría de los hombres y mujeres?
• ¿Qué tipo de hombre "promedio" y mujer "promedio" son?
• ¿Puede el modelo simple de aprendizaje automático KNN de estos datos predecir peso por altura ?

Vamos!

Primer vistazo

Primero, cargue los módulos necesarios

#      import pandas as pd #     import matplotlib.pyplot as plt %matplotlib inline #    «  » from sklearn.neighbors import KNeighborsRegressor #         from sklearn.model_selection import train_test_split 

Cuando las bibliotecas se pusieron de pie exactamente, era hora de cargar el DataSet en sí y mirar los primeros 10 elementos. Esto es necesario para que nuestro intestino esté tranquilo, que hayamos cargado todo correctamente.

Por cierto, no se alarme de que la altura y el peso difieran de lo que estamos acostumbrados. Esto se debe a un sistema de medición diferente: pulgadas y libras , en lugar de centímetros y kilogramos .

 data = pd.read_csv('weight-height.csv') data.head(10) 

Bueno! Vemos que las primeras diez entradas son "hombres". Vemos su altura y peso . Los datos se cargaron bien.

Ahora puede ver el número de filas en el conjunto.

 data.shape >> (10000, 3) 

Diez mil líneas / registros. Y cada uno tiene tres parámetros . Lo que necesitas!

Es hora de arreglar el sistema de medición. Ahora aquí hay centímetros y kilogramos.

 data['Height'] *= 2.54 data['Weight'] /= 2.205 #    data.head(10) 

Ahora se ha vuelto más familiar. Y el primer registro nos cuenta sobre un hombre con una altura de ~ 190 cm y un peso de ~ 110 kg. Hombre grande. Llamémoslo Bob.

Pero cómo entenderlo: ¿es mucho o poco en comparación con el resto? ¿Es posible que todos seamos más o menos frijoles? Esto es un poco más tarde.

Ahora descubramos qué tan simétricos son los dos géneros en este conjunto de datos.

 data['Gender'].value_counts() >> Male 5000 Female 5000 Name: Gender, dtype: int64 

Idealmente dividido equitativamente. Y esto es bueno, porque si hubiera: 9999 hombres y 1 mujer, entonces no tendría sentido pretender que este DataSet revela ambos sexos igualmente bien. En nuestro caso, ¡todo está bien!

¡Divide y aprende!

Ahora la intuición sugiere que será correcto separar los dos sexos y explorar por separado. De hecho, en la vida a menudo vemos que los hombres y las mujeres tienen más o menos diferentes alturas y pesos

 #  data_male = data[data['Gender'] == 'Male'].copy() #  data_female = data[data['Gender'] == 'Female'].copy() 

Echemos un vistazo a las pequeñas estadísticas descriptivas que nos ofrece el módulo pandas .

Hombres :

 data_male.describe() 

Mujeres :

 data_female.describe() 

Vemos que en los hombres el promedio y la mediana son 175cm y 85kg. Y en mujeres : 162cm y 62kg. Esto nos dice que no hay emisiones fuertes. O son simétricos en ambos lados de la mediana. Lo cual es muy raro.

Pero ambos sexos tienen ligeras desviaciones de la media de la mediana. Pero son insignificantes y solo son visibles en centésimos. ¡Sigamos adelante!

Histograma

Este es un gráfico que traza los valores de mínimo a máximo en orden de crecimiento y muestra el número de instancias individuales.

 fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label='Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha=0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'], label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc=2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show() 

Los datos se distribuyen en forma de campana. Muy similar a la distribución normal .

Además de las pruebas estadísticas para la distribución normal, hay una prueba visual. Si la distribución por tipo y lógica parece ser normal, podemos suponer con algunos supuestos que estamos tratando con ella.

Se podría hacer una prueba de normalidad estadística y determinar el valor p, pero No puedo Esto está más allá del alcance del artículo.

Aprendiendo a trabajar con bolígrafos

Los pandas pueden contar mucho para nosotros. Pero necesita contar al menos una vez algunas estadísticas usted mismo. Ahora mostraré cómo calcular la desviación estándar .

Hagámoslo con el ejemplo de los hombres y la característica: crecimiento.

Media

Formula

$$

$$M = \ frac {1} {N} \ sum \ limits_ {i = 1} ^ N n_i$$

donde

• M - valor promedio
• N es el número de instancias
• ni - instancia única

Código:

 mean = data_male['Height'].mean() print('mean:\t{:.2f}'.format(mean)) >> mean: 175.33 

Altura media: 175 cm.

Desviación al cuadrado

$$

$$d_i = (n_i - M) ^ 2$$

donde

• di - desviación simple
• ni - instancia única
• M - promedio

Código:

 data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64 

Dispersión

Formula

$$

$$D = \ frac {1} {N} \ sum \ limits_ {i = 1} ^ N d_i$$

donde

• D es el valor de dispersión
• di - desviación simple
• N es el número de instancias

Código:

 disp = data_male['Height_d'].mean() print('disp:\t{:.2f}'.format(disp)) >> disp: 52.89 

Dispersión - 53

Desviacion estandar

Formula

$$

$$std = \ sqrt {D}$$

donde

• std - valor de desviación estándar
• D es el valor de dispersión

Código:

 std = disp ** 0.5 print('std:\t{:.2f}'.format(std)) >> std: 7.27 

Desviación Estándar - 7

Intervalos de confianza

Ahora descubriremos en qué rangos de crecimiento y peso se encuentran el 68%, el 95% y el 99.7% de los hombres y mujeres .

Esto no es tan difícil: debe sumar y restar la desviación estándar del promedio. Se ve así:

• 68% - más o menos una desviación estándar
• 95% - más o menos dos desviaciones estándar
• 99.7% - más o menos tres desviaciones estándar

Escribimos una función auxiliar que considerará esto:

 def get_stats(series, title='noname'): #    print('= {} =\n'.format(title.upper())) #     pandas descr = series.describe() #   mean = descr['mean'] print('= Mean:\t{:.0f}'.format(mean)) #    std = descr['std'] print('= Std:\t{:.0f}'.format(std)) #    print('\n= = = =\n') #   ## 68% devi_1 = [mean - std, mean + std] ## 95% devi_2 = [mean - 2 * std, mean + 2 * std] ## 99.7% devi_3 = [mean - 3 * std, mean + 3 * std] #   print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1])) print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1])) print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1])) 

Bueno, aplícalo a los datos:

Hombres | Crecimiento

 get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197 

Hombres | Peso

 get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112 

Mujeres | Crecimiento

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182 

Mujeres | Peso

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87 

De ahí las conclusiones:

• La mayoría de los hombres: 154cm - 197cm y 58kg - 112kg.
• La mayoría de las mujeres: 141cm - 182cm y 36kg - 87kg.

Ahora solo queda aplicar el aprendizaje automático a este conjunto e intentar predecir el peso por altura.

Vecinos más cercanos

El algoritmo "A los vecinos más cercanos" es simple. Existe para tareas de clasificación, para distinguir un gato de un perro, y para tareas de regresión, para adivinar el peso por altura. ¡Esto es lo que necesitamos!

Para la regresión, usa el siguiente algoritmo:

• Recuerda todos los puntos de datos.
• Cuando aparece un nuevo punto, busca K sus vecinos más cercanos (el usuario establece el número K)
• Promedia el resultado
• Da una respuesta

Primero debe dividir el conjunto de datos en las partes de entrenamiento y prueba y probar el algoritmo

Experimentando con hombres

 X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight']) 

Dividido, es hora de intentarlo.

 #   knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8298400793623182 #   knr5 = KNeighborsRegressor(n_neighbors=5) knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7958051642678619 #   knr7 = KNeighborsRegressor(n_neighbors=7) knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7769249318420969 

No iremos lejos y nos detendremos en tres vecinos. Pero la pregunta es: ¿puede un modelo así adivinar mi peso?

 knr3.predict([[180]])[0, 0] >> 88.67596236265881 

88kg está muy cerca. En este segundo, mi peso es de 89.8 kg

Cuadro de predicción para hombres

El momento de construir mi parte favorita de la ciencia son los gráficos.

 array_male = [] #   99.7% xaxis = range(154, 198) for h in xaxis: ans = knr3.predict([[h]]) array_male.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male, 'r-', linewidth=4) plt.title('Male heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_male.png') plt.show() 

Modelo y cuadro de predicción para mujeres

 X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight']) knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8135681584074799 

 array_female = [] #   99.7% xaxis = range(141, 183) for h in xaxis: ans = knr3.predict([[h]]) array_female.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_female, 'b-', linewidth=4) plt.title('Female heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_female.png') plt.show() 

Y, por supuesto, es interesante cómo se ven estos gráficos juntos:

 #      xaxis = range(154, 183) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4) plt.plot(xaxis, array_female[13:], 'b-', linewidth=4) plt.title('Together heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_together.png') plt.show() 

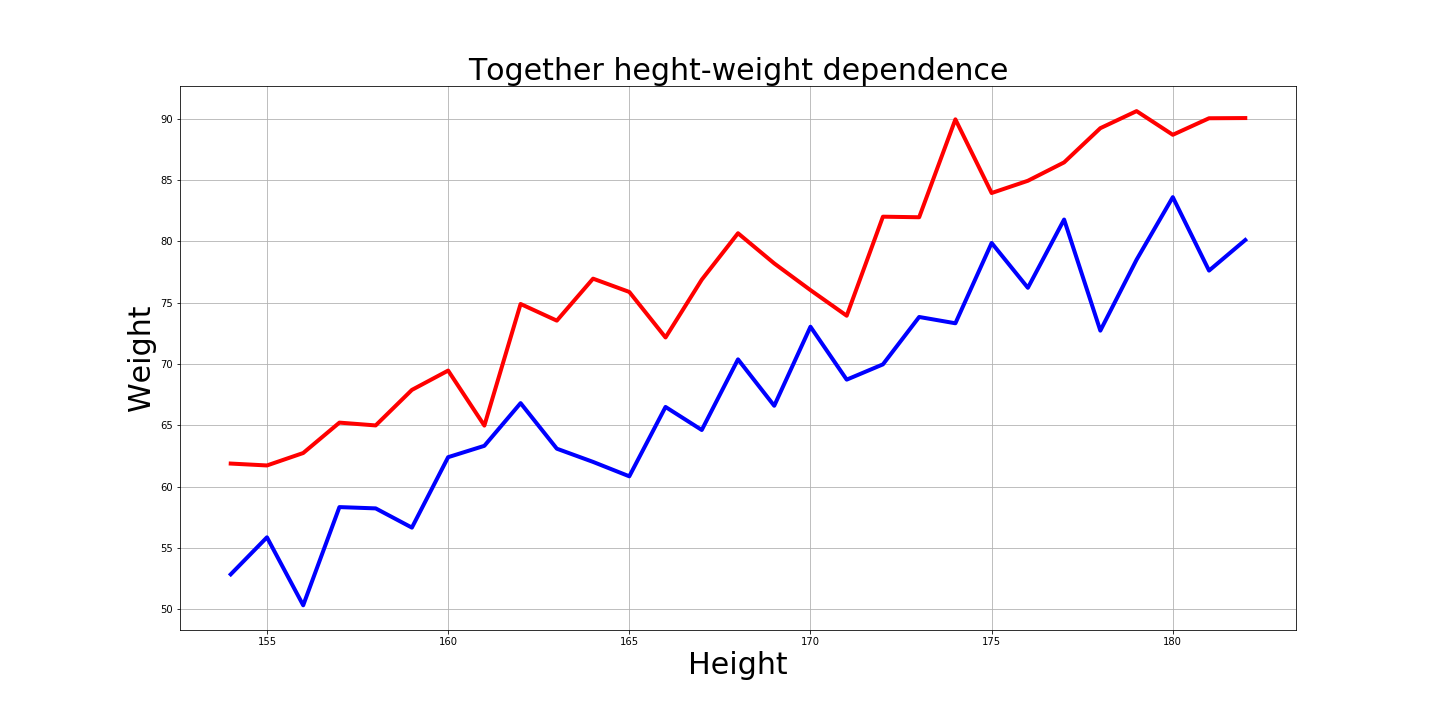
Respuestas a preguntas

- ¿Cuál es el rango de peso y altura para la mayoría de los hombres y mujeres?

99.7% de hombres: de 154cm a 197cm y de 58kg a 112kg.
Y el 99.7% de las mujeres: de 141cm a 182cm y de 36kg a 87kg.

- ¿Qué tipo de hombre "promedio" y mujer "promedio" son?

El hombre promedio mide 175 cm y 85 kg.
Y la mujer promedio mide 162 cm y 62 kg.

- ¿El modelo simple de aprendizaje automático KNN de estos datos predecirá peso por altura?

Sí, el modelo predijo 88 kg, y tengo 89,8 kg.

Todo lo que hice, lo recogí aquí

Contras del artículo

• No hay una descripción de DataSet. Probablemente, la edad y otros factores en las personas fueron diferentes. Por lo tanto, uno no puede aceptarlo por fe, sino por el bien del experimento, por favor.
• En el buen sentido, era necesario hacer una prueba de normalidad de distribución

Epílogo

Como si alcanzas el intervalo de 99.7%