ClickHouse encuentra constantemente tareas de procesamiento de cadenas. Por ejemplo, buscar, calcular las propiedades de cadenas UTF-8, o algo más exótico, ya sea una búsqueda que distingue entre mayúsculas y minúsculas o una búsqueda de datos comprimidos.
Todo comenzó con el hecho de que la gerente de desarrollo de ClickHouse, Lesha Milovidov o6CuFl2Q, vino a nosotros a la Facultad de Ciencias de la Computación de la Escuela Superior de Economía y ofreció una gran cantidad de temas para trabajos y diplomas. Cuando vi "Algoritmos de procesamiento de cadenas inteligentes en ClickHouse" (yo, una persona que está interesada en varios algoritmos, incluidos los experimentales), inmediatamente establecí planes sobre cómo hacer el mejor diploma. Mi alegría y expresión se pueden describir de la siguiente manera:

Clickhouse
ClickHouse pensó cuidadosamente en la organización del almacenamiento de datos en la memoria, en columnas. Al final de cada columna hay un relleno de 15 bytes para la lectura segura de un registro de 16 bytes. Por ejemplo, ColumnString almacena cadenas terminadas nulas junto con compensaciones. Es muy conveniente trabajar con tales matrices.

También hay ColumnFixedString, ColumnConst y LowCardinality, pero hoy no hablaremos de ellos con tanto detalle. El punto principal en este punto es que el diseño para la lectura segura de colas es simplemente hermoso, y la localidad de los datos también juega un papel en el procesamiento.
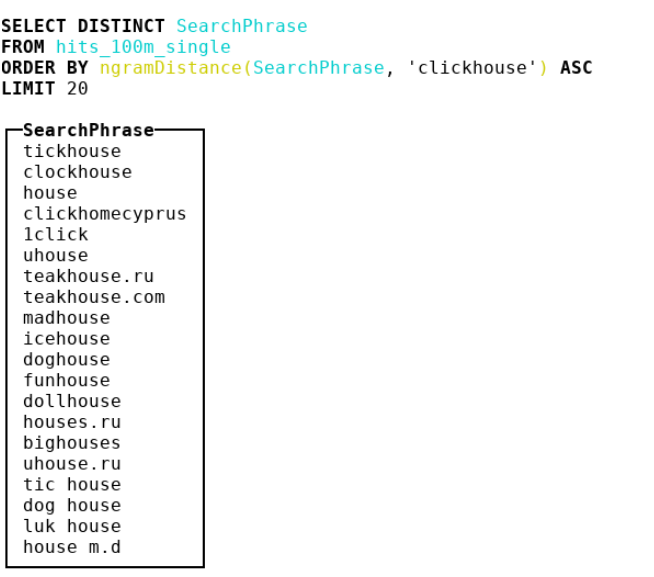
Búsqueda de subcadenas
Lo más probable es que conozca muchos algoritmos diferentes para encontrar una subcadena en una cadena. Hablaremos sobre los que se usan en ClickHouse. Primero presentamos un par de definiciones:
- pajar - la línea en la que estamos buscando; típicamente la longitud se denota por n .
- aguja - la cadena o expresión regular que estamos buscando; la longitud se denotará por m .
Después de estudiar una gran cantidad de algoritmos, puedo decir que hay 2 (máximo 3) tipos de algoritmos de búsqueda de subcadenas. El primero es la creación en una forma u otra de estructuras de sufijo. El segundo tipo son los algoritmos basados en la comparación de memoria. También está el algoritmo Rabin-Karp, que utiliza hashes, pero es bastante único en su tipo. El algoritmo más rápido no existe, todo depende del tamaño del alfabeto, la longitud de la aguja, el pajar y la frecuencia de ocurrencia.
Lea sobre diferentes algoritmos aquí . Y aquí están los algoritmos más populares:
- Knut - Morris - Pratt,
- Boyer - Moore,
- Boyer - Moore - Horspool,
- Rabin - Carpa,
- Doble cara (usado en glibc llamado "memmem"),
- BNDM
La lista continúa. En ClickHouse, honestamente lo intentamos todo, pero al final nos decidimos por una versión más extraordinaria.
Algoritmo de Volnitsky
El algoritmo fue publicado en el blog del programador Leonid Volnitsky a finales de 2010. Es algo que recuerda al algoritmo Boyer-Moore-Horspool, solo una versión mejorada.
Si m <4 , entonces se usa el algoritmo de búsqueda estándar. Guarde todas las agujas de bigrams (2 bytes consecutivos) desde el final en una tabla hash con direccionamiento abierto de tamaño | Sigma | 2 elementos (en la práctica, estos son 2 16 elementos), donde las compensaciones de este bigram serán los valores, y el bigram en sí mismo será el hash y el índice al mismo tiempo. La posición inicial estará en la posición m - 2 desde el comienzo del pajar. Seguimos al pajar con un paso de m - 1 , mira el siguiente bigram desde esta posición en el pajar y considera todos los valores del bigram en la tabla hash. Luego compararemos dos piezas de memoria con el algoritmo de comparación habitual. La cola que queda será procesada por el mismo algoritmo.
El paso m - 1 se elige de tal manera que si se produce una aguja en un pajar, definitivamente consideraremos el bigram de esta entrada, asegurando así que devolvamos la posición de la entrada en el pajar. La primera aparición está garantizada por el hecho de que agregamos índices desde el final a la tabla hash por bigram. Esto significa que cuando vamos de izquierda a derecha, primero consideraremos los bigrams desde el final de la línea (quizás inicialmente considerando bigrams completamente innecesarios), luego más cerca del comienzo.
Considera un ejemplo. Deje que el pajar de la cuerda sea abacabaac y la aguja igual a aaca . La tabla hash será {aa : 0, ac : 1, ca : 2} .
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Vemos el bigram ac . En aguja es, sustituimos en igualdad:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
No coincidió Después de ac no hay entradas en la tabla hash, pasamos al paso 3:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
No hay bigrams ba en la tabla hash, adelante:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Hay un bigram ca en aguja, miramos el desplazamiento y encontramos la entrada:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
El algoritmo tiene muchas ventajas. En primer lugar, no necesita asignar memoria en el montón, y 64 KB en la pila no son algo trascendental ahora. En segundo lugar, 2 16 es un número excelente para tomar un módulo para el procesador; estas son solo instrucciones movzwl (o, como bromeamos, "movsvl") y la familia.
En promedio, este algoritmo demostró ser el mejor. Tomamos los datos de Yandex.Metrica, las solicitudes son casi reales. Una velocidad de transmisión, más es mejor, KMP: algoritmo Knut - Morris - Pratt, BM: Boyer - Moore, BMH: Boyer - Moore - Horspool.
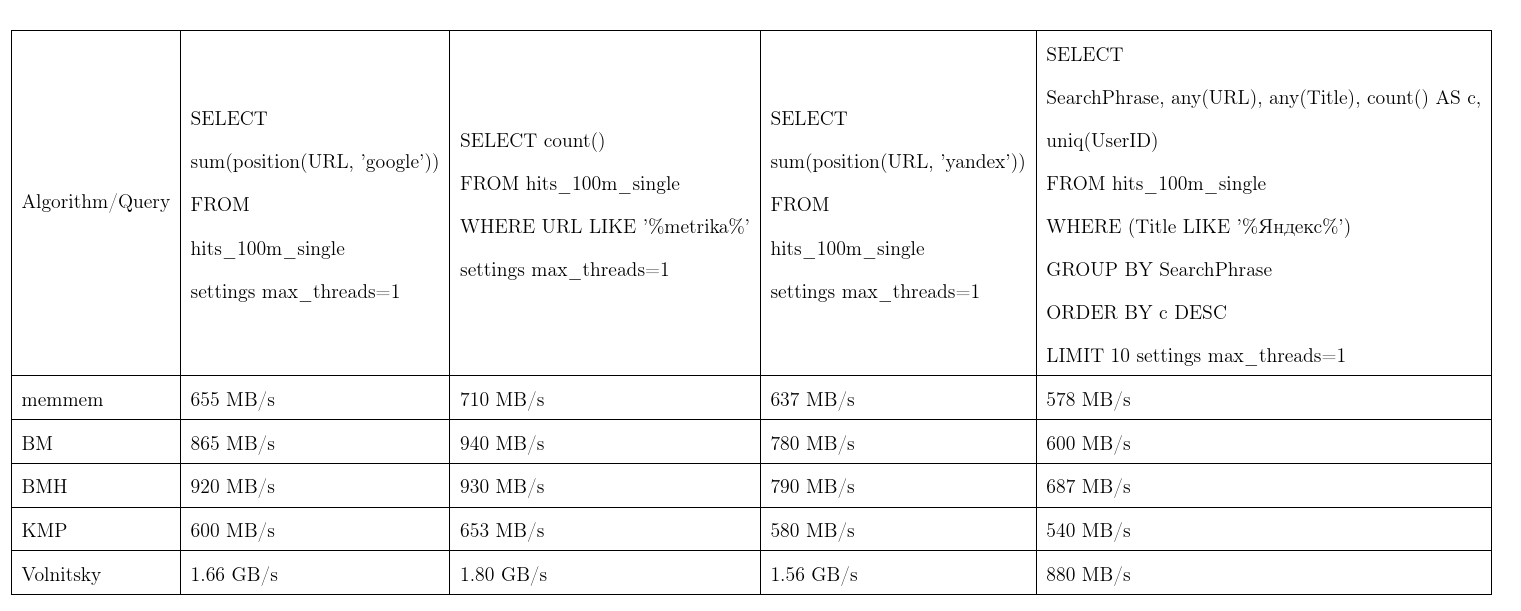
Para no ser infundado, el algoritmo puede funcionar en tiempo cuadrático:

Se utiliza en la función de position(Column, ConstNeedle) y también actúa como una optimización para búsquedas de expresiones regulares.
Búsqueda de expresiones regulares
Le diremos cómo ClickHouse optimiza las búsquedas de expresiones regulares. Muchas expresiones regulares contienen una subcadena dentro, que debe estar dentro de un pajar. Para no construir una máquina de estados finitos y verificarla, aislaremos tales subcadenas.
Hacer esto es bastante simple: cualquier paréntesis de apertura aumenta el nivel de anidación, cualquier paréntesis de cierre disminuye; También hay caracteres específicos para las expresiones regulares (por ejemplo, '.', '*', '?', '\ w', etc.). Necesitamos obtener todas las subcadenas en el nivel 0. Considere un ejemplo:
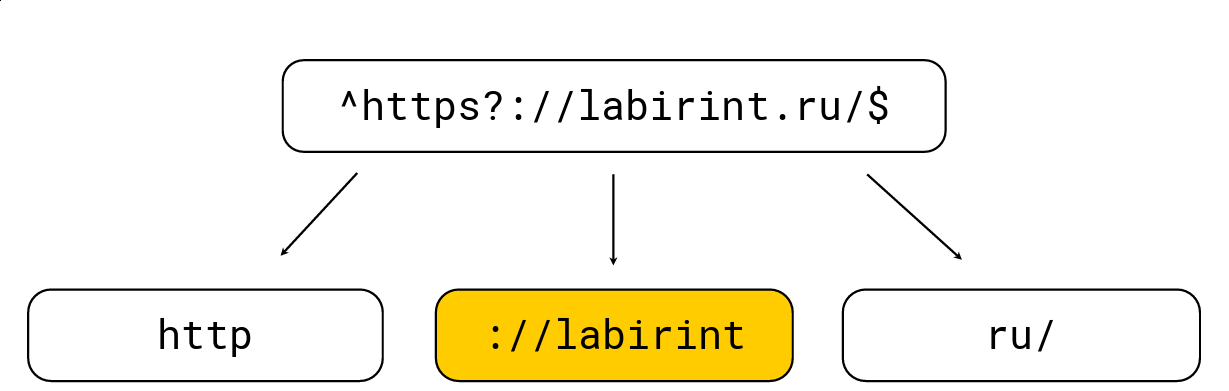
Lo dividimos en esas subcadenas que deben estar en el pajar de la expresión regular, después de lo cual seleccionamos la longitud máxima, buscamos candidatos en él y luego verificamos con el motor de expresión regular RE2 habitual. Hay una expresión regular en la imagen de arriba, es procesada por el motor RE2 habitual a 736 MB / s, Hyperscan (aproximadamente un poco más tarde) maneja a 1.6 GB / s, y manejamos 1.69 GB / s por núcleo, junto con la descompresión LZ4. En general, dicha optimización está en la superficie y acelera en gran medida la búsqueda de expresiones regulares, pero a menudo no se implementa en herramientas, lo que me sorprende mucho.
La palabra clave LIKE también se optimiza utilizando este algoritmo, solo después de LIKE puede aparecer una expresión regular muy simplificada en %%%%%% (subcadena arbitraria) y _ (carácter arbitrario).
Desafortunadamente, no todas las expresiones regulares están sujetas a tales optimizaciones, por ejemplo, desde yandex|google es imposible extraer explícitamente las subcadenas que deben ocurrir en el pajar. Por lo tanto, se nos ocurrió una solución completamente diferente.
Busca muchas subcadenas
El problema es que hay muchas agujas, y quiero entender si al menos una de ellas está incluida en el pajar. Existen métodos bastante clásicos para tal búsqueda, por ejemplo, el algoritmo Aho-Korasik. Pero no fue demasiado rápido para nuestra tarea. Hablaremos de esto un poco más tarde.
Lesha ClickHouse adora las soluciones no estándar, por lo que decidimos probar algo diferente y, tal vez, crear un nuevo algoritmo de búsqueda. Y lo hicieron.
Observamos el algoritmo Volnitsky y lo modificamos para que comenzara a buscar muchas subcadenas a la vez. Para hacer esto, solo necesita agregar los bigrams de todas las filas y almacenar además un índice de fila en la tabla hash. El paso se seleccionará de al menos todas las longitudes de aguja menos 1 para garantizar nuevamente la propiedad de que si ocurre, veremos su bigram. La tabla hash crecerá a 128 KB (las líneas más largas que 255 son procesadas por el algoritmo estándar, consideraremos no más de 256 agujas). Soy muy vago, así que aquí hay un ejemplo de la presentación (leída de izquierda a derecha de arriba a abajo):


Comenzamos a ver cómo se comporta tal algoritmo en comparación con otros (las filas se toman de datos reales). Y para un pequeño número de líneas, hace todo (se indica la velocidad junto con la descarga, aproximadamente 2.5 GB / s).
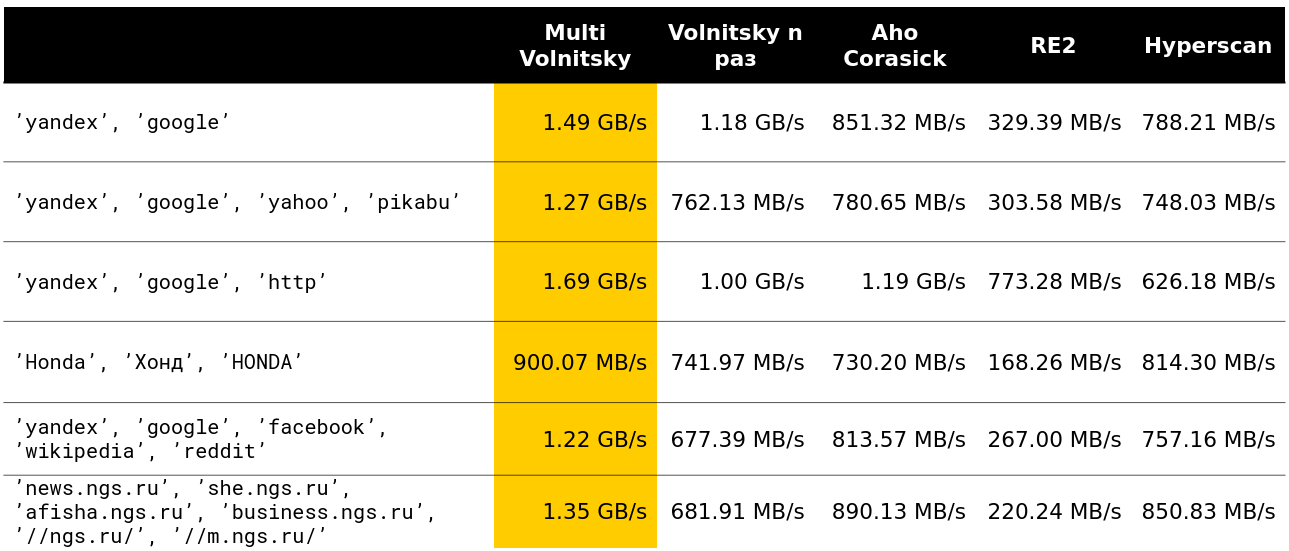
Entonces se hizo interesante. Por ejemplo, con una gran cantidad de bigrams similares, perdemos ante algunos competidores. Es comprensible: comenzamos a comparar muchos recuerdos y a degradarnos.

No puede acelerar mucho si la longitud mínima de la aguja es lo suficientemente grande. Obviamente, tenemos más oportunidades para omitir piezas enteras de pajar sin pagar nada por ello.

El punto de inflexión comienza en algún lugar de las líneas 13-15. Alrededor del 97% de las solicitudes que vi en el clúster eran menos de 15 filas:
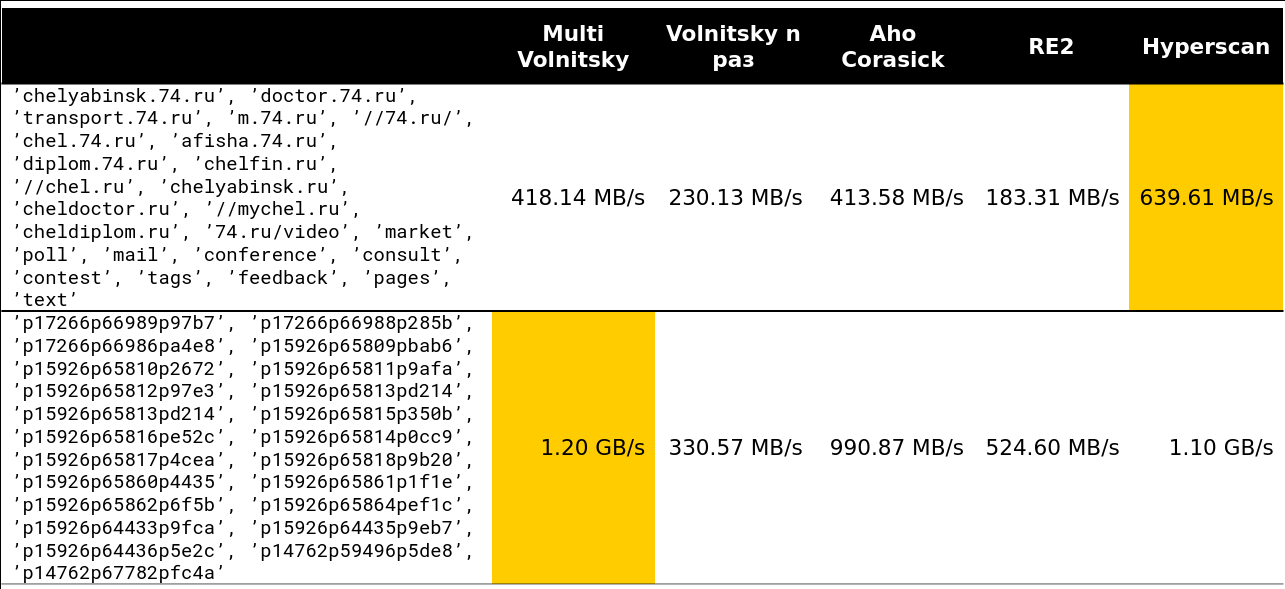
Bueno, una imagen muy aterradora: 41 líneas, muchas bigrams repetidas:

Como resultado, en ClickHouse (19.5) implementamos las siguientes funciones a través de este algoritmo:
- multiSearchAny(h, [n_1, ..., n_k]) - 1, si al menos una de las agujas está en el pajar.
- multiSearchFirstPosition(h, [n_1, ..., n_k]) : la posición de entrada más a la izquierda en el pajar (de uno) o 0 si no se encuentra.
- multiSearchFirstIndex(h, [n_1, ..., n_k]) : el índice de la aguja más a la izquierda, que se encontró en el pajar; 0 si no se encuentra.
- multiSearchAllPositions(h, [n_1, ..., n_k]) : todas las primeras posiciones de todas las agujas devuelven una matriz.
Los sufijos son -UTF8 (no normalizamos), -CaseInsensitive (agregue 4 bigrams con mayúsculas y minúsculas diferentes), -CaseInsensitiveUTF8 (existe la condición de que las letras mayúsculas y minúsculas deben tener el mismo número de bytes). Vea la implementación aquí .
Después de eso, nos preguntamos si podríamos hacer algo similar con muchas expresiones regulares. Y encontraron una solución que ya estaba estropeada en los puntos de referencia.
Buscar por muchas expresiones regulares
Hyperscan es una biblioteca de Intel que busca de inmediato muchas expresiones regulares. Utiliza la heurística para aislar las subpalabras de las expresiones regulares sobre las que escribimos, y muchos SIMD para buscar el autómata Glushkov (el algoritmo parece llamarse Teddy).
En general, todo está en las mejores tradiciones de sacar el máximo provecho de la búsqueda de expresiones regulares. La biblioteca realmente hace lo que se declara en sus funciones.

Afortunadamente, en mi mes de desarrollo en ClickHouse, pude superar el desarrollo de 12 años en una clase de consultas decente y estoy muy satisfecho con esto.
En Yandex, la biblioteca Hyperscan también se usa en antispam. A juzgar por las revisiones, procesa con calma miles de expresiones regulares y las busca rápidamente.
La biblioteca tiene varias desventajas. El primero es la cantidad indocumentada de memoria consumida y una característica extraña de que el pajar debe tener menos de 2 32 bytes. El segundo: no puede devolver las primeras posiciones de forma gratuita, los índices de aguja más a la izquierda, etc. Y el tercer signo negativo: hay algunos errores de la nada. Por lo tanto, en ClickHouse, implementamos las siguientes funciones usando Hyperscan:
- multiMatchAny(h, [n_1, ..., n_k]) - 1, si al menos una de las agujas tiene pajar.
- multiMatchAnyIndex(h, [n_1, ..., n_k]) : cualquier índice de la aguja que multiMatchAnyIndex(h, [n_1, ..., n_k]) pajar.
Estamos interesados, pero ¿cómo puede buscar no exactamente, sino aproximadamente? Y se le ocurrieron varias soluciones.
Búsqueda aproximada
El estándar en la búsqueda aproximada es la distancia de Levenshtein: el número mínimo de caracteres que se pueden reemplazar, agregar y eliminar para obtener una cadena b de longitud n de una cadena a de longitud m. Desafortunadamente, el ingenuo algoritmo de programación dinámica funciona para O (mn) ; las mejores mentes de ShAD pueden hacerlo en O (mn / log max (n, m)) ; es fácil pensar en O ((n + m) ⋅ alfa) , donde alfa es la respuesta; la ciencia puede hacerlo para O ((alpha - | n - m |) min (m, n, alpha) + m + n) (el algoritmo es simple, leer al menos en el ShAD) o, si es un poco más claro, para O (alpha ^ 2 + m + n) . Todavía hay un punto negativo: lo más probable es que sea imposible deshacerse del tiempo cuadrático en el peor de los casos polinomialmente. Peter Indik escribió un artículo muy poderoso sobre esto.
Hay un ejercicio: imagine que por reemplazar un personaje en la distancia de Levenshtein paga una multa, no dos, sino dos; luego, encuentre un algoritmo para O ((n + m) log (n + m)) .
Todavía no funciona, demasiado largo y costoso. Pero con la ayuda de tal distancia, hicimos la detección de errores tipográficos en las consultas.
Además de la distancia de Levenshtein, hay una distancia de Hamming. Con él también, todo es bastante malo, pero un poco mejor que con la distancia de Levenshtein. No tiene en cuenta la eliminación de caracteres, pero considera solo para dos líneas de la misma longitud el número de caracteres en los que difieren. Por lo tanto, si usamos la distancia para cadenas de longitud m <n, entonces solo en la búsqueda de las subcadenas más cercanas.
Cómo calcular dicha matriz de discrepancias (una matriz d de n - m + 1 elementos, donde d [i] es el número de caracteres diferentes en el i-ésimo desde el comienzo de la superposición) para O (| Sigma | (n + m) log (n + m) ) ? Primero, haz | Sigma | Máscaras de bits que indican si este símbolo es igual al considerado. A continuación, calculamos la respuesta para cada una de las máscaras Sigma y sumamos: obtenemos la respuesta original.
Considera un ejemplo. abba , subcadena ba , alfabeto binario. Obtenemos 2 máscaras 1001, 01 y 0110, 10 .
a 1001 01 - 0 01 - 0 01 - 1
b 0110 10 - 0 10 - 1 10 - 1
Obtenemos la matriz [0, 1, 2], esta es casi la respuesta correcta. Pero tenga en cuenta que para cada letra, el número de coincidencias es solo el producto escalar de una aguja binaria fija y todas las subcadenas de pajar. Y para esto, por supuesto, ¡hay una rápida transformación de Fourier!
Para aquellos que no saben: la FFT puede multiplicar dos polinomios de grados m <n en un tiempo O (n log n) , siempre que el trabajo con los coeficientes se realice por unidad de tiempo. Las convoluciones son muy similares a los productos escalares. Es suficiente duplicar los coeficientes del primer polinomio, y expandir y complementar el segundo con el número requerido de ceros, luego obtenemos todos los productos escalares de una cadena binaria y todas las subcadenas de la otra en O (n log n) , ¡algún tipo de magia! Pero créeme, esto es absolutamente real, y a veces la gente lo hace.
Pero no en ClickHouse. Para nosotros, trabajando con | Sigma | = 30 ya es grande, y el FFT no es el algoritmo práctico más agradable para el procesador o, como dicen en la gente común, "la constante es grande".
Por lo tanto, decidimos mirar otras métricas. Llegamos a la bioinformática, donde las personas usan la distancia de n gramos. De hecho, tomamos todos los n-gramos de pajar y aguja, consideremos 2 multisets con estos n-gramos. Luego tomamos la diferencia simétrica y la dividimos por la suma de las cardinalidades de dos conjuntos múltiples con n-gramos. Obtenemos un número del 0 al 1: cuanto más cerca de 0, más se parecen las líneas. Considere un ejemplo donde n = 4 :
abcda → {abcd, bcda}; Size = 2 bcdab → {bcda, cdab}; Size = 2 . |{abcd, cdab}| / (2 + 2) = 0.5
Como resultado, hicimos una distancia de 4 gramos y atascamos un montón de ideas de SSE allí, y también debilitamos ligeramente la implementación a hash crc32 de doble byte.
Echa un vistazo a la implementación . Precaución: código muy convincente y optimizado para compiladores.
Le aconsejo especialmente que preste atención al truco sucio para emitir minúsculas para los puntos de código ASCII y ruso.
- ngramDistance(haystack, needle) : devuelve un número de 0 a 1; cuanto más cerca de 0, más líneas son similares entre sí.
- -UTF8, -CaseInsensitive, -CaseInsensitiveUTF8 (truco sucio para rusos y ASCII).
Hyperscan tampoco se detiene; tiene la funcionalidad de búsqueda aproximada: puede buscar líneas que parecen expresiones regulares por la distancia constante de Levenshtein. Se crea un autómata distancia + 1 , que se interconecta eliminando, reemplazando o insertando un carácter, que significa "bien", después de lo cual se aplica el algoritmo habitual para verificar si un autómata acepta una línea en particular. En ClickHouse, los implementamos con los siguientes nombres:
- multiFuzzyMatchAny(haystack, distance, [n_1, ..., n_k]) - similar a multiMatchAny, solo con distancia.
- multiFuzzyMatchAnyIndex(haystack, distance, [n_1, ..., n_k]) - similar a multiMatchAnyIndex, solo con distancia.
Con el aumento de la distancia, la velocidad comienza a degradarse mucho, pero aún se mantiene en un nivel bastante decente.
Finalice la búsqueda y comience a procesar cadenas UTF-8. También hubo muchas cosas interesantes.
Procesamiento de línea UTF-8
Admito que fue difícil romper el techo de implementaciones ingenuas en cadenas codificadas UTF-8. Fue especialmente difícil atornillar SIMD. Compartiré algunas ideas sobre cómo hacer esto.
Recuerde cómo se ve una secuencia UTF-8 válida:
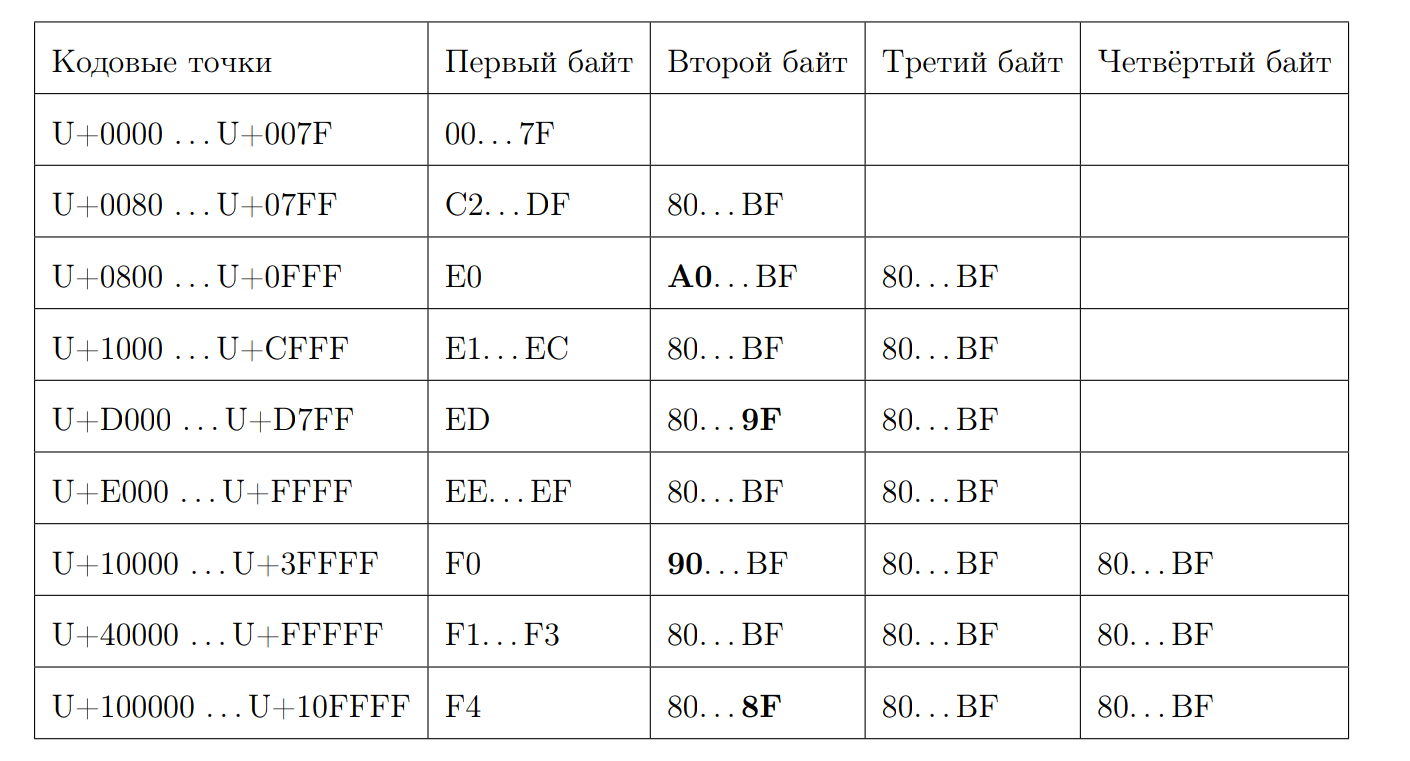
Intentemos calcular la longitud del punto de código por el primer byte. Aquí es donde comienza la magia de bits. Nuevamente escribimos algunas propiedades:
- Comenzando en 0xC y en 0xD tienen 2 bytes
- 0xC2 = 11 0 00010
- 0xDF = 11 0 11111
- 0xE0 = 111 0 0000
- 0xF4 = 1111 0 100, no hay nada más que 0xF4, pero si hubiera 0xF8, habría una historia diferente
- Responda 7 menos la posición del primer cero desde el final, si no es un carácter ASCII
Calculamos la longitud:
inline size_t seqLength(const UInt8 first_octet) { if (first_octet < 0x80u) return 1; const auto first_zero = bitScanReverse(static_cast<UInt8>(~first_octet)); return 7 - first_zero; }
Afortunadamente, tenemos en stock instrucciones que pueden calcular el número de bits cero, comenzando por los más significativos.
f = __builtin_clz(val)
Calcular bitScanReverse:
unsigned int bitScanReverse(unsigned int x) { return 31 - __builtin_clz(x); }
Intentemos calcular la longitud de una cadena UTF-8 por puntos de código a través de SIMD. Para hacer esto, mire cada byte como un número con signo y observe las siguientes propiedades:
- 0xBF = -65
- 0x80 = -128
- 0xC2 = -62
- 0x7F = 127
- todos los primeros bytes están en [0xC2, 0x7F]
- todos los primeros bytes están en [0x80, 0xBF]
El algoritmo es bastante simple. Compare cada byte con -65 y, si es mayor que este número, agregue uno. Si queremos usar SIMD, entonces esta es la carga habitual de 16 bytes del flujo de entrada. Luego hay una comparación de bytes, que en el caso de un resultado positivo dará el byte 0xFF, y en el caso de un negativo - 0x00. Luego, la instrucción pmovmskb , que recopilará los bits altos de cada byte del registro. Luego, el número de guiones bajos aumenta, usamos el intrínseco para la instrucción popcnt SSE4. El esquema de este algoritmo puede ilustrarse con un ejemplo:

Resulta que, junto con la descompresión, el procesamiento por núcleo será de aproximadamente 1,5 GB / s.
Las funciones se llaman:
- lengthUTF8(string) : devuelve la longitud de una cadena UTF-8 codificada correctamente, se considera que algo no es válido, no se produce una excepción.
Fuimos más allá porque queríamos aún más funciones con el procesamiento de cadenas UTF-8. Por ejemplo, verificar la validez y convertir a una expresión UTF-8 válida.
Para verificar la validez, tomé https://github.com/cyb70289/utf8/ , adaptado para ClickHouse (en realidad solo cambié el procesamiento de las colas) y obtuve una velocidad de 1.22 GB / s en comparación con 900 MB / s para el algoritmo ingenuo . No describiré el algoritmo en sí, es bastante complicado para la percepción.
- isValidUTF8(string) : devuelve 1 si la cadena está codificada correctamente con UTF-8; de lo contrario, 0.
- toValidUTF8(string) : reemplaza los caracteres UTF-8 no válidos con el carácter (U + FFFD). Todos los caracteres inválidos consecutivos colapsan en un carácter de reemplazo. No hay ciencia espacial.
En general, en las líneas UTF-8, debido al esquema estático no tan agradable, siempre es difícil encontrar algo que esté bien optimizado.
Que sigue
Déjame recordarte que esta fue mi tesis. Por supuesto, la defendí por 10/10. Ya fuimos con ella a Highload ++ Siberia (aunque me pareció que no le interesaba a nadie). Mira la presentación . Me gustó que la parte práctica de la tesis resultó en una gran cantidad de investigaciones interesantes. Y aquí está el diploma en sí. Tiene muchos errores tipográficos, porque nadie lo leyó. :)
Como parte de la preparación del diploma, hice un montón de otros trabajos similares (los enlaces conducen a solicitudes de grupo):
- Función optimizada de concat 2 veces ;
- Hizo el formato de Python más simple para solicitudes ;
- Acelerado LZ4 en un 4% ;
- Hice un gran trabajo en SIMD para ARM y PPC64LE ;
- Y aconsejó a un par de estudiantes del FCS con diplomas en ClickHouse.
Al final, resultó que, en mi experiencia, cada mes Lesha intentaba cantarme ClickHouse es el sistema más agradable para escribir código de alto rendimiento, donde hay documentación, comentarios, excelente soporte para desarrolladores y desarrolladores. ClickHouse es impresionante, de verdad. ¿Cansado de cambiar los formatos JSON? Venga a Lesha y solicite una tarea de cualquier nivel: él se la proporcionará y durante el fin de semana obtendrá un gran placer escribiendo código.
Pero con todos los logros de ClickHouse y su diseño, probablemente no se trata de ellos. No principalmente en ellos.
Pasé 4 años de estudios de pregrado en el FCS, en junio me gradué del HSE con honores, trabajé durante un año y medio en un equipo increíble en Yandex, después de haber bombeado bien. Sin experiencia total todo este tiempo y hierro Nada de lo escrito en la publicación hubiera funcionado. FCN es muy bueno, si le quitas el máximo. Gracias a Vana Puzyrevsky ivan_puzyrevskiy , Ignat Kolesnichenko, Gleb Evstropov, Max Babenko maxim_babenko por reunirse en mi divertida aventura en FCN. Y también gracias a todos los profesores que me enseñaron algo.