"Si lees la inscripción" búfalo "en la jaula del elefante, no le creas a tus ojos" Kozma Prutkov

En un artículo anterior sobre diseño orientado a modelos , se demostró por qué se necesita un modelo de objetos, y se demostró que sin este modelo de objetos, el diseño basado en modelos solo puede considerarse una tormenta de marketing, sin sentido y despiadado. Pero cuando aparece un modelo de objeto, los ingenieros competentes siempre tienen una pregunta razonable: qué evidencia hay de que el modelo matemático de un objeto corresponde a un objeto real.

Un ejemplo de respuesta a esta pregunta se da en un artículo sobre diseño orientado a modelos de un motor eléctrico. En este artículo, consideraremos un ejemplo de creación de un modelo para sistemas de aire acondicionado de aviación, diluyendo la práctica con algunas consideraciones teóricas generales.

Crear un modelo confiable del objeto. Teoría

Para no tirar de la goma, te contaré de inmediato sobre el algoritmo para crear un modelo para un diseño orientado al modelo. Tiene solo tres pasos simples:

Paso 1. Desarrolle un sistema de ecuaciones algebraicas-diferenciales que describan el comportamiento dinámico de los sistemas simulados. Es simple si conoce la física del proceso. Muchos científicos ya han desarrollado para nosotros las leyes físicas básicas del nombre de Newton, Brenuli, Navier Stokes y otros Shtangels of Compasses y Rabinovich.

Paso 2. En el sistema resultante, aísle el conjunto de coeficientes empíricos y características del objeto de simulación que se pueden obtener de las pruebas.

Paso 3. Realice pruebas del objeto y ajuste el modelo de acuerdo con los resultados de los experimentos de campo, de modo que corresponda a la realidad, con el grado de detalle necesario.

Como puede ver, solo dos tres.

Ejemplo práctico

El sistema de aire acondicionado (SCR) en la aeronave está conectado al sistema automático de mantenimiento de presión. La presión en la aeronave siempre debe ser mayor que la presión externa, mientras que la tasa de cambio de presión debe ser tal que los pilotos y los pasajeros no sangran nariz y oídos. Por lo tanto, el sistema de control de la entrada y salida de aire es importante para la seguridad, y se ponen en marcha costosos sistemas de prueba para su desarrollo. Crean temperaturas y presiones de altitud de vuelo, reproducen modos de despegue y aterrizaje en aeródromos de diferentes alturas. Y la cuestión de desarrollar y depurar sistemas de control de divisas está aumentando a su máximo potencial. ¿Cuánto tiempo manejaremos el banco de pruebas para obtener un sistema de control satisfactorio? Obviamente, si ajustamos el modelo de control al modelo de objeto, el ciclo de trabajo en el banco de pruebas puede reducirse significativamente.

El sistema de aire acondicionado de aviación consta de los mismos intercambiadores de calor que cualquier otro sistema térmico. Batería: también es una batería en África, solo aire acondicionado. Pero debido a la limitación de la masa de despegue y las dimensiones de la aeronave, los intercambiadores de calor se hacen lo más compactos y lo más eficientes posible para transferir la mayor cantidad de calor posible desde la masa más baja. Como resultado, la geometría se vuelve bastante extraña. Como por ejemplo en el caso bajo consideración. La Figura 1 muestra un intercambiador de calor de placas, en el que se usa una membrana entre las placas para mejorar la transferencia de calor. El refrigerante caliente y el frío se alternan en los canales, mientras que la dirección del flujo es transversal. Se suministra un refrigerante al corte frontal y el otro al lateral.

Para resolver el problema de control de SCR, necesitamos saber cuánto calor se transfiere de un medio a otro en dicho intercambiador de calor por unidad de tiempo. La tasa de cambio de temperatura depende de esto, que regulamos.

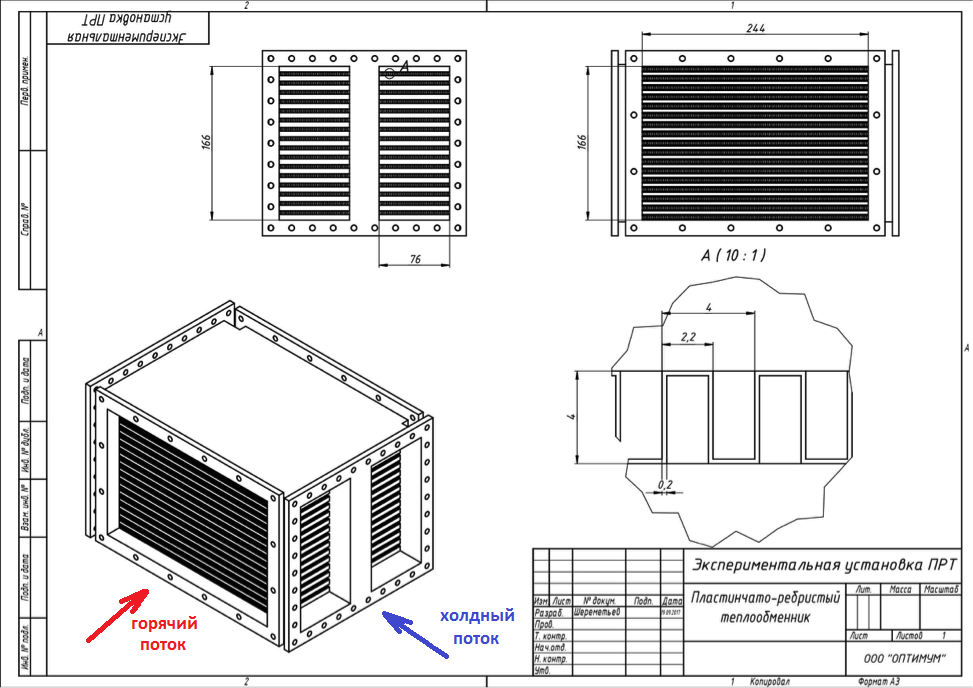
Figura 1. Diagrama del intercambiador de calor de la aeronave.

Problemas de modelado. Parte hidraulica

A primera vista, la tarea es bastante simple, es necesario calcular el flujo másico a través de los canales del intercambiador de calor y el flujo de calor entre los canales.
El caudal másico del refrigerante en los canales se calcula utilizando la fórmula de Bernoulli:

donde:
ΔP es la caída de presión entre dos puntos;
ξ es el coeficiente de fricción del refrigerante;
L es la longitud del canal;
d es el diámetro hidráulico del canal;
ρ es la densidad del refrigerante;
ω es la velocidad del refrigerante en el canal.

Para un canal de forma arbitraria, el diámetro hidráulico se calcula mediante la fórmula:

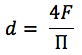
donde:
F es el área del agujero;
P - perímetro del canal mojado.

El coeficiente de fricción se calcula de acuerdo con fórmulas empíricas y depende de la velocidad del flujo y de las propiedades del refrigerante. Para diferentes geometrías, se obtienen diferentes dependencias, por ejemplo, la fórmula para el flujo turbulento en tuberías lisas:

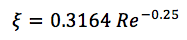
donde:
Re es el número de Reynolds.

Para el flujo en canales planos, se puede usar la siguiente fórmula:

A partir de la fórmula de Bernoulli, puede calcular la caída de presión para una velocidad determinada, o viceversa, calcular la velocidad del refrigerante en el canal, en función de una caída de presión dada.

Transferencia de calor

El flujo de calor entre el refrigerante y la pared se calcula mediante la fórmula:

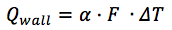
donde:
α [W / (m2 × deg)] - coeficiente de transferencia de calor;
F es el área del agujero.

Para problemas de flujo de refrigerantes en tuberías, se ha realizado un número suficiente de estudios y hay muchos métodos de cálculo, y como regla general, todo se reduce a dependencias empíricas, para el coeficiente de transferencia de calor α [W / (m2 × deg)]

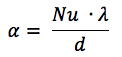
donde:
Nu es el número de Nusselt,
λ es la conductividad térmica del líquido [W / (m × deg)]
d es el diámetro hidráulico (equivalente).

Las dependencias de criterios empíricos se utilizan para calcular el número de Nusselt (criterio), por ejemplo, la fórmula para calcular el número de Nusselt de una tubería redonda se ve así:

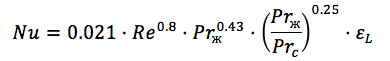
Aquí ya vemos el número de Reynolods, el número de Prandtl a la temperatura de la pared y la temperatura del fluido, y el coeficiente de desigualdad. ( Fuente )

Para los intercambiadores de calor de placas corrugadas, la fórmula es similar ( Fuente ):

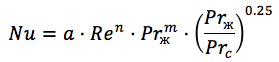
donde:
n = 0.73 m = 0.43 para un flujo turbulento,
coeficiente a - varía entre 0.065 y 0.6 dependiendo del número de placas y el régimen de flujo.

Tenga en cuenta que este coeficiente se calcula para un solo punto en la secuencia. Para el siguiente punto, tenemos una temperatura de líquido diferente (se ha calentado o enfriado), una temperatura de pared diferente y, en consecuencia, todos los números de Reynolds y Prandtl están flotando.

En este punto, cualquier matemático dirá que es imposible calcular exactamente el sistema en el que el coeficiente cambia 10 veces, y tendrá razón.

Cualquier ingeniero en ejercicio dirá que cada intercambiador de calor es diferente en la fabricación y que es imposible calcular los sistemas, y también será correcto.

Pero, ¿qué pasa con el diseño orientado a modelos? ¿Se ha ido todo?

Los vendedores avanzados de software occidental en este lugar lo emparejarán con un Supercomputador y sistemas de cálculo 3D, como "sin él de ninguna manera". Y debe ejecutar el cálculo durante un día para obtener la distribución de temperatura durante 1 minuto.

Está claro que esta no es nuestra opción, debemos depurar el sistema de control, si no en tiempo real, al menos en el futuro previsible.

Método de empuje

Se fabrica un intercambiador de calor, se llevan a cabo una serie de pruebas y se establece una tabla de la eficiencia de la temperatura de estado estable a los caudales dados. Simple, rápido y confiable, como los datos obtenidos de las pruebas.

La desventaja de este enfoque es que no hay características dinámicas del objeto. Sí, sabemos cuál será el flujo de calor en estado estable, pero no sabemos cuánto tiempo se establecerá al cambiar de un modo de operación a otro.

Por lo tanto, después de calcular las características necesarias, configuramos el sistema de control directamente durante las pruebas, lo que nos gustaría evitar desde el principio.

Enfoque orientado al modelo

Para crear un modelo de intercambiador de calor dinámico, es necesario utilizar datos de prueba para eliminar las incertidumbres en las fórmulas de cálculo empírico: el número de Nusselt y la resistencia hidráulica.

La decisión es simple, como todo ingenioso. Tomamos la fórmula empírica, realizamos experimentos y determinamos el valor del coeficiente a, eliminando así la incertidumbre en la fórmula.

Tan pronto como tengamos un cierto valor del coeficiente de transferencia de calor, todos los demás parámetros están determinados por las leyes físicas básicas de conservación. La diferencia de temperatura y el coeficiente de transferencia de calor determinan la cantidad de energía transferida al canal por unidad de tiempo.

Conociendo el flujo de energía, es posible resolver las ecuaciones de conservación de la masa de energía y el momento para el refrigerante en el canal hidráulico. Por ejemplo, esto:

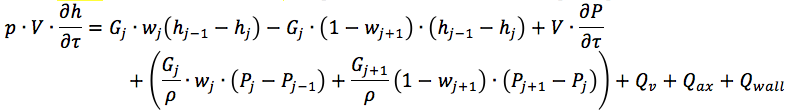
Para nuestro caso, el flujo de calor entre la pared y el refrigerante, Qwall, permanece indeterminado. Más detalles se pueden encontrar aquí ...

Y también la ecuación para la derivada de temperatura para la pared del canal:

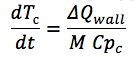
donde:
ΔQ _pared - la diferencia entre el flujo entrante y saliente a la pared del canal;
M es la masa de la pared del canal;
C _pc es la capacidad calorífica del material de la pared.

Precisión del modelo

Como se mencionó anteriormente, en el intercambiador de calor tenemos una distribución de temperatura sobre la superficie de la placa. Para el valor de estado estacionario, se puede tomar el promedio sobre las placas y usarlo, presentando todo el intercambiador de calor como un único punto concentrado, en el cual la transferencia de calor ocurre sobre toda la superficie del intercambiador de calor con la misma diferencia de temperatura. Pero para los modos transitorios, esta aproximación puede no funcionar. El otro extremo es hacer varios cientos de miles de puntos y cargar el Super Computer, que tampoco nos conviene, ya que la tarea es configurar el sistema de control en tiempo real, o mejor, más rápido.

Surge la pregunta: ¿cuántas secciones necesita para romper el intercambiador de calor para obtener una precisión y velocidad de cálculo aceptables?

Como siempre por casualidad, tenía a mano un modelo de intercambiador de calor de amina. El intercambiador de calor es un tubo, el medio calefactor fluye por las tuberías y se calienta entre las fosas. Para simplificar la tarea, todo el tubo del intercambiador de calor se puede representar como una tubería equivalente, y la tubería en sí se puede representar como un conjunto de celdas de cálculo discretas, en cada una de las cuales se calcula un modelo de transferencia de calor. El diagrama modelo de una sola celda se muestra en la Figura 2. El canal de aire caliente y el canal de aire frío están conectados a través de una pared que proporciona transferencia de calor entre los canales.

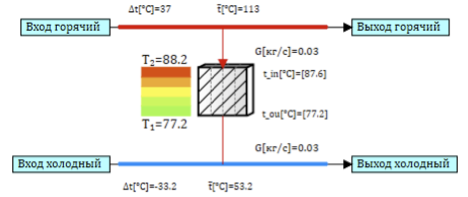
Figura 2. Modelo de celda del intercambiador de calor.

El modelo de intercambiador de calor tubular es fácilmente personalizable. Puede cambiar solo un parámetro: el número de secciones a lo largo de la tubería y ver los resultados de cálculo para diferentes particiones. Calcularemos varias opciones, comenzando por dividir en 5 puntos de longitud (Fig. 3) y hasta 100 puntos de longitud (Fig. 4).

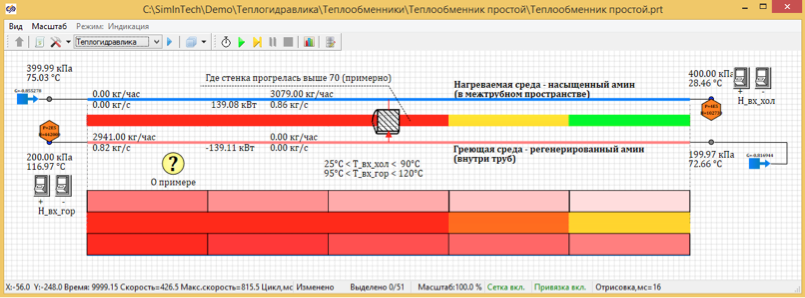
Figura 3. Distribución de temperatura estacionaria de 5 puntos de diseño.

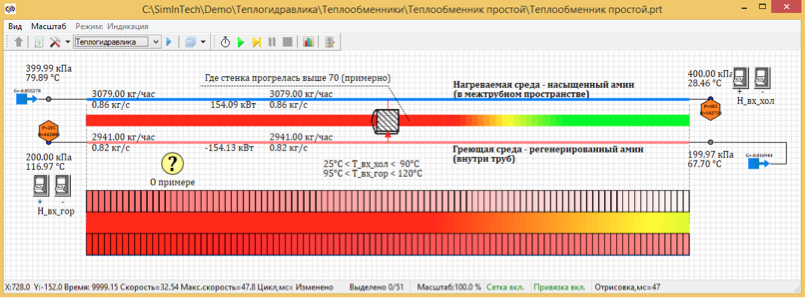
Figura 4. Distribución de temperatura estacionaria de 100 puntos de diseño.

Como resultado de los cálculos, resultó que la temperatura en estado estacionario cuando se divide por 100 puntos es de 67.7 grados. Y cuando se divide en 5 puntos calculados, la temperatura es 72, 66 grados C.

Además, la velocidad de cálculo relativa al tiempo real se muestra en la parte inferior de la ventana.
Veamos cómo cambian la temperatura de estado estable y la velocidad de cálculo según el número de puntos de diseño. La diferencia en las temperaturas de estado estacionario en los cálculos con un número diferente de celdas de cálculo se puede utilizar para evaluar la precisión del resultado.

Tabla 1. La dependencia de la temperatura y la velocidad de cálculo del número de puntos de diseño a lo largo de la longitud del intercambiador de calor.

Analizando esta tabla, podemos sacar las siguientes conclusiones:

• La velocidad de cálculo disminuye en proporción al número de puntos de diseño en el modelo de intercambiador de calor.
• El cambio en la precisión del cálculo ocurre exponencialmente. A medida que aumenta el número de puntos, disminuye el refinamiento en cada aumento posterior.

En el caso de un intercambiador de calor de placas con un portador de calor de flujo cruzado, como en la Figura 1, la creación de un modelo equivalente a partir de celdas de diseño elementales es un poco complicado. Necesitamos conectar las células de tal manera que organicemos el flujo cruzado. Para 4 celdas, el circuito se verá como se muestra en la Figura 5.

El flujo de refrigerante se divide en dos canales a lo largo de la rama fría y caliente, los canales se conectarán a través de estructuras térmicas, de modo que al pasar por el canal, el refrigerante intercambia calor con diferentes canales. Simulando el flujo cruzado, el portador de calor caliente fluye de izquierda a derecha (ver Fig. 5) en cada canal, intercambiando calor secuencialmente con los canales del portador de calor frío, que va de abajo hacia arriba (ver Fig. 5). El punto más caliente está en la esquina superior izquierda, ya que el portador de calor caliente intercambia calor con el refrigerante ya calentado del canal frío. Y el más frío en la esquina inferior derecha, donde el refrigerante frío intercambia calor con el refrigerante caliente que ya se ha enfriado en la primera sección.

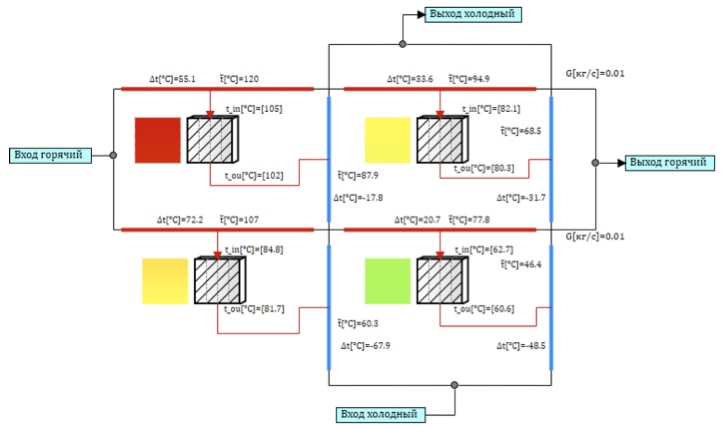
Figura 5. Un modelo de flujo cruzado de 4 celdas de diseño.

Dicho modelo para un intercambiador de calor de placas no tiene en cuenta la transferencia de calor entre las células debido a la conductividad térmica y no tiene en cuenta la mezcla del refrigerante, ya que cada canal está aislado.

Pero en nuestro caso, la última limitación no reduce la precisión, ya que en el diseño del intercambiador de calor, la membrana corrugada divide el flujo en muchos canales aislados a lo largo del refrigerante (ver Fig. 1). Veamos qué sucede con la precisión del cálculo al modelar un intercambiador de calor de placas con un aumento en el número de celdas de diseño.

Para el análisis de precisión, utilizamos dos opciones para dividir el intercambiador de calor en la celda de diseño:

1. Cada celda cuadrada contiene dos elementos hidráulicos (flujos frío y caliente) y uno térmico. (ver figura 5)
2. Cada celda cuadrada contiene seis elementos hidráulicos (tres secciones en flujos fríos y calientes) y tres elementos térmicos.

En el último caso, usamos dos tipos de conexión:

• contracorriente de corrientes frías y calientes;
• flujo asociado de flujo frío y caliente.

La corriente que se aproxima aumenta la eficiencia en comparación con el flujo cruzado, y la corriente asociada disminuye. Con una gran cantidad de celdas, se produce un promedio de flujo y todo se acerca al flujo transversal real a su alrededor (ver Figura 6).

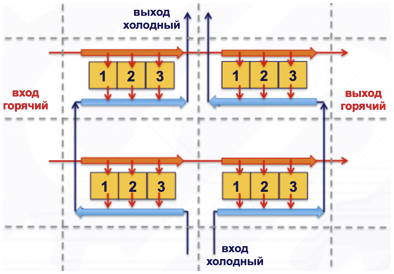
Figura 6. Un modelo de flujo cruzado de cuatro celdas con 3 elementos.

La Figura 7 muestra los resultados de una distribución de temperatura estacionaria en estado estacionario en el intercambiador de calor cuando se suministra aire a una temperatura de 150 ° C a lo largo de la línea caliente, y 21 ° C a lo largo de la línea fría, para varias opciones para dividir el modelo. El color y los números en la celda reflejan la temperatura promedio de la pared en la celda.

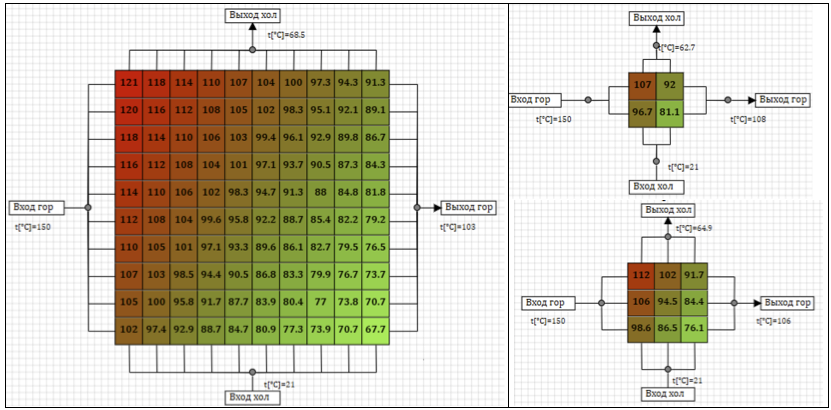
Figura 7. Temperaturas en estado estacionario para diferentes esquemas de cálculo.

La Tabla 2 muestra la temperatura de estado estable del aire calentado después del intercambiador de calor, dependiendo de la división del modelo del intercambiador de calor en celdas.

Tabla 2. Dependencia de la temperatura en el número de celdas de diseño en el intercambiador de calor.

Con un aumento en el número de celdas computacionales en el modelo, la temperatura final en estado estacionario aumenta. La diferencia entre la temperatura de estado estable en diferentes particiones puede considerarse como un indicador de precisión de cálculo. Se ve que con un aumento en el número de celdas de cálculo, la temperatura tiende al límite, y el aumento en la precisión no es proporcional al número de puntos de cálculo.

Surge la pregunta, pero ¿qué precisión del modelo necesitamos?

La respuesta a esta pregunta depende del propósito de nuestro modelo. Dado que este artículo trata sobre el diseño orientado a modelos, estamos creando un modelo para ajustar el sistema de control. Esto significa que la precisión del modelo debe ser comparable con la precisión de los sensores utilizados en el sistema.

En nuestro caso, la temperatura se mide mediante un termopar, en el que la precisión es de ± 2.5 ° C. Cualquier precisión mayor con el propósito de ajustar el sistema de control es inútil, nuestro sistema de control real simplemente "no lo verá". Por lo tanto, si suponemos que la temperatura límite con un número infinito de particiones es de 70 ° C, entonces un modelo que nos dé más de 67.5 ° C será de suficiente precisión. Todos los modelos con 3 puntos en la celda de cálculo y los modelos son más grandes que 5x5 con un punto en la celda. (Destacado en verde en la tabla 2)

Modos de funcionamiento dinámico

Para evaluar el modo dinámico, evaluamos el proceso de cambio de temperatura en los puntos más calientes y más fríos de la pared del intercambiador de calor para varios esquemas de diseño. (ver figura 8)


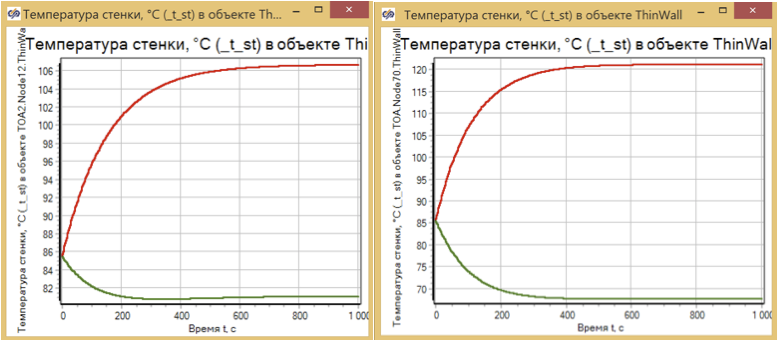
Figura 8. Calentamiento del intercambiador de calor. Modelos de dimensión 2x2 y 10x10.

Se puede ver que el tiempo del proceso de transición y su propia naturaleza, prácticamente no dependen del número de células calculadas, y están determinados únicamente por la masa del metal calentado.

Por lo tanto, concluimos que para una simulación honesta del intercambiador de calor en los modos de 20 a 150 ° C, con la precisión requerida por el sistema de control SCR, son suficientes unos 10-20 puntos calculados.

Experimente la configuración dinámica del modelo

, , , , , .

, , . 9 . , , , .

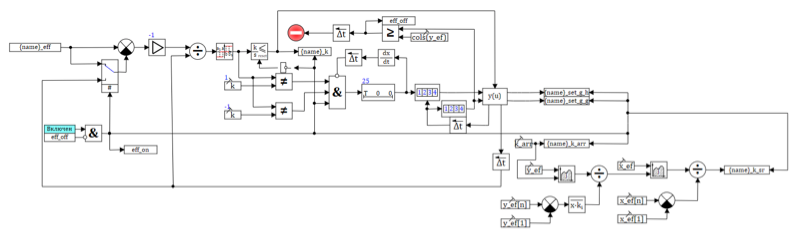
9. .

a . , ( ) . , 0.492 0.655

0.6, , , .

– :

:
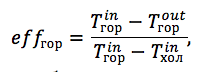
eff – ;
T ⁱⁿ – ;
T ^out – ;
T ⁱⁿ – .

3 .

3. %

. , , , , .

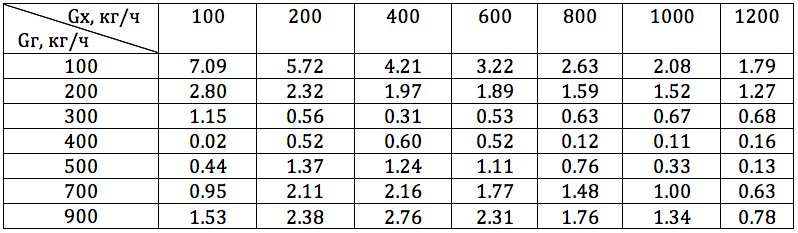
, 10 .

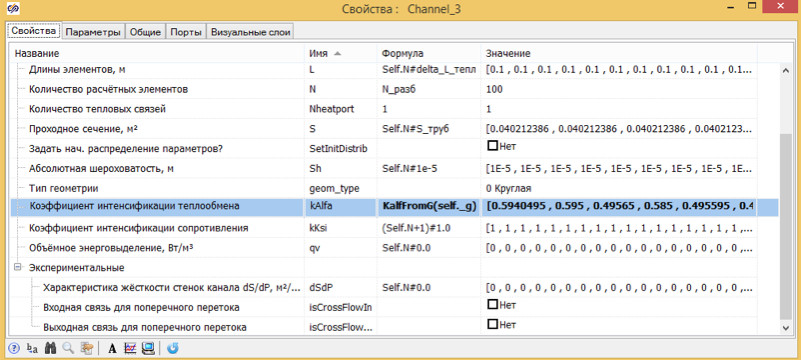
10. .

Conclusiones

• - .
  
• .
  
• .
  
• - !

. .