Serie "El ruido blanco dibuja un cuadrado negro"
La historia del ciclo de estas publicaciones comienza con el hecho de que en
el libro
de G. Sekey "Paradoxes in Probability Theory and Mathematical Statistics" (
p. 43 ), se descubrió la siguiente afirmación:

Fig. 1)
Según el análisis, el comentario sobre las primeras publicaciones (
parte 1 ,
parte 2 ) y el razonamiento posterior han madurado la idea de presentar este teorema en una forma más visual.
La mayoría de los miembros de la comunidad están familiarizados con el triángulo de Pascal, como consecuencia de la distribución de probabilidad binomial y muchas leyes relacionadas. Para comprender el mecanismo de la formación del triángulo de Pascal, lo expandiremos con más detalle, con el despliegue de los flujos de su formación. En el triángulo de Pascal, los nodos están formados por la relación de 0 y 1, la figura a continuación.
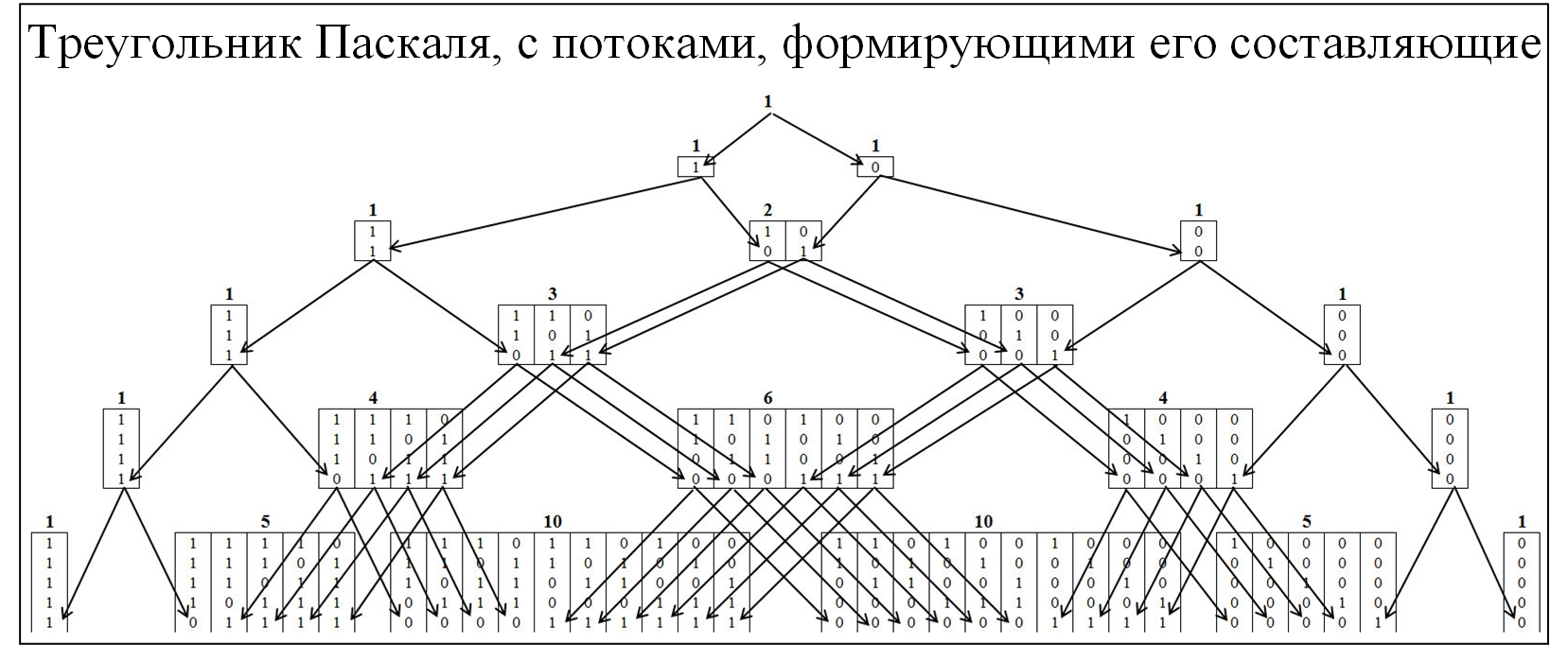
Fig. 2)
Para comprender el teorema de Erds-Renyi, compondremos un modelo similar, pero los nodos se formarán a partir de los valores en los que están presentes las cadenas más grandes, que consisten secuencialmente en los mismos valores. La agrupación se realizará de acuerdo con la siguiente regla: cadenas 01/10, para agrupar "1"; cadena 00/11, para agrupar "2"; cadenas 000/111, para agrupar "3", etc. En este caso, dividiremos la pirámide en dos componentes simétricos Figura 3.

Fig. 3)
Lo primero que llama la atención es que todos los movimientos se producen desde un grupo inferior a uno superior y viceversa. Esto es natural, ya que si se ha formado una cadena de tamaño j, ya no puede desaparecer.
Al determinar el algoritmo de concentración de números, logramos obtener la siguiente fórmula de recurrencia, cuyo mecanismo se muestra en las Figuras 4-6.
Denote los elementos en los que se concentran los números, donde n es el número de caracteres en el número (número de bits) y la longitud de la cadena máxima es m. Y cada elemento recibirá un índice n; mJ.
Denota que el número de elementos pasó de n; mJ a n + 1; m + 1J, n; mjn + 1; m + 1.

Fig. 4)
La Figura 4 muestra que para el primer grupo no es difícil determinar los valores de cada fila. Y esta dependencia es igual a:

Fig. 5)
Determinamos para el segundo grupo, con la longitud de la cadena m = 2, Figura 6.
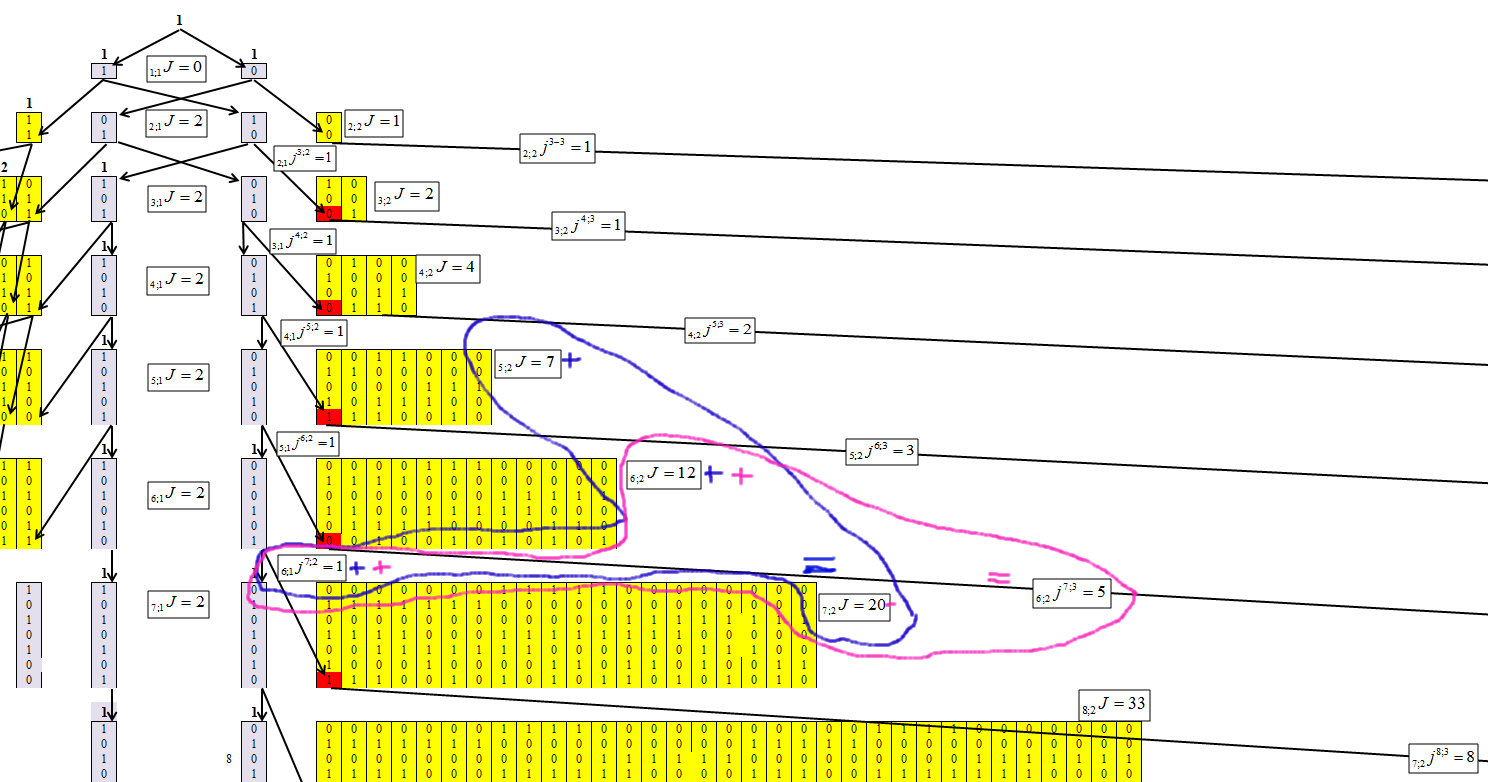
Fig. 6)
La Figura 6 muestra que para el segundo grupo, la dependencia es igual a:

Fig. 7)
Determinamos para el tercer grupo, con la longitud de la cadena m = 3, Figura 8.
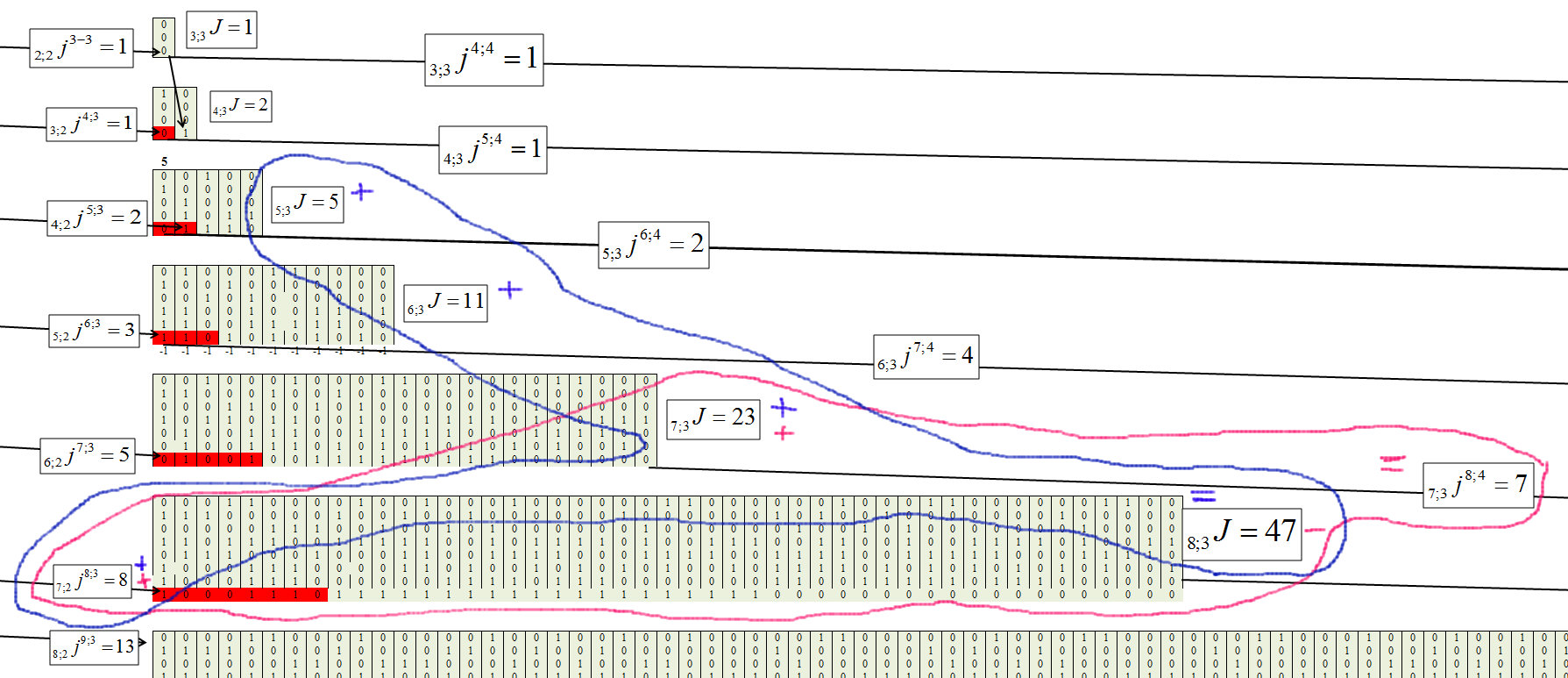
Fig. 8)

Fig. 9)
La fórmula general de cada elemento toma la forma:

Fig. 10)

Fig. 11)
Verificación
Para la verificación, utilizamos la propiedad de esta secuencia, que se muestra en la Figura 12. Consiste en el hecho de que los últimos miembros de una línea desde una determinada posición toman un solo valor para todas las líneas con una longitud de línea creciente.
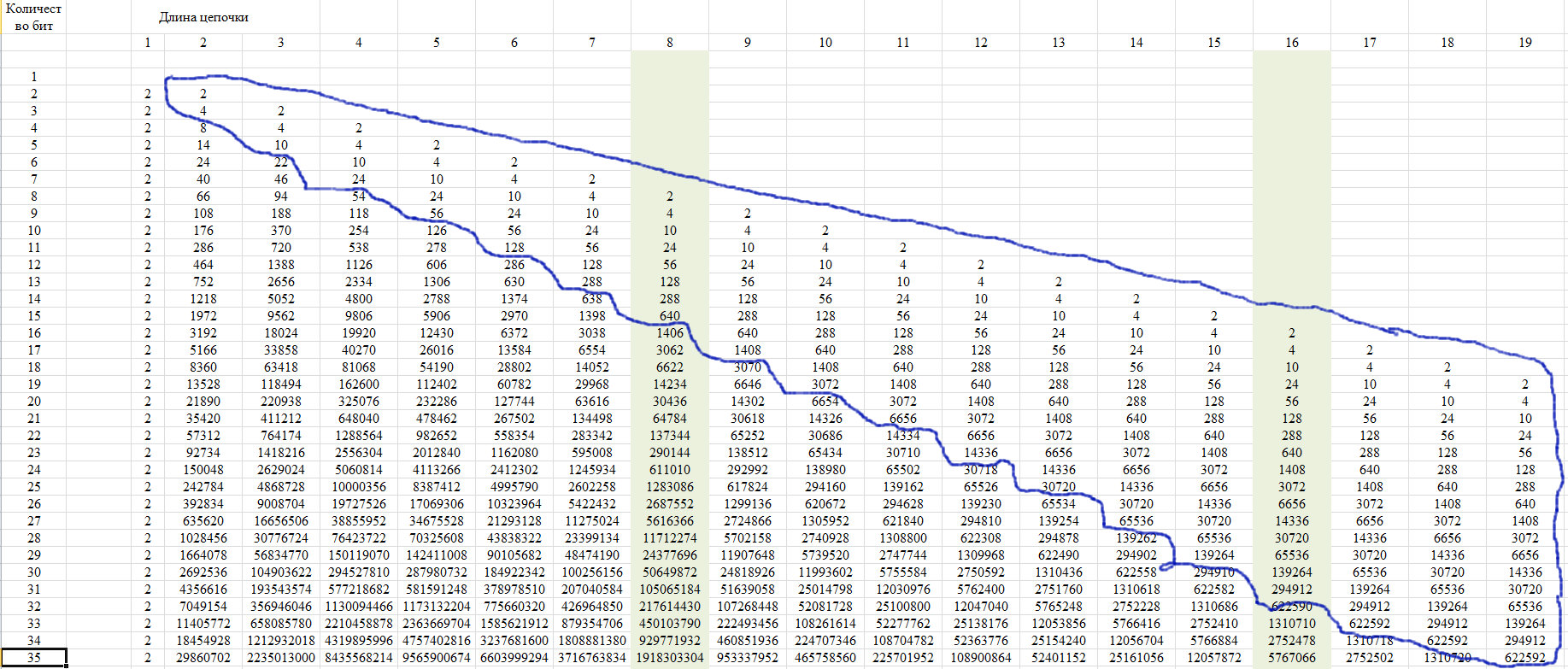
Fig. 12)
Esta propiedad se debe al hecho de que con una longitud de cadena de más de la mitad de la fila completa, solo es posible una de esas cadenas. Mostramos esto en el diagrama de la Figura 13.

Fig. 13)
En consecuencia, para valores de k <n-2, obtenemos la fórmula:
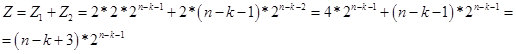
Fig. 14)
De hecho, el valor de Z es el número potencial de números (opciones en una cadena de n bits) que contienen una cadena de k elementos idénticos. Y de acuerdo con la fórmula de recurrencia, determinamos el número de números (opciones en una cadena de n bits) en los que la cadena de k elementos idénticos es la más grande. Por ahora, supongo que el valor Z es virtual. Por lo tanto, en la región n / 2, pasa al espacio real. En la Figura 15, una pantalla con cálculos.

Fig. 15)
Permítanos mostrar un ejemplo de una palabra de 256 bits, que puede determinarse mediante este algoritmo.

Fig. 16)
Si lo determinan los estándares de confiabilidad del 99.9% para el GSPCH, entonces la clave de 256 bits debe contener cadenas consecutivas de caracteres idénticos con un número del 5 al 17. Es decir, de acuerdo con los estándares del GSPCH, para que cumpla con el requisito de similitud de aleatoriedad con una confiabilidad del 99.9%, GSPCH, en las pruebas de 2000 (emitiendo un resultado en forma de un número binario de 256 bits) solo debería dar un resultado en el que la longitud máxima de la serie de los mismos valores: menos de 4 o más de 17.
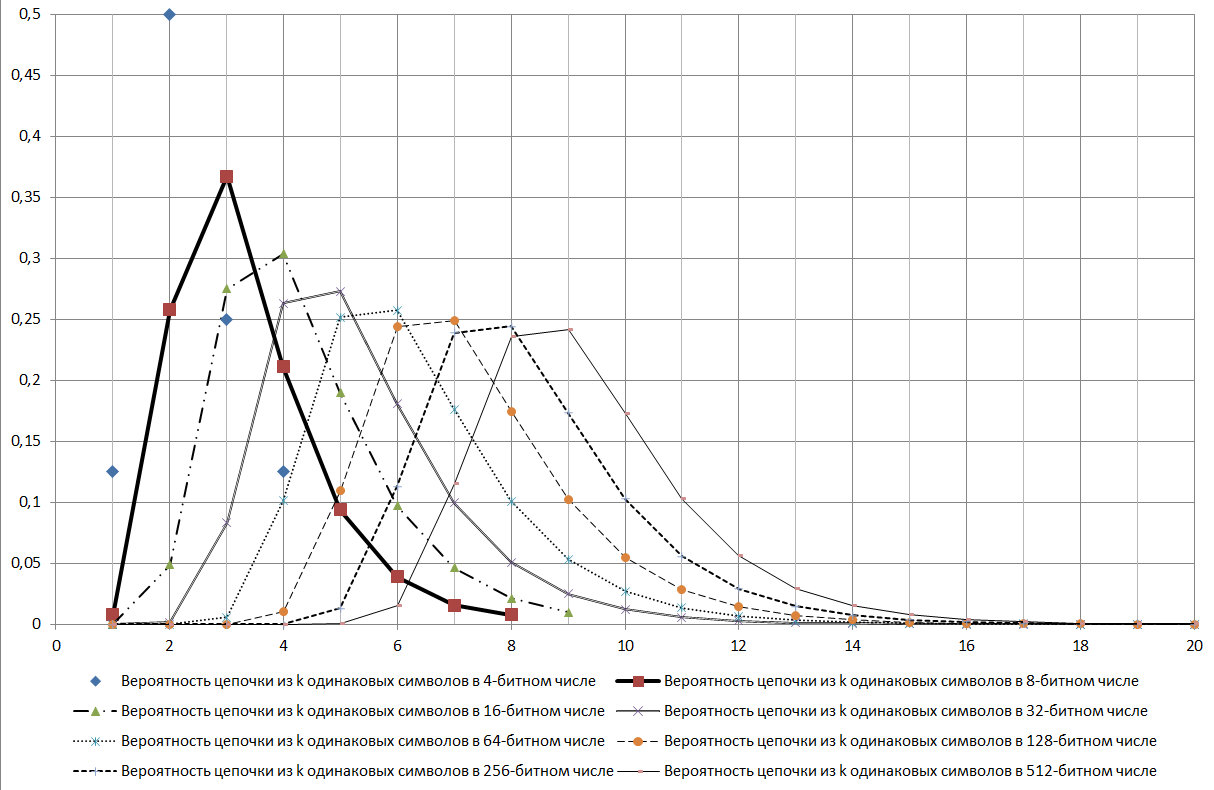
Fig. 17)
Como se puede ver en el diagrama que se muestra en la Figura 17, la cadena log2N es un modo para la distribución en consideración.
Durante el estudio, se encontraron muchos signos de varias propiedades de esta secuencia. Aquí hay algunos de ellos:
- debe ser bien probado por el criterio de chi-cuadrado;
- da signos de la existencia de propiedades fractales;
- pueden ser buenos criterios para identificar varios procesos aleatorios.
Y muchas más otras conexiones.
Se verificó si dicha secuencia también existe en la
Enciclopedia en línea de secuencias enteras (OEIS) (Enciclopedia en línea de secuencias
enteras ) en el número de secuencia
A006980 , se hace referencia a la publicación
JL Yucas, Contando conjuntos especiales de palabras binarias Lyndon, Ars Combin. 31 (1991), pág. 21-29 , donde la secuencia se muestra en la página 28 (en la tabla). En la publicación, las líneas están numeradas 1 menos, pero los valores son los mismos. En general, la publicación trata sobre las
palabras de Lyndon , es
decir , es muy posible que el investigador ni siquiera sospechara que esta serie estaba relacionada con este aspecto.
Volvamos al teorema de Erds-Renyi. De acuerdo con los resultados de esta publicación, se puede decir que en la formulación presentada, este teorema se refiere al caso general, que está determinado por el teorema de Muavre-Laplace. Y el teorema indicado, en esta formulación, no puede ser un criterio inequívoco para la aleatoriedad de una serie. Pero la fractalidad, y para este caso se expresa que las cadenas de la longitud indicada pueden combinarse con cadenas de mayor longitud, no nos permiten rechazar este teorema tan inequívocamente, ya que es posible una inexactitud en la formulación. Un ejemplo es el hecho de que si, para uno de 256 bits, la probabilidad de un número donde la cadena máxima de 8 bits es 0.244235, entonces, junto con las otras secuencias más largas, la probabilidad de que haya un número de 8 bits en el número ya es - 0.490234375. Es decir, hasta ahora, no hay una oportunidad inequívoca de rechazar este teorema. Pero este teorema encaja bastante bien en otro aspecto, que se mostrará más adelante.
Aplicación práctica
Veamos el ejemplo presentado por el usuario de VDG:
“... Las ramas dendríticas de una neurona se pueden representar como una secuencia de bits. Una rama, y luego toda la neurona, se activa cuando se activa una cadena de sinapsis en cualquiera de sus lugares. La neurona tiene la tarea de no responder al ruido blanco, respectivamente, la longitud mínima de la cadena, por lo que recuerdo con Numenty, es de 14 sinapsis en la neurona piramidal con sus 10 mil sinapsis. Y de acuerdo con la fórmula que obtenemos: Log_ {2} 10000 = 13.287. Es decir, se producirán cadenas de menos de 14 de longitud debido al ruido natural, pero no activarán la neurona. Está perfectamente establecido " .
Construiremos un gráfico, pero teniendo en cuenta el hecho de que Excel no considera valores superiores a 2 ^ 1024, nos limitaremos al número de sinapsis 1023 y, teniendo esto en cuenta, interpolaremos el resultado por comentario, como se muestra en la Figura 18.

Fig. 18)
Hay una red neuronal biológica que funciona cuando se compila una cadena de m = log2N = 11. Esta cadena es un valor modal y se alcanza un valor umbral, la probabilidad, de algún tipo de cambio en la situación de 0,78. Y la probabilidad de error es 1- 0.78 = 0.22. Supongamos que funciona una cadena de 9 sensores, donde la probabilidad de determinar el evento es 0.37, respectivamente, la probabilidad de error es 1 - 0.37 = 0.63. Es decir, para lograr una disminución en la probabilidad de error de 0.63 a 0.37, es necesario que funcionen 3.33 cadenas de 9 elementos. La diferencia entre 11 y 9 elementos es de segundo orden, es decir 2 ^ 2 = 4 veces, que si se redondea a enteros, ya que los elementos dan un valor entero, entonces 3.33 = 4. Buscamos reducir el error al procesar una señal de 8- elementos, ya necesitamos 11 cadenas de activación de 8 elementos. Supongo que este es un mecanismo que le permite evaluar la situación y tomar una decisión sobre cambiar el comportamiento de un objeto biológico. Razonable y eficientemente suficiente, en mi opinión. Y teniendo en cuenta el hecho de que sabemos acerca de la naturaleza que utiliza los recursos de la manera más económica posible, la hipótesis de que el sistema biológico utiliza este mecanismo está justificada. Y cuando entrenamos la red neuronal, de hecho, reducimos la probabilidad de error, ya que para eliminar completamente el error necesitamos encontrar una relación analítica.
Pasamos al análisis de datos numéricos. En el análisis de datos numéricos, tratamos de elegir una dependencia analítica en la forma y = f (xi). Y en la primera etapa la encontramos. Después de encontrarlo, las series existentes se pueden representar como binarias, en relación con la ecuación de regresión, donde asignamos 1 a valores positivos y 0 a valores negativos, y luego analizamos una serie de elementos idénticos. Determinamos la distribución más grande, a lo largo de la cadena, de cadenas más cortas.
Luego, pasamos al teorema de Erdos-Renyi, se deduce que al realizar una gran cantidad de pruebas de un valor aleatorio, se debe formar una cadena de elementos idénticos en todos los registros del número generado, es decir, m = log2N. Ahora, cuando examinamos los datos, no sabemos cuál es realmente el volumen de la serie. Pero si mira hacia atrás, esta cadena máxima nos da razones para suponer que R es un parámetro que caracteriza un campo de variable aleatoria, Figura 19.
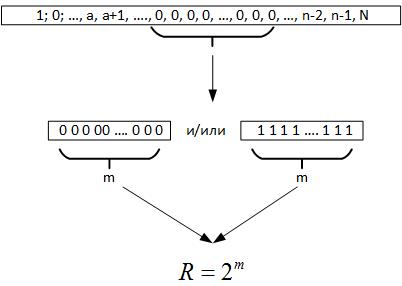
Fig. 19)
Es decir, comparando R y N, podemos sacar varias conclusiones:
- Si R <N, entonces el proceso aleatorio se repite varias veces en datos históricos.
- Si R> N, entonces el proceso aleatorio tiene una dimensión más alta que los datos disponibles, o determinamos incorrectamente la ecuación de la función objetivo.
Luego, para el primer caso, estamos diseñando una red neuronal con sensores de 2 ^ m, supongo que podemos agregar un par de sensores para captar las transiciones, y entrenamos esta red en datos históricos. Si la red como resultado del entrenamiento no puede aprender y producirá el resultado correcto con una probabilidad del 50%, entonces esto significa que la función objetivo encontrada es óptima y es imposible mejorarla. Si la red puede aprender, mejoraremos aún más la dependencia analítica.
Si la dimensión de la serie es mayor que la dimensión de una variable aleatoria, entonces se puede usar la propiedad de fractalidad de la variable aleatoria, ya que cualquier serie de tamaño m contiene todos los subespacios de dimensiones inferiores. Supongo que en este caso tiene sentido entrenar la red neuronal en todos los datos, excepto en las cadenas m.
Otro enfoque para el diseño de redes neuronales puede ser el período de pronóstico.
En conclusión, debe decirse que, en el camino a esta publicación, se descubrieron muchos aspectos en los que la magnitud de la dimensión de una variable aleatoria y sus propiedades descubiertas se cruzaban con otras tareas en el análisis de los datos. Pero por ahora, todo esto está en una forma muy cruda y se dejará para futuras publicaciones.
Parte anterior:
Parte 1 ,
Parte 2