Posit-aritmética: derrotando un punto flotante en su propio campo. Parte 2

Parte 1

4. Comparación cuantitativa de sistemas numéricos.

4.1. Precisión decimal

La precisión es lo opuesto al error. Si tenemos un par de números x e y (signo distinto de cero y uno), la distancia entre ellos en orden de magnitud es $$$\ mid log_ {10} (x / a) \ mid$ órdenes decimales, esta es la misma medida que define el rango dinámico entre los números positivos representables más pequeños y más grandes x e y. La distribución ideal de diez números entre 1 y 10 en un sistema de números reales no sería una distribución uniforme de números en orden del 1 al 10, sino exponencial: $$$1, 10 ^ {1/10}, 10 ^ {2/10}, ..., 10 ^ {9/10}, 10$ . Esta es la escala de decibelios utilizada por los ingenieros durante mucho tiempo para expresar relaciones, por ejemplo, 10 decibelios es una relación de diez veces. 30db significa coeficiente $$$10 ^ 3 = 1000$ . La relación de 1db es un factor de aproximadamente 1.26, si conoce el valor con una precisión de 1db, tiene una precisión de 1 decimal. Si conoce el valor con una precisión de 0.1 db, esto significa 2 signos de precisión, etc. La fórmula de precisión decimal es $$$log_ {10} (1 / \ mid log_ {10} (x / y) \ mid) = - log_ {10} (\ mid log_ {10} (x / y) \ mid)$ , donde x e y son valores válidos calculados mediante sistemas de redondeo, como los utilizados en formatos flotante y positivo, o límites superior e inferior si se utilizan sistemas estrictos que utilizan intervalos, o valores válidos.

4.2. Definición de conjuntos de comparación flotante y positiva

Podemos crear modelos a escala de números flotantes y positivos cada 8 bits de largo. La ventaja de este enfoque es que 256 valores son un conjunto lo suficientemente pequeño como para que podamos probarlo completamente y comparar todo $$$256 ^ 2$ ocurrencias en tablas para operaciones de suma, resta, multiplicación y división. Los números reales con una precisión de 1/4 tienen un bit de signo, cuatro bits del exponente y tres bits de la parte fraccionaria, y se adhieren a todas las reglas del IEEE 754. El número positivo más pequeño (desnormalizado) es 1/1024, el mayor positivo es 240, el rango dinámico es asimétrico e igual. 5.1 órdenes decimales.14 combinaciones de bits representan NaN.

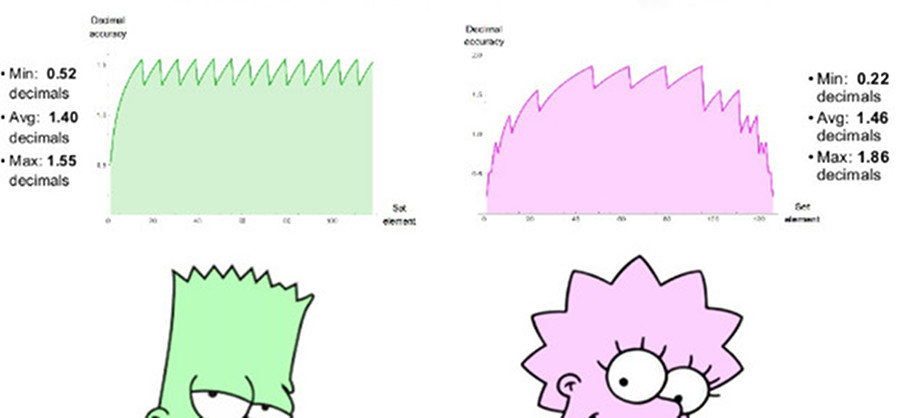
Un positivo comparable de 8 bits usa es = 1, tiene un rango de números positivos de 1/4096 a 4096, un rango dinámico simétrico de 7.2 órdenes decimales. No hay valores de NaN. Podemos trazar gráficos de precisión decimal de números positivos en ambos conjuntos, como se muestra en la fig. 7. Tenga en cuenta que los valores representados por números positivos tienen un rango dinámico de dos órdenes decimales de magnitud mayor que los números flotantes, y la precisión es la misma o mayor para todos los valores, excepto aquellos en los que los números flotantes están cerca del desbordamiento o anti-desbordamiento. La sangría de los gráficos para ambos sistemas es una aproximación logarítmica de una función lineal por partes. En números flotantes, la precisión disminuye solo a la izquierda, en el área cercana a la antipersonalidad, a la derecha, la función se interrumpe, porque luego vienen los valores de NaN. Los números positivos tienen una función de precisión decreciente más simétrica alrededor de los bordes.


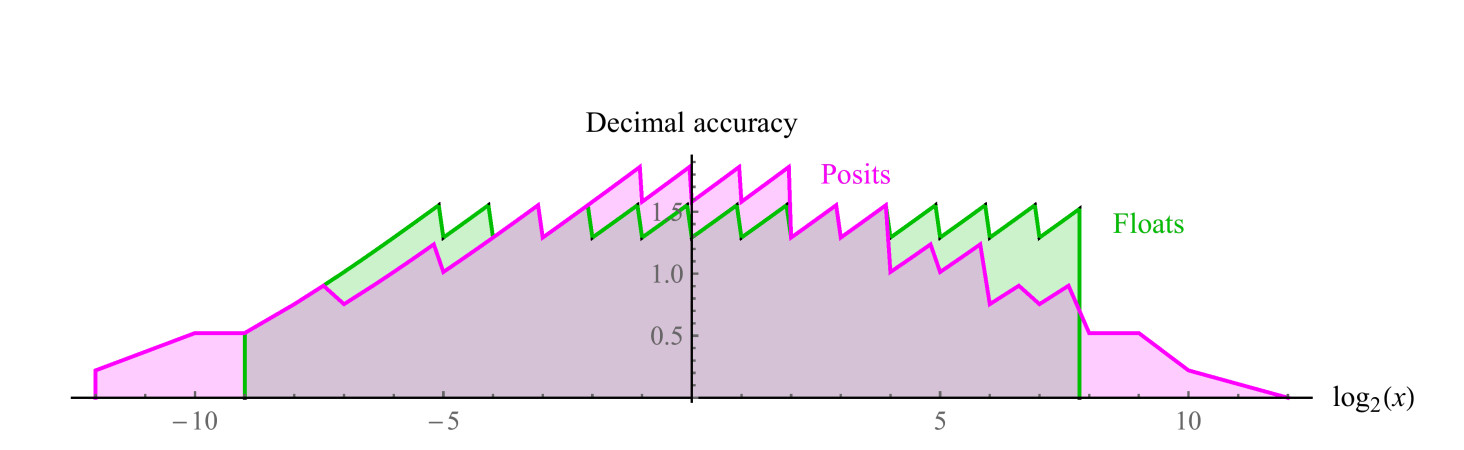
Fig. 7. Comparación de la precisión decimal de números flotantes y positivos

4.3. Comparar operaciones de argumento único

4.3.1. Valor inverso

Para cada posible valor de entrada x de la función 1 / x, el resultado puede corresponder exactamente a otro valor en el conjunto dado, o puede redondearse, en este caso podemos medir el error decimal usando la fórmula de la sección 4.1, para números flotantes, el resultado puede conducir a un desbordamiento o NaN. Ver fig. 8)



Fig. 8. Comparación cuantitativa de números flotantes y positivos al calcular el valor inverso

Las curvas en el gráfico de la derecha muestran la magnitud del error al calcular el valor inverso, mientras que los números flotantes pueden dar como resultado NaN. Los números de posición son superiores a flotar en una gran cantidad de casos, y esta superioridad se mantiene en todo el rango. Calcular el inverso de los números flotantes desnormalizados provoca un desbordamiento, lo que conduce a un valor de error infinito y, por supuesto, el argumento NaN da el inverso del NaN. Los números positivos se cierran en relación con el cálculo del valor inverso.

4.3.2. Raíz cuadrada

La función de raíz cuadrada no conduce a desbordamiento o anti-desbordamiento. Para argumentos negativos y para NaN, el resultado será NaN. Recuerde que tenemos un "modelo a escala" de números flotantes y positivos, las ventajas de los positivos aumentan con el aumento de la precisión de los datos. Para flotante y positivo de 64 bits, el error positivo será aproximadamente 1/30 del error flotante, en lugar de 1/2.

4.3.3. Square

Otra operación unaria común es $$$x ^ 2$ . Los desbordamientos y los anti-desbordamientos son comunes al cuadrar una carroza. Para casi la mitad de un flotador, la cuadratura no produce un resultado significativo, mientras que cuadrar el número positivo en un cuadrado siempre produce el número positivo (un cuadrado de infinito sin signo es un infinito sin signo).


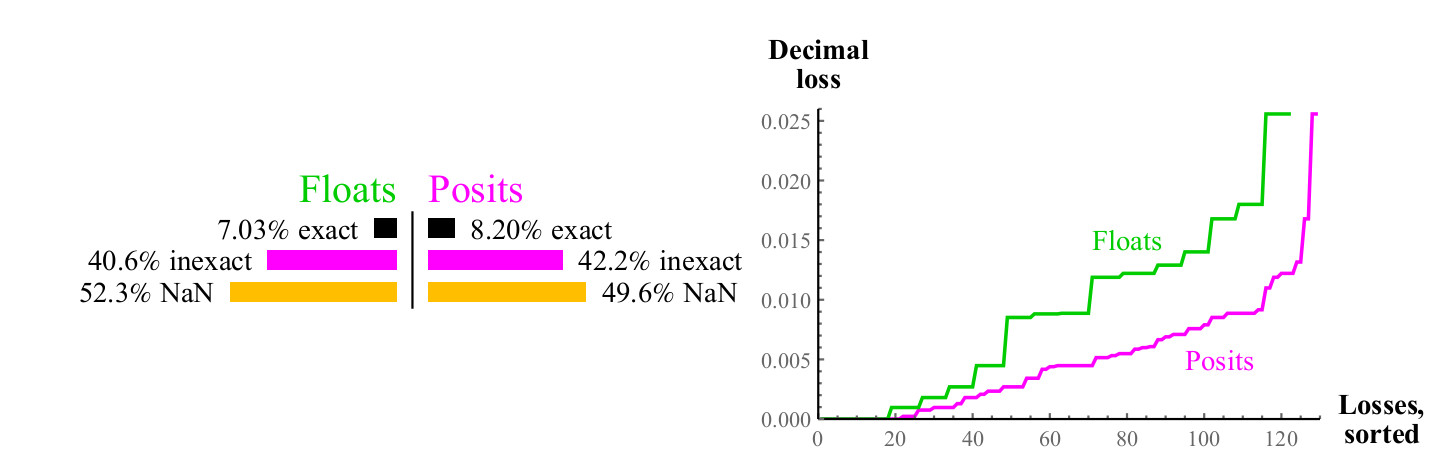
Fig. 9. Comparación cuantitativa de números flotantes y positivos al calcular $$$\ sqrt x$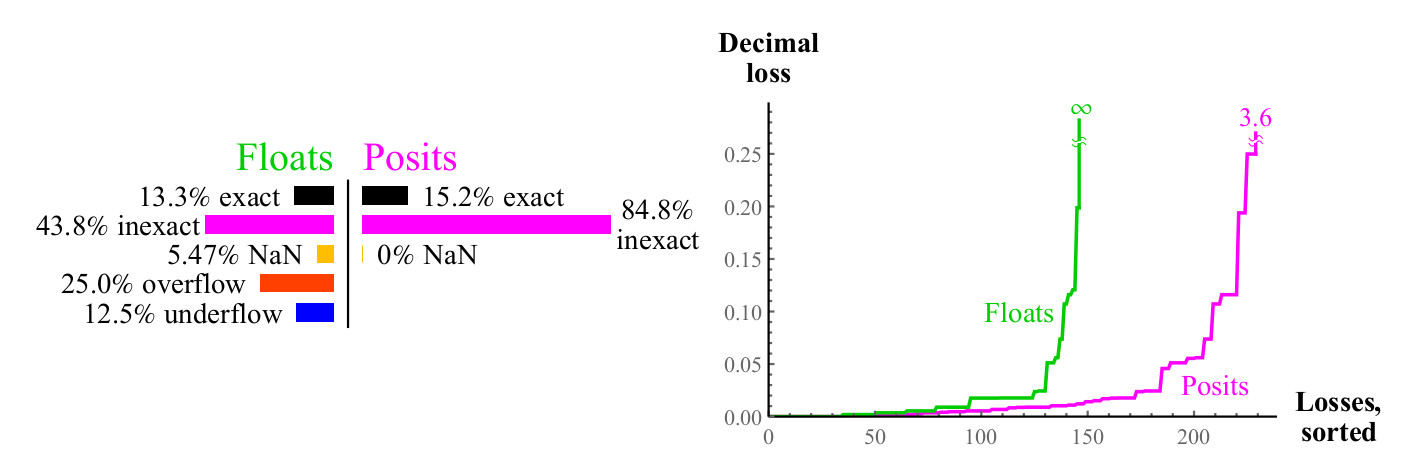


Fig. 10. Comparación cuantitativa de números flotantes y positivos al calcular $$$x ^ 2$

4.3.4 Base 2 Logaritmo

También hicimos una comparación para cubrir la función de logaritmo de base 2, es decir, el porcentaje de casos en los que $$$log_2 (x)$ puede representarse con precisión y, si no puede representarse con precisión, cuántos decimales perdemos. Los números flotantes tienen la única ventaja en este caso: se pueden usar para representar $$$log_2 (0)$ como $$$- \ infty$ y $$$log_2 (\ infty)$ como $$$\ infty$ , pero esto está más que compensado por un gran diccionario de potencias enteras de dos para números positivos.


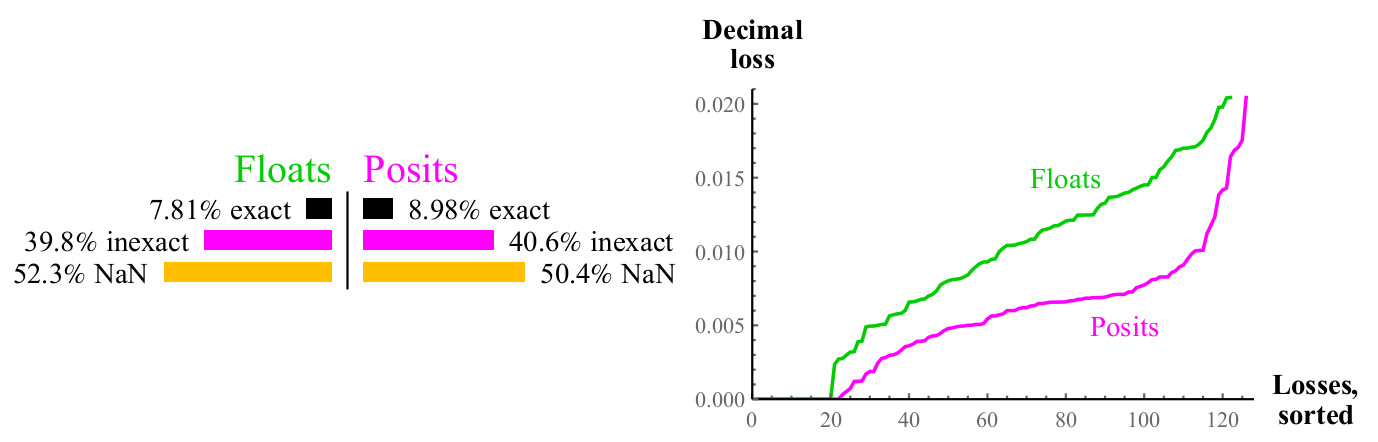
Fig. 11. Comparación cuantitativa de números flotantes y positivos al calcular $$$log_2 (x)$

El gráfico es similar al de la raíz cuadrada, aproximadamente la mitad de los casos dan NaN en ambos casos, pero los números positivos tienen la mitad de la pérdida de precisión decimal. Si puedes calcular $$$log_2 (x)$ , solo necesita multiplicar el resultado por un factor de escala para obtener $$$ln (x)$ o $$$log_ {10} (x)$ o logaritmo con cualquier otra razón.

4.3.5. Expositor $$$2 ^ x$

Del mismo modo, si puedes calcular $$$2 ^ x$ , puede usar fácilmente el factor de escala para obtener $$$e ^ x$ o $$$10 ^ x$ etc. Los números de posición tienen una excepción, $$$2 ^ x$ es igual a NaN cuando el argumento es $$$\ pm \ infty$ .


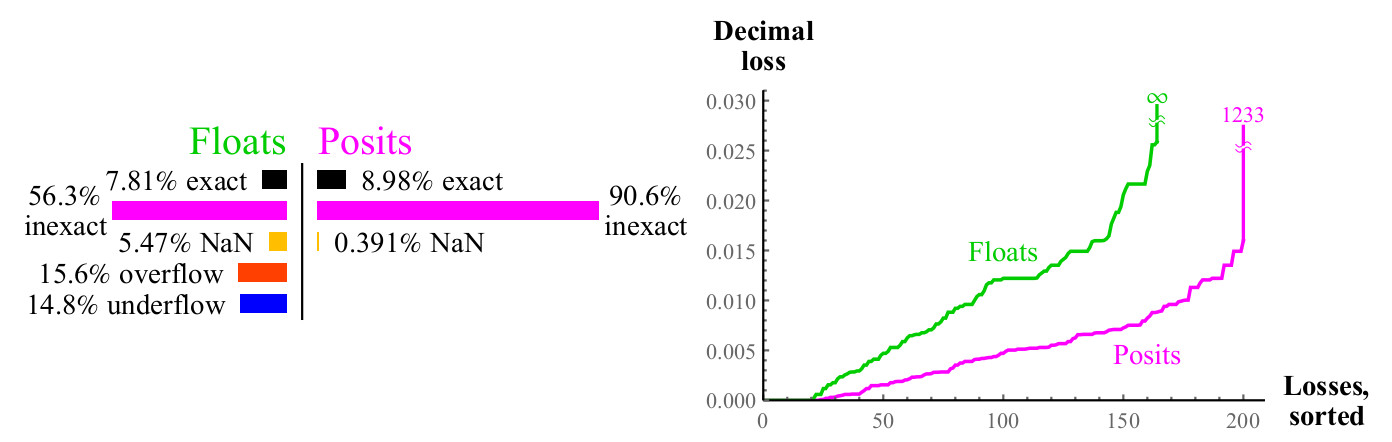
Fig. 12. Comparación cuantitativa de números flotantes y positivos al calcular $$$2 ^ x$

La pérdida decimal máxima para los números positivos puede parecer grande ya que $$$2 ^ {maxpos}$ será redondeado de nuevo a maxpos. En este ejemplo, solo un pequeño número de errores es tan grande como $$$log_ {10} (24096) \ aprox1233$ órdenes decimales Decide cuál es mejor: ¿perder más de mil órdenes decimales o perder un número infinito de órdenes decimales? Si no puede usar números tan grandes, los números positivos siguen ganando, porque los errores con valores pequeños son mucho mejores. En todos los casos cuando pierde una gran cantidad de órdenes decimales cuando usa números positivos, el argumento de entrada va mucho más allá de lo que los números flotantes pueden expresar . Los gráficos muestran cómo los números positivos son más estables en términos del rango dinámico en el que el resultado tiene sentido, y son superiores en precisión dentro de este rango.

Para operaciones ordinarias unarias $$$1 / x, \ sqrt x, x ^ 2, log_2 (x)$ y $$$2 ^ x$ , los números positivos son completamente e invariablemente más precisos que los números flotantes con el mismo número de bits, y producen resultados significativos en un amplio rango dinámico. Ahora dirigimos nuestra atención a cuatro operaciones aritméticas elementales que tienen dos argumentos: suma, resta, multiplicación y división.

4.4. Comparar las operaciones de dos argumentos.

Podemos usar el modelo a escala de un sistema de números para estudiar las operaciones aritméticas de dos argumentos, como la suma, la resta, la multiplicación y la división. Para visualizar los resultados de 65536, creamos un "gráfico de cobertura" de 256 * 256, que muestra claramente qué proporción de los resultados es precisa, inexacta, causa desbordamiento, anti-desbordamiento o NaN.

4.4.1. Suma y resta

Desde $$$x - y = x + (- y)$ funciona muy bien tanto para flotante como para positivo, no hay necesidad de estudiar la resta por separado. Para la operación de suma, calculamos el valor exacto $$$z = x + y$ y compárelo con la cantidad devuelta en cada uno de los sistemas numéricos. Puede suceder que el resultado sea inexacto, luego se debe redondear al número finito distinto de cero, desbordamiento o anti-desbordamiento, o incertidumbre de la forma $$$\ infty- \ infty$ lo que resulta en NaN. Cada uno de estos casos está marcado en color, y podemos cubrir toda la tabla de suma de un vistazo. En el caso de redondear los resultados, el color cambia de negro (valor exacto) a púrpura (valor exacto para posit y float). Fig. 13 muestra cómo se ve el gráfico de cobertura para números flotantes y unum. Al igual que con las operaciones unarias, pero con muchos más puntos, podemos sacar conclusiones sobre la capacidad de cada sistema de números para dar respuestas significativas y precisas:


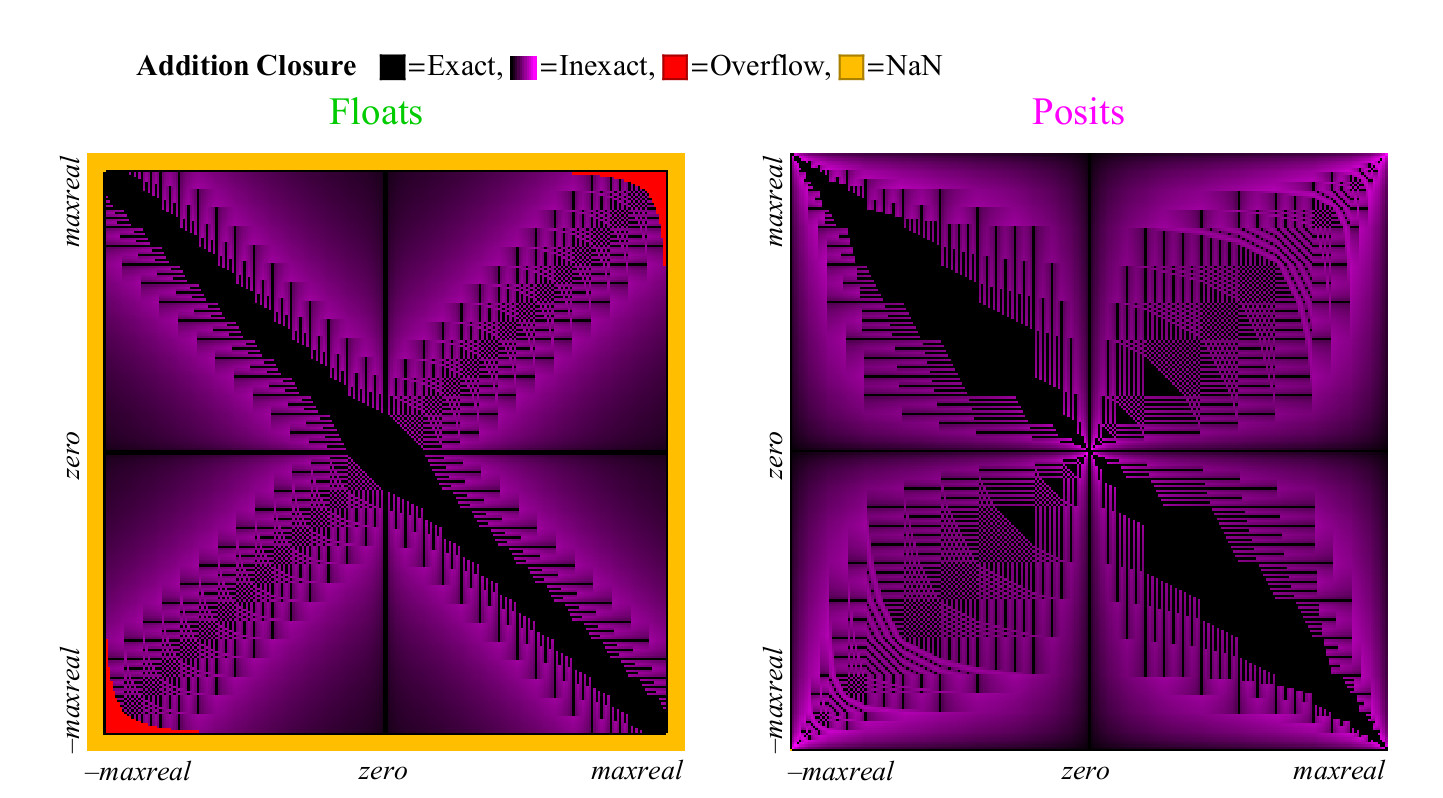
Fig. 13. Gráfico de cobertura completa para agregar números flotantes y positivos


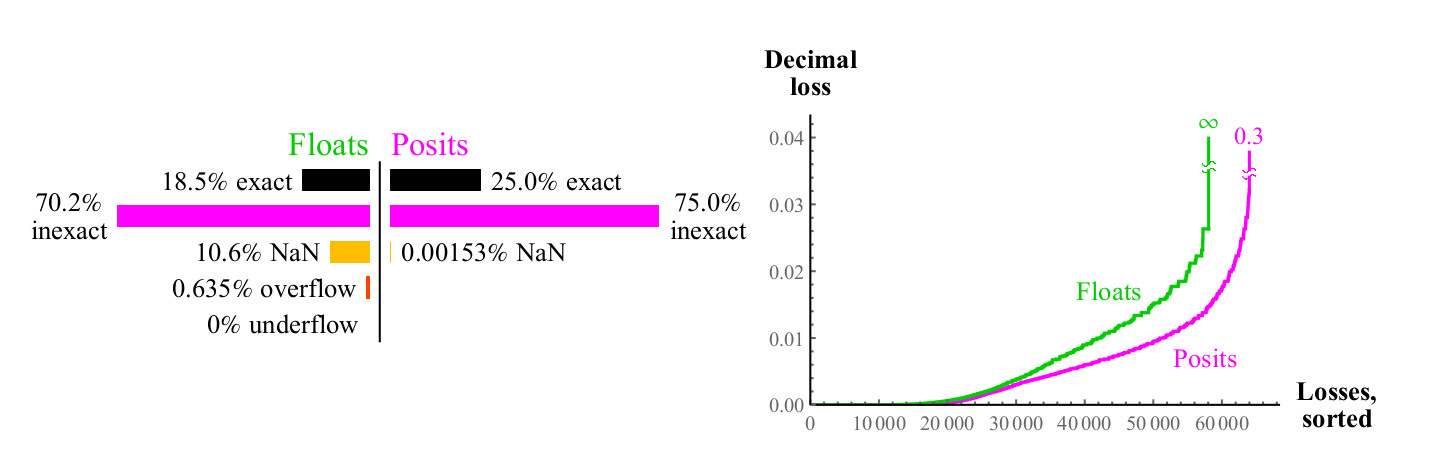
Fig. 14. Comparación cuantitativa de números flotantes y positivos para la suma

A primera vista, resulta obvio que posit tiene significativamente más puntos en el gráfico de adición en el que el resultado es preciso. La franja diagonal negra ancha en el gráfico de cobertura para flotación es mucho más ancha de lo que será para una mayor precisión, ya que representa una zona de números desnormalizados en la que los números de flotación están espaciados a intervalos iguales, como los números de punto fijo, tales números constituyen una gran proporción del número total solo en el caso de números de 8 bits.

4.4.2. Multiplicación

Utilizamos un enfoque similar para comparar qué tan bien se multiplican los números flotante y positivo. A diferencia de la adición, la multiplicación puede causar un desbordamiento de los números flotantes. “Anti-desbordamiento gradual”, la zona que puede ver en el centro en la Fig. 15. a la izquierda (es decir, números desnormalizados. aprox. transl. ) Sin esta zona, la zona azul antidesbordamiento tendría forma de diamante. El gráfico de multiplicación para los números positivos es menos colorido, lo cual es mejor. Solo dos píxeles se resaltan como NaN, cerca del lugar donde se encuentra la marca cero de los ejes (los píxeles se encuentran más a la izquierda en el centro verticalmente y la parte inferior en el centro horizontalmente. Aprox. Transl. ) Hay resultados de multiplicación $$$\ pm \ infty \ cdot 0 = NaN$ . Los números flotantes tienen más casos en los que el producto es preciso pero a un precio terrible. Como se muestra en la Fig. 15, casi 1/4 de todos los productos de flotación conducen a desbordamiento o antidesbordamiento, y esta fracción no disminuye al aumentar la precisión del flotador.


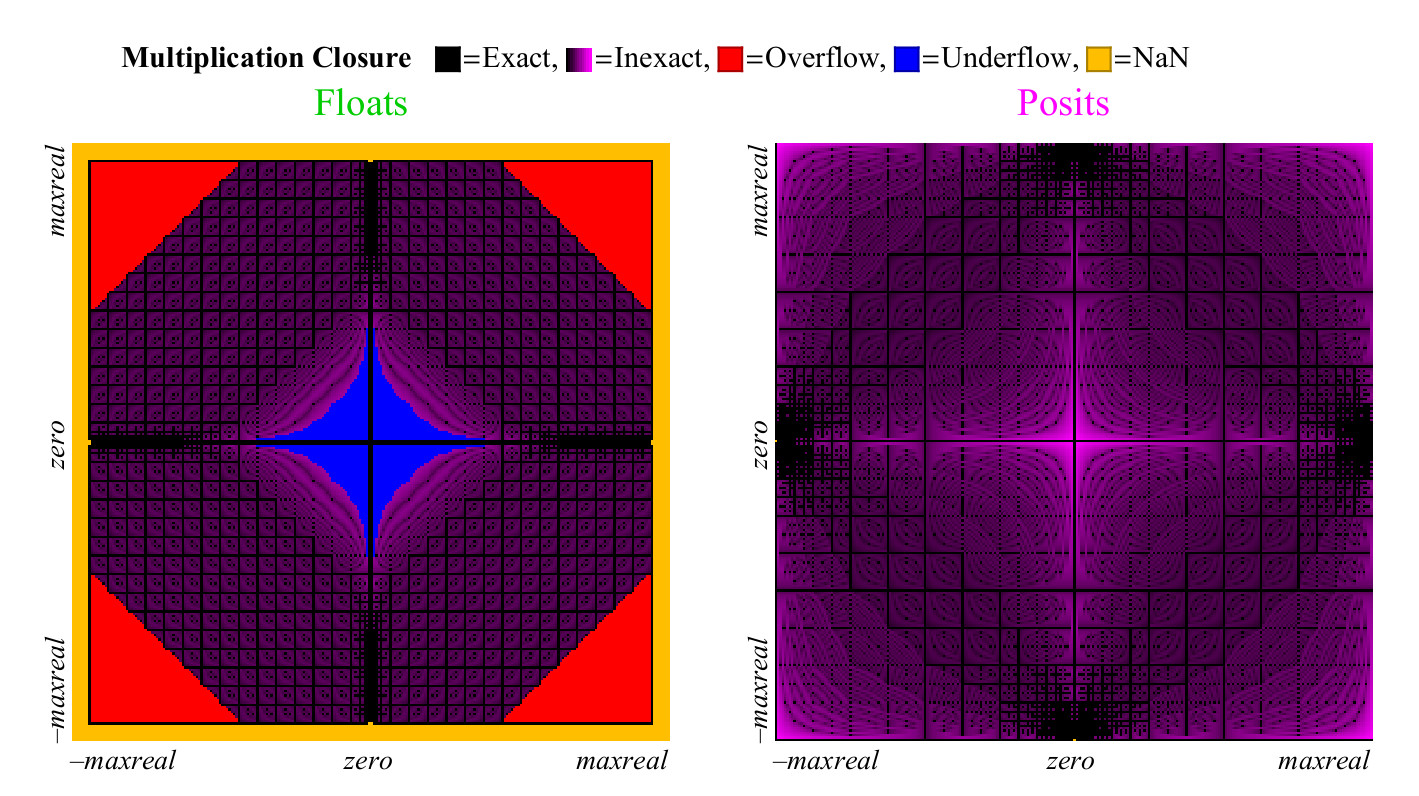
Figura 15. Gráfico de cobertura completa para multiplicar números flotantes y positivos

El peor caso de redondeo para números positivos ocurre cuando $$$maxpos \ veces maxpos$ que se redondea nuevamente a maxpos. Para tales casos (muy raro), el error es 3.6 órdenes decimales. Como el gráfico de la fig. 16, los números positivos son significativamente mejores que flotantes, minimizan el error de multiplicación.


Fig. 16. Comparación cuantitativa de números flotantes y positivos para multiplicación

El gráfico de cobertura para la operación de división es similar al gráfico para la multiplicación, pero las zonas se intercambian, para ahorrar espacio, no se muestra aquí. Los indicadores cuantitativos para la división son casi los mismos que para la multiplicación.

4.5. Comparación de números flotantes y positivos para evaluar expresiones

4.5.1 Pruebe el "presupuesto de precisión de 32 bits"

Las pruebas generalmente se realizan en función del tiempo de ejecución mínimo y, a menudo, no ofrecen una imagen completa de la precisión del resultado. Otro tipo de prueba es aquella en la que arreglamos el presupuesto del error, es decir, el número de bits por variable e intentamos obtener la máxima precisión decimal como resultado. Aquí hay un ejemplo de una expresión que podemos usar para comparar sistemas numéricos con un presupuesto de 32 bits por número:

$$

$$X = \ left (\ dfrac {27/10-e} {\ pi - (\ sqrt 2+ \ sqrt 3)} \ right) ^ {67/16} = 302.8827196 \ dotsb$$

La regla es que comenzamos con la mejor representación de números $$$\ pi$ y $$$e$ , posible en cada uno de los sistemas numéricos y representaciones de todos los enteros indicados, y vemos cuántos dígitos decimales coinciden con el valor verdadero de X después de realizar nueve operaciones en la expresión. Destacaremos los números incorrectos en naranja .

A pesar de que los números flotantes IEEE de 32 bits tienen una precisión decimal, que oscila entre 7.3 y 7.6 órdenes decimales, la acumulación de errores de redondeo en el cálculo de X da una respuesta de 302. 912 , que tiene solo tres dígitos válidos. Esta es una de las razones por las que los usuarios sienten la necesidad de usar flotante de 64 bits en todas partes, ya que incluso las expresiones simples corren el riesgo de perder tanta precisión que el resultado puede ser inútil.

Los números positivos de 32 bits tienen una precisión decimal variable, que oscila entre 8,2 y 8,5 órdenes decimales para números con un valor absoluto de aproximadamente 1. Al calcular X, nos dan una respuesta de 302.882 31 , que tiene el doble de dígitos significativos. Además, no olvide que los números positivos de 32 bits tienen un rango dinámico de más de 144 decimales, y los flotantes de 32 bits tienen un rango dinámico mucho más pequeño de 83 bits. Por lo tanto, la precisión adicional del resultado no se logra al reducir el rango dinámico.

4.5.2 Prueba cuádruple: problema del triángulo delgado de Goldberg

Hay un problema clásico de "triángulo delgado" [1]: encuentre el área de un triángulo con lados a , b , c cuando dos de los lados byc son solo 3 unidades del dígito menos significativo (Unidades en el último lugar, ULP) más largas que la mitad del largo lados (Fig. 17).


Fig. 17. El problema del triángulo delgado de Goldberg

La fórmula clásica para el área A usa la variable intermedia s:

$$

$$s = \ frac {a + b + c} 2; A = \ sqrt {s (s-a) (s-b) (s-c)}$$

El peligro en esta fórmula es que s está muy cerca del valor de a , y el cálculo $$$(s-a)$ aumenta mucho el error de redondeo. Probemos números flotantes IEEE de 128 bits (con precisión cuatro veces) para los cuales $$$a = 7, b = c = 7/2 + 3 \ por 2 ^ {- 111}$ . (Si toma el año luz como la unidad de medida, el lado corto será la mitad del lado largo solo 1/200 del diámetro del protón. Pero esto hace que un triángulo sea la altura de la puerta en la parte superior). También calculamos el valor de A usando números positivos de 128 bits ( es = 7). Los siguientes son los resultados:

$$$$ display $$ \ begin {matrix} \ textrm {Valor verdadero:} & 3.14784204874900425235885265494550774498 \ dots \ times 10 ^ {- 16} \\ \ textrm {flotante IEEE de 128 bits:} & 3. \ color {orange} { 63481490842332134725920516158057682788} \ dots \ times 10 ^ {- 16} \\ \ textrm {128-bit posit:} & 3.147842048749004252358852654945507744 \ color {orange} {39} \ dots \ times 10 ^ {- 16} \ end {matrix} $$ mostrar $$

Los números de posición tienen hasta 1,8 dígitos decimales de precisión mayor que la flotación de precisión cuádruple en un amplio rango dinámico: desde $$$2 \ por 10 ^ {- 270}$ antes $$$5 \ por 10 ^ {- 269}$ . Esto es suficiente para evitar las consecuencias catastróficas de aumentar el error en este caso particular. También es interesante observar que la respuesta en formato positivo será más precisa que en formato flotante, incluso si al final la convertimos en positivo de 16 bits.

4.5.3. La solución de la ecuación cuadrática.

Hay un truco clásico diseñado para evitar errores de redondeo al calcular raíces $$$r_1$ , $$$r_2$ ecuaciones $$$ax ^ 2 + bx + c = 0$ usando la fórmula habitual $$$r_1, r_2 = (- b \ pm \ sqrt {b ^ 2-4ac}) / (2a)$ cuando b es mucho más grande que ayc , lo que lleva a la desaparición de dígitos a la izquierda, ya que $$$\ sqrt {b ^ 2-4ac}$ muy cerca de b . Pero en lugar de obligar a los programadores a recordar trucos místicos, podría ser mejor para hacer el cálculo seguro utilizando una fórmula simple de un tutorial. Poner $$$a = 3, b = 100, c = 2$ y compare el resultado en el formato de 32 bits flotante y positivo.

Tabla 5. La solución de la ecuación cuadrática


Raíz numéricamente inestable $$$r_1$ , pero tenga en cuenta que el positivo de 32 bits proporciona 6 dígitos correctos en lugar de 4 para flotante.

4.6. Comparación de flotadores y sistemas Posit para la prueba LINPACK clásica

Durante mucho tiempo, el método principal para evaluar las supercomputadoras fue resolver $$$n \ veces n$ sistemas de ecuaciones lineales $$$\ mathbf Ax = b$ . A saber, la prueba llena la matriz A con números pseudoaleatorios del 0 al 1, y el vector b con las sumas de las filas A. Esto significa que la solución x es un vector que consiste en unidades. La prueba calcula la tasa de deducción $$$\ | \ mathbf Ax-b \ |$ para verificar la corrección, aunque no hay un número fijo de dígitos que deben ser verdaderos en la respuesta. Una pérdida típica de varios dígitos de precisión es típica para la prueba, y generalmente se usan flotadores de 64 bits (no necesariamente IEEE). Inicialmente, la prueba proporcionó n = 100, pero este tamaño era demasiado pequeño para las supercomputadoras más rápidas, por lo que n se aumentó a 300, luego a 1000, y finalmente (del primer autor), la prueba se hizo escalable y proporciona el número de operaciones por segundo, basado en el hecho de que la prueba se realiza $$$\ frac {2} {3} n ^ 3 + 2n ^ 2$ operaciones de multiplicación y suma.

Comparando posit y float, notamos un pequeño inconveniente de la prueba: la respuesta en el caso general no es una secuencia de unidades, debido a errores de redondeo en las sumas en líneas. Tal error puede eliminarse si descubrimos cómo las ocurrencias en A contribuyen con 1 bit, que está fuera del rango de precisión posible, y establecemos este bit en 0. Esto nos dará la confianza de que la suma de la línea A es representable sin redondear, y que la respuesta es x es en realidad un vector que consiste en unidades. Para la versión original de la tarea, con un tamaño de 100x100, el flotador IEEE de 64 bits da una respuesta de este tipo:

0.9999999999999 633626401873698341660201549530029296875
1.00000000000000 11102230246251565404236316680908203125
$$$\ vdots$
1.0000000000000 22648549702353193424642086029052734375

Ninguno de los 100 números es verdadero; están cerca de 1 pero nunca son iguales a 1. Con los números positivos, podemos hacer algo maravilloso. Usando números positivos de 32 bits y el mismo algoritmo, calculamos el residuo $$$r = \ mathbf Ax - b$ El uso de la operación de fusión es un producto escalar. Entonces decide $$$\ mathbf Ax '= r$ (usando ya procesado $$$\ mathbf A$ ) y usar $$$x '$ para corrección: $$$x \ leftarrow x-x '$ . El resultado es la respuesta precisa sin precedentes para la prueba LINPACK: $$$\ {1, 1, ..., 1 \}$ .¿Pueden las reglas de LINPACK prohibir el uso de un nuevo tipo de números de 32 bits, cuyo uso permite lograr un resultado perfecto con un error cero, o continuar insistiendo en el uso de un flotante de 64 bits, que no lo permite? Esta decisión la tomarán los responsables de esta prueba. Para aquellos que necesitan resolver sistemas de ecuaciones lineales para resolver problemas reales, en lugar de comparar la velocidad de las supercomputadoras, posit ofrece ventajas sorprendentes.

5. Conclusión

Posit derrota el flotador en su propio juego: con él, puedes realizar cálculos y reducir los errores de redondeo. Los números de posición tienen mayor precisión, mayor rango dinámico y mayor cobertura. Se pueden usar para obtener mejores resultados que un flotador de la misma profundidad de bits, o (que puede ser una ventaja competitiva aún mayor), los mismos resultados con una profundidad de bits más baja. Dado que el ancho de banda del sistema es limitado, el uso de operandos más pequeños significa una velocidad más rápida y un menor consumo de energía.
Como funcionan como un flotador, y no como un sistema de intervalos, pueden considerarse como un reemplazo directo del flotador, como se demostró aquí. Si el algoritmo que usa float pasa las pruebas, y el tiempo y la estabilidad son "suficientemente buenos", funcionará aún mejor con posit. Las operaciones fusionadas disponibles en positivo proporcionan una herramienta poderosa para evitar la acumulación de errores de redondeo y, en algunos casos, le permiten usar de forma segura números positivos de 32 bits en lugar de flotantes de 64 bits en aplicaciones que requieren un alto rendimiento. En general, esto aumentará el rendimiento de la aplicación de 2 a 4 veces y reducirá el consumo de energía, ahorrará energía y reducirá el costo de almacenamiento de datos. El soporte de hardware positivo nos dará el equivalente de uno o dos pasos de la Ley de Moore,sin la necesidad de reducir el tamaño del transistor o aumentar el costo. A diferencia del flotante, el sistema de posit ofrece reproducibilidad bit a bit de resultados en diferentes sistemas, eliminando el principal inconveniente del estándar IEEE 754. Los números de posit son más simples y elegantes que el flotante, y reducen la cantidad de equipo para soportarlos. Aunque los números flotantes ahora son ubicuos, los números positivos pronto pueden volverlos obsoletos.

Referencias

1. David Goldberg. Lo que todo informático debería saber sobre la aritmética de coma flotante.
ACM Computing Surveys (CSUR), 23 (1): 5–48, 1991. DOI: doi: 10.1145 / 103162.103163.
2. John L Gustafson. El fin del error: Unum Computing, volumen 24. CRC Press, 2015.
3. John L Gustafson. Más allá del punto flotante: aritmética informática de próxima generación. Seminario de Stanford: https://www.youtube.com/watch?v=aP0Y1uAA-2Y , 2016. Transcripción completa
disponible en http://www.johngustafson.net/pdfs/DebateTranscription.pdf .
4. John L Gustafson. Un enfoque radical para el cálculo con números reales. Supercomputing
Frontiers and Innovations, 3 (2): 38–53, 2016. doi: http://dx.doi.org/10.14529/jsfi160203.
5. John L Gustafson. El gran debate @ ARITH23. https://www.youtube.com/watch?v=
KEAKYDyUua4 , 2016. Transcripción completa disponible en http://www.johngustafson.net/pdfs/
DebateTranscription.pdf .
6. Ulrich W Kulisch y Willard L Miranker. Un nuevo enfoque para la computación científica, volumen 7. Elsevier, 2014.
7. Más sitios. Estándar IEEE para aritmética de punto flotante. IEEE Computer Society, 2008.
DOI: 10.1109 / IEEESTD.2008.4610935.
8. Isaac Yonemoto. https://github.com/interplanetary-robot/SigmoidNumbers