Dio la casualidad de que la ciencia se está desarrollando de manera desigual y, por lo tanto, en nuestra vida actual, por así decirlo, hay un lugar para el logro. Una hazaña, por supuesto, científica, pero de esto no menos importante. Y ahora, lectores, tienen la oportunidad de ver el lugar de la hazaña, los precios oficiales de su pago (como es habitual en países que se autodenominan civilizados) e incluso probar suerte usted mismo. Bueno, al mismo tiempo, al menos algunos de ustedes sentirán el encanto de encontrar perlas en cosas bastante comunes.
Además, en varias series, se seguirá una historia sobre las cosas que son accesibles para cualquier graduado de la escuela secundaria (e incluso para muchos niños en edad escolar). No habrá evidencia, ya que a menudo son obvias, y si se presentan aquí no solo ampliarían el volumen, sino que también asustarían a muchos lectores.
Primera serie
Primero hubo estrellas. Hubo un proceso de jugar con ellos, mirarlos y sentirlos, vomitar y observar un brillante sendero de caída. Las estrellas eran patrones. Y los números eran el cajón de arena. Los números cambiaron al nuevo lado, y otra estrella apareció en los espacios entre ellos. Su resplandor hizo señas y, lo mejor de todo, no se quemó, pero permitió que la tocaran, la levantaran y luego los saludó con la mano para dejar un rastro brillante de polvo de estrellas. Pero luego las estrellas se familiarizaron y quedaba un trabajo para clasificarlas. Y entonces surgió una idea.
La idea era simple: puedes ganar dinero con ella. Y sí, realmente motivado. Pero no creció juntos. Fue entretenido, había estrellas regulares que brillaban de una manera nueva, había placer y progresos. Solo al final surgió un bosque, un bosque continuo de árboles brillantes. Y era débil, no podía clasificar esta taiga en busca de la luz verdadera, porque hay millones de árboles y estoy solo. Por lo tanto, le sugiero que mire las estrellas, y si son interesantes, entonces puede ganar $ 400K, pero la verdad es que hay un "pero": en el bosque debe poder elegir el camino correcto.
En los acercamientos a las estrellas
¿Qué es un número? Por un lado, es un producto de nuestra mente sombría, que no se encuentra en la naturaleza. Pero, por otro lado, tal abstracción nos permite modelar muchos procesos que observamos todos en la misma naturaleza. Solo el modelo no es igual al fenómeno observado. Así que nuevamente estamos tratando con la adaptación a nuestras capacidades modestas de formas de describir la naturaleza. ¿Esto es bueno? En términos de precisión, la descripción no es muy buena. No porque alguien no tenga suficiente número de decimales, sino porque un fenómeno modelado incorrectamente puede sorprendernos enormemente cuando resulta que el modelo carece de una u otra característica específica que está presente en la realidad e incluso a veces puede sonar un poco molesto naturalistas desatentos en la cabeza.
A la luz de lo anterior, intentemos indagar sobre la integridad de la base de cualquier modelado: la integridad de la comprensión del concepto de número. Parece que solo un número, solo el conocimiento al respecto, establecido desde la primera infancia, bueno, ¿qué más podría ser? Pero justo allí podemos encontrar el abismo. Sí, el que no tiene fondo y está lleno de estrellas.
No hay números en la naturaleza. Pero en la naturaleza puedes ver la relación. La nube es más grande (más larga / más ancha / más gruesa / like_you_ else_will_be_becoming) que la otra nube, lo que significa que hay un lugar para la correlación. Pero la relación tampoco tiene números. Solo hay dos nubes, una más, la otra menos, y existe su relación. Aunque sí, la proporción también fue inventada por el hombre. Por lo tanto, uno puede preguntarse: ¿de qué sirve? El beneficio es este: el concepto de correlación está un paso por delante del concepto de número. Al principio había una relación, y solo entonces apareció un número. Más precisamente: números fraccionarios. Por lo tanto, entendiendo la relación, entenderemos los números.
¿Cómo se obtienen los números fraccionarios? Muy simple: desde la necesidad de modelar la correlación. Al principio había proporciones de escalones y lados de la tierra, ovejas de un dueño a ovejas de otro, el peso de una sandía al peso de otro. En todos estos casos, era necesario expresar de alguna manera la diferencia. Pero la diferencia no estaba dividida estrictamente por el número de pasos o por el tamaño de la sandía vecina. Al principio aprendieron a expresar la diferencia al dividirlos en unidades de medida más pequeñas (se añadieron codos a los escalones y se agregaron dedos a los codos). Pero la ciencia no se detuvo y exigió una precisión cada vez mayor. Como resultado, todos estuvieron de acuerdo en la uniformidad, olvidando los dedos, los codos, los pasos y otras libras con la libra esterlina. La uniformidad se expresa en número.
¿Cómo correlacionar dos segmentos si uno de ellos no encaja en el otro un número entero de veces? Puede medir con los dedos, pero será más preciso tomar un segmento más pequeño como unidad de medida y dividirlo en partes idénticas. Con estas partes, puede medir esa parte de un segmento más grande que no se mide por todo el segmento más pequeño. Pero luego surge una nueva parte del segmento más grande, que ya no es medible por las partes seleccionadas. Aplicamos la recursividad y nuevamente dividimos las partes ya rotas en componentes aún más pequeños. Los medimos previamente inconmensurables. Y de nuevo obtenemos un resto inconmensurable. Divide las partes nuevamente, mide nuevamente. Nuevamente tenemos el resto. ¡Pero puedes aburrirte!
Como resultado, a la gente se le ocurrió la idea de redondear y dejó de volver a dividir la unidad de medida. Es decir, las personas puntuaron en precisión (dicen que es suficiente). Pero la naturaleza no perdona las imprecisiones en el modelado.
¿Cómo se modelan las relaciones hoy? Se modelan utilizando la clasificación de números fraccionarios. La clasificación es la siguiente: hay números enteros y números fraccionarios. Los enteros aún son inestables, pero los fraccionarios se dividen en fracciones finitas e infinitas. Por el momento, también nos olvidamos de los finales. Los infinitos se dividen en racionales e irracionales. Por lo general, nos olvidamos de la primera parte. Los irracionales se dividen en algebraicos y trascendentales. Todo, no más divisiones. Pero para mayor claridad, damos una clasificación en forma de imagen:
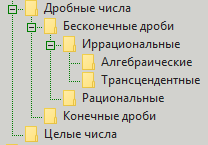
¿Por qué es mala esta clasificación? Ella no es tan mala. Ella, como solía decir Winnie the Pooh, es buena, pero por alguna razón coja ... Es decir, está claro que con la precisión de la expresión de valores, no todo está bien con ella debido al infinito. Pero hay otra cara de la moneda. Este lado (en este contexto) se llama "divisibilidad". No podemos separar con precisión dos números (uno sobre otro) porque descansamos contra el infinito. Pero, por otro lado, estamos interesados en fenómenos del mundo de los números como la simplicidad y el número de divisores que eliminan el infinito cuando aparecen. Los números primos forman la base de la serie numérica de enteros. Y estos números importantes (incluidos, por ejemplo, la comodidad cuando se paga de forma remota por los servicios) dependen mucho de la operación de la división. Y la división a menudo nos da fracciones. Y las fracciones nos dan números fraccionarios. Bueno, para los números fraccionarios, alguien nos dio la clasificación previamente dada de finito, infinito, racional, irracional, algebraico y trascendental. ¿Pero esta clasificación nos da la oportunidad de encontrar respuestas a preguntas sobre números? Por ejemplo, ¿sobre los mismos simples? O fraccional? Parece dar, pero no tanto como nos gustaría.
Toma números primos. Hoy, los primos máximos se están buscando esencialmente. Es decir, toman el número de candidato y luego verifican si es simple o no. Los candidatos obtienen números simplemente: si conoce el método de verificar la simplicidad para una determinada clase de números, aquí está la lista de candidatos en forma de representantes de la clase por la que pasan estúpidamente en una fila, verificando cada número, comenzando, por supuesto, con valores pequeños. Y hasta ahora han llegado a números del orden de dos hasta el grado de ochenta millones. Este es un número de casi veinticinco millones de decimales. En principio, se ve impresionante. Pero, ¿qué nos impide recordar el eslogan "más alto, más lejos, más rápido"?
Fundamentalmente, nos obstaculiza la falta de comprensión. Sí, nuestro modelo del fenómeno llamado "número" está incompleto. Y sí, la parte del modelo, llamada "división", está incompleta en su mayor grado. Por lo tanto, ochenta millones de unidades en la memoria de la computadora es el límite para la humanidad. ¿Por qué unidades? Porque parece que son los números primos más grandes. Estas son una unidades, pero en notación binaria. Para ellos, está la prueba de Luc-Lemer, que nos muestra un número simple o un compuesto. Y esta prueba requiere años de trabajo de un núcleo de procesador para verificar un número candidato de ochenta millones de unidades binarias. Solo ochenta megabytes, o diez megabytes, y la humanidad ya no puede dar un paso más. ¿Qué son diez megabytes? Esto es un centavo, esto es un poco, no es casi nada para las computadoras modernas. Pero la prueba ha estado sucediendo por años. Por lo tanto, debe ejecutarlo en millones de computadoras en las que los voluntarios instalan el programa apropiado y, como resultado, verificar un número de candidato durante un cierto número de segundos (y esto si hay muchos voluntarios). Pero el problema es que hay muchos números de candidatos y, por lo tanto, lleva muchos meses encontrar el próximo número primo. Y con tal deliberación, uno puede esperar que el movimiento de solo cientos de millones de unidades binarias llevará diez años.
¿Es posible acelerar el proceso? Usted puede Pero se necesita más comprensión. Por ejemplo, ¿cómo reducir el tiempo para probar cada número? Hasta ahora, tal disminución se logra masajeando hierro. O la segunda opción: puede ofrecer una prueba de simplicidad más rápida. Pero con esto durante unos 100 años, poco ha cambiado. Y, sin embargo, si lo resuelves, tal vez funcione con nosotros. Solo necesito entender desde lo más básico.
Estrellas cerca
Pensando en las relaciones, todos pueden contribuir mucho a la ciencia. Solo ser curioso es suficiente. Por ejemplo, uno puede preguntarse, ¿por qué la clasificación de números fraccionarios es tal? Y encuentre la respuesta en un experimento mental para medir la razón de los mismos segmentos. Primero, los segmentos están correlacionados como 1 a 2. Esta relación es comprensible, nos da el número 2, que muestra cuántas veces el segmento más grande excede al más pequeño. Y ahora alarguemos un segmento un poco más pequeño. Que va a pasar La relación dejará de ser completa. El exceso obtenido por el alargamiento nos impide obtener una respuesta simple en el problema. Pero podemos usarlo como regla. Si se ajusta un número entero de veces en medio segmento más grande, entonces podemos expresar la relación a través de este entero. Entonces obtenemos la proporción:
(1+1/N)/2
donde N es el número de veces que se necesita para ajustar el exceso al estirar la longitud más pequeña a la mitad de la longitud más grande. Entonces tenemos un número racional. Siempre está dada por la relación de enteros. Si ahora extendemos el segmento más pequeño un poco más, entonces podemos obtener una situación en la que no importa cuánto multipliquemos el segmento más pequeño por un número entero, no podemos obtener una coincidencia exacta con un cierto número de longitudes del segmento más grande. Entonces obtuvimos un número irracional que caracteriza la nueva relación. Tenga en cuenta que un desplazamiento microscópico del límite del segmento conduce a un proceso interminable de identificación de la relación de longitudes. Un paso para el humilde investigador y un gran cambio para la teoría de números: se requiere un nuevo elemento en la clasificación. Un paso y, desde el tamaño micro hasta el infinito. De una categoría de números a una completamente nueva, fundamentalmente incompatible con la anterior. ¿No es eso una estrella?
Pero, de hecho, solo cambiamos ligeramente un segmento. Entonces, ¿de dónde vino la categoría fundamentalmente nueva? En general, la clasificación es importante por su capacidad de coincidir exactamente con la realidad. Pero, ¿qué tipo de precisión vino junto con los números irracionales? Le permiten modelar cualquier proporción, y no solo la proporción de enteros, por lo que realmente tiene sentido separar tales clases. Pero esto no es todo precisión, porque quiero entender todos estos infinitos, cómo aparecen, qué significan y por qué existen. Es cierto, con infinitos, no todo es fácil, pero porque por ahora trataremos con relaciones finitas. Parece que todo es simple con ellos, toma N, divídelo por M y obtén un número fraccionario. Será muy bueno si el número resulta ser corto, por ejemplo 2.5 o 3.25. Pero con mayor frecuencia para el mundo hay relaciones de la forma 4.12 (3456), es decir, nuevamente con infinitos, pero estos son infinitos "en período". Solo notando los números repetidos, puede grabar de manera muy fácil y compacta un número de un número infinito de caracteres. Así es como nos enfrentamos al infinito. También un pequeño asterisco. Pero esto es solo una mirada superficial.
Ahora activemos la curiosidad y hagamos preguntas. ¿Y por qué algunos números fraccionarios son finitos y otros infinitos? ¿Y por qué algunos tipos de infinito son infinitamente largos, mientras que otros tienen un período? ¿Y por qué antes del período en el número 4.12 (3456) vemos los números 1 y 2? ¿Y por qué existe un preperíodo? ¿Y por qué en el período vemos los números 3 y 4? ¿Y por qué la duración del período en este ejemplo es igual a cuatro? ¿Y por qué el número de números antes del período es igual a dos? Y solo echamos una mirada curiosa superficialmente a solo un número fraccionario. Y para otros números, las preguntas serán aún más interesantes.
Tratemos de responder. ¿Por qué los números fraccionarios son finitos? Muy simple, de hecho, esta es una "ilusión óptica". Más precisamente: utilizamos un truco. Por ejemplo, para obtener el número 2.5, puede dividir 5 entre 2. Y para esto, todos en la escuela enseñamos el método de dividir la "esquina". Pero echemos un vistazo más de cerca a este método. Y luego encontramos que el fakir actúa de la siguiente manera: multiplica el dividendo por una constante que contiene el divisor, o sus factores. Y luego reduce exactamente los factores de la constante a los factores del divisor. Se ve así:
5/2=2+1/2=2+(1∗10/2)/10=2+1∗5/10=2.5
Eso es todo milagros: un deuce de un divisor se reduce a un deuce de una constante
10 que es igual a
5∗2 , y como resultado quedó un cinco, que se escribe después del separador decimal. El numero es
1 nunca compartido
2 , se multiplica por
0.5 de la cantidad
2+1∗0.5 . Pero no lo vemos, gracias a la misma "ilusión óptica" que entrenamos desde la escuela para crear de forma independiente durante cada operación de división de división. Bueno, ¿no es eso una estrella? Uno solo tenía que empujar el follaje sobre las representaciones apagadas desde la época de la escuela primaria, cuando vimos la luz de algo nuevo, no del todo ordinario, que no se enseña en la escuela (sino en vano).
Expliquemos ahora la "ilusión óptica" en un nivel ligeramente superior. Simplemente tradujimos el resultado de la división a un formato conveniente para el almacenamiento y la percepción. El número en sí no depende del formato. Y la cantidad de personajes que contiene también. Ya hemos visto la posibilidad de poner corchetes alrededor de un período, y así reducir el infinito a la duración del período y dos corchetes. Y este también es un formato de datos, pero se usa para fracciones periódicas. Y el formato de fracciones finitas oculta el infinito al reducir por factores desde la base del sistema de números decimales. Si tomamos, por ejemplo, el sistema de números ternarios, la división de 5 por 2 se verá así:
5/2=2+1/2=2+(1∗3/2)/3=2+(1+1/2)/3=2+(1+(1∗3/2)/3)/3=
= 2 + ( 1 + ( 1 + 1 / 2 ) / 3 ) / 3 = . . . = 2.1 ( 1 )
Es decir, obtuvimos infinito en forma de una fracción periódica, porque ahora usamos otra constante que no contiene factores que pueden reducirse con el número 2. Pero en un sistema hexadecimal el resultado volvería a ser definitivo: 2.3. Pero el número en sí permanece en algún lugar a la sombra, y probablemente el mejor registro sería 5/2, y todo lo demás es cuestión de elegir el formato de presentación para este número.
Ahora sobre fracciones infinitas. Los periódicos se obtienen dividiendo enteros, y los irracionales (con longitud de período infinita) se obtienen calculando una raíz de cierto grado a partir de un entero. Es decir, las personas derivaron dos categorías de división a partir de la abstracción de enteros, con factores diferentes y con los mismos. La primera opción le permite dividir cualquier número entero en cualquier otro número entero, pero a veces da un resultado fraccionario. La segunda opción le permite dividir los números solo en aquellos que son exactamente iguales al resultado de la división (incluyendo múltiples para raíces de grandes grados). En general, tenemos la misma división, pero sin limitación en el resultado y con la restricción. La restricción nos lleva a dos opciones: reducir el divisor con un factor del dividendo (y luego puede obtener un número entero igual al divisor), o dividir el dividendo irreducible por un número determinado. ¿Qué puede ser entonces un "cierto número"? Si es un número entero, entonces como resultado obtenemos una fracción (el dividendo y el divisor son irreductibles), que no es igual a un número entero. Por lo tanto, dado que los enteros no encajan, debe buscar una fracción que sea igual al resultado. Las fracciones finitas también desaparecen, porque en realidad representan un número de la forma
N / M que, cuando se multiplica por sí mismo, nos daría una nueva fracción de la forma
N ∗ N / ( M ∗ M ) , que nuevamente nos da una fracción finita o periódica, y no un número entero. Por lo tanto, es necesario seleccionar una fracción que reduzca la relación de sus cuadrados a un número entero con un crecimiento infinito de N y M. Por qué para enteros infinitos la razón
N ∗ N / ( M ∗ M ) se puede completar, pero no para el final? Porque cuantos más números, menos influencia sobre el resultado es su discreción. El número entero que sigue a cualquiera elegido es necesariamente diferente de uno por uno. Y esta unidad no le permite establecer con precisión el resultado deseado, porque, por ejemplo, entre 1/1000 y 2/1000 hay infinitos números, por ejemplo 11/10000 o 145/100000, etc. Por lo tanto, al aumentar la longitud del número, es posible en el infinito obtener cualquier resultado con precisión. Y luego multiplíquelo por sí mismo y obtenga un número entero.
Y al mismo tiempo, el período de tal fracción realmente se vuelve infinito, como veremos más adelante. Y un período infinito es propiedad de un número irracional, al que hemos pasado de números completamente racionales. Aquí hay una luz estelar que se convierte suavemente en la oscuridad del infinito.Pero, ¿por qué necesitamos esta unión entre dos clases de números? Tal vez uno es suficiente? Tratemos de simular. Así que obtuvimos exactamente la raíz de un número entero, encontramos dos números enteros grandes que tienden al infinito, que, al cuadrado y divididos entre sí, dan un número entero. Ahora agregue uno a cualquiera de estos números infinitamente grandes. ¿Qué pasará entonces? En nuestro lenguaje habitual, obtuvimos una definición para un nuevo número, que no es periódico (porque tiene un período infinito) y al mismo tiempo no es la raíz del todo. Es decir, el nuevo número no encaja en la clasificación que nos dan los números racionales e irracionales. Y ahora todos esos números fueron llamados por matemáticos trascendentales, porque hay que ponerlos en algún lugar. Pero un punto interesante: al principio había raíces de enteros, llamados números irracionales,y luego aparecieron "otros" números. Es decir, primero, en aras de la antigua tradición griega, la sobreestimación de la importancia de los enteros se clasificó precisamente sobre la base de los métodos de obtención de enteros. El primer método fue la división y los números racionales derivados de él. Entonces la gente se encontró con raíces. Entonces había números irracionales. Y además de lo racional y lo irracional, surgió una tercera categoría. Además, la tercera categoría al principio era una rareza terrible que Euler descubrió, pero además del descubrimiento de Euler simplemente no había otros así. Y se decidió dividir lo irracional en dos clases: algebraico (es decir, creciendo desde las raíces) y trascendental (especial, sobresaliente, yendo más allá, porque solo Euler podría encontrarlos). Pero más tarde, los números que no provenían de las raíces se volvieron masivos, y los matemáticos incluso determinaron que había muchos más,que algebraico Por lo tanto, la trascendencia (característica) de tales números se ha convertido solo en un tributo a la tradición. Aunque si recordamos el concepto de correlación, entonces todos estos racionales, irracionales, algebraicos y trascendentales se convierten inmediatamente en nombres artificiales para una división muy condicional de números que resulta de un cambio simple del final de uno de los segmentos comparados. Bueno, con tal enfoque, los números trascendentales se convierten simplemente en "el resto", es decir, si por la relación de segmentos, en aras de mantener la tradición de extraer enteros, seleccionamos las clases obtenidas por las operaciones de dividir y extraer la raíz de los enteros, obtenemos solo racional y algebraico, pero todos El resto son trascendentales. Es decir, en total solo hay tres categorías de fracciones infinitas. Por lo tanto, el nombre "trascendental" se vuelve algo tenso,no lo encuentras Bueno, está bien, porque la tradición es nuestro todo, incluso en una ciencia tan exacta como las matemáticas.Eso es todo por ahora. En la próxima serie, hablemos de estrellas racionales.