Cómo colorear los polinomios correctamente

Los polinomios no son solo ejercicios en materias abstractas. Son excelentes para detectar estructuras en lugares inesperados.

En 2015, un ex poeta que se convirtió en matemático, Jun Ho ayudó a resolver el problema formulado hace unos 50 años. Se asoció con objetos matemáticos complejos, " matroides " y gráficos (combinaciones de puntos y segmentos). Y también estaba relacionado con polinomios, expresiones que nos son familiares de las lecciones de matemáticas, que consisten en la suma de variables planteadas en varios grados.

En algún momento de la escuela, probablemente pasaste por la apertura de corchetes en polinomios. Por ejemplo, puede recordar que x ² + 2xy + y ² = (x + y) ² . Un truco algebraico conveniente, pero ¿dónde puede ser útil? Resulta que los polinomios ayudan perfectamente a revelar estructuras ocultas, y Ho utilizó activamente este hecho en su prueba. Aquí hay un acertijo simple que ilustra esto.

Supongamos que necesitamos sentar dos equipos de jugadores en una mesa cuadrada. Para evitar el fraude, debe asegurarse de que los jugadores no se sienten junto a otros jugadores de su equipo. ¿Cuántos métodos de asiento hay?

Comencemos con los asientos del equipo rojo y azul. Digamos que el jugador rojo se encuentra en la parte superior de la tabla:



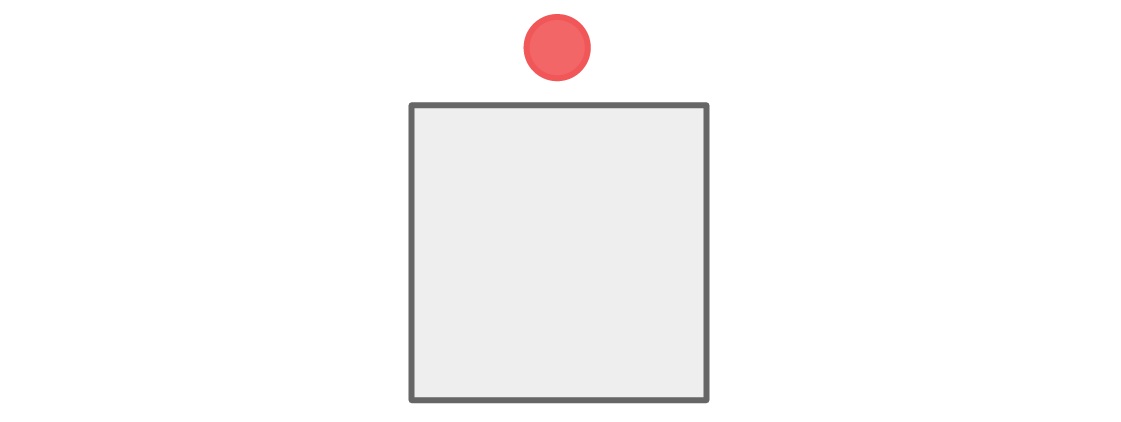
Hay dos lugares cerca del lugar superior, derecho e izquierdo, y para cumplir la regla, estos lugares deben ser ocupados por jugadores azules.



El espacio de abajo es adyacente a los dos azules, por lo que el jugador rojo debe sentarse allí.



Ninguno de los jugadores está sentado junto a un miembro de su equipo, y nuestra condición se cumple.

También podríamos comenzar con el jugador azul en la parte superior. Consideraciones similares conducen a la siguiente disposición:



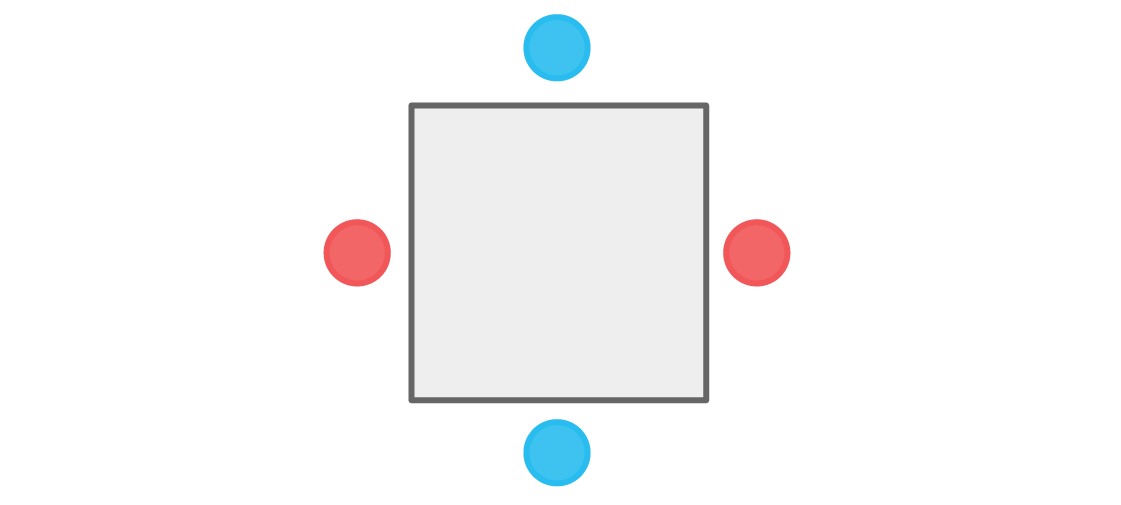
De nuevo, ningún jugador se sienta junto a otros miembros de su equipo. Nuestra condición se cumple, y tal disposición de asientos es aceptable. De hecho, hay exactamente dos de esos arreglos de asientos. Tan pronto como elegimos el color del punto superior, todo el resto está completamente definido.

Hay una manera de descubrir que solo hay dos posibles arreglos de asientos sin dibujar todos estos diagramas. Comencemos desde arriba: tenemos dos opciones, rojo y azul. Después de esta elección, queda una opción (un color diferente) para los asientos izquierdo y derecho. Y para el asiento inferior solo queda una opción: el color con el que comenzamos. Usando el "principio fundamental de cálculo", sabemos que el número total de oportunidades es el resultado de multiplicar el número de oportunidades para cada una de las opciones. Esto nos da 2 × 1 × 1 × 1 = 2 plántulas, como determinamos a partir de nuestros diagramas.

Ahora agregue el tercer comando con el tercer color. Imagina que tenemos jugadores rojos, azules y amarillos. ¿Cuántos asientos se pueden hacer, siempre que los lugares vecinos sean de diferentes colores? Para obtener una imagen de todas las posibilidades, tendrá que dibujar un vagón completo de diagramas, así que intentemos hacer cálculos.

Para el primer puesto, ahora tenemos una opción de tres colores. Después de esta elección, podemos elegir cualquiera de los dos colores restantes para los lugares izquierdo y derecho.

¿Qué habrá debajo del cuadrado? Existe la tentación de declarar que para el último asiento solo habrá una opción, ya que está al lado de los asientos izquierdo y derecho. ¿Pero te sientes defectuoso en esta lógica?



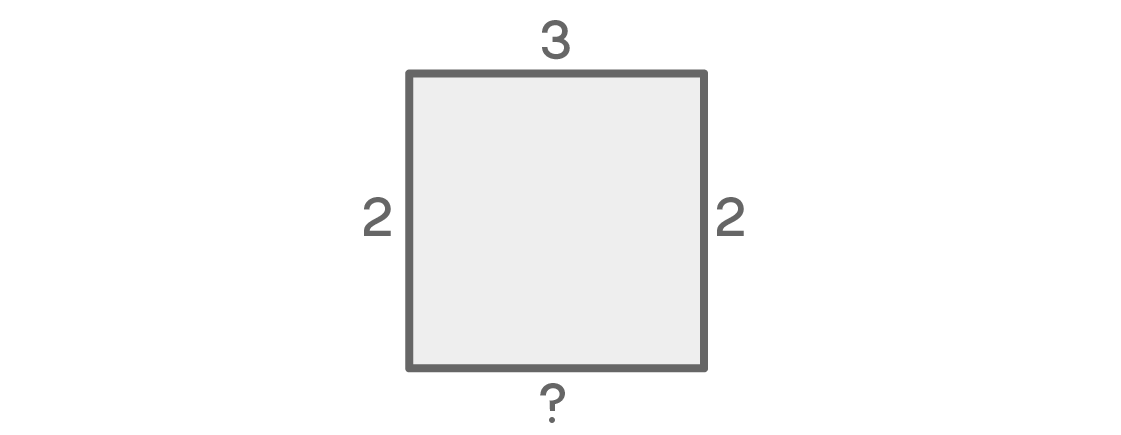
De hecho, si los lugares izquierdo y derecho tienen colores diferentes, entonces para el lugar inferior solo habrá una opción. Si a la izquierda, por ejemplo, es azul y a la derecha es rojo, entonces la parte inferior debe ser amarilla. Pero, ¿qué pasa si los colores izquierdo y derecho son iguales? En este caso, para el lugar inferior habrá una opción de dos opciones. Esta última opción depende de las anteriores, lo que complica nuestros cálculos.

Tenemos que considerar dos casos diferentes: cuando los colores de la izquierda y de la derecha coinciden, y cuando difieren.

Si los colores de la izquierda y de la derecha coinciden, el número de posibilidades para cada uno de los lugares es el siguiente:



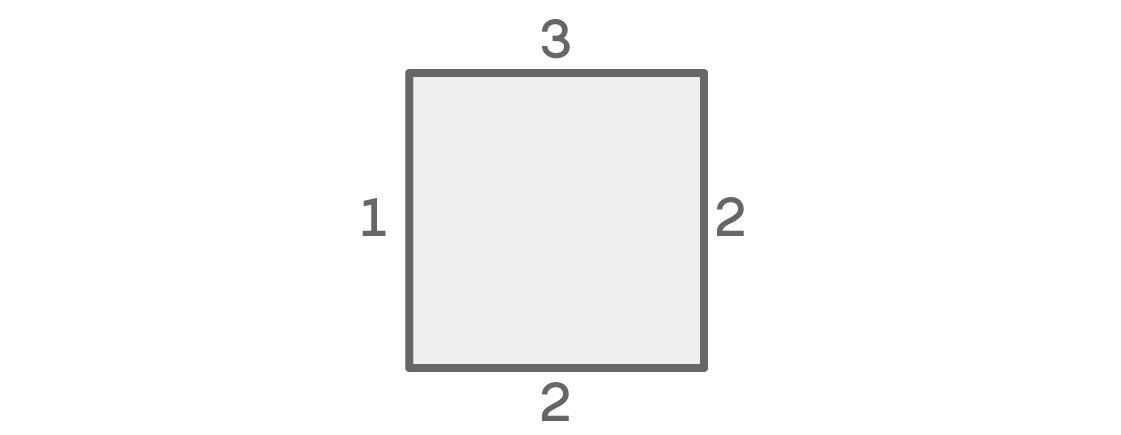
Para el asiento superior, tenemos tres opciones. Quedan dos a la derecha. Como suponemos que los lugares izquierdo y derecho tienen el mismo color, solo tenemos una opción para el lugar izquierdo: el mismo color que el derecho. Finalmente, dado que el color es el mismo a la izquierda y a la derecha, podemos elegir cualquiera de los dos colores restantes para el asiento inferior. Como resultado, obtenemos 3 × 2 × 1 × 2 = 12 posibles arreglos de asientos.

Ahora veamos esas posibilidades cuando los colores de la derecha y la izquierda son diferentes:



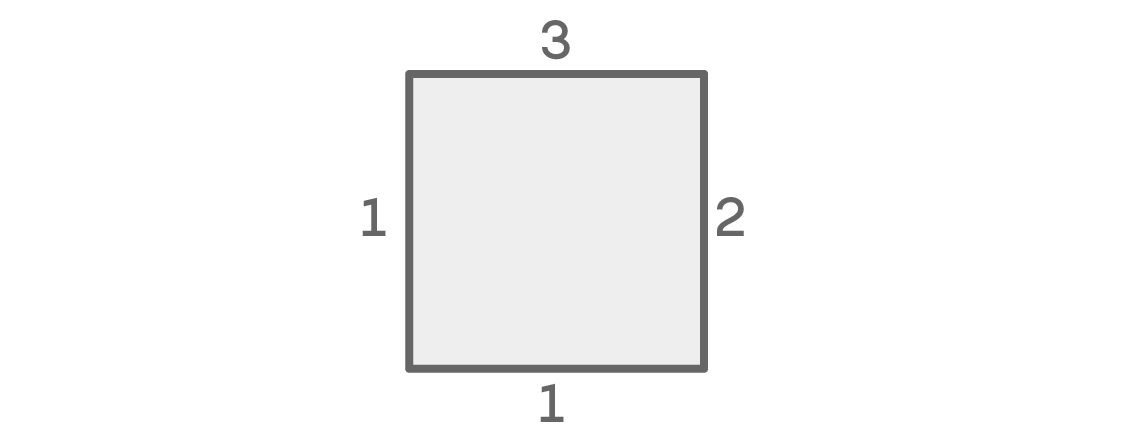
Nuevamente tenemos tres opciones para la parte superior y dos para el lugar correcto. El lugar izquierdo nuevamente tiene una opción, pero por una razón diferente: no puede ser lo mismo que la parte superior, vecina, y no puede ser lo mismo que la derecha, de acuerdo con nuestra condición. Y, dado que los colores de la derecha y la izquierda son diferentes, solo queda una opción para el lugar inferior (igual que la parte superior). Este caso da 3 × 2 × 1 × 1 = 6 posibles arreglos.

Dado que estas dos opciones cubren todas las posibilidades, las sumamos y obtenemos 12 + 6 = 18 posibles arreglos de asientos.

Agregar un tercer color complica nuestra tarea, pero nuestro trabajo duro será recompensado. Ahora podemos usar esta estrategia para 4, 5 o cualquier número q de diferentes colores.

Independientemente del número de colores, siempre tendremos dos casos: el izquierdo y el derecho serán del mismo color o de colores diferentes. Supongamos que tenemos una opción de q colores. Aquí hay una tabla que muestra el número de opciones para cada lado, en el caso en que los colores derecho e izquierdo son los mismos:



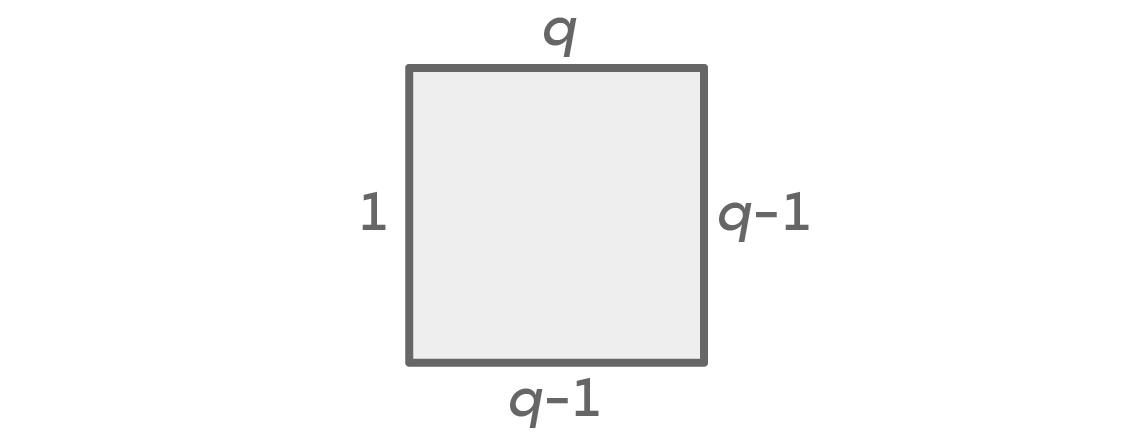
Primero tenemos q colores para el asiento superior y q-1 para el derecho. Dado que asumimos que los colores de la izquierda y la derecha son los mismos, solo tenemos una opción para el color izquierdo. Esto deja opciones q-1 para el punto inferior, porque puede ser de cualquier color que no sea el que elegimos para los puntos izquierdo y derecho. El principio fundamental de cálculo nos da q × (q - 1) × 1 × (q - 1) = q (q - 1) ² diseños posibles.

Si los lugares izquierdo y derecho tienen un color diferente, entonces podemos calcular las posibilidades de esta manera:



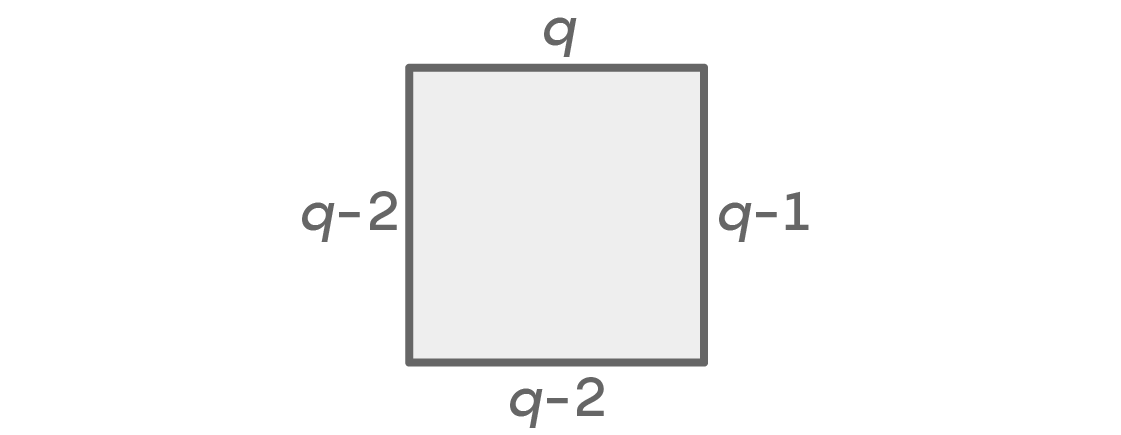
Una vez más, tenemos q opciones para la parte superior y q-1 para los lugares correctos. No puede haber el mismo color a la izquierda seleccionado para los lugares superior y derecho, por lo que hay opciones q-2. Puede haber cualquier color a continuación, excepto los dos que usamos a la izquierda y a la derecha, lo que nuevamente ofrece opciones de q-2. Obtenemos la suma q × (q - 1) × (q - 2) × (q - 2) = q (q - 1) (q - 2) ² posibles arreglos de asientos. Como estas dos situaciones cubren todas las opciones, nosotros, como antes, las sumamos y obtenemos el número total de arreglos posibles: q (q - 1) ² + q (q - 1) (q - 2) ² .

Tal expresión puede parecer una respuesta extraña a la pregunta: "¿Cuántos arreglos de asientos diferentes para diferentes equipos en la mesa cuadrada, de modo que dos miembros del mismo equipo no se sienten uno al lado del otro?" Sin embargo, este polinomio contiene mucha información sobre nuestro problema. No solo nos da una respuesta cuantitativa, sino que también revela la estructura de nuestra tarea.

Tal polinomio se llama el " polinomio cromático " porque responde a la pregunta: ¿cuántos métodos existen para colorear los vértices de una red (o gráfico) de modo que cualquier par de vértices vecinos tenga diferentes colores?

Inicialmente, nuestro problema estaba relacionado con los asientos alrededor de la mesa, pero podemos convertirlo fácilmente en una pregunta sobre cómo colorear los vértices del gráfico. En lugar de personas en la mesa:



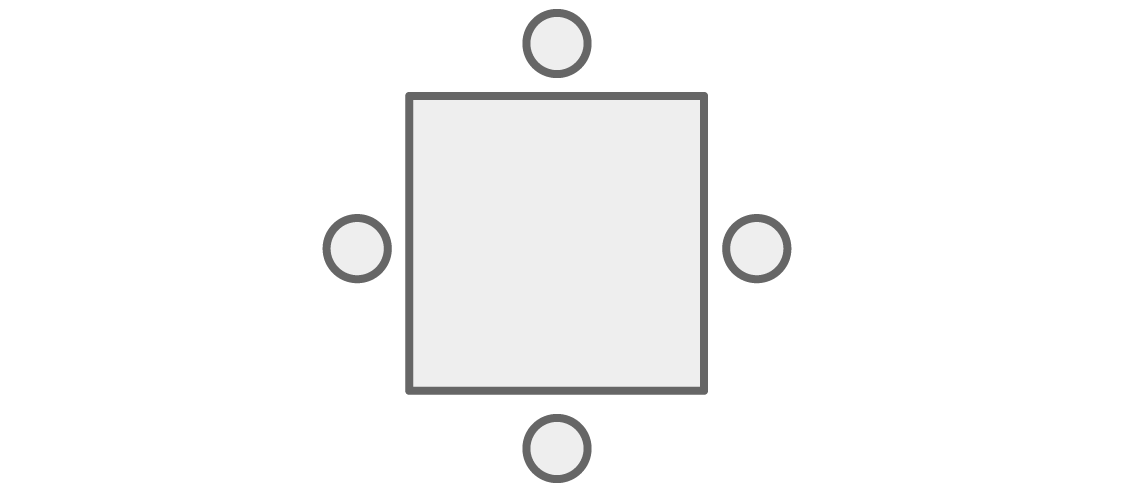
los imaginaremos en forma de picos conectados por bordes en el caso cuando estén sentados al lado de:



Ahora, cualquier coloración de los vértices del gráfico se puede representar como el asiento de las personas alrededor del cuadrado, donde "sentarse al lado" en la mesa significa "tener un borde común" en el gráfico.

Ahora, habiendo reformulado nuestro problema en forma de gráfico, volvemos al polinomio cromático. Lo llamamos P (q).

P (q) = q (q - 1) ² + q (q - 1) (q - 2) ²

Una propiedad notable de este polinomio es que responde a la pregunta de color para cualquier número posible de colores. Por ejemplo, para responder una pregunta con tres colores, ponemos q = 3 y obtenemos:

P (3) = 3 (3 - 1) ² + 3 (3 - 1) (3 - 2) ² = 3 × 2 ² + 3 × 2 × 1 ² = 12 + 6 = 18

Esta es la respuesta que recibimos en el caso de tres equipos. Y si ponemos q = 2:

P (2) = 2 (2 - 1) ² + 2 (2 - 1) (2 - 2) ² = 2 × 1 ² + 2 × 1 × 0 ² = 2 + 0 = 2

¿Te suena familiar? Esta es la respuesta a nuestro primer acertijo, con dos equipos. Podemos encontrar respuestas para cuatro, cinco o incluso 10 equipos diferentes, simplemente sustituyendo el valor deseado por q: P (4) = 84, P (5) = 260 y P (10) = 6 570. El polinomio cromático captó alguna estructura fundamental del problema resumiendo nuestra estrategia de conteo.

Podemos revelar más detalles de la estructura realizando operaciones algebraicas en nuestro polinomio P (q) = q (q - 1) ² + q (q - 1) (q - 2) ² :

= q (q - 1) (q - 1) + q (q - 1) (q - 2) ²
= q (q - 1) ((q - 1) + (q - 2) ² )
= q (q - 1) (q - 1 + q ² −4q + 4)
= q (q - 1) (q ² −3q + 3)

Extrajimos el factor q (q - 1) de cada parte de la suma y combinamos términos similares, reduciendo el polinomio a una forma factorizada. Y de esta forma, el polinomio puede informarnos sobre la estructura con la ayuda de sus "raíces".

Las raíces de un polinomio son valores de entrada en los que se vuelve igual a cero en la salida. Es más fácil encontrar las raíces en la forma factorizada: dado que el polinomio se expresa como partes multiplicadas, cualquier valor en el que uno de los factores sea igual a cero restablece todo el producto.

Por ejemplo, nuestro polinomio P (q) = q (q - 1) (q ² - 3q + 3) tiene un factor (q - 1). Si tomamos q = 1, este factor se vuelve igual a cero, como todo el resultado de la multiplicación. Es decir, P (1) = 1 (1 - 1) (1 ² - 3 × 1 + 3) = 1 × 0 × 1 = 0. Del mismo modo, P (0) = 0 × (–1) × 3 = 0 Por lo tanto, q = 1 y q = 0 son las raíces de nuestro polinomio. (Puede interesarle el factor (q ² - 3q + 3). Dado que no es igual a cero para cualquier q real, no da nuevas raíces a nuestro polinomio cromático).

Estas raíces tienen sentido dentro del marco de nuestro gráfico. Si tenemos una opción del mismo color, cada vértice debe ser del mismo color. No es posible colorear el gráfico para que todos los vértices adyacentes tengan colores diferentes. Esto es precisamente lo que significa que q = 1 es la raíz de nuestro polinomio cromático. Si P (1) = 0, entonces hay exactamente cero formas de colorear el gráfico para que los vértices vecinos no sean del mismo color. Lo mismo es cierto para la versión con número cero de colores, P (0) = 0. Las raíces de nuestro polinomio cromático nos informan sobre la estructura de nuestro gráfico.

La capacidad de ver la estructura a través del álgebra se vuelve aún más obvia si consideramos otros gráficos. Veamos un gráfico triangular:



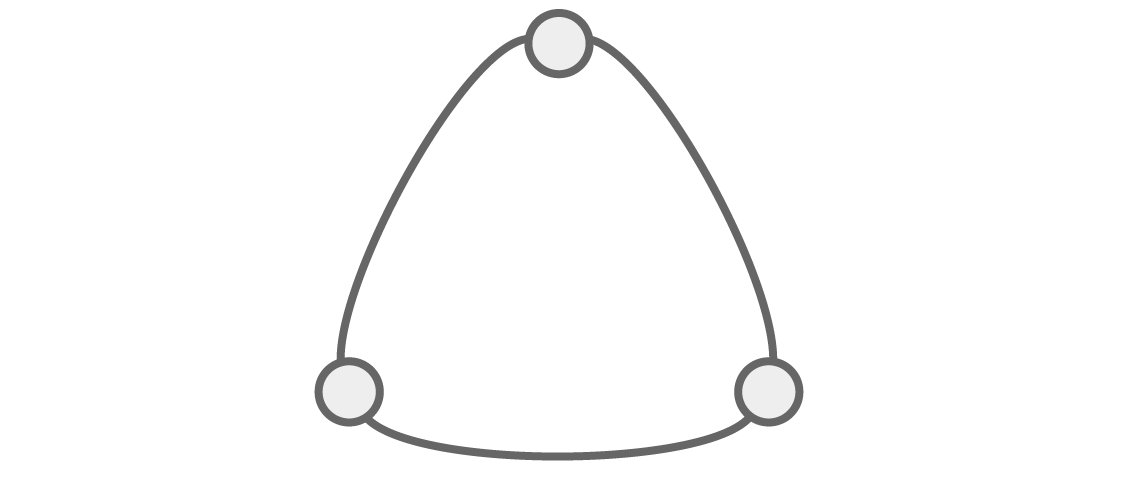
¿Cuántas maneras hay de colorear este gráfico q con colores para que los vértices vecinos no sean del mismo color?

Como de costumbre, para los primeros dos vértices vecinos hay opciones q y q-1. Y dado que el último vértice es adyacente a los dos primeros, debe diferir en color de ambos, lo que nos deja con opciones q-2. Esto nos da el polinomio cromático para este gráfico triangular: P (q) = q (q - 1) (q - 2).

En esta forma de factorización, este polinomio cromático nos dice algo interesante: tiene una raíz q = 2. Y si P (2) = 0, debería ser imposible colorear este gráfico con dos colores para que no tenga dos vértices adyacentes del mismo color. Es asi?

Imagine que estamos caminando en un círculo en este triángulo, coloreando los picos en el camino. Si solo tenemos dos colores, debemos alternarlos después de cada vértice: si el primero es rojo, el segundo será azul, lo que significa que el tercero debería volver a ser rojo. Pero los picos primero y tercero son adyacentes, y no pueden ser rojos ambos. Dos colores no son suficientes, como predijo el polinomio.

Usando un argumento alternativo similar, podemos llegar a una generalización significativa: el polinomio cromático de cualquier bucle cerrado con un número impar de vértices debe tener una raíz igual a 2. Dado que si alterna dos colores y se mueve a lo largo de un bucle de longitud impar, el primer y el último vértice coloreado serán del mismo color . Pero así como esto es un bucle, serán adyacentes. Colorear no es posible.

Por ejemplo, podemos usar varias técnicas para determinar que para un bucle con cinco vértices el polinomio cromático se ve así: P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q. Factorizando esto, obtenemos P (q) = q (q - 1) (q - 2) (q2 - 2q + 2). Como se esperaba, resulta que q = 2 es la raíz, y P (2) = 0. Curiosamente, tan pronto como encontramos esta conexión entre los gráficos y sus polinomios, las ideas comienzan a funcionar en ambas direcciones. Los polinomios nos pueden dar información sobre la estructura de los gráficos, y los gráficos nos pueden decir sobre la estructura de los polinomios.

Fue la búsqueda de la estructura lo que llevó a June Ho a probar la hipótesis de 40 años de Reed con respecto a los polinomios cromáticos. La hipótesis establece que si enumeramos los coeficientes del polinomio cromático en orden, ignorando sus signos, se cumplirá la siguiente condición: el cuadrado de cualquier coeficiente debe ser al menos el producto de dos vecinos. Por ejemplo, en el polinomio cromático para nuestro bucle de cinco vértices, P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q, vemos que 5 ² ≥ 1 × 10, 10 ² ≥ 5 × 10 y 10 ² ≥ 10 × 4. De esto, por ejemplo, se deduce que no todos los polinomios pueden ser cromáticos: los polinomios cromáticos asociados con gráficos tienen una estructura más profunda. Además, la conexión entre estos polinomios y otros dominios permitió a Ho y sus coautores responder una pregunta mucho más amplia relacionada con la hipótesis de Roth, varios años después de la prueba de la hipótesis de Reed.

Quizás los polinomios son mejor conocidos por su peor forma, como ejercicios abstractos en la manipulación formal de expresiones algebraicas. Pero los polinomios y sus propiedades (raíces, coeficientes, diversas formas) ayudan a revelar estructuras en lugares inesperados, creando conexiones con el álgebra en todo lo que nos rodea.

Ejercicios

1. Un gráfico completo es un gráfico, cada par de vértices está conectado por un borde. Encuentra el polinomio cromático de una gráfica completa de cinco vértices.


2. Encuentre el polinomio cromático para el siguiente gráfico (use información sobre los polinomios cromáticos de gráficos más simples).




3. Un gráfico se llama de dos lados si sus vértices se pueden dividir en dos grupos, A y B, de modo que los vértices de A sean adyacentes solo a los vértices B, y los vértices B sean adyacentes solo a los vértices de A. Suponga que el gráfico G tiene un polinomio cromático P (q) ¿Qué propiedad P (q) le permite concluir que la gráfica G tiene dos lados?