Hay muchos artículos en Internet con una descripción del algoritmo de descenso de gradiente. Habrá otro.

El 8 de julio de 1958, The New York Times escribió : “Un psicólogo muestra el embrión de una computadora diseñada para leer y ser más sabia. Desarrollado por la Armada ... la computadora 704, que costó $ 2 millones, aprendió a distinguir entre izquierda y derecha después de cincuenta intentos ... Según la Armada, usan este principio para construir la primera máquina de pensamiento de la clase Perceptron, que puede leer y escribir; El desarrollo está planeado para completarse en un año, con un costo total de $ 100,000 ... Los científicos predicen que los Perceptrones posteriores podrán reconocer a las personas y llamarlas por su nombre, traducir instantáneamente el habla oral y escrita de un idioma a otro. Rosenblatt dijo que, en principio, es posible construir "cerebros" que puedan reproducirse en la línea de ensamblaje y que sean conscientes de su propia existencia "(citado y traducido del libro por S. Nikolenko," Aprendizaje profundo, inmersión en el mundo de las redes neuronales ").

Ah, estos periodistas saben cómo intrigar. Es muy interesante descubrir qué es realmente una máquina pensante de la clase Perceptron.

Clasificación binaria (binaria) de objetos, neurona artificial de la clase Perceptron

Aquí está nuestra neurona artificial, divide los objetos en dos clases (realiza una clasificación binaria de los objetos):

Entonces tenemos:

• Entrada: objeto de muestreo - vector espacial m-dimensional $$$x = (x_1, ..., x_m)$
• Pesas $$$w = (w_1, ..., w_m)$ uno para cada característica del objeto de muestra (también un vector m-dimensional)
• Dentro: sumador $$$SUM = w_1x_1 + ... + w_mx_m = \ sum _ {j = 1} ^ {m} w_ {j} x_ {j}$ - suma ponderada de entradas de neuronas
• Siguiente: activación $$$Φ (x, w) = Φ (SUMA)$
• Aún más: cuantificador (umbral) - θ [theta]
• Activación + umbral: predicción de la etiqueta de clase de un objeto en función de la suma ponderada de las entradas de neuronas (atributos del objeto). Esta parte define la arquitectura específica de la neurona.
• Salida: etiqueta de clase de objeto (uno de dos) $$$\ hat {y} = \ {1, -1 \}$

Clasificación : porque una neurona asigna una clase a un objeto, binario ( binario ), porque solo hay dos clases posibles.

$$$\ hat {y}$ [juego con tapa]: denotaremos el valor de clase previsto (calculado) para el objeto $$$x$
$$$y$ [juego normal sin tapa] - valores de clase verdaderos (conocidos) para un objeto $$$x$ del conjunto de entrenamiento.

Valores $$$x$ (en adelante $$$x$ y $$$w$ - estos no son valores unitarios, sino vectores) varían de un objeto a otro, coeficientes de peso $$$w$ (una vez seleccionado) permanecen sin cambios. Para el conjunto de entrenamiento para cada objeto $$$x$ etiqueta de clase conocida $$$y$ . En la etapa de entrenamiento, debes elegir pesas $$$w$ para que el modelo produzca el valor correcto $$$\ hat {y}$ (coincidiendo con $$$y$ ) para el número máximo de objetos en el conjunto de entrenamiento. La suposición de la utilidad de una neurona entrenada de esta manera se basa en la esperanza de que produzca el valor correcto con los coeficientes seleccionados $$$\ hat {y}$ para nuevos objetos $$$x$ verdadero valor de clase $$$y$ para lo cual no se conoce de antemano.

El significado intuitivo de la suma ponderada de las entradas de una neurona es que todas las características del objeto (cada uno de los signos es una de las entradas de la neurona) afectan el resultado de la clasificación del objeto, pero no todos los signos se ven igualmente afectados. Hasta qué punto - determine el peso; poner a cero un determinado coeficiente de ponderación anula la contribución del atributo correspondiente a la cantidad total, es decir Esto equivale a eliminar la característica del objeto.

Neurona lineal adaptativa ADALINE

La neurona ADALINA (neurona lineal adaptativa) es una neurona artificial ordinaria con esta función de activación:

$$ $$Φ (x, w) = Φ (SUMA) = SUMA$$

$$ $$\ Phi (x ^ {(i)}, w) = \ Phi (\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)}) = \ sum _ { j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)}$$

En adelante superíndice $$$i$ entre paréntesis denotará $$$i$ elemento del conjunto de entrenamiento $$$x ^ {(i)}$ o verdadero valor de clase $$$y ^ {(i)}$ o valor de clase predicho $$$\ hat {y} ^ {(i)}$ para el

Podemos decir que dicha neurona simplemente no tiene una función de activación y el valor de la suma ponderada de las entradas se alimenta a la entrada del cuantificador (umbral). Pero para mantener la coherencia, será más conveniente suponer que el valor de la suma ponderada se toma como activación.

Umbral (cuantificador): predice una etiqueta de clase:

$$ $$\ hat {y} ^ {(i)} = \ left \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge \ theta \\ - 1, \ Phi (x ^ {(i)}, w) <\ theta \ end {matrix} \ right. $$$

Si el valor de activación es mayor que algún valor umbral θ [theta], entonces el cuantificador asigna la etiqueta "1" al objeto; si el valor de activación es menor que el umbral θ, el objeto recibe la etiqueta "-1".

Aquí podemos formular el problema en una primera aproximación : necesitamos seleccionar los parámetros de la neurona

• factores de ponderación $$$w_j, j = 1, .., m$
• y umbral θ [theta]

para que los valores de clase $$$\ hat y$ , que la neurona asigna a los objetos de la muestra de entrenamiento, coincidió con los valores verdaderos de las clases $$$y$ para los mismos elementos (o, al menos, dieron el significado correcto para la mayoría).

Transformamos un poco la función de umbral, tomemos el caso de la clase $$$\ hat y = 1$ y transfiera el umbral al lado izquierdo de la desigualdad:

$$ $$\ begin {ather} \ Phi (x ^ {(i)}, w) \ ge \ theta \ hfill \\\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {( i)} \ ge \ theta \ hfill \\ - \ theta + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 \ hfill \\ \ end {reunido}$$

denotar $$$w_ {0} = - \ theta$ y $$$x_ {0} = 1$

$$ $$\ begin {recolectado} w_ {0} x_ {0} ^ {(i)} + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 , w_ {0} = - \ theta, x_ {0} = 1 \ hfill \\\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0, x_ {0} = 1 \ hfill \ end {recolectado}$$

Como vemos, logramos deshacernos de un parámetro separado θ, introduciéndolo bajo la apariencia de un nuevo coeficiente de peso $$$w_0$ debajo del signo de la suma, mientras se agrega a la descripción del objeto un nuevo signo de unidad ficticia $$$x_0 = 1$ .

Corregiremos la formulación del problema teniendo en cuenta la nueva notación.

Tarea ' : seleccione los parámetros de la neurona - factores de ponderación $$$w_j, j = 0, .., m$ ,
$$$x_0 = 1$ (constante de signo) - neurona ficticia ( neurona de desplazamiento )

A partir de este lugar, numeramos los signos y los pesos c 0, no 1. Acerca del vector $$$w$ diremos que se trata de (m + 1) -dimensional, y no m-dimensional. Vector $$$x$ dependiendo del contexto, podemos considerar (m + 1) -dimensional (en su mayor parte en fórmulas), pero recuerde que, de hecho, es m-dimensional.

Por qué una neurona ( en nuestro caso, sin embargo, esto no es una neurona, sino un signo de un objeto o simplemente una entrada, pero en el caso de una red multicapa se convierte en una neurona y generalmente se llama así ) es ficticio , ahora está claro. Por qué también el desplazamiento se aclarará más tarde.

La activación con la suma ahora se verá así:

$$ $$\ Phi (x ^ {(i)}, w) = \ Phi (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}) = \ sum _ { j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}, x_ {0} ^ {(i)} = 1 \ para todos i$$

El umbral ahora es siempre 0 (cero) (el valor real se movió al parámetro $$$w_0$ ):

$$ $$\ hat {y} ^ {(i)} = \ left \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge 0 \\ - 1, \ Phi (x ^ {(i)}, w) <0 \ end {matrix} \ right. $$$

Una vez más formulamos el problema en otras palabras (el significado geométrico del problema)

Si observamos cuidadosamente la fórmula para la función de activación, veremos que es un hiperplano paramétrico en el espacio (m + 1) -dimensional, mientras que en las primeras m dimensiones coexiste con los puntos de los elementos de muestra, y (m + 1) - La dimensión electrónica es el espacio de valores de la función, separado de los elementos.

Ahora, si equiparamos el valor de activación a cero (valor de umbral), entonces esto también será un hiperplano, solo ya en el espacio m-dimensional, es decir. completamente en el espacio de valor del elemento $$$x$ . Este hiperplano separará los elementos. $$$x$ en dos grupos disjuntos.

Por lo general, en este lugar dicen que nuestra tarea es seleccionar los valores de los parámetros $$$w$ es decir construya un hiperplano m-dimensional en el espacio de elementos para que los elementos del conjunto de entrenamiento con el verdadero valor de la clase "1" estén en un lado del plano, y los elementos con la verdadera clase "-1" en el otro.

Para aquellos que no entienden lo que está escrito aquí, sigue leyendo: ahora todos veremos, esto es lo primero. En segundo lugar, también veremos que tal enunciado del problema, aunque válido, no está completamente completo.

Espacio unidimensional (m = 1)

Aquí es donde el código comienza a aparecer. Construimos todos los gráficos con la biblioteca Matplotlib habitual, pero aquí también uso la biblioteca Seaborn en una línea para ajustar el área del gráfico, porque Me gusta cómo lo hace, pero en principio puedes prescindir de ella.

# coding=utf-8 import matplotlib.pyplot as plt import seaborn as sns #      # (    -> ) sns.set(style='whitegrid', font_scale=1.8) #sns.set(style='whitegrid') #   ,   seaborn #plt.rcParams.update({'font.size': 16}) 

Tomamos muchos puntos unidimensionales y respuestas a ellos:

 import numpy as np import math #  -  ( ) X1 = np.array([1, 2, 6, 8, 10]) #   ( ) y = np.array([-1, -1, 1, 1, 1]) 

Aquí tenemos cada elemento i-ésimo de la matriz X1: este es el elemento i-ésimo (punto i-ésimo) de la muestra de entrenamiento (más precisamente, su primer y único atributo): $$$x ^ {(i)} = (X1 [i])$ , $$$x ^ {(i)} _ 1 = X1 [i]$

Cada elemento i-ésimo de la matriz y es la respuesta correcta, una etiqueta verdadera correspondiente al elemento i-ésimo de la muestra de entrenamiento con un solo atributo X1 [i].

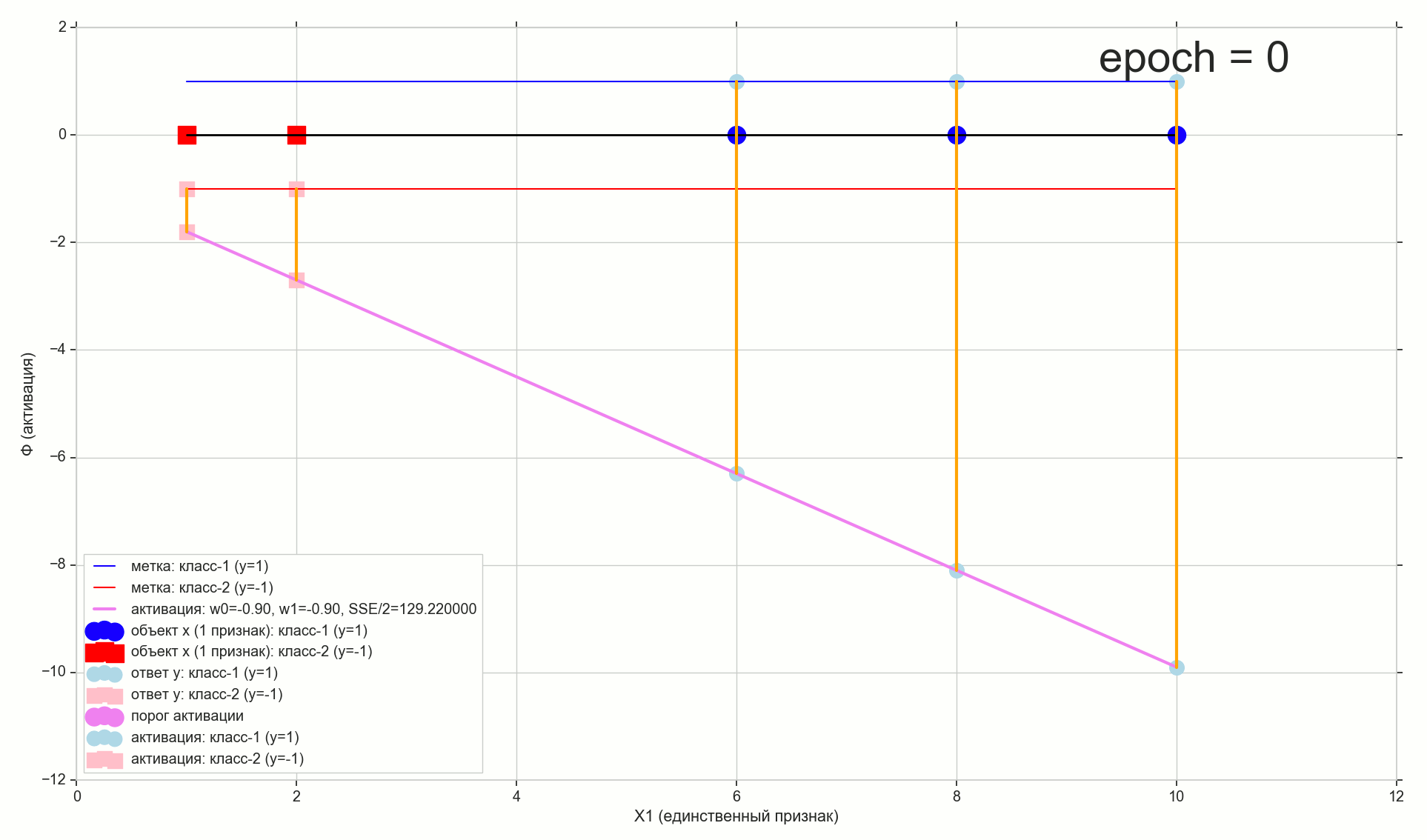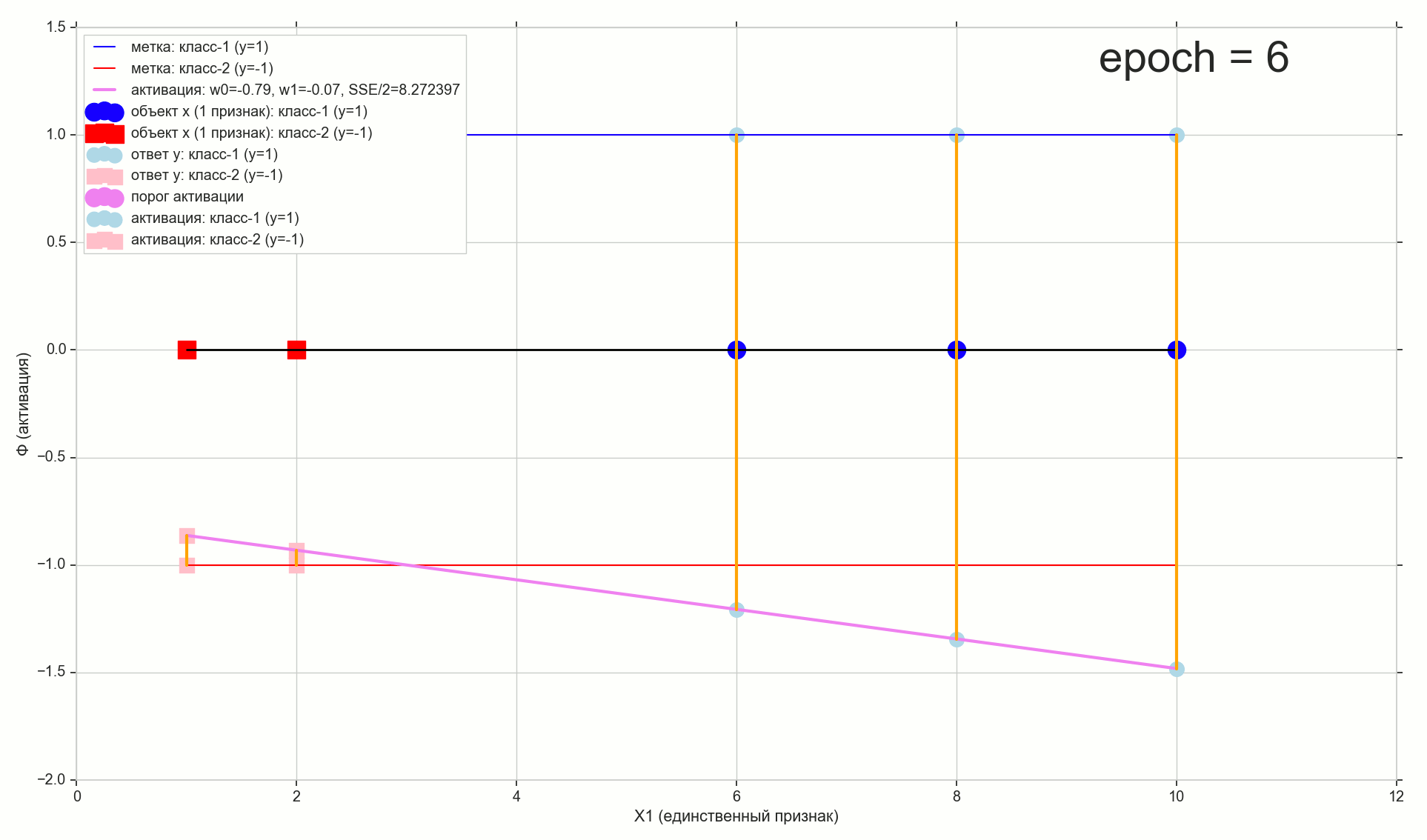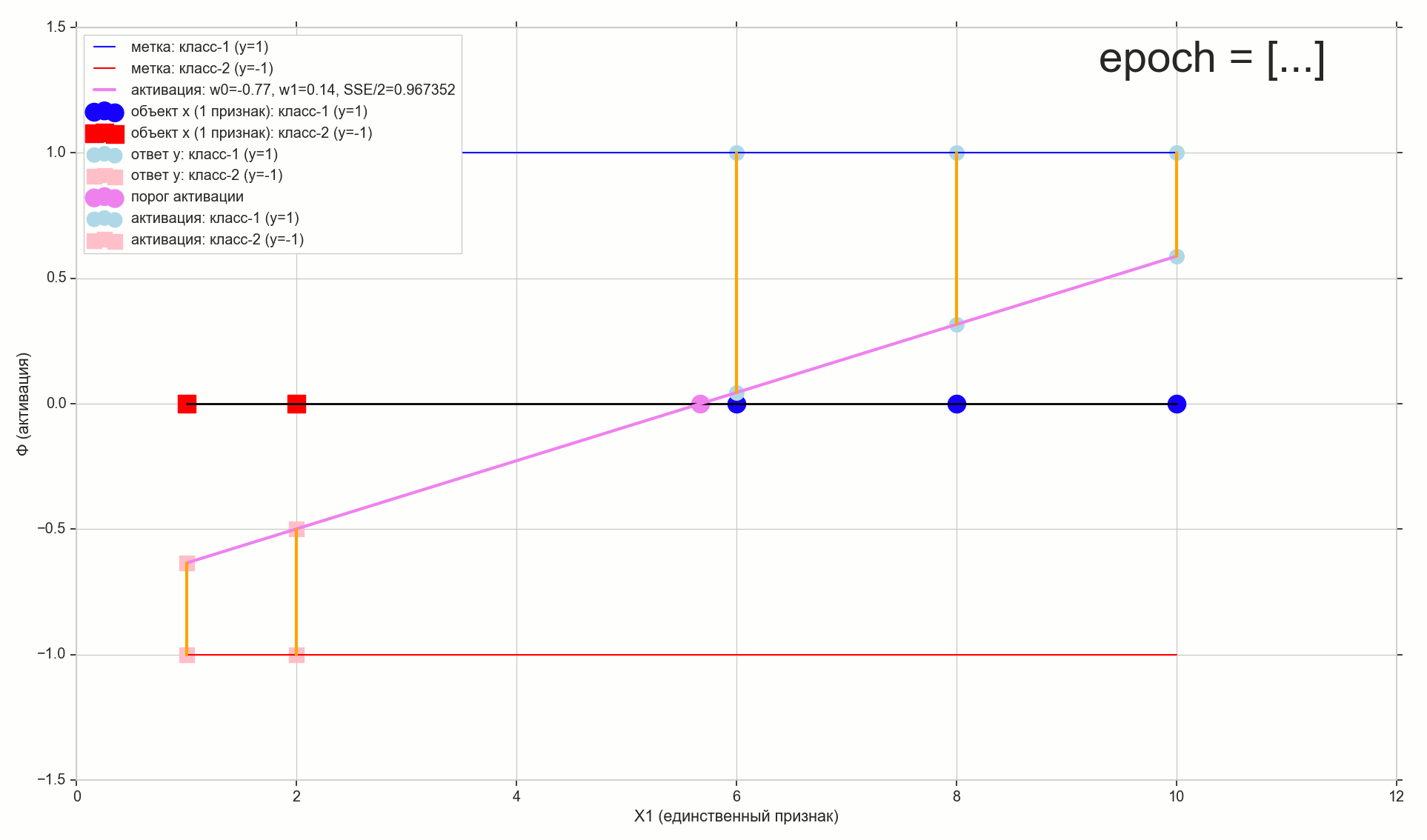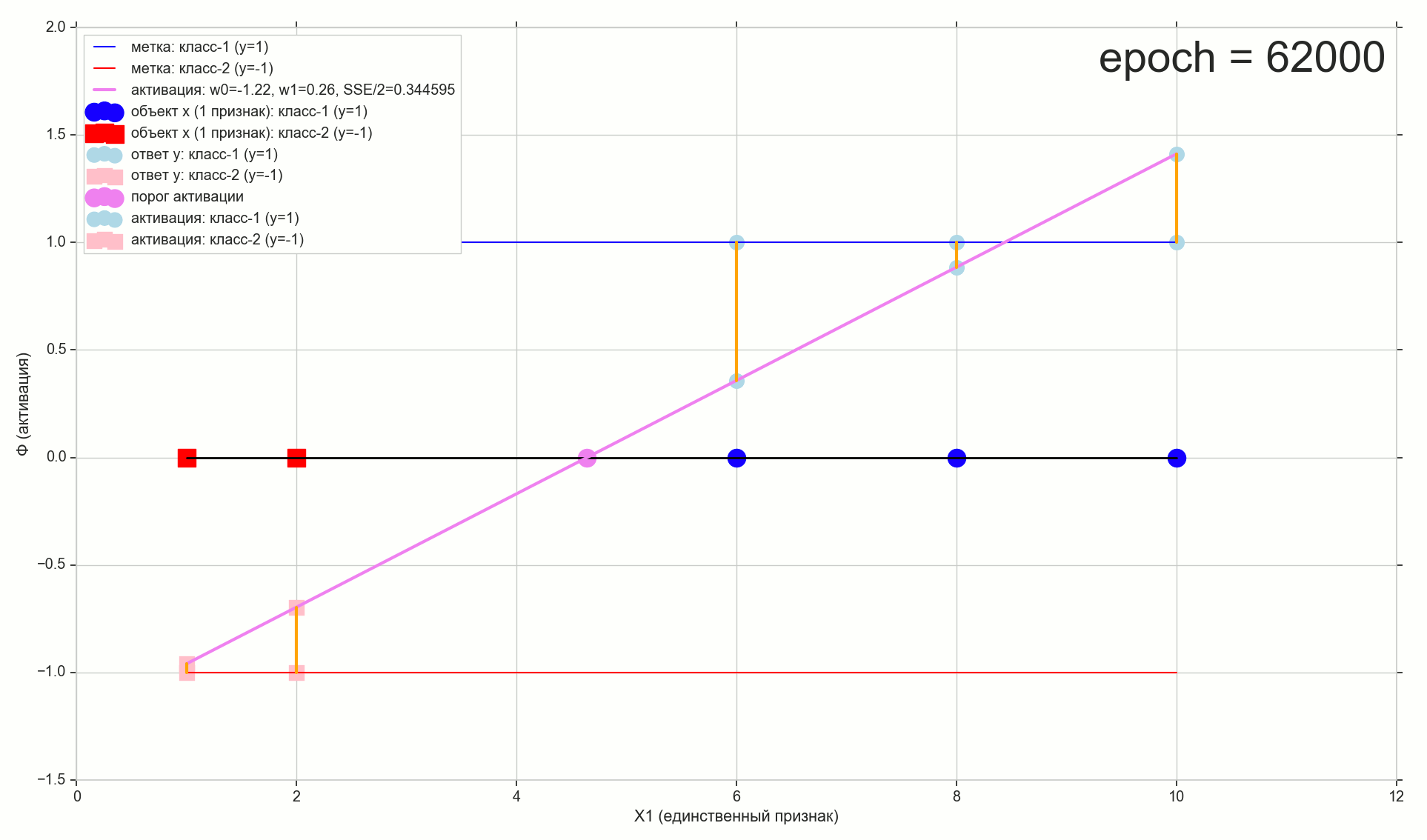
Tomamos solo 5 puntos, los dos primeros se asignan a la clase "-1", los tres restantes se asignan a la clase "1".

Dibuja estos puntos en la línea:

 #  =0 plt.plot(X1, np.zeros(len(X1)), color='black', lw=2) #     =0 plt.scatter(X1[y==1], np.full(len(X1[y==1]), 0), color='blue', marker='o', s=300, label=u' x (1 ): -1 (y=1)') plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), 0), color='red', marker='s', s=300, label=u' x (1 ): -2 (y=-1)') plt.xlabel(u'X1 ( )') plt.ylabel(u' ()') plt.legend(loc='upper left') plt.show() 

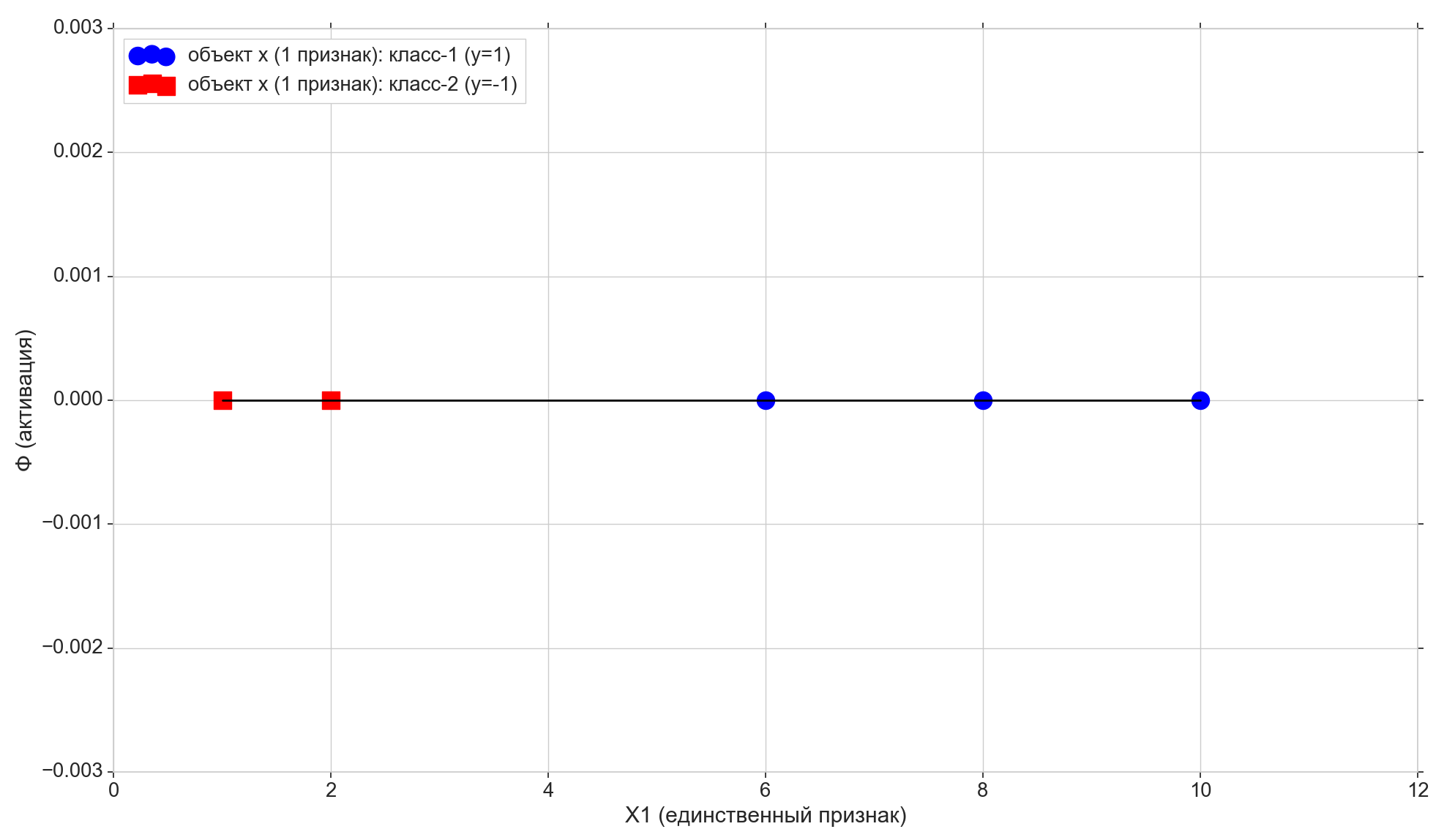
Ahora veamos la función de activación:

$$ $$\ Phi = w_ {0} + w_ {1} x_ {1}$$

Como puede ver, esta es una línea paramétrica ordinaria en el plano (en espacio bidimensional, es decir (m + 1) -dimensional):

• en el eje horizontal tenemos los puntos de los elementos (también son los valores del atributo X1)
• en vertical - valores de activación para cada elemento
• parámetro $$$w_1$ - establece el ángulo de inclinación,
• pero $$$w_0$ - Desplazarse a lo largo del eje vertical (aquí está la respuesta a la neurona de corte ).

 w0 = -1.1 w1 = 0.4 #  y_ = w0 + w1*X1 #   (   -    ) plt.plot(X1, y_, color='violet', lw=3, label=u': w0=%0.2f, w1=%0.2f, sse/2=%0.2f'% (w0, w1, sse/2)) # :    =0 plt.scatter([-w0/w1], [0], color='violet', marker='o', s=300, label=u' ') #       plt.scatter(X1[y==1], y_[y==1], color='lightblue', marker='o', s=200, label=u': -1 (y=1)') plt.scatter(X1[y==-1], y_[y==-1], color='pink', marker='s', s=200, label=u': -2 (y=-1)') 

Recuerde también que después de una pequeña conversión, nuestro umbral de activación se convirtió en cero. Por lo tanto, si la proyección del elemento i-ésimo en la línea de activación es inferior a cero, asignamos la clase -1 al elemento ( $$$\ hat {y} = -1$ ), si es mayor que cero, asignamos la clase "1" ( $$$\ hat {y} = 1$ )

Punto morado: intersección de la línea de activación con el eje $$$\ Phi = 0$ , separando elementos de diferentes clases, este es el hiperplano muy separador (para el espacio unidimensional, el punto es el hiperplano) construido en el espacio de características unidimensional (es decir, m-dimensional). Como puede ver, para dividir los elementos en grupos, es suficiente, pero para asignar clases a grupos, ya no es suficiente. Para asignar clases a los elementos, necesitamos una activación directa (hiperplano bidimensional) construida en el espacio 2-d (es decir, en el (m + 1) -d) "signos + activación": la dirección de la desviación de activación desde la vertical axis determinará la clase para grupos de elementos, porque depende de si las proyecciones de los elementos en la activación son mayores o menores que cero.

Cambio de parámetros $$$w_0$ y $$$w_1$ Recibiremos diferentes líneas de activación. Necesitamos construir tal línea de activación, es decir encontrar tal combinación de parámetros $$$w$ en el que la proyección de los dos primeros puntos de la muestra de entrenamiento en la línea de activación es inferior a cero (para ellos, el valor $$$\ hat {y} = y = -1$ ), y la proyección de los 3 puntos restantes será superior a cero (para ellos $$$\ hat {y} = y = 1$ )

Es bastante obvio que en nuestro caso particular no hay nada complicado en la construcción de una línea de este tipo, además, tales líneas generalmente se pueden construir en un número infinito. Pero intentaremos construirlo de tal manera que se satisfaga algún criterio de optimización (puede afectar la calidad de las predicciones futuras), además de que debería existir la capacidad de extender el algoritmo al caso multidimensional.

Aquí también observamos que seleccionamos específicamente el conjunto inicial de puntos para que pueda dividirse por dicha línea (para 1-e: todos los elementos del primer grupo son más pequeños, todos los elementos del segundo grupo son más grandes que algún valor fijo), es decir Muchos puntos de entrenamiento son linealmente separables .

Agregue dos líneas horizontales más al gráfico correspondiente a las clases {1, -1}, y proyecte los elementos sobre ellas.

 #      (y=1, y=-1) plt.plot(X1, np.full(len(X1), 1), color='blue', label=u': -1 (y=1)') plt.plot(X1, np.full(len(X1), -1), color='red', label=u': -2 (y=-1)') #       (y=1, y=-1) plt.scatter(X1[y==1], np.full(len(X1[y==1]), 1), color='lightblue', marker='o', s=200, label=u' y: -1 (y=1)') plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), -1), color='pink', marker='s', s=200, label=u' y: -2 (y=-1)') 

Puntos con proyecto de clase "-1" a la línea de fondo $$$\ Phi = -1$ , apunta con el proyecto de clase "1" a la línea superior $$$\ Phi = 1$ .

Prestemos atención a un pequeño matiz más. Trazamos los valores de activación a lo largo del eje vertical, el espacio de valores de activación es continuo. Pero el resultado del clasificador (la función de activación pasada a través del umbral) es un conjunto discreto de dos elementos {-1, 1}, y no una escala continua. Aquí tomamos un conjunto discreto de clases $$$y$ y ponerlo en una escala de activación continua $$$\ Phi$ para que los valores de clase discretos se conviertan en puntos ordinarios en la escala de activación, casos especiales de valores de activación que puede aceptar directamente o acercarse lo suficiente a ellos. Estrictamente hablando, inicialmente podríamos tomar no los valores numéricos como clases, sino las etiquetas de cadena "clase-1" y "clase-2", en cuyo caso tendríamos que hacer coincidir las etiquetas de cadena con los valores numéricos en la escala de activación. Por lo tanto, en nuestro caso, los valores de las clases "-1" y "1" deben tomarse no como etiquetas de clase como son, sino como un mapeo de clases marcadas a la escala de activación.

Es hora de ingresar la métrica de error

 #   -       #      plt.plot([X1, X1], [y_, y], color='orange', lw=3)#, label='err') 

Es natural aceptar que cuanto más cercano esté el valor de activación para el elemento seleccionado al valor de clase para el mismo elemento, mejor predice la clase de activación para este elemento. Por lo tanto, para el error del elemento seleccionado, puede tomar la distancia entre los puntos: la proyección vertical del elemento en la línea de activación y la proyección del elemento en la línea horizontal de su clase conocida (verdadera). En el gráfico: errores - líneas verticales naranjas.

Función de costo (pérdida)

Tenemos una métrica de error para cada artículo individual. Podemos obtener una métrica de calidad para toda la línea de activación. Es bastante natural aceptar, por ejemplo, que cuanto menor es la suma de los errores de todos los elementos de la muestra de entrenamiento, mejor hemos construido una línea de activación. Para cada elemento individual, el error no será mínimo, pero para toda la muestra de entrenamiento en su conjunto, puede llegar a un compromiso.

Pero no puede tomar una simple suma de errores, sino la suma de los errores al cuadrado ( suma de errores al cuadrado, suma de errores al cuadrado, SSE ). Es bastante obvio que, como en el caso de la suma de errores ordinarios, cuanto más cerca esté la línea de activación de los puntos con verdaderas clases de elementos, menor será la suma de los errores cuadráticos, pero en el caso de un error cuadrático, los elementos más remotos recibirán una penalización más severa.

De hecho, lo que nos interesa aquí no es el tamaño de la multa para elementos distantes, sino el hecho de que la función cuadrática tiene un mínimo y es diferenciable en todas partes (la suma habitual tendrá un mínimo, pero en este mínimo no será diferenciable), vea por qué esto es necesario. un poco mas tarde

Entonces

• Error: distancia del valor de la etiqueta de clase al hiperplano de activación
• SSE: la suma de los errores cuadráticos de todos los elementos de la muestra de entrenamiento
• Función de costo $$$J (w)$ - métrica de calidad para la línea de activación seleccionada. Cuanto menor sea el valor, mejor será la activación.

Tomar en función del valor $$$1 \ más de 2$ SSE, en el caso general de una neurona lineal, se verá así:

$$ $$\ begin {ather} J (w) = {1 \ over 2} SSE = {1 \ over 2} \ sum _ {i = 1} ^ {n} (\ Phi (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}) - y ^ {(i)}) ^ {2} = {1 \ over 2} \ sum _ {i = 1} ^ {n} (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} - y ^ {(i)}) ^ {2} \ end {reunido}$$

( $$$1 \ más de 2$ en primer lugar, no interfiere con SSE y, en segundo lugar, por conveniencia: se reducirá maravillosamente aún más)

Aqui $$$i$ - número de elemento, y $$$n$ - el número de elementos en el conjunto de entrenamiento. Déjame recordarte que $$$y ^ {(i)}$ - clase verdadera $$$i$ elemento de la muestra de entrenamiento, es decir conocida respuesta correcta de antemano.

Como recordamos, la posición de la línea de activación está determinada por los parámetros: factores de ponderación $$$w$ por lo tanto vector $$$w$ Actúa como un parámetro de la función de pérdida.

Para caja unidimensional

$$ $$J (w) = {1 \ over 2} SSE = {1 \ over 2} \ sum_ {i = 1} ^ {n} (w_ {0} + w_ {1} x_ {1} ^ {(i) } -y ^ {(i)}) ^ {2}$$

Valores $$$x$ y $$$y$ son conocidos de antemano (este es un conjunto de entrenamiento), por lo tanto, son fijos. Seleccionamos los parametros $$$w$ es decir $$$w_0$ y $$$w_1$ para que el valor $$$J (w)$ Resultó ser mínimo. Tratemos de trazar el gráfico como un valor $$$J (w)$ depende de los parámetros $$$w_0$ y $$$w_1$

 #      w0 = np.linspace(-10, 10, 200) w1 = np.linspace(-1, 1, 200) # https://docs.scipy.org/doc/numpy/reference/generated/numpy.meshgrid.html # https://stackoverflow.com/questions/36060933/matplotlib-plot-a-plane-and-points-in-3d-simultaneously ww0, ww1 = np.meshgrid(w0, w1) sse = [] for j in range(len(w1)): sse.append([]) for i in range(len(w0)): sse[j].append(((ww0[j][i]+ww1[j][i]*X1 - y)**2).sum()) sse = np.array(sse) # https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html # https://matplotlib.org/api/toolkits/mplot3d.html from mpl_toolkits.mplot3d import axes3d fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.set_xlabel('w0') ax.set_ylabel('w1') ax.set_zlabel('J(w)') #ax.plot_surface(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8) ax.plot_wireframe(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8, label='SSE/2') plt.xlim(-10., 10.) plt.ylim(-1., 1.) plt.legend() plt.show() 

En general, ya es visible aquí que la función de pérdida tiene un mínimo, y dónde se encuentra aproximadamente. Pero hagamos un truco más y construyamos el mismo gráfico, solo con una escala vertical logarítmica .

 #ax.plot_surface(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8) ax.plot_wireframe(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8, label='log(SSE/2)') 

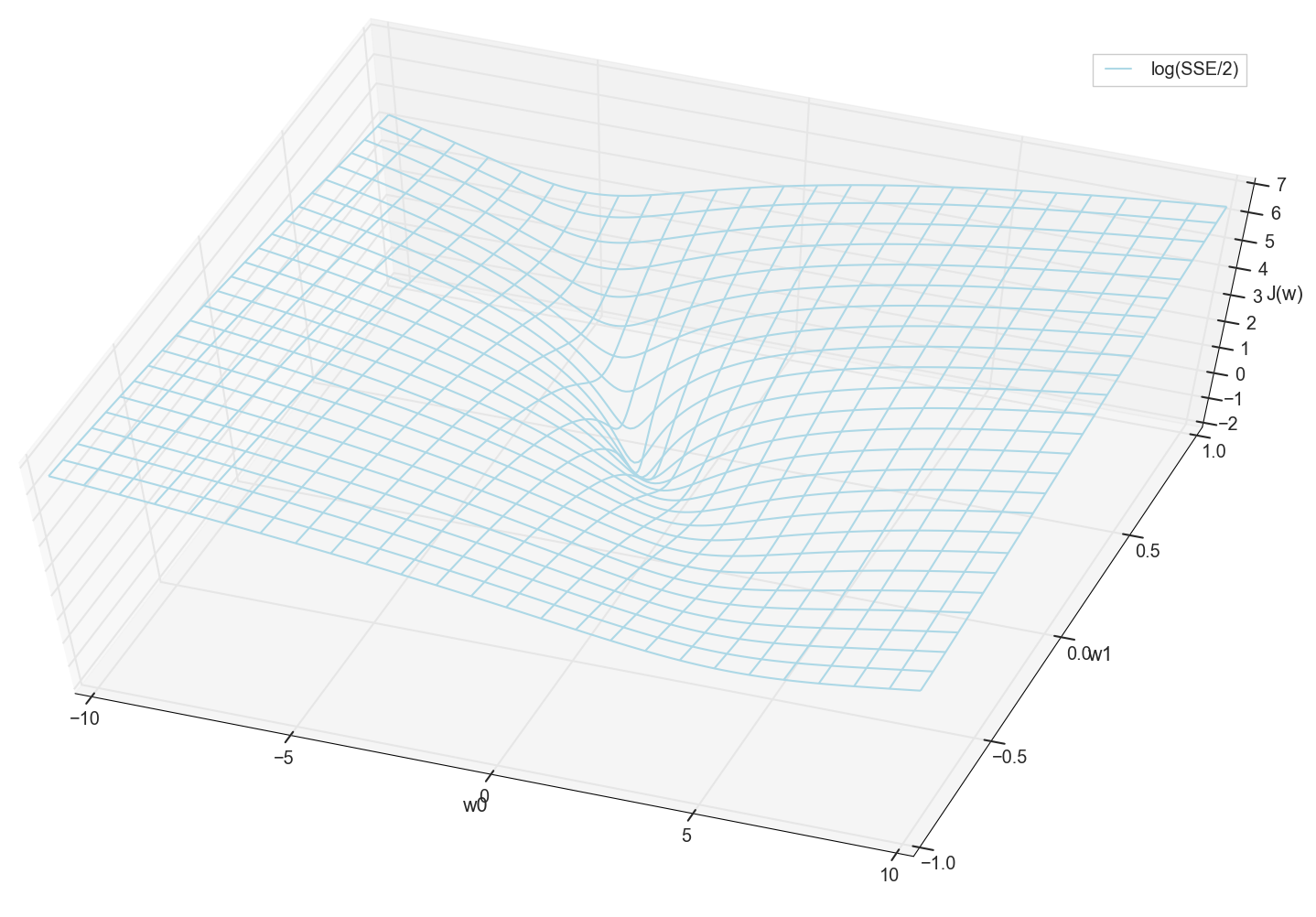
No sé sobre ti, pero personalmente, cuando vi este cuadro por primera vez, experimenté la iluminación. Esta cavidad natural no es solo una visualización figurativa de colinas multidimensionales de un artículo popular sobre redes neuronales, es un gráfico real.

Nuestra tarea es seleccionar tales valores $$$w_0$ y $$$w_1$ para llegar al fondo de este pozo. Obtenemos los valores de los pesos, obtenemos una neurona entrenada.

Como todos trazamos un gráfico y observamos personalmente su mínimo, nadie nos prohibirá encontrar sus coordenadas mediante una simple enumeración en la cuadrícula "manualmente":

 #      # https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.min.html # https://docs.scipy.org/doc/numpy/reference/generated/numpy.amin.html#numpy.amin # https://docs.scipy.org/doc/numpy/reference/generated/numpy.argmin.html min_ind = np.unravel_index(np.argmin(sse), sse.shape) #  -  #ax.scatter(ww0[min_ind], ww1[min_ind], sse[min_ind]/2, color='red', marker='o', s=100, ax.scatter(ww0[min_ind], ww1[min_ind], math.log(sse[min_ind]/2), color='red', marker='o', s=100, label='min: w0=%0.2f, w1=%0.2f, SSE/2=%0.2f' % (ww0[min_ind], ww1[min_ind], sse[min_ind]/2)) 

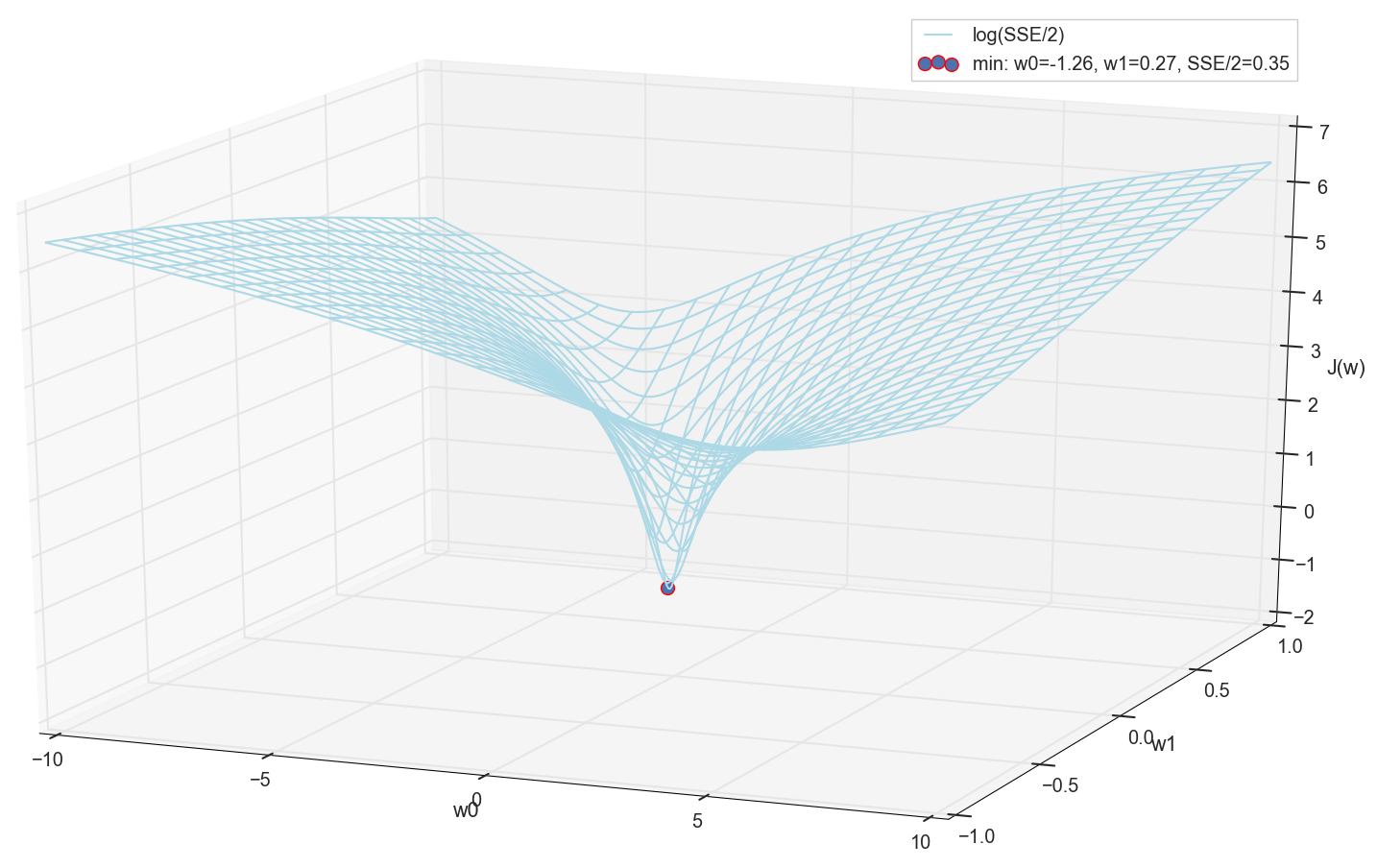
Estos son los valores: $$$w_0 = -1.26$ y $$$w_1 = 0.27$ , la suma de los errores cuadrados del SSE es 0.69, la función de costo $$$J (w) = SSE / 2 = 0.35$ (Más precisamente: 0.3456478371758288).

Veamos cómo se ve la activación con estos parámetros:

 #  ""   (SSE=0.69, sse/2=0.345) w0 = -1.26 w1 = 0.27 

En cuanto a mí, es bastante normal. El punto de intersección de activación con un umbral cero separa elementos de diferentes clases, y la activación misma les asigna los valores correctos. Al mismo tiempo, la activación parece estar en una posición óptima.

Antes de continuar, nuevamente admiramos el gráfico en la cuadrícula:

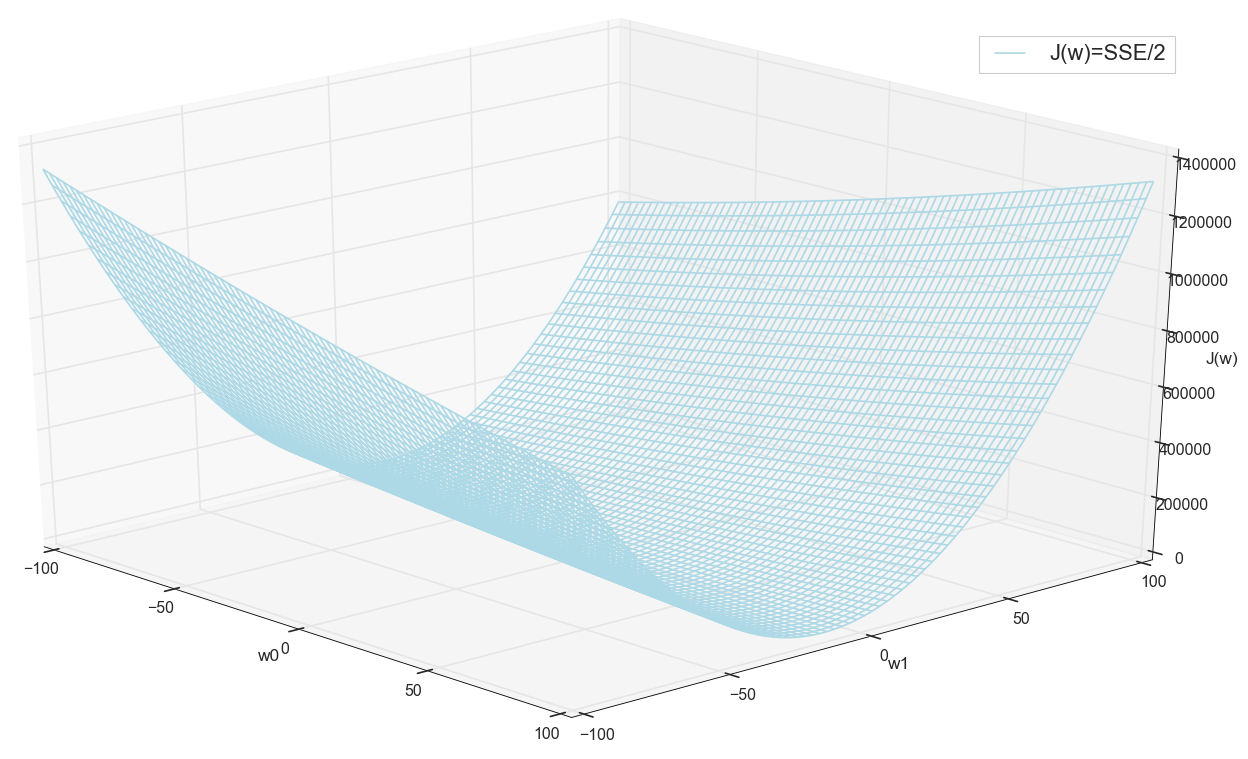
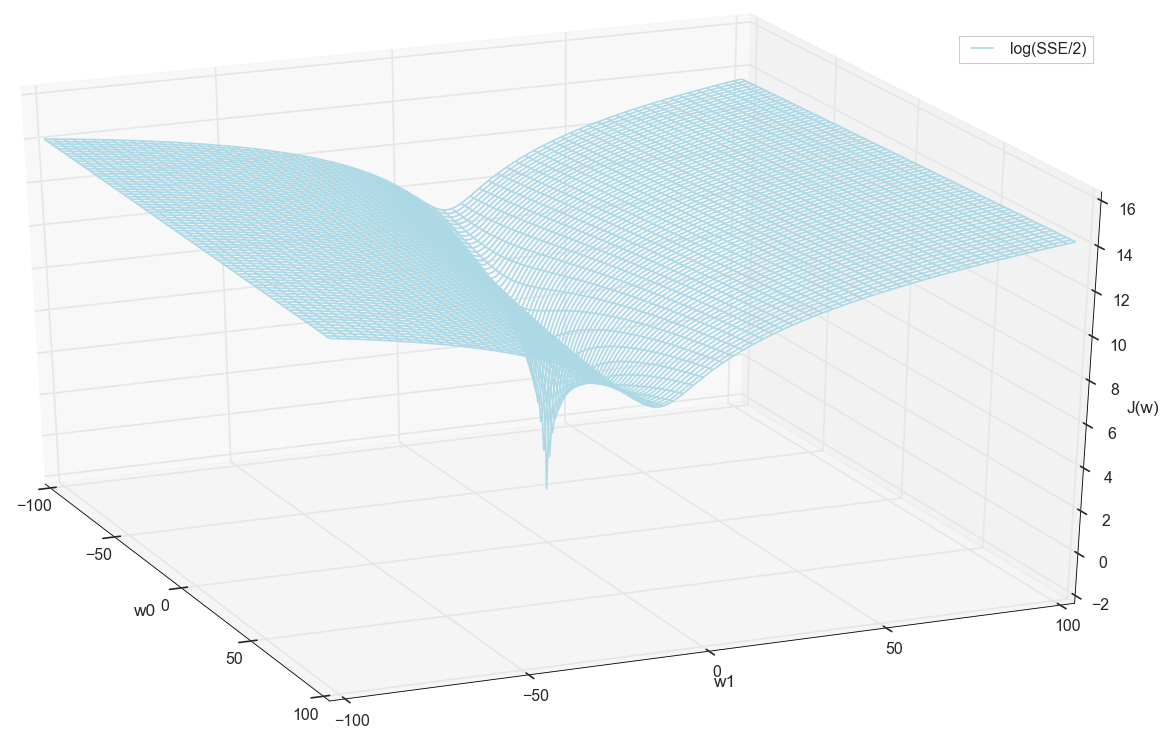
Parece que no hay otros mínimos cercanos que hubieran pensado.

Búsqueda mínima

Entonces, obtuvimos pesos: las coordenadas del valor mínimo de error. Este será el valor óptimo de los pesos en la muestra de entrenamiento. En términos generales, esto es exactamente lo que necesitamos, podemos decir que la neurona está entrenada. Tal vez esto se puede completar?

Busque un mínimo: busque por cuadrícula

• La opción a primera vista funciona bastante (como vemos)
• Debe saber de antemano el área donde buscar un mínimo (puede tomar bordes bastante grandes y luego reducir el área de búsqueda; esto es solo a simple vista)
• Para aumentar la precisión, debe disminuir el paso → incluso más puntos (solución: puede reducir de forma iterativa el área de búsqueda)
• Demasiados puntos (para 2d puede estar bien, pero para casos multidimensionales nos encontramos con recursos muy rápidamente)
• Para MNIST (28x28 = 784 píxeles: el mismo número de entradas, los mismos factores de ponderación más el desplazamiento, una cuadrícula de 100 pasos por dimensión): 100 ^ 785 = 10 ^ 1570.

Entonces, si queremos entrenar una sola neurona (ni siquiera una red neuronal) en una imagen de 28x28 = 784 píxeles buscando un mínimo por enumeración directa en una cuadrícula de 100 puntos para cada medición, necesitamos resolver 10 ^ 1570 combinaciones. Esto es bastante para el almacenamiento y la búsqueda (en la parte visible del Universo solo hay 10 ^ 80 átomos, el Universo existe durante aproximadamente 4 * 10 ^ 17 segundos = 4 * 10 ^ 26 nanosegundos).

Intentemos encontrar una opción más rápido.

Búsqueda mínima: descenso constante

Veamos el gráfico de la función de pérdida. $$$J (w)$ en el avión: arreglar $$$w_0$ cambiar $$$w_1$

 def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum() #  w0,   J(w1)=sse(w1)/2 w1 = np.linspace(-1, 1, 200) sse = [[], [], []] for i in range(len(w1)): sse[0].append(sse_(X1, y, -1, w1[i])) sse[1].append(sse_(X1, y, 0, w1[i])) sse[2].append(sse_(X1, y, 1, w1[i])) sse = np.array(sse) plt.plot(w1, sse[0]/2, color='orange', label='w0=-1') plt.plot(w1, sse[1]/2, color='blue', label='w0=0') plt.plot(w1, sse[2]/2, color='red', label='w0=1') plt.xlabel('w1') plt.ylabel('J(w)') plt.legend() plt.show() 

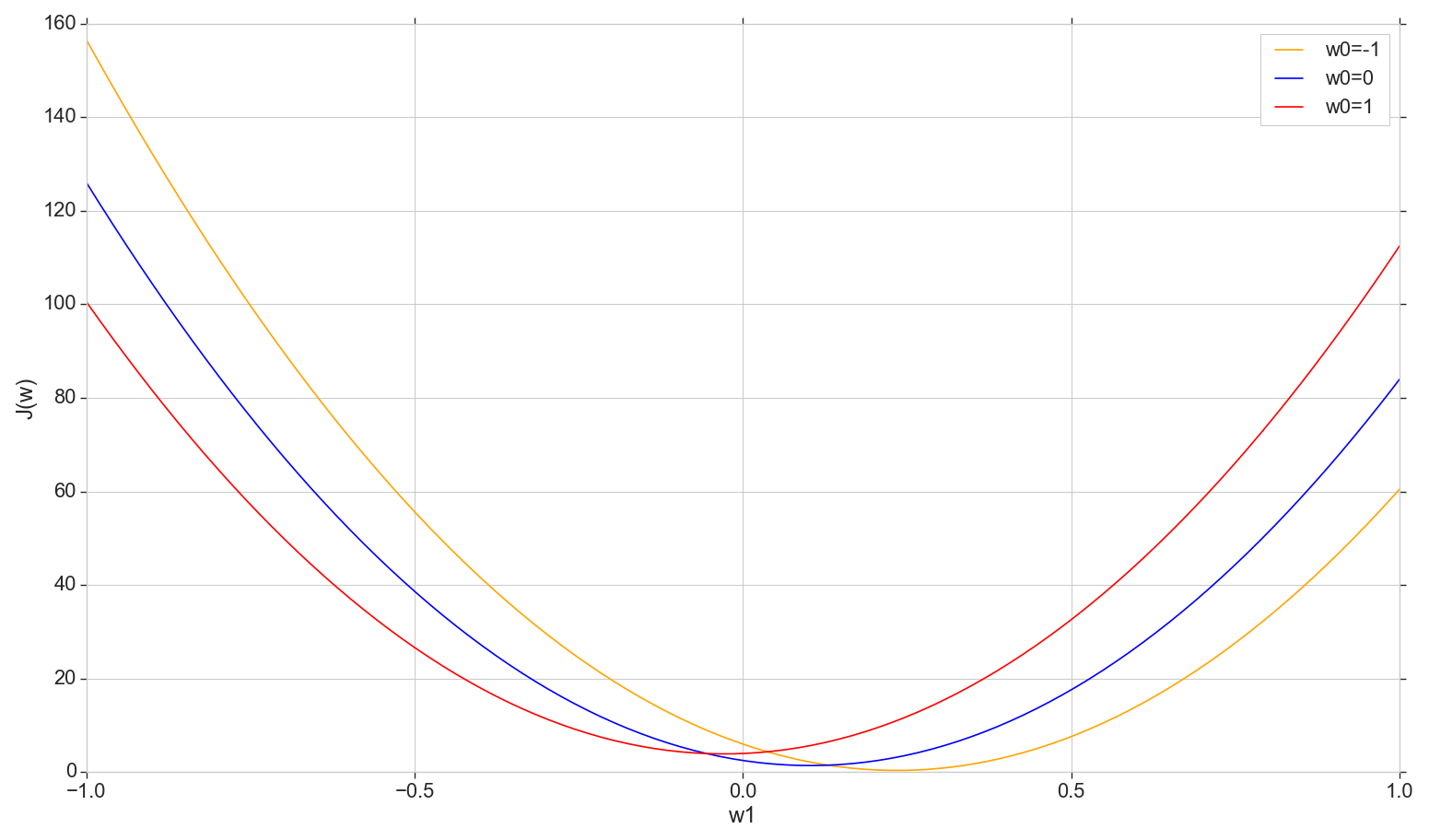
Esta es una parábola ordinaria (más precisamente, una familia de parábolas; diferirán ligeramente dependiendo de qué tipo de valor se fije en $$$w_0$ ) Para encontrar la parábola mínima, no es necesario clasificar todos los puntos. Podemos elegir un punto arbitrario en el eje horizontal y movernos hacia el mínimo con algún paso.

Considere una opción de tono constante

• Si el paso es demasiado grande, puede fallar y no alcanzar el mínimo (el paso se puede reducir)
• Si es demasiado pequeño, habrá demasiados pasos (más de lo que podría ser)
• En cualquier caso, no alcanzaremos el mínimo exacto, pero podemos lograrlo con una precisión arbitraria cambiando el paso cerca del mínimo inexacto encontrado (el paso deja de ser constante)
• No sabemos la dirección del descenso (es posible resolver algorítmicamente: no avance hacia el aumento de errores)
• El problema para encontrar el rango se ha resuelto (puede bajar desde cualquier lugar; tarde o temprano, bajaremos de todos modos)
• En principio, la opción está funcionando, pero ¿tal vez hay una mejor opción?

Nota: cuando hablé sobre tal opción de descender a una conferencia, un estudiante preguntó por qué necesita avanzar en pasos si puede encontrar inmediatamente una parábola mínima usando la fórmula. Al principio, respondí algo con el espíritu de que ahora estamos interesados ​​en considerar la opción de iteración, para que luego podamos usarla no solo con una parábola, sino también en otras situaciones. Además, de hecho, no necesitamos al menos una parábola específicamente en esta sección: nos moveremos al mínimo no en una dimensión, sino en todas las dimensiones de tal manera que en cada nueva iteración se produzca un nuevo paso no a lo largo de esta parábola, sino en parábola con una nueva rebanada con un valor desplazado $$$w_0$ . Pero pensando más tarde, pensé que, en principio, no hay nada de malo si nos movemos en cada corte, no en pasos, sino que bajamos inmediatamente al mínimo del corte actual. Entonces, una y otra vez, medida por medida, todavía tenemos que deslizarnos a un mínimo global, y parece más rápido que los pasos. Para una sola neurona, debería funcionar, y no solo con una parábola. Pero aún no he empezado a perder el tiempo probando esta teoría, así que aquí seguimos adelante: prometí hablar sobre el descenso de gradiente.

Busque un mínimo: descenso en gradiente

En general, bajamos los escalones, pero lo hacemos de manera más inteligente. Utilizamos la derivada de la curva de costo para seleccionar el paso (aquí, no la curva de costo , sino la curva de costo ).

• Tenemos varias dimensiones y cada una de ellas tiene su propia curva: arreglamos todo $$$w_j$ excepto $$$w_k$ ,
• $$$J (w_k)$ habrá una curva de error en $$$k$ th dimension
• Todos ellos son (en nuestro caso) parábolas, pero, en términos generales, solo es importante que sean diferenciables en todas partes y tengan un mínimo
• Para ajustar el paso en cada medición, utilizaremos la derivada parcial de la función de error con respecto a esta medición (un coeficiente variable $$$w_k$ )
• Un vector de tales derivados parciales se llama gradiente.

Todo esto es bueno, pero ¿de dónde viene la derivada? Ahora vamos a resolverlo.

El significado geométrico de la derivada.

Para mí, la derivada durante mucho tiempo siguió siendo un conjunto de fórmulas y reglas especiales para su cálculo, además de algo sobre el aumento, la disminución y los extremos. Será apropiado recordar o descubrir cuál es la derivada en realidad.

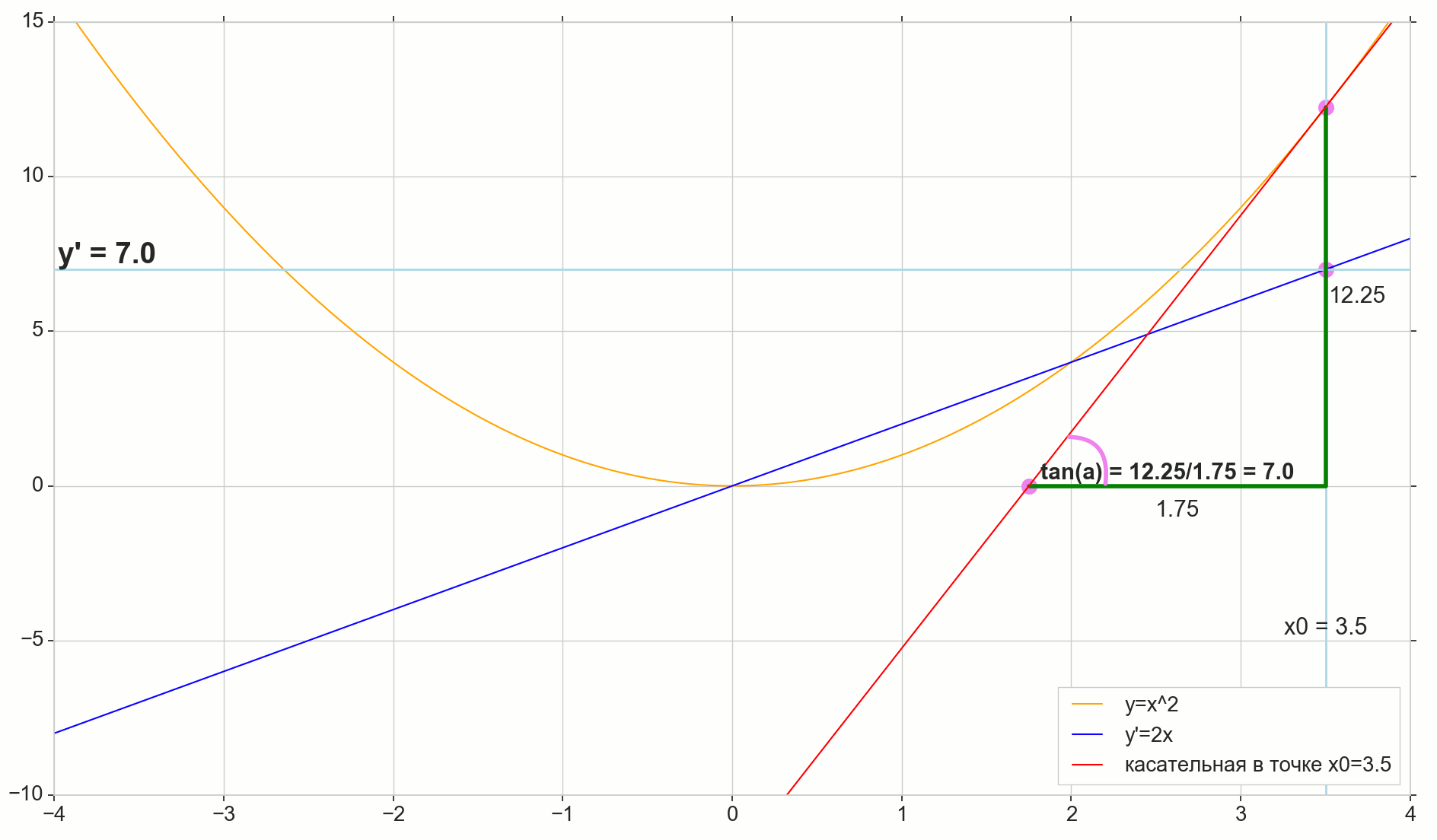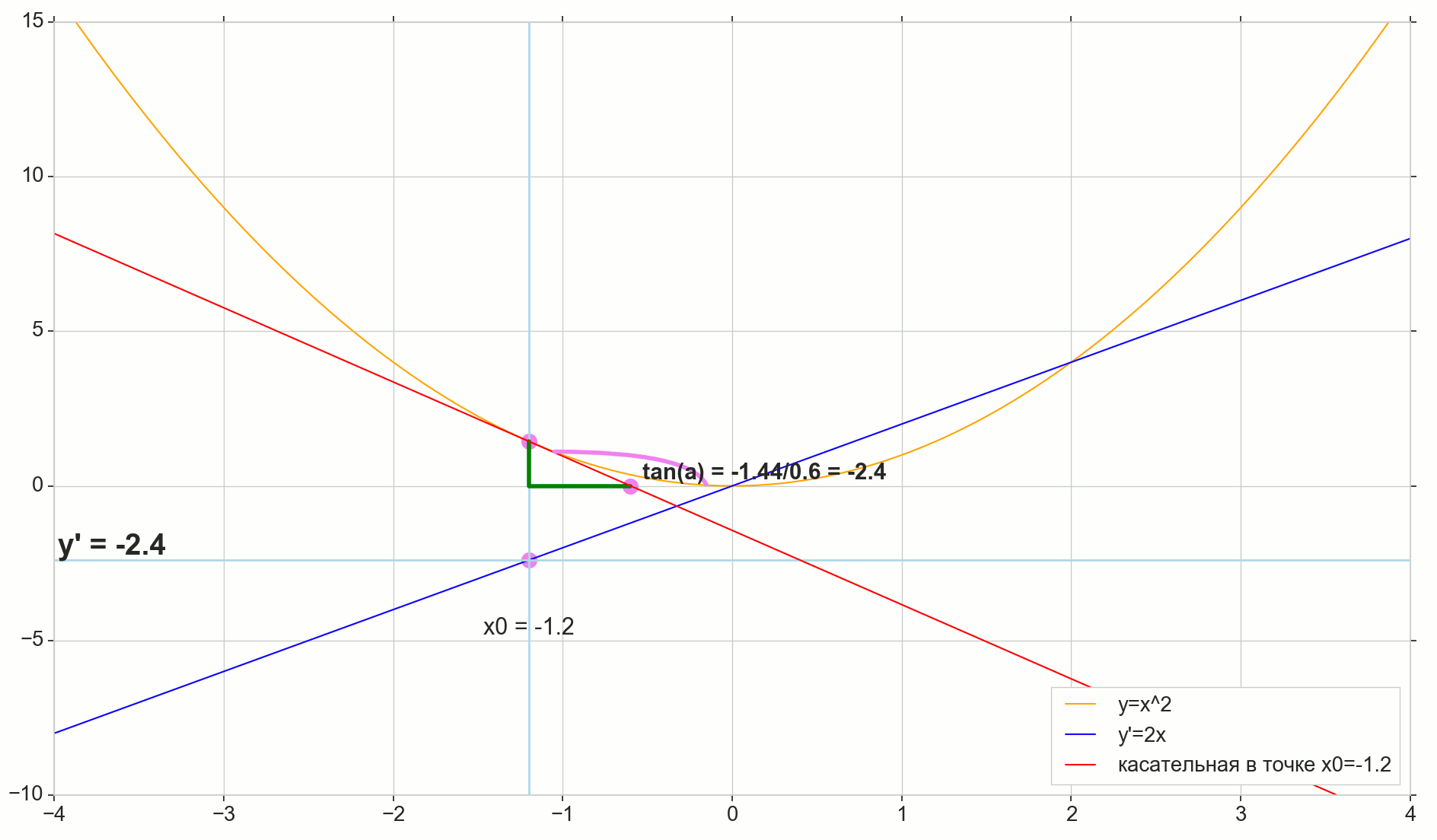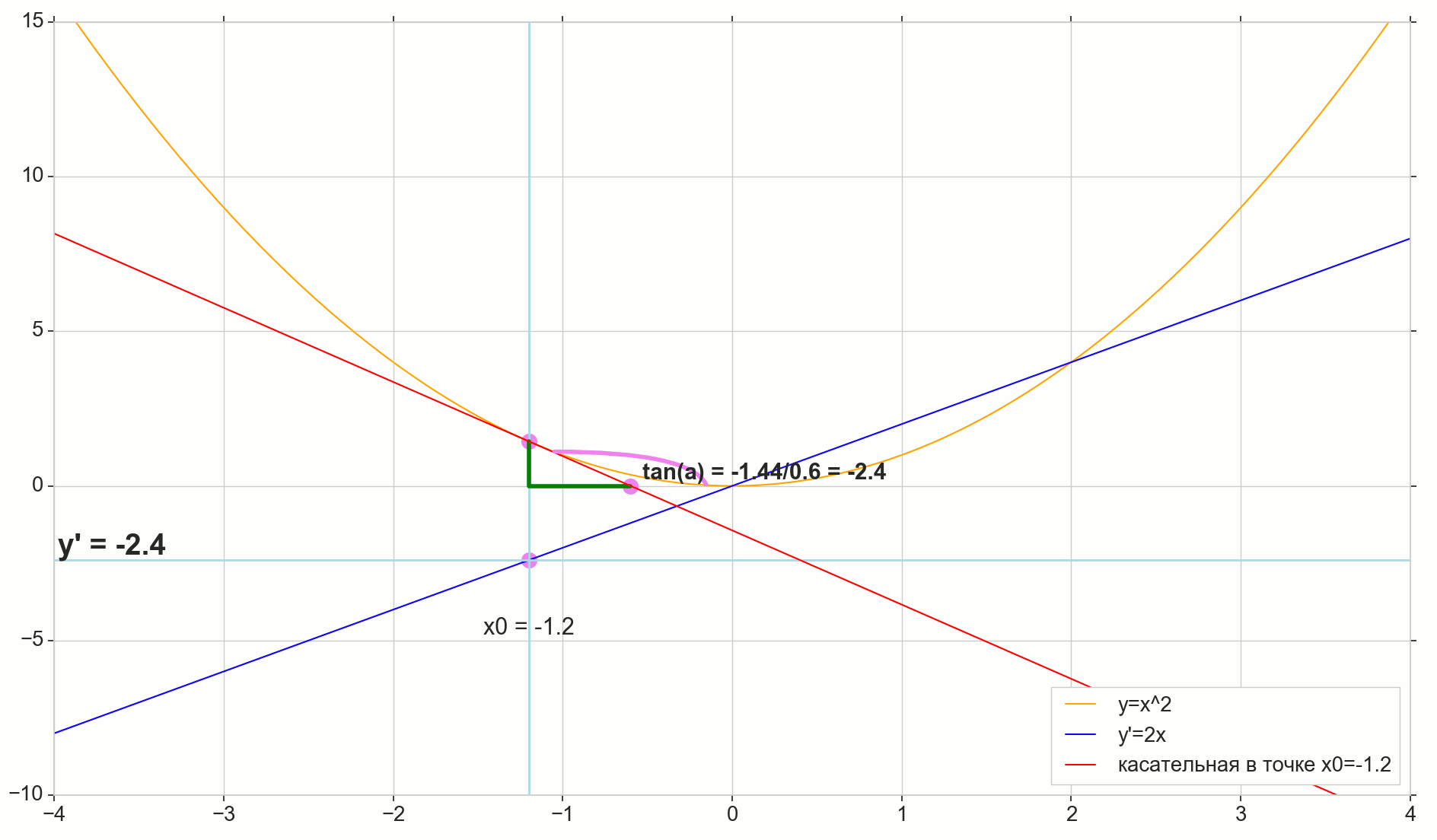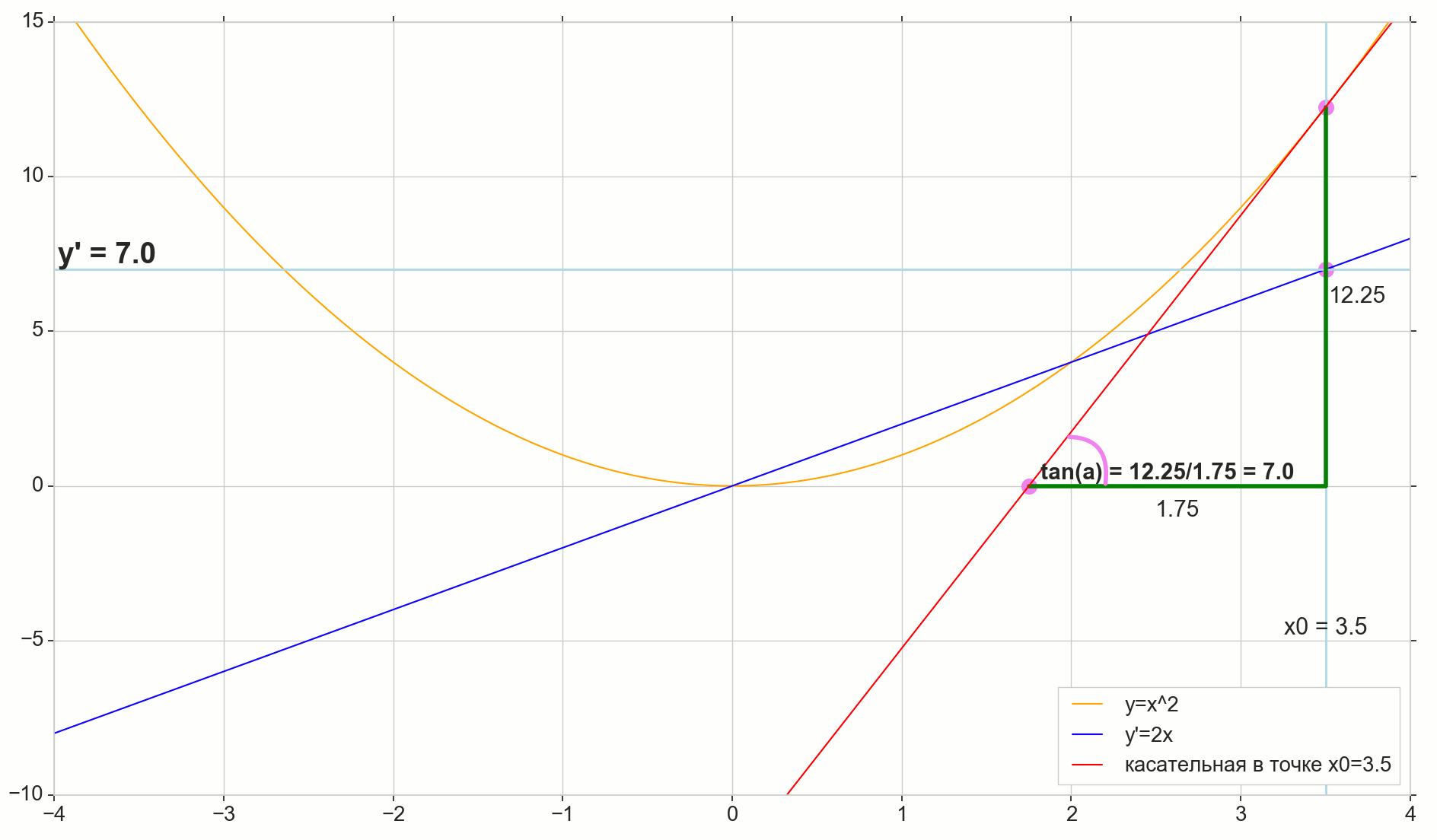
Función derivada $$$y (x)$ en este punto $$$x_0$ Es el límite de la relación del incremento de la función. $$$\ Delta y$ al incremento de argumento $$$\ Delta x$ al incrementar un argumento $$$\ Delta x$ tendiendo a cero:

$$ $$y '(x_0) = \ lim _ {\ Delta x \ to 0} {\ Delta y \ over \ Delta x}, \ Delta y = y (x_0 + \ Delta x) - y (x_0)$$

El punto en la foto $$$M (x_0, y (x_0)) = (x_0, y_0)$ Es el punto en el que queremos determinar la derivada. Punto $$$N (x_0 + \ Delta x, y (x_0 + \ Delta x)) = (x_0 + \ Delta x, y_0 + \ Delta y)$ - punto obtenido al incrementar el argumento $$$\ Delta x$ . Directo $$$Mn$ - secante que pasa por estos dos puntos.

Punto $$$A$ - intersección de secante $$$Mn$ con eje horizontal $$$y = 0$ .

Considere dos triángulos rectángulos: un triángulo $$$\ triangle NPM$ con sección secante $$$Mn$ como una hipotenusa y un triángulo $$$\ triangle MBA$ con la continuación de la secante al eje $$$y = 0$ - segmento $$$AM$ como una hipotenusa Del curso de grafía y geometría escolar es obvio que los ángulos $$$\ angle NMP$ y $$$\ angle MAB$ son iguales y, por lo tanto, sus tangentes son iguales:

$$ $$\ tan \ angle MAB = \ tan \ angle NMP = {MB \ over AB} = {NP \ over MP} = {\ Delta y \ over \ Delta x}$$

Añadir a la imagen: $$$MD$ - tangente a la curva inicial en el punto $$$M$ cruza un eje $$$y = 0$ en el punto $$$D$ . Triángulo $$$\ triangle MBD$ - un triángulo rectángulo con hipotenusa - sección de cassette, segmento $$$MD$ .

Apuntamos al incremento $$$\ Delta x$ a cero:

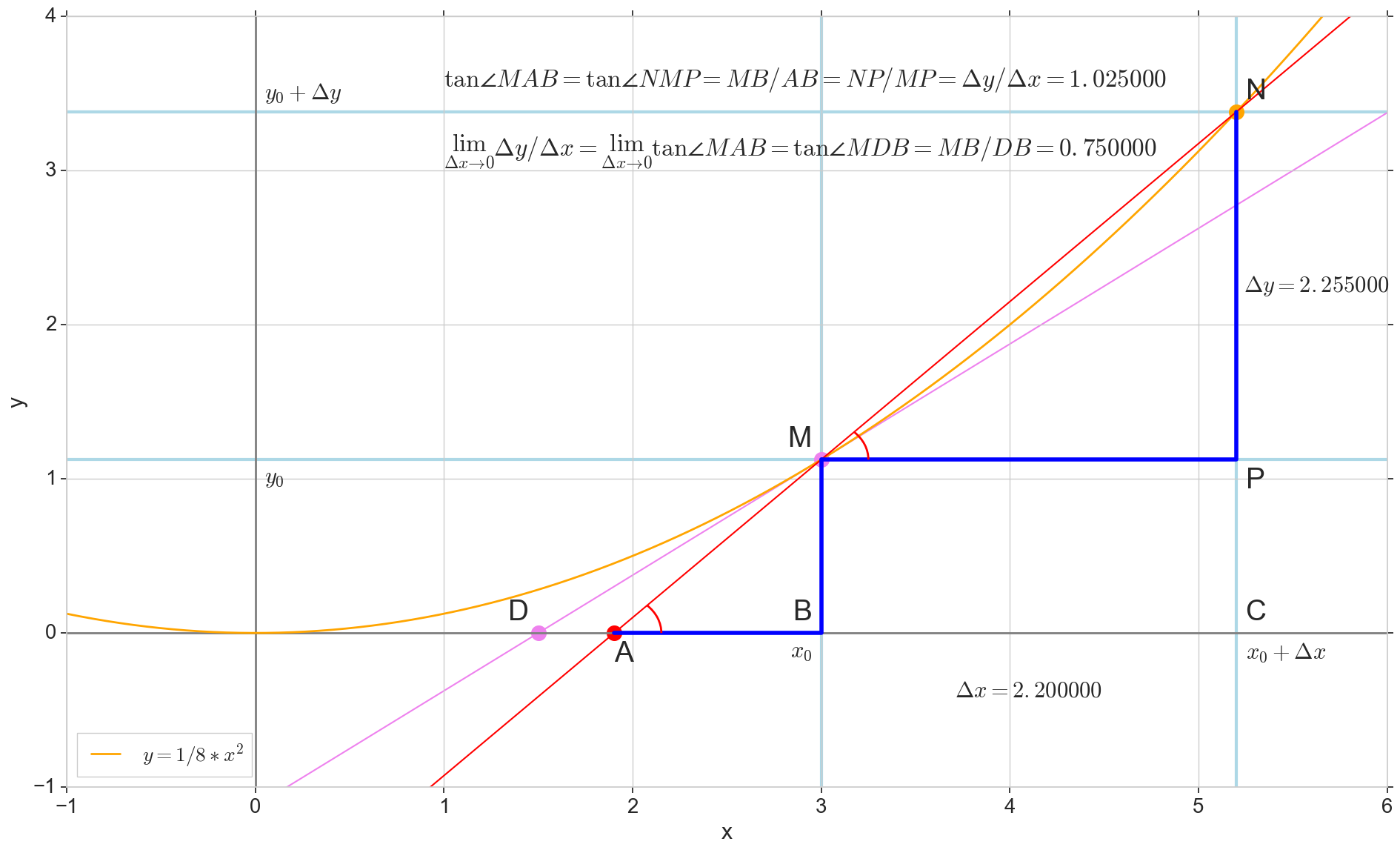
Punto $$$N$ moviéndose al punto $$$M$ por función, punto $$$A$ se arrastra hasta un punto $$$D$ a lo largo del eje $$$y$ secante $$$Mn$ se convierte en una tangente $$$MD$ con punto de contacto $$$M$ . Triángulo fuente $$$\ triangle NPM$ con patas $$$\ Delta x$ y $$$\ Delta y$ se reduce a un punto, pero un triángulo como este $$$\ triangle MBA$ se convierte en un triángulo $$$\ triangle MBD$ preservando no solo las dimensiones macroscópicas, sino también la igualdad de ángulos $$$\ angle MAB$ y $$$\ angle NMP$ .

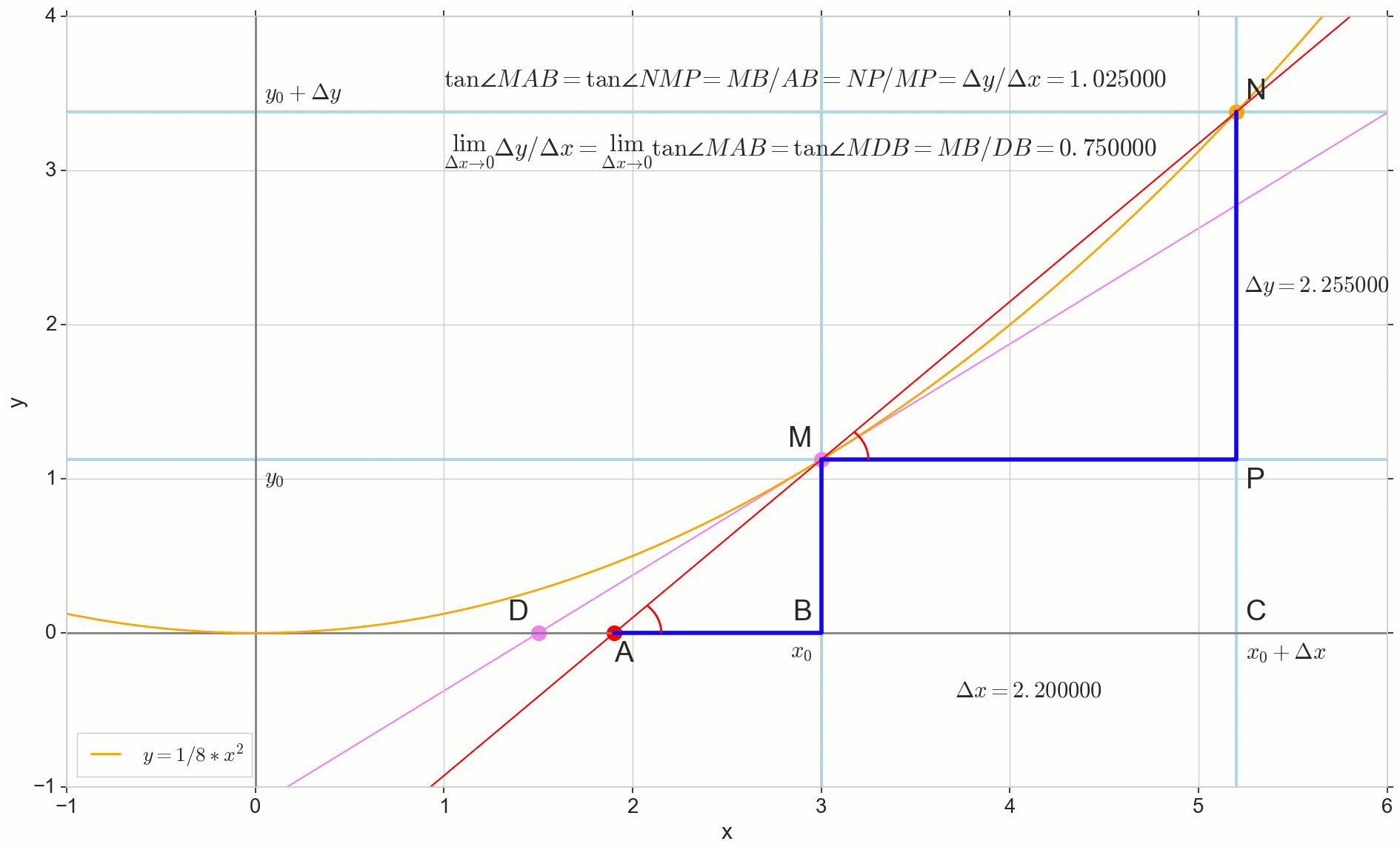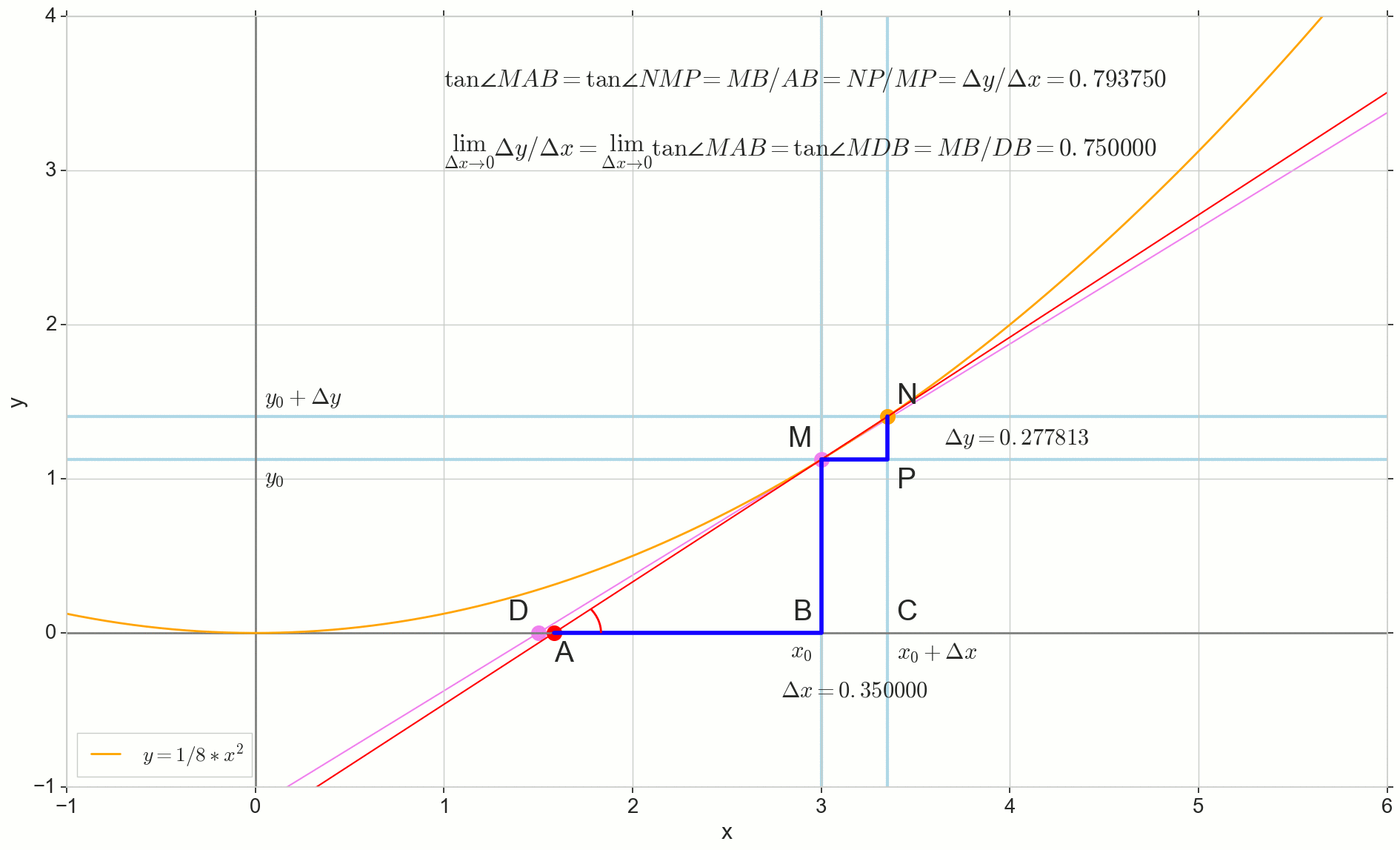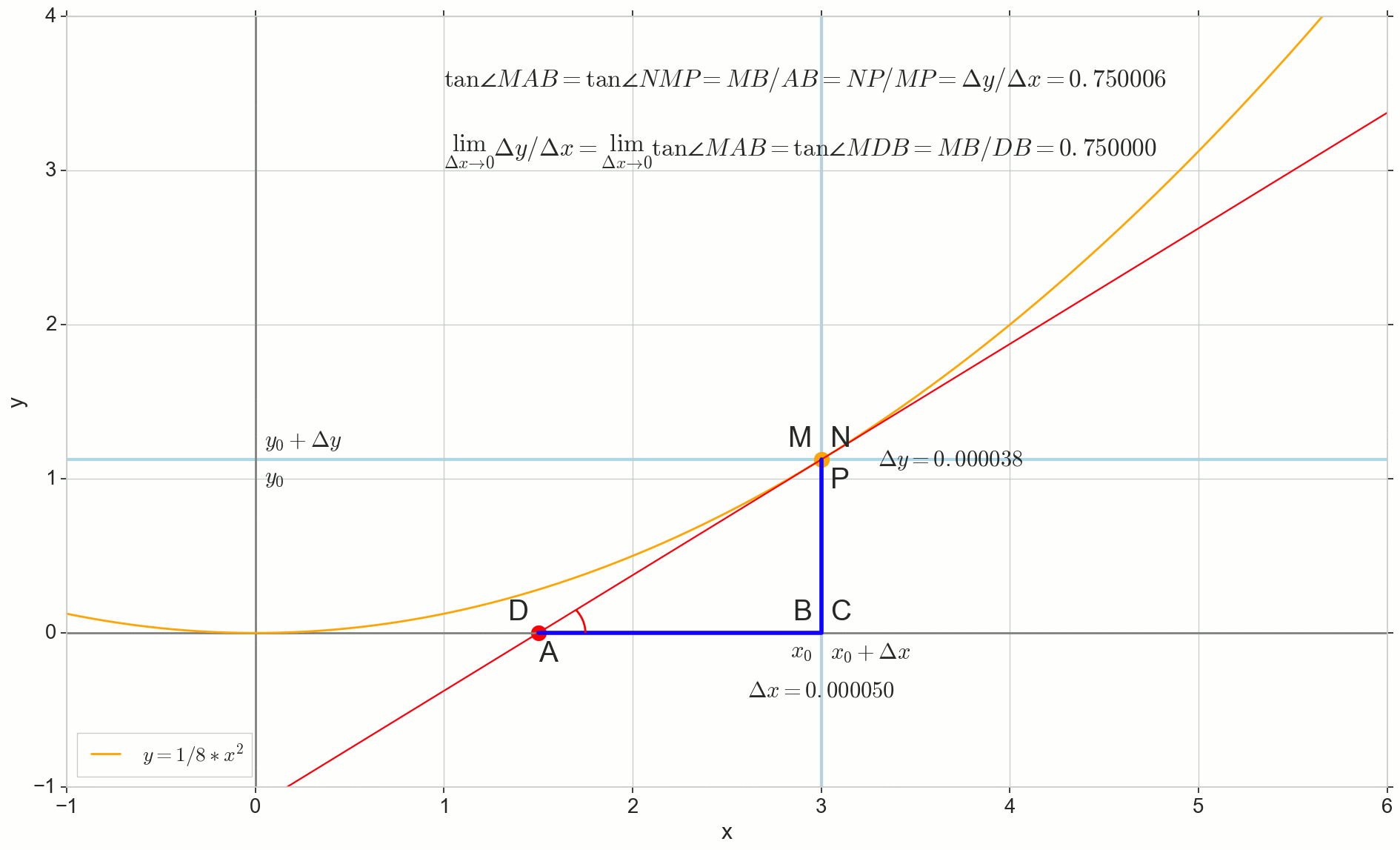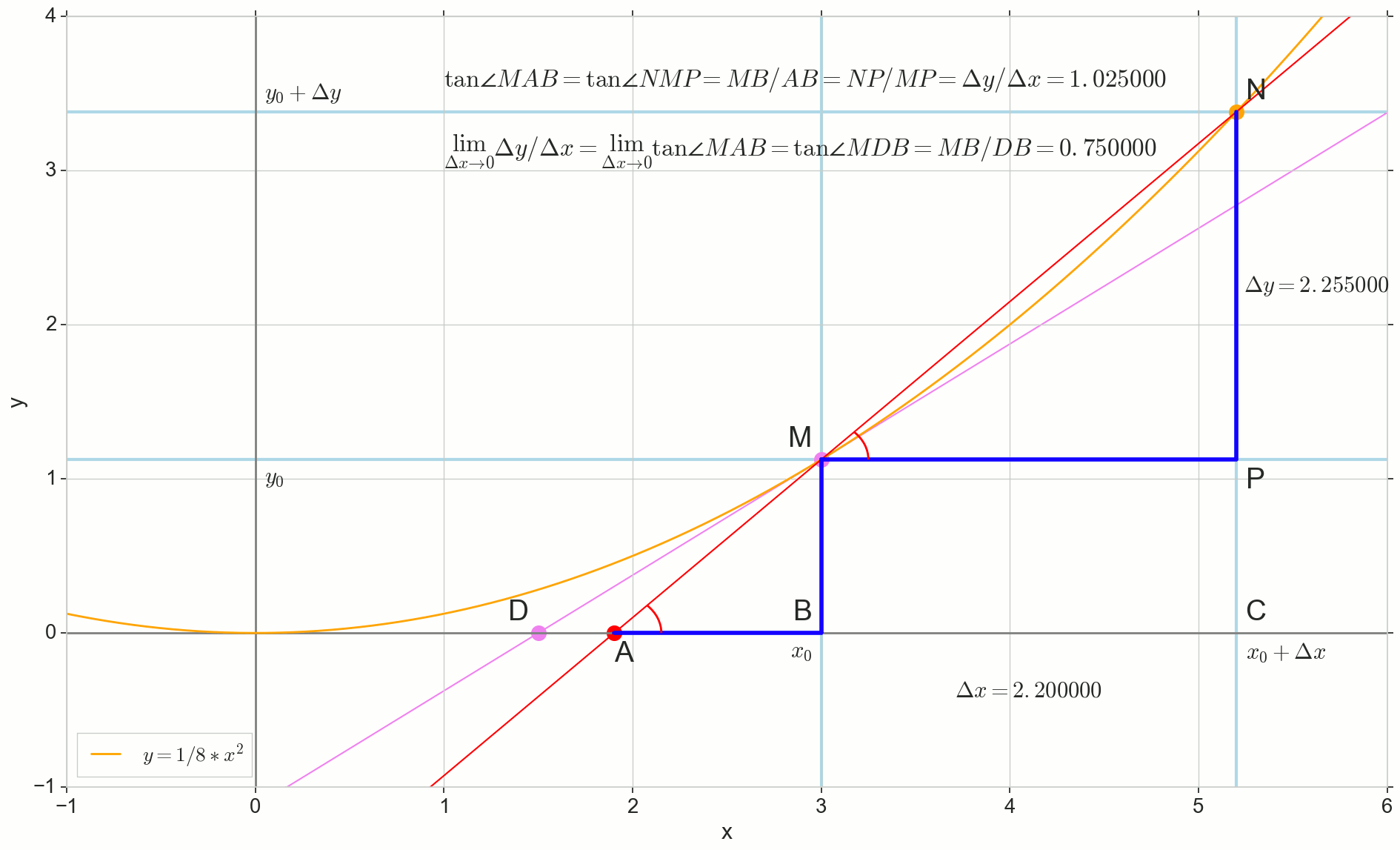
Cómo aumentar $$$\ Delta x$ , infinitamente acercándose a cero, nunca llegará a cero, entonces el punto $$$N$ nunca llegar al lugar exacto $$$M$ punto $$$A$ no llegará al punto $$$D$ triangulo $$$\ triangle MBA$ no se convertirá en $$$\ triangle MBD$ . , , «» $$$\lim$ .

$$$\triangle MBA$ — $$$\triangle MBD$ , :

$$ $$\lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \lim_{\Delta x \to 0}{\tan \angle NMP} = \lim_{\Delta x \to 0}{\tan \angle MAB} = \lim_{\Delta x \to 0}{MB \over AB} = {MB \over DB} = \tan \angle MDB$$

:

$$ $$\lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \tan \angle MDB$$

, , :

$$ $$y'(x_0) = \lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \tan \angle MDB$$

, $$$y=0$ . .

, , , , , . , , , , .. ( , , ). : , (, — tangent line , , — ).

:

• $$$x_0$ $$$y=0$
• — $$$y(x_0)$ — $$$x_0$ $$$y=0$ $$$y=0$
• «» , ,
• — : — , —
• ( , , , $$$\Delta y$ )

, , :

— , — $$$x_0$ , — . — — . — $$$y=0$ , — .

, , , , . ( , ) (: $$$y=0$ , ).

( ): , (: $$$y=0$ , ).

, : (), «»/«» , . — . , , ? .

$$$J(w)$ . , , , .

$$ $$J(w)={1 \over 2} SSE ={1 \over 2}\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2}$$

• $$$k$ -
• ,

$$ $$\begin{gathered}\frac{\partial J(w)}{\partial w_{k}} ={\frac{\partial }{\partial w_{k}}}{1 \over 2}\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} ={1 \over 2}\sum _{i=1}^{n}{\frac{\partial }{\partial w_{k}}}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} \\={1\over 2}\sum _{i=1}^{n}2(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \frac{\partial }{\partial w_{k}}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \\={1\over 2}2\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \frac{\partial }{\partial w_{k}}((w_{0}x_{0}^{(i)}+...+w_{k}x_{k}^{(i)}+...+w_{m}x_{m}^{(i)}) - y^{(i)}) \\=\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})x_{k}^{(i)} \end{gathered}$$

, : , , , ( ) . , $$$w_k$ ( , ), . , , , $$$1/2$ SSE .

:

$$ $$\begin{gathered}\frac{\partial J(w)}{\partial w_{k}} =\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})x_{k}^{(i)} \end{gathered}$$

— ( $$$\nabla$ [], , .. []):

$$ $$\nabla J(w)=(\frac{\partial J(w)}{\partial w_{0}},...,\frac{\partial J(w)}{\partial w_{m}}), w=(w_{0},...,w_{m})$$

:

$$ $$w:=w+\Delta w, \Delta w=-\eta \nabla J(w)$$

$$$k$ - :

$$ $$w_{k}:=w_{k}+\Delta w_{k}, \Delta w_{k}=-\eta \frac{\partial J(w)}{\partial w_{k}}$$

:

• $$$\eta$ [] — ,

, , , . , .

1- :

$$ $$\Phi(x, w)=w_0+w_1x_1$$

( ):

$$ $$\frac{\partial J(w)}{\partial w_{0}} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{0}^{(i)} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})$$

$$ $$\frac{\partial J(w)}{\partial w_{1}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{1}^{(i)}$$

:

$$ $$\Delta w_{0}=-\eta \frac{\partial J(w)}{\partial w_{0}}=-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})$$

$$ $$\Delta w_{1}=-\eta \frac{\partial J(w)}{\partial w_{1}}=-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{1}^{(i)}$$

, . .

( $$$w_1$ )

$$$w_0=1$ , $$$J(w_1)$

$$$X$ ( ) $$$y$ $$$w_0$ y $$$w_1$ ( ):

 def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum() 

$$$w_1$ -1.5 1.5.

  #      w0 = 1 w1 = np.linspace(-1.5, 1.5, 200) #              numpy.dot # https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html #    ,      sse = [] for i in range(len(w1)): sse.append(sse_(X1, y, w0, w1[i])) sse = np.array(sse) 

, ( , , ):

  plt.subplot(3,1,1) # sse plt.plot(w1, sse/2, color='red', label='w0=1') #  -   w1_first = .9 plt.scatter(w1_first, sse_(X1, y, w0, w1_first)/2, color='blue', marker='o', s=100) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'J(w1, w0=1)') plt.legend(loc='lower left') 

, , $$${\delta J(w)} \over {\delta w_1}$ — :

  grad_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() grad_w1.append(grad) plt.subplot(3,1,3) plt.plot(w1, grad_w1, label=u' ∂J(w)/∂w1') plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'∂J(w)/∂w1') plt.legend(loc='upper left') 

$$$\Delta w_1(w_1)$ (, $$$\Delta w_1$ $$$w_1$ , .. , ):

  eta = 0.001 delta_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() delta = -eta*grad delta_w1.append(delta) plt.subplot(3,1,2) plt.plot(w1, delta_w1, color='orange', label=u'Δw1, η=%s'%eta) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'Δw1=-η*∂J(w)/∂w1') plt.legend(loc='upper right') 

  plt.show() 

• : ,
• : — «» ( , «» ),
• : — ( ), $$$\eta$ [] ( ),

: , 1000 .

, ,

$$$w$ — - - . $$$w_0=1$ , $$$w_1=0.9$ . $$$\eta=0.001$ ( , ) 12:

  #    12-14  eta = 0.001 epochs = 12 

:

  #      w1_epochs = [w1_first] delta_w1_epochs = [] w1_next = w1_first for i in range(epochs): grad = ((w0 + w1_next*X1 - y)*X1).sum() delta = -eta*grad w1_next = w1_next + delta delta_w1_epochs.append(delta) w1_epochs.append(w1_next) #   - 0 delta_w1_epochs.append(0) w1_epochs = np.array(w1_epochs) delta_w1_epochs = np.array(delta_w1_epochs) #     sse_epochs = [] for i in range(len(w1_epochs)): sse_epochs.append(sse_(X1, y, w0, w1_epochs[i])) sse_epochs = np.array(sse_epochs) 

$$$w_1$ $$$J(w_1, w_0=1)$ :

  #     -       size_epochs = [10 + (250-100)*epoch/epochs for epoch in reversed(range(epochs+1))] plt.scatter(w1_epochs, sse_epochs/2, color='blue', marker='o', s=size_epochs, label=u'  , η=%s'%eta) #    w1 plt.plot([w1_epochs, w1_epochs+delta_w1_epochs], [sse_epochs/2, sse_epochs/2], color='orange')#, label='Δw1') 

$$$\Delta w_1(w_1)$

 plt.scatter(w1_epochs, delta_w1_epochs, color='blue', marker='o', s=size_epochs, label=u'  , η=%s'%eta) plt.plot([w1_epochs, w1_epochs], [delta_w1_epochs, np.zeros(len(delta_w1_epochs))], color='orange') 

, , ( ), . , , , .

: , , , «» , — , .

• — $$$w_1$ , —
• , $$$w_1$
• — : , —
• , —
• , ( ), , ( ) — , —
• ( , — ).
• : — , —
• ? — . .
• . $$$w_1$ , . , «»/«» . , , . , , , « ». , : $$$w_1=0.9$ 200, , , , 1. , , , . — $$$\eta$ . , 200 1. $$$\eta=0.001$ , $$$w_1=0.9$ 200*0.001=0.2 ( -1, -0.2) — .
• $$$J(w_1=0.9)=92.43$ , 12 (, ) $$$J(w_1=0.03)=8.54$
• , ,

, . , . , ( , ). $$$\eta$ , .

: , , , .

, , , .

$$$\eta$

• $$$\eta$ [] — ()
• ,
• «»: , , ,
• , $$$J(w)$
• : $$$w_k$ , $$$\eta$ , $$$w_k$

$$$\eta=0.01$

 #    eta = 0.01 epochs = 6 

. , . 3- , 3- , , .. , .. . , , [] .

$$$\eta$ $$$J(w)$ $$$\eta$

  #      J(w0, w1)   w0  w1 #    12-14  eta = 0.001 epochs = 12 #  -   #   w0  w1 -  ,   , #    10-15  # NB: (    , , ,  , #      ) w0_first = -.9 w1_first = -.9 #      w0_epochs = [w0_first] w1_epochs = [w1_first] delta_w0_epochs = [] delta_w1_epochs = [] w0_next = w0_first w1_next = w1_first for i in range(epochs): grad_w0 = (w0_next + w1_next*X1 - y).sum() delta_w0 = -eta*grad_w0 grad_w1 = ((w0_next + w1_next*X1 - y)*X1).sum() delta_w1 = -eta*grad_w1 w0_next = w0_next + delta_w0 w1_next = w1_next + delta_w1 delta_w0_epochs.append(delta_w0) delta_w1_epochs.append(delta_w1) w0_epochs.append(w0_next) w1_epochs.append(w1_next) #     sse_epochs = [] for i in range(len(w1_epochs)): sse = sse_(X1, y, w0_epochs[i], w1_epochs[i]) sse_epochs.append(sse) print('epoch=%d, w0=%f, w1=%f, SSE/2=%f' % (i, w0_epochs[i], w1_epochs[i], sse/2)) sse_epochs = np.array(sse_epochs) #  -      η (--) plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, η=%s'%eta) plt.xlabel(u'epoch (η=%s)'%eta) plt.ylabel(u'J(w)') plt.legend(loc='upper right') plt.show() 

: , , . , — , , .

:

 #   eta = 0.001 epochs = 50 

:

 #    eta = 0.01 epochs = 8 

.

$$$\eta$ . , , .

, .

:

• : , , ( ). , , , , .
• : .

, ( ) $$$w$ , , . , , , . , , .

,

, .

, :

— :

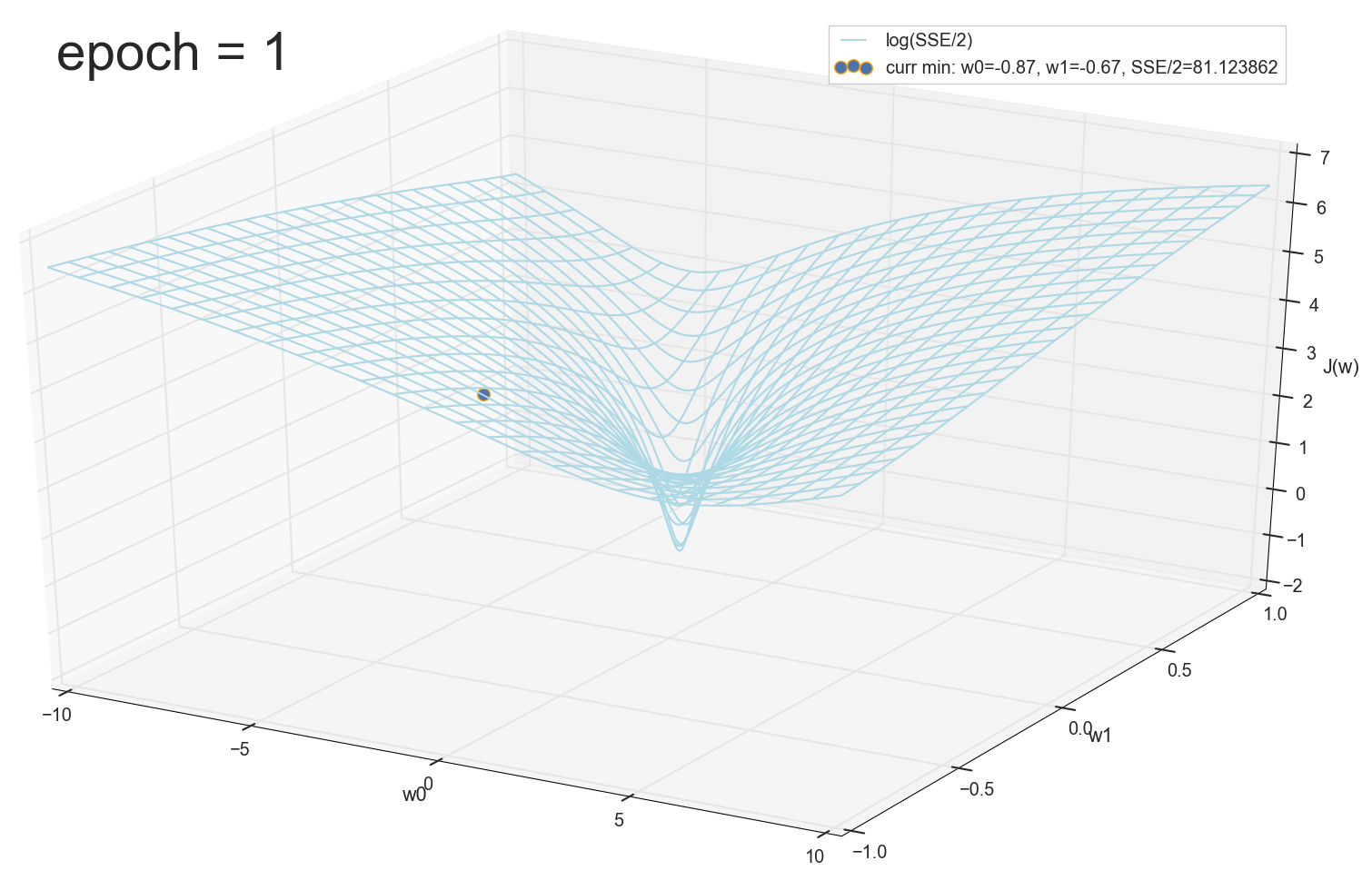
12 — , :

50 :

1767 — , :

, 62000 :

:

. , : , , . , , , , , , . , , - .

, , - , - : , , , , , — . , , , , , , , — . ?

, . :

, , ( ). : , . , , .

. , .

. , , . , — .

— :

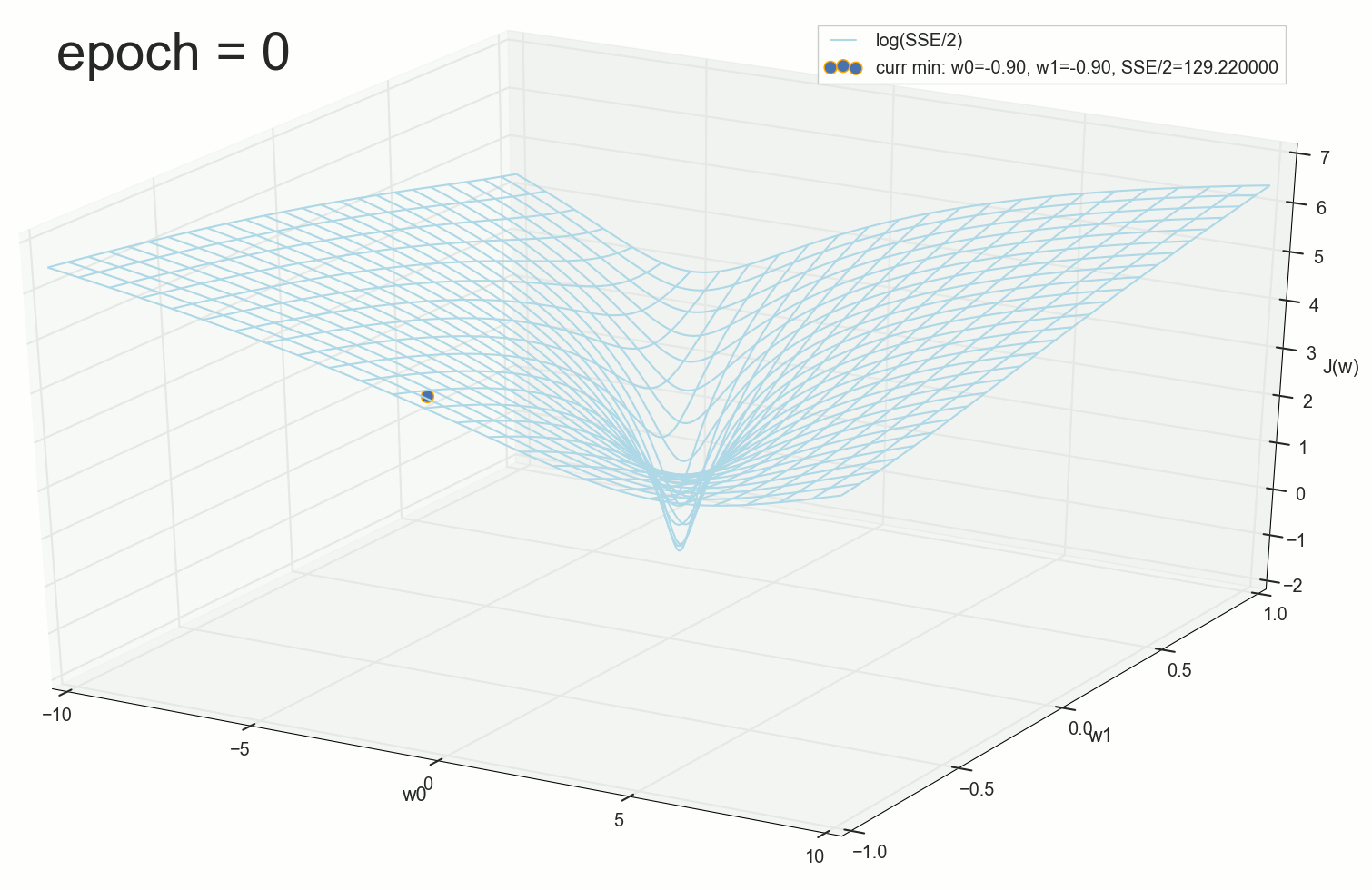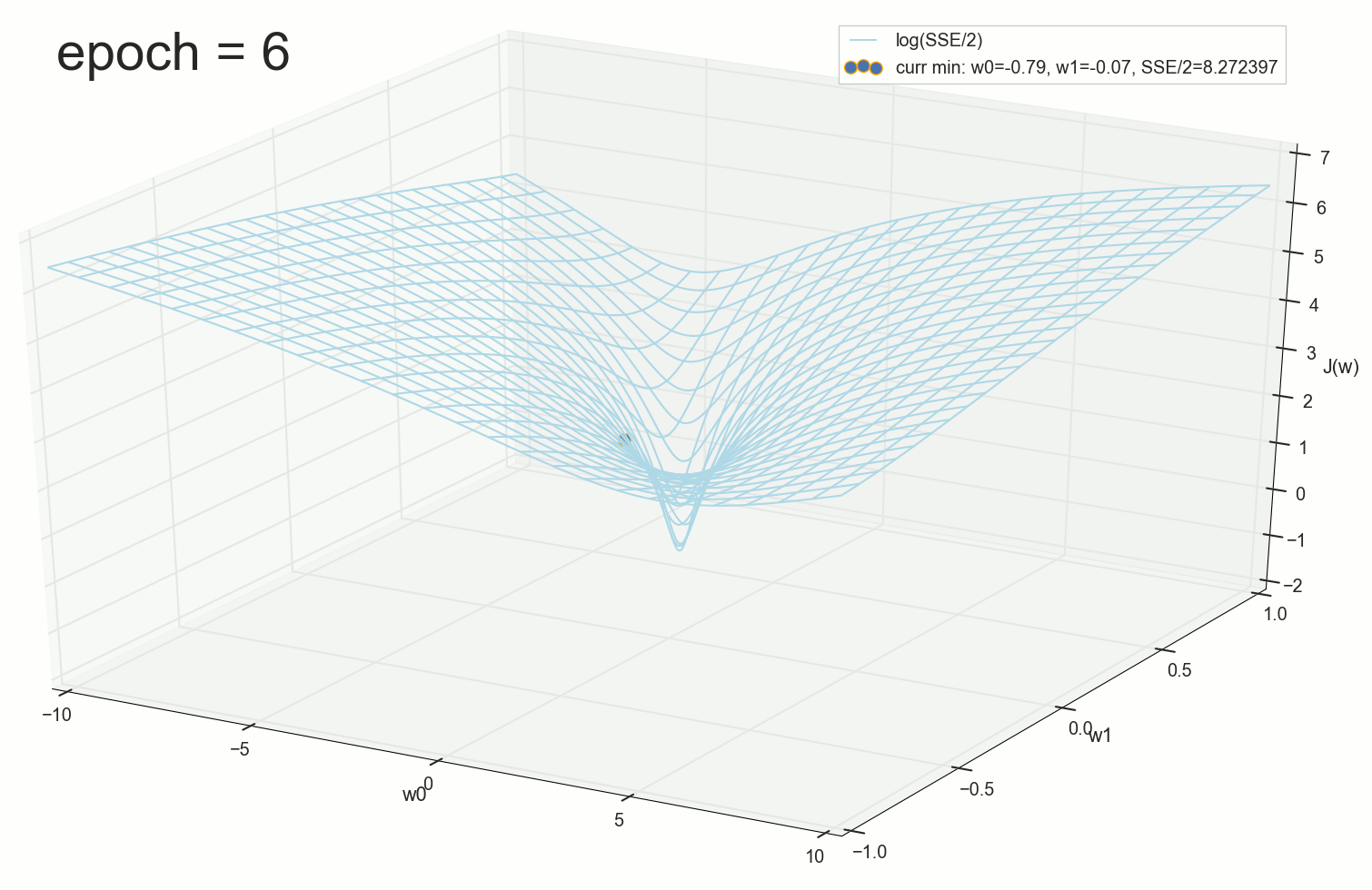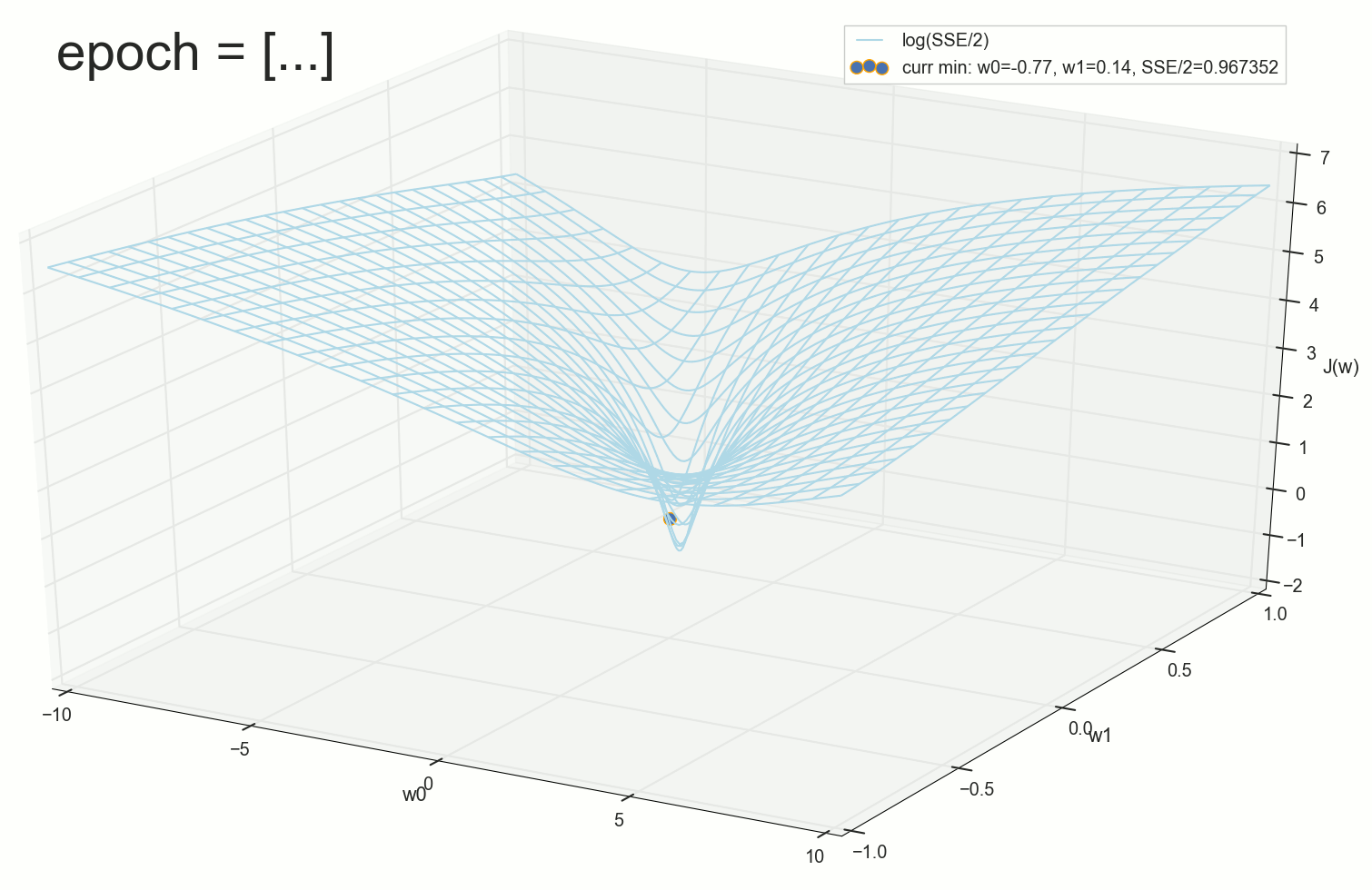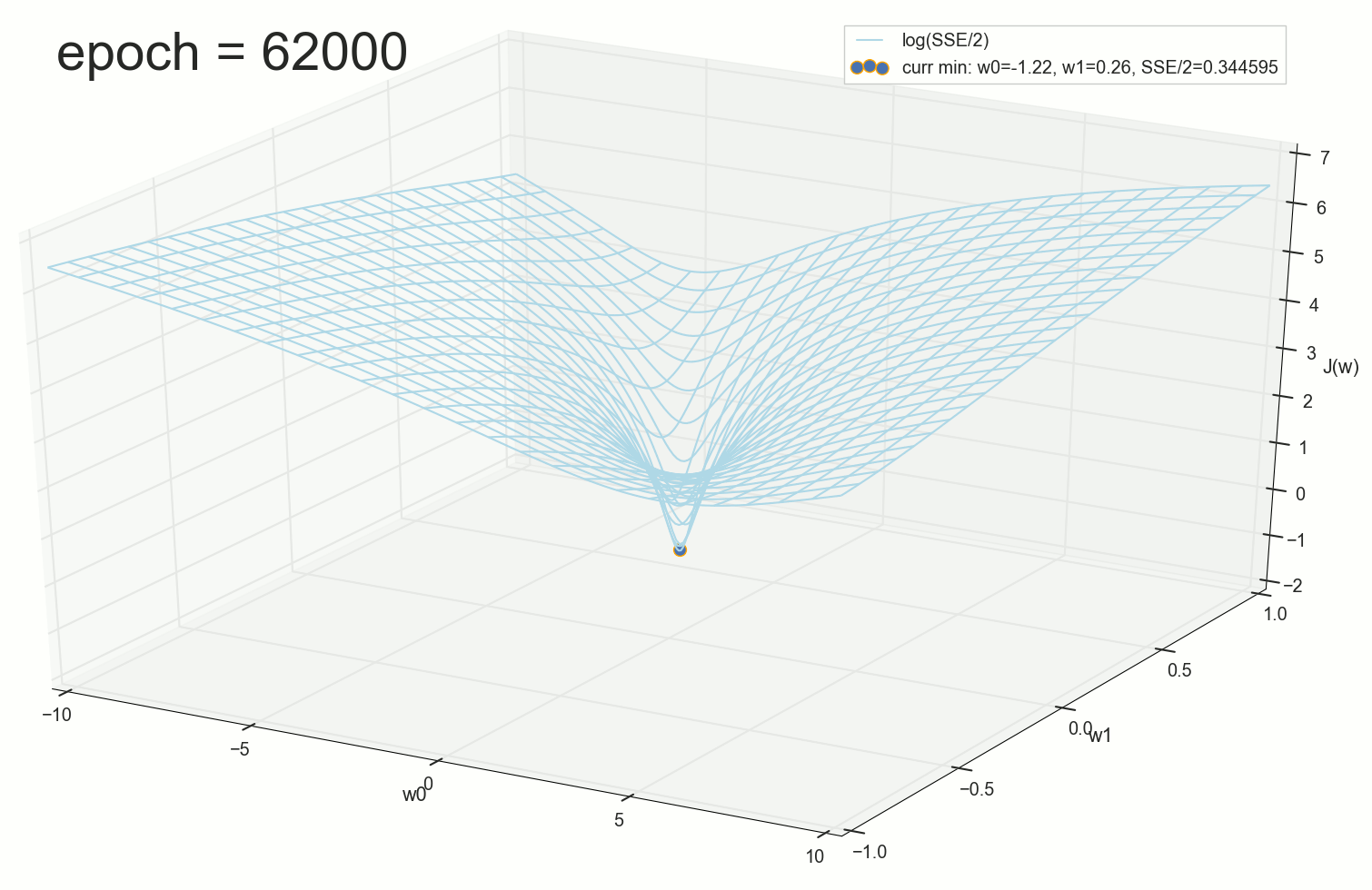
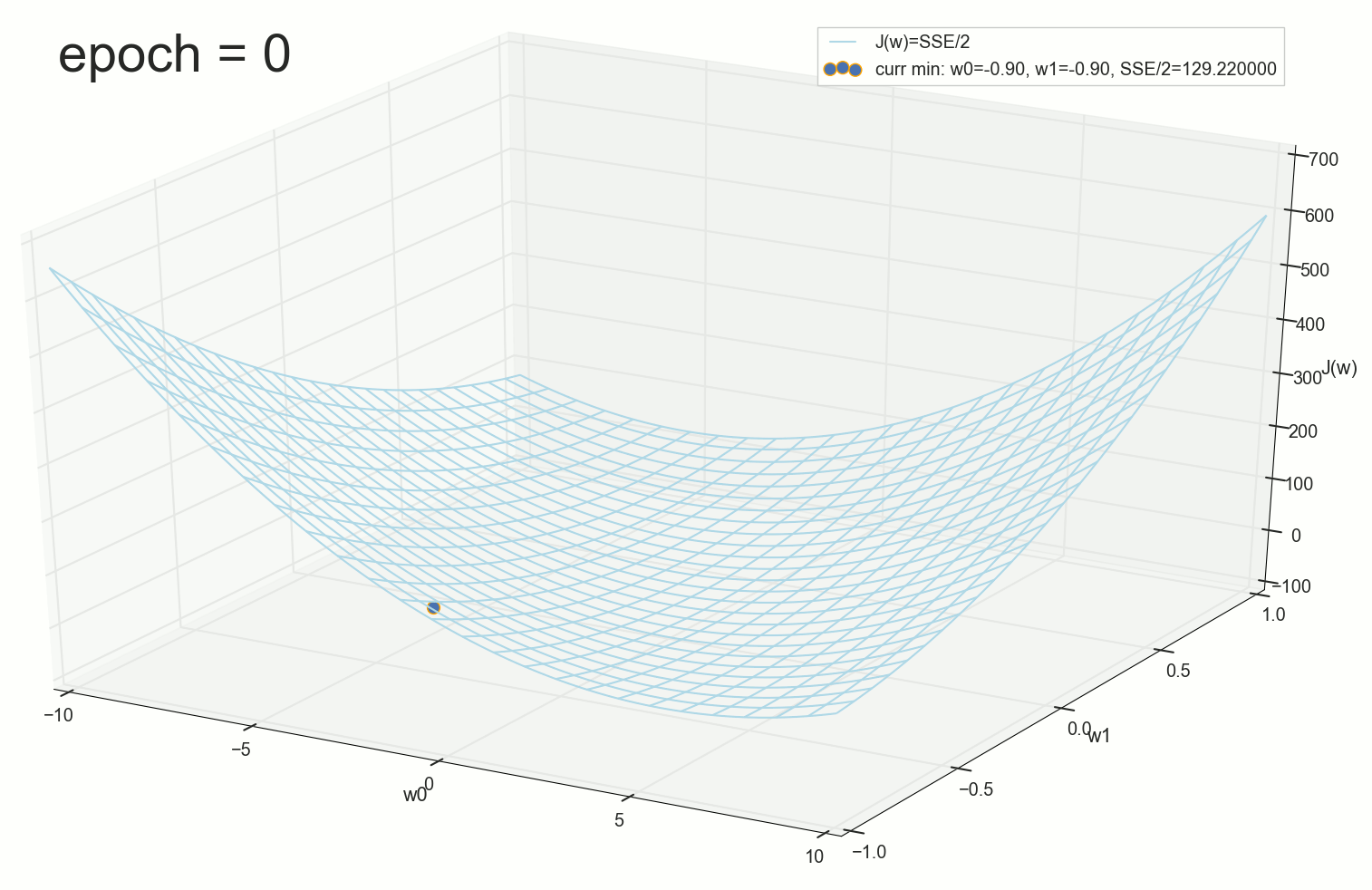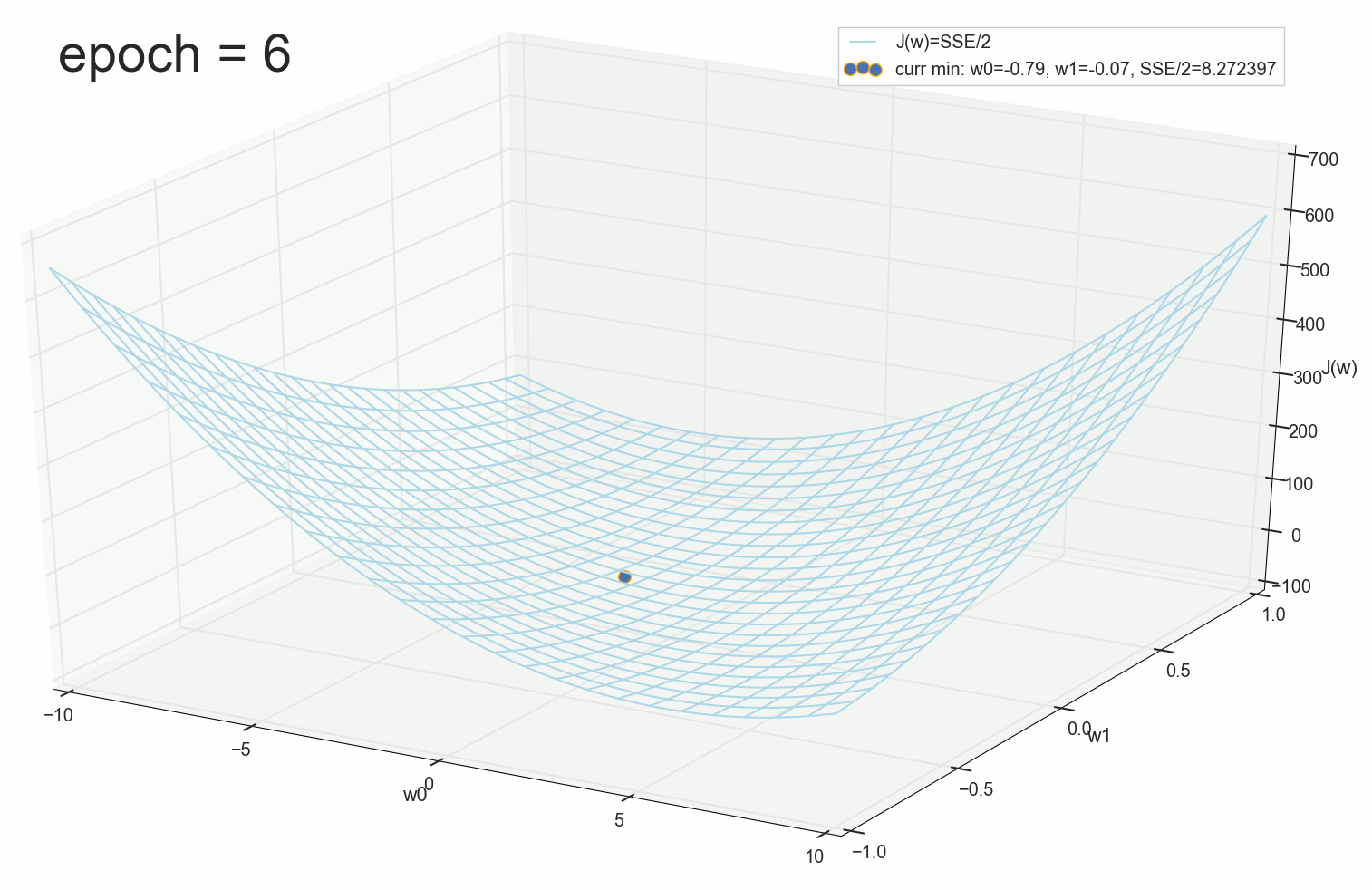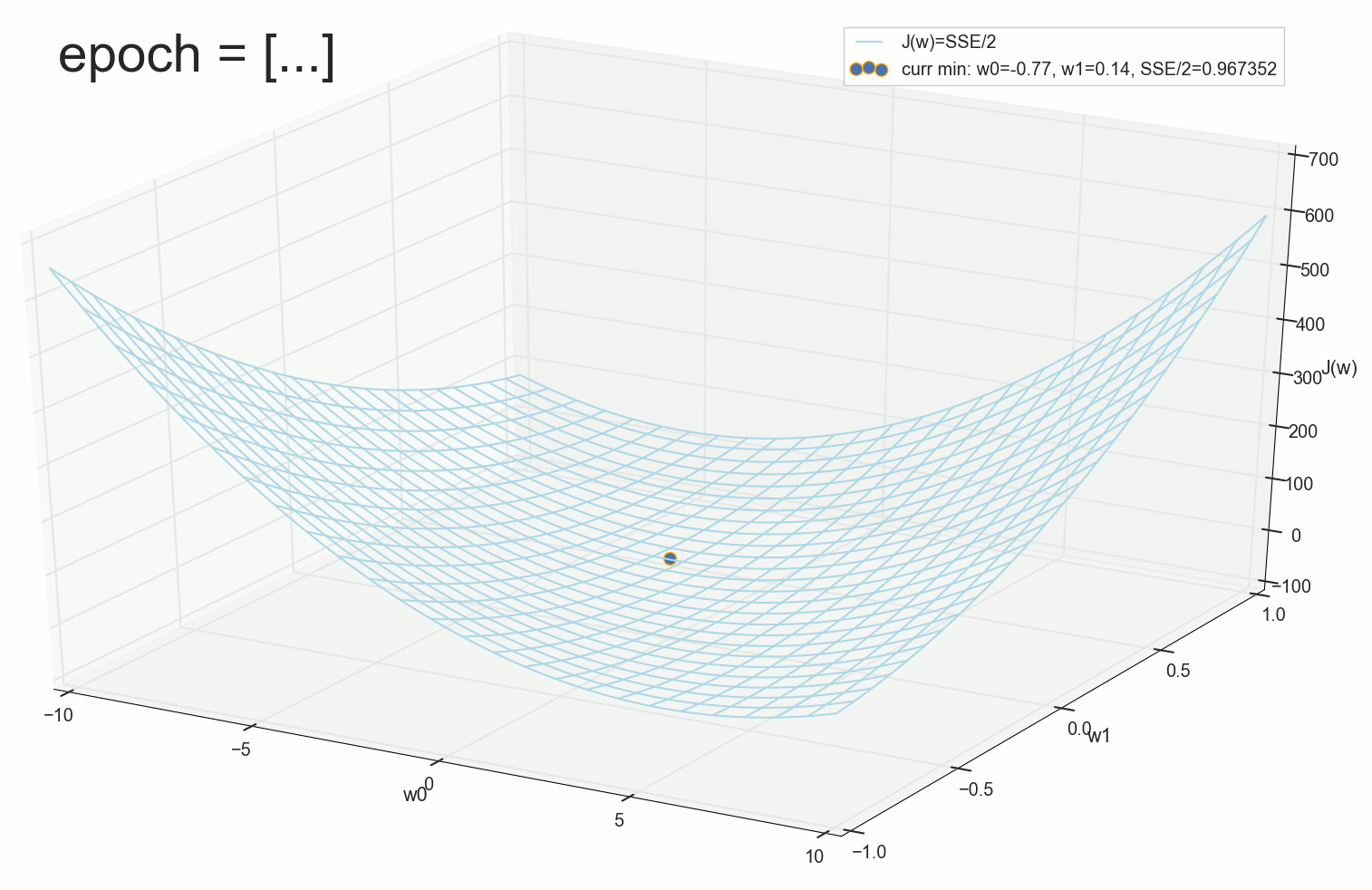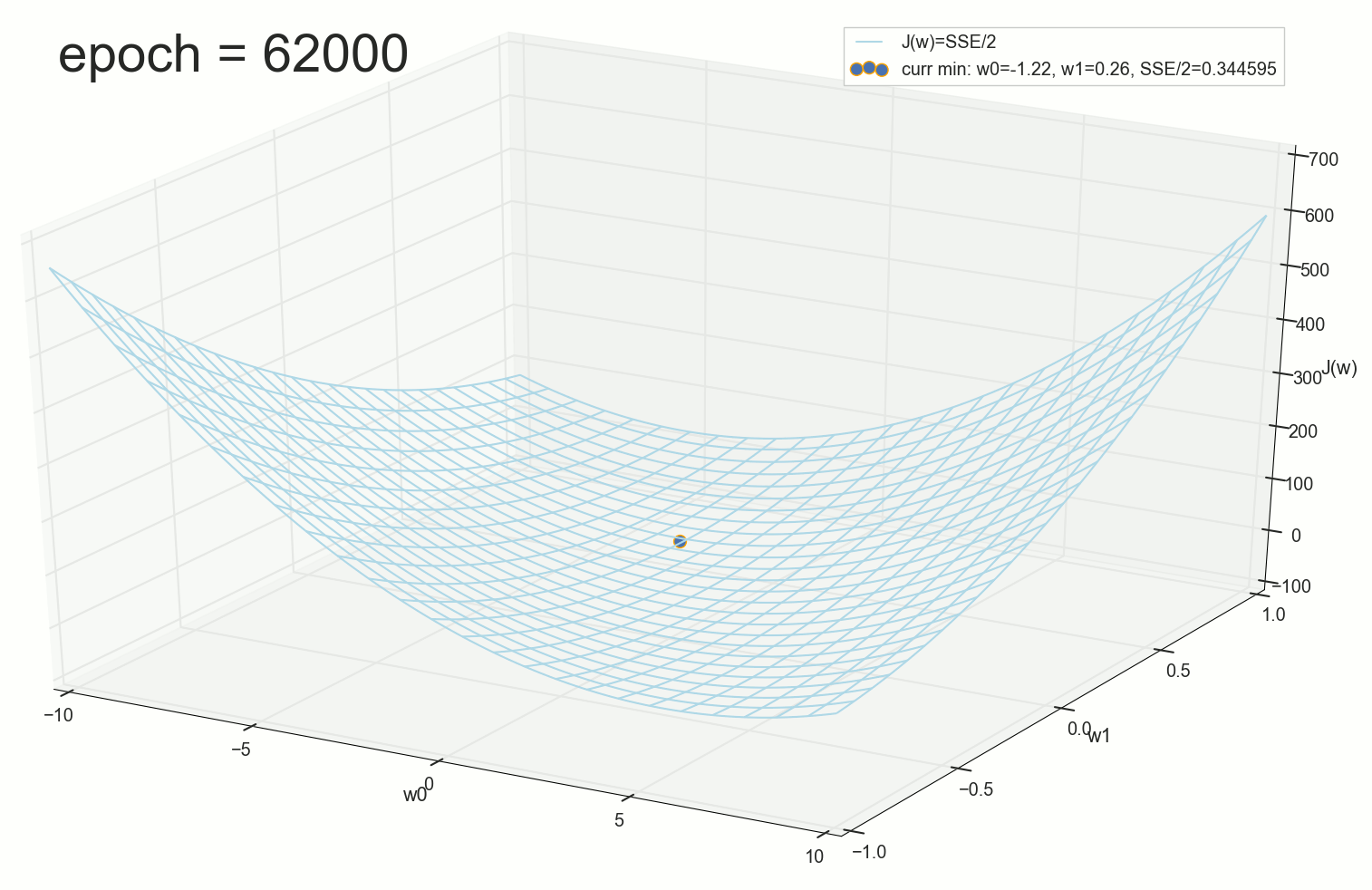
11- : , ; :

12- : , , :

50- : , 12-

1766: . $$$J(w)=0.3456480221$ — , , ( $$$J(w)=0.3456478372$ : 6- , , )

1767: $$$J(w)=0.34564503$ — , ( 6- , ). $$$w_0=-1.184831$ , $$$w_1=0.258455$ ( $$$w_0$ 2- : $$$w_0=-1.27$ , $$$w_1=0.26$ )

62000: $$$J(w)=0.3445945$ — , ( 2- ). :

:

. , , , , .

• $$$\eta=0.001$ , 10-12- ( )
• , , , (1767)
• — 60
• —

— ( , 1767): $$$w_0=-1.184831$ , $$$w_1=0.258455$ .

.

$$$t^{(1)}=(t_1^{(1)})=(1.4)$ ( , $$$t^{(i)}$ — ). , .. , , $$$\hat y=-1$ , .. .

$$ $$SUM=w_0 + w_1*t_1^{(1)} = -1.18 + 0.26*1.4=-0.816$$

$$ $$\Phi(SUM)=SUM=-0.816$$

$$ $$\Phi(SUM)=-0.816 < 0 \implies \hat y = -1$$

, .

: $$$t^{(2)}=(t_1^{(2)})=(7)$

$$ $$\Phi(SUM)=SUM= -1.18 + 0.26*7 = 0.64 \geqslant 0 \implies \hat y = 1$$

$$$\hat y = 1$, .. . .

, ( «» ) 12 . , !

(m=2)

, , , . . , , .

— ( ). 2- .

• $$$x = (x_1, x_2)$( , , )
• $$$y = \{-1, 1\}$( , )

 #  -  ( ) X1 = np.array([2, 3, 1, 5, 10, 1, 6, 7, 10, 6, 7]) X2 = np.array([1, 1, 2, 2, 3, 5, 6, 6, 7, 8, 8]) #   -   y = np.array([-1, -1, -1, -1, 1, -1, 1, 1, 1, 1, 1]) 

 plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u': -1') plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u': 1') #    #  - -  w0 = -2.7 w1 = .3 w2 = .4 #   ( ) -      =0: # 0=w0+w1*X1+w2*X2 # X2=-(w0+w1*X1)/w2 plt.plot(np.linspace(0,12), -(w0+w1*np.linspace(0,12))/w2, label=u' ') plt.xlim(0, 11) plt.ylim(0, 9) plt.legend(loc='upper left') plt.xlabel('X1') plt.ylabel('X2') plt.show() 

, .

$$ $$\Phi(x, w) = w_0 + w_1 x_1 + w_2 x_2$$

, — , , 1- , 3-:

:

:

— :

() $$$\Phi(w) = 0$(-). :

, , , , , ( , ). , . , , m=2, (m+1)=3: , — , , — , ( ).

$$ $$J(w)={1 \over 2} SSE = {1 \over 2}\sum_{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)} + w_{2}x_{2}^{(i)} - y^{(i)})^{2}$$

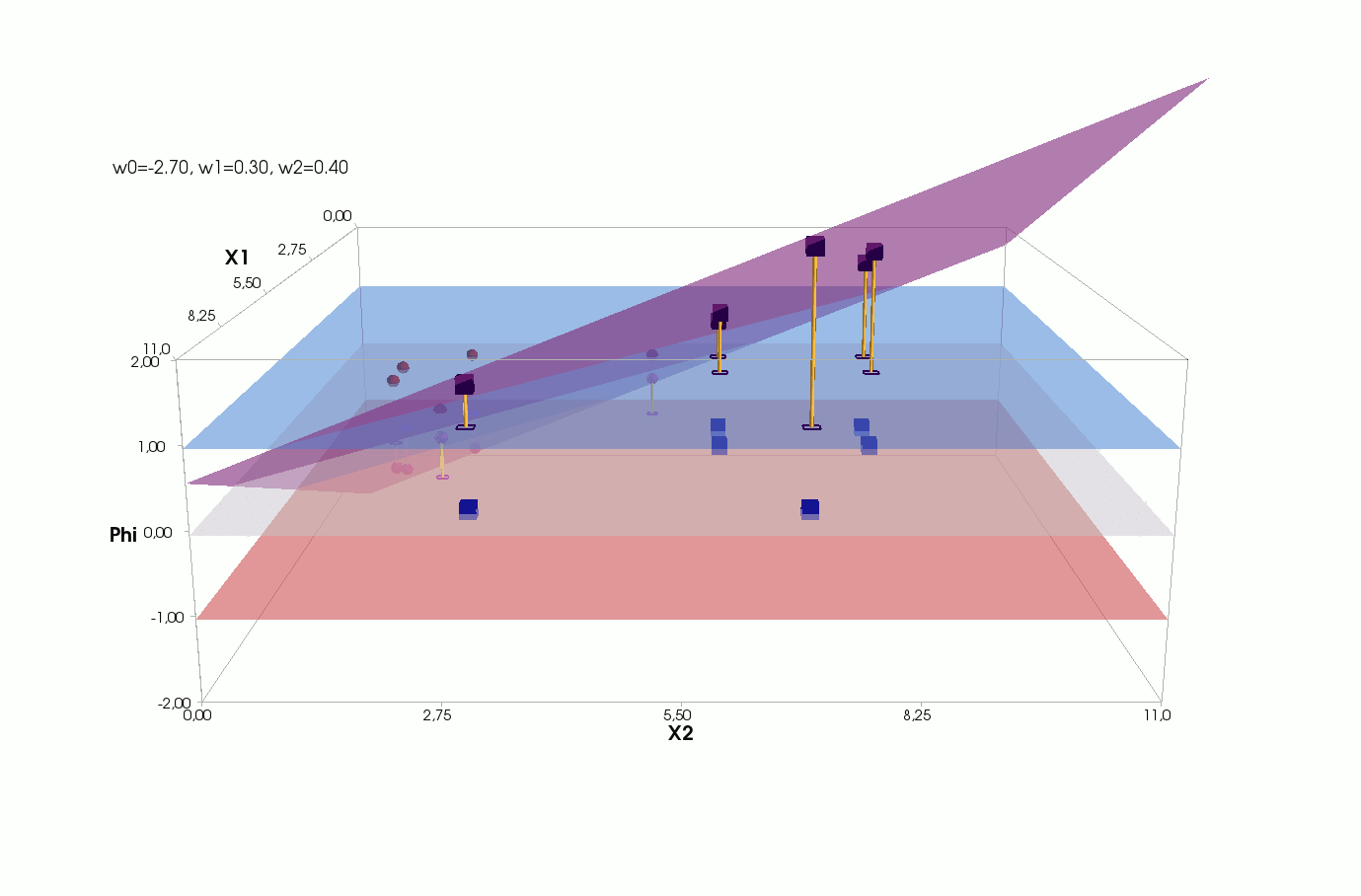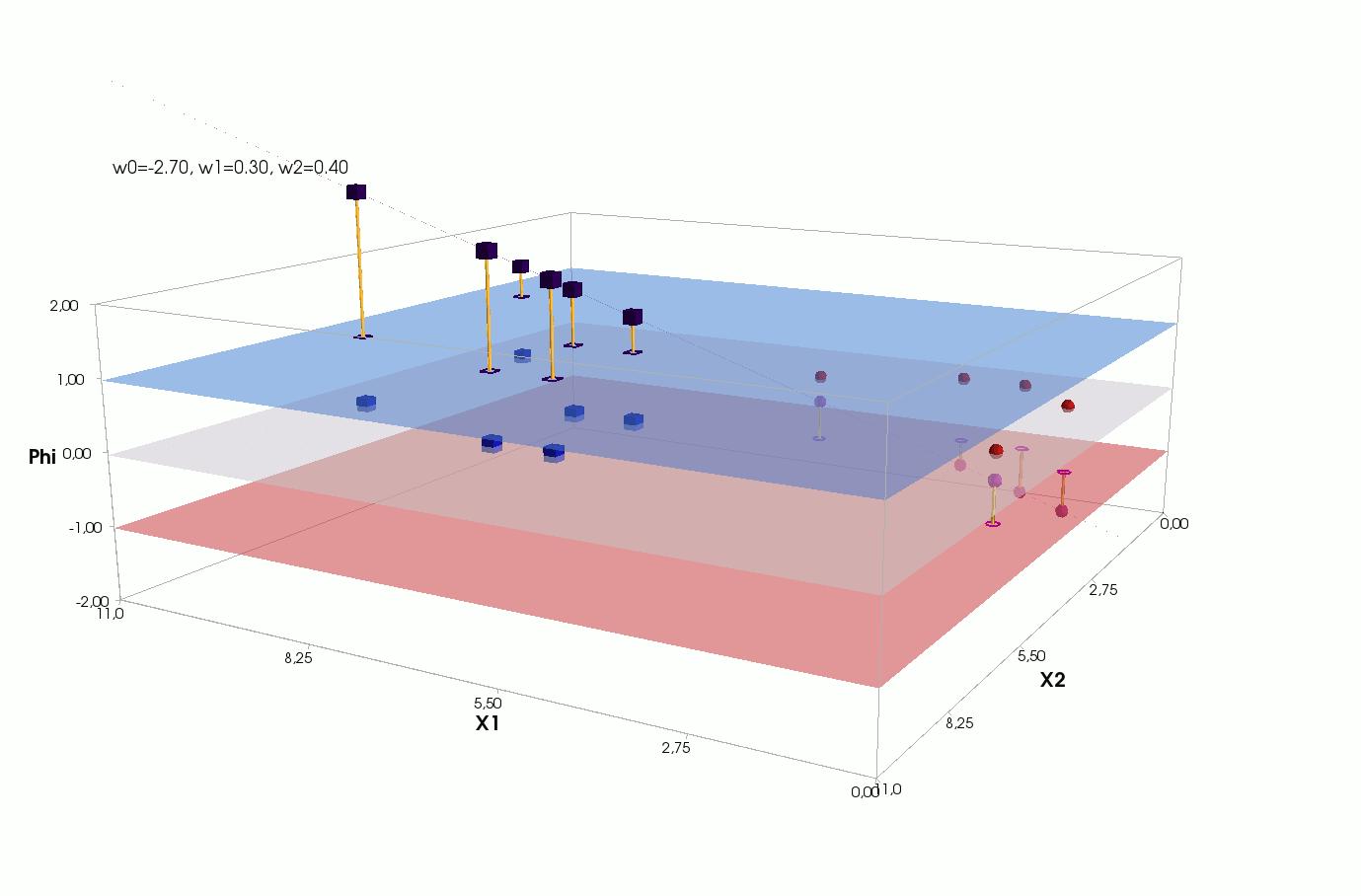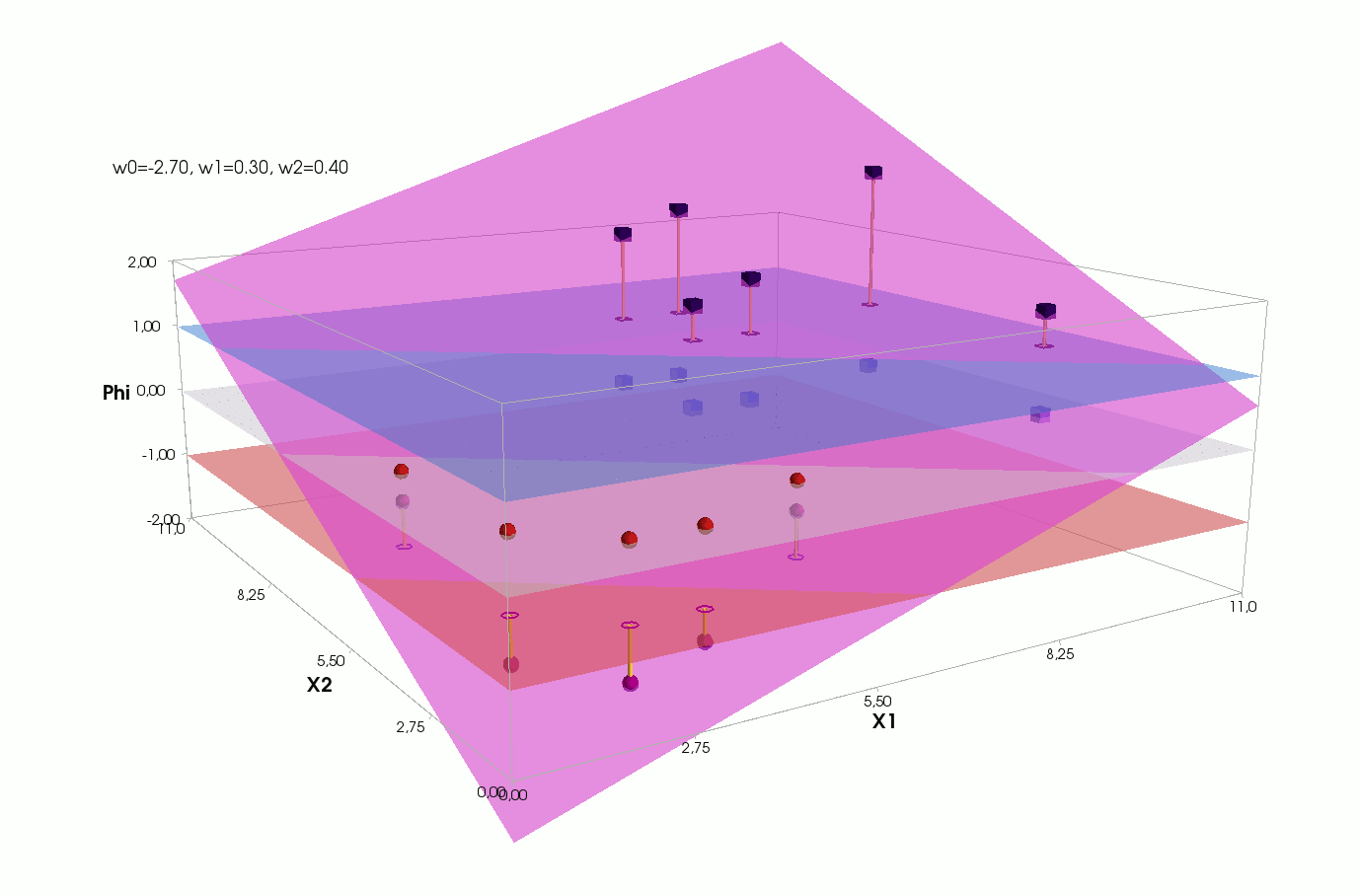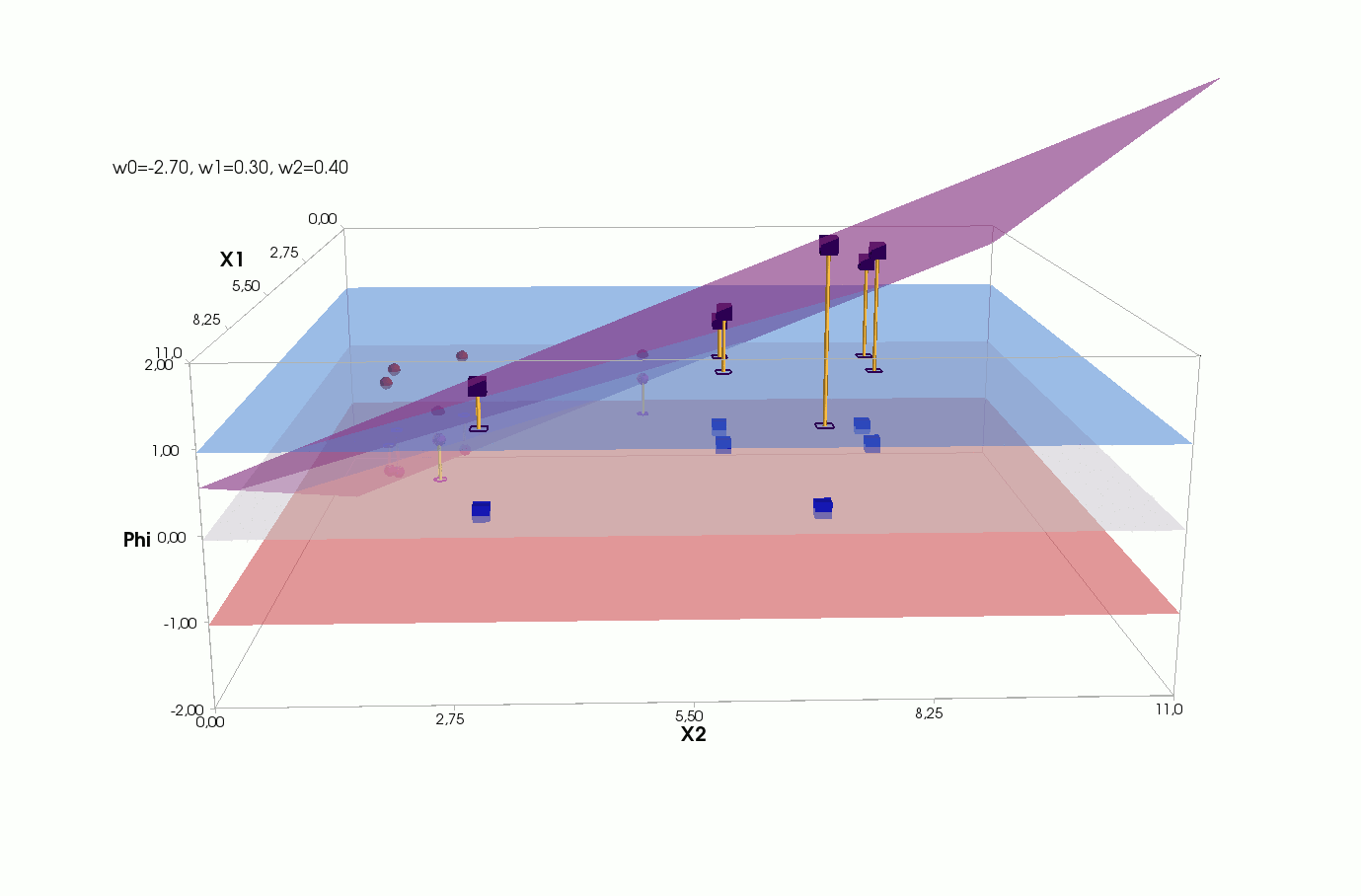
() , .., , 3 + — 4 . , 2- 3- - 3-, , - 4- 3-, .

2- . , , 1- 2-.

$$ $$\nabla J(w)=(\frac{\partial J(w)}{\partial w_{0}}, \frac{\partial J(w)}{\partial w_{1}}, \frac{\partial J(w)}{\partial w_{1}}), w=(w_{0}, w_{1}, w_{2})$$

( ):

$$ $$\frac{\partial J(w)}{\partial w_{0}} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})$$

$$ $$\frac{\partial J(w)}{\partial w_{1}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{1}^{(i)}$$

$$ $$\frac{\partial J(w)}{\partial w_{2}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{2}^{(i)}$$

:

$$ $$\Delta w_{0}=-\eta \frac{\partial J(w)}{\partial w_{0}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})$$

$$ $$\Delta w_{1}=-\eta \frac{\partial J(w)}{\partial w_{1}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{1}^{(i)}$$

$$ $$\Delta w_{2}=-\eta \frac{\partial J(w)}{\partial w_{2}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{2}^{(i)}$$

3- ( 3- ), $$$\eta=0.001$, $$$w_0=-0.9$, $$$w_1=-0.9$, $$$w_2=-0.9$.

— , , :

:

:

3- - :

4- :

60- — , :

70- , , :

200- — :

400- — :

:

, , $$$w_0$.

Código

matplotlib ( mpl_toolkits.mplot3d.axis3d) ( , , 3). Mayavi .

 import numpy from mayavi import mlab #    -   mlab.savefig #mlab.options.offscreen = True #   size    mlab.savefig fig = mlab.figure(fgcolor=(10./256., 10./256., 10./256.), bgcolor=(255./256., 255./256., 255./256.), size=(1650, 950)) X1_ = range(0, 12) X2_ = range(0, 12) XX1_, XX2_ = np.mgrid[X1_, X2_] #    # : color=(255./256., 191./256., 71./256.) # : color=(171./256., 0./256., 130./256.) # : color=(255./256., 101./256., 107./256.) # : color=(252./256., 79./256., 245./256.) # : color=(84./256., 148./256., 247./256.) # : color=(45./256., 0./256., 82./256.) # : color=(254./256., 255./256., 87./256.) #  # : color=(.7, .1, .1) # : color=(.1, .1, .7) #   : =1 (y=1), =-1 (y=-1)    =0 mlab.surf(XX1_, XX2_, np.full((12, 12), -1), color=(255./256., 101./256., 107./256.), opacity=0.6) mlab.surf(XX1_, XX2_, np.full((12, 12), 1), color=(84./256., 148./256., 247./256.), opacity=0.5) mlab.surf(XX1_, XX2_, np.full((12, 12), 0), color=(247./256., 243./256., 246./256.), opacity=0.5) #     # (   , ..      ,   #     :    2- , 3  - #   ,   ) mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, 0), color=(.7, .1, .1), mode='sphere', scale_factor=.2) mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 0), color=(.1, .1, .7), mode='cube', scale_factor=.2) #     mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, -1), color=(171./256., 0./256., 130./256.), mode='2dcircle', scale_factor=.2) mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 1), color=(45./256., 0./256., 82./256.), mode='2dsquare', scale_factor=.2) #    #      # ... epoch=12 w0=-0.762718 w1=0.165023 w2=0.040271 sse=3.598883 #  -   y=w0+w1*X1+w2*X2 yy_ = w0 + w1*XX1_ + w2*XX2_ actsurf = mlab.surf(XX1_, XX2_, yy_, color=(252./256., 79./256., 245./256.), opacity = 0.6) #       y_ = w0 + w1*X1 + w2*X2 mlab.points3d(X1[y==-1], X2[y==-1], y_[y==-1], color=(171./256., 0./256., 130./256.), mode='sphere', scale_factor=.2) mlab.points3d(X1[y==1], X2[y==1], y_[y==1], color=(45./256., 0./256., 82./256.), mode='cube', scale_factor=.2) #   -       #      for i in range(len(X1[y==-1])): mlab.plot3d( [X1[y==-1][i], X1[y==-1][i]], [X2[y==-1][i], X2[y==-1][i]], [y[y==-1][i], y_[y==-1][i]], color=(255./256., 191./256., 71./256.)) for i in range(len(X1[y==1])): mlab.plot3d( [X1[y==1][i], X1[y==1][i]], [X2[y==1][i], X2[y==1][i]], [y[y==1][i], y_[y==1][i]], color=(255./256., 191./256., 71./256.)) #   -       # (      ) zmin=-2. zmax=2. vis_area = mlab.points3d( [np.min(X1_), np.max(X1_)], [np.min(X2_), np.max(X2_)], [zmin, zmax], mode='point') #          mlab.view( focalpoint=((np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2), distance=25, azimuth=-50, elevation=75) mlab.move((0,0,10)) #           fig.scene.renderer.use_depth_peeling = 1 #  mlab.outline(vis_area, color=(.7, .7, .7)) #   ,      : -2, -1, 0, 1, 2 axes = mlab.axes(vis_area, nb_labels=5, color=(.7, .7, .7), ranges=[np.min(X1_), np.max(X1_), np.min(X2_), np.max(X2_), zmin, zmax], #xlabel=u'X1', ylabel=u'X2', zlabel=u'(SUM) - ') xlabel=u'X1', ylabel=u'X2', zlabel=u'Phi') #      #from pprint import pprint #pprint(vars(axes)) axes._label_text_property.bold = False axes._label_text_property.italic = False axes._title_text_property.bold = True axes._title_text_property.italic = False #  ,     #axes._title_text_property.font_size = 34 #         : axes.axes.font_factor = .7 #       size  mlab.figure, #        title = mlab.title("epoch=" + str(epoch)) title.actor.text_scale_mode='none' title.property.justification='right' title.property.font_size=48 legend = mlab.text(.6, .8, 'w0=%0.2f, w1=%0.2f, w2=%0.2f, sse/2=%0.6f'%(w0, w1, w2, sse/2)) legend.actor.text_scale_mode='none' legend.property.font_size=18 #   mlab.show() #    #mlab.savefig("epoch" + str(epoch) + ".png") #    :     ,    # (    , , ,  , #    ,     ) #mlab.clf() #mlab.close() #    -      ''' fpoint = ( (np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2 ) for i in range (0, 360, 2): mlab.view(focalpoint=fpoint, distance=25, elevation=75, azimuth=i) mlab.move((0,0,10)) mlab.savefig("act-2d-azimuth" + str(i) + ".png") ''' 

, Mayavi , . , , , .

Mayavi, Matplotlib/axes3d, 3- OpenGL. , ( ) , Qt. mayavi . pip PyQt5 python-qt (, - , 'qt'). , , , , , :

 env QT_API=pyqt python3 gradient-2d.py 

— $$$J(w)$

 def sse_(X1, X2, y, w0, w1, w2): return ((w0+w1*X1+w2*X2 - y)**2).sum() #      J(w0, w1, w2) #   w0, w1  w2 #   eta = 0.001 #      () epochs = 70 w0_first = -.9 w1_first = -.9 w2_first = -.9 #      w0_epochs = [w0_first] w1_epochs = [w1_first] w2_epochs = [w2_first] delta_w0_epochs = [] delta_w1_epochs = [] delta_w2_epochs = [] w0_next = w0_first w1_next = w1_first w2_next = w2_first for i in range(epochs): grad_w0 = (w0_next + w1_next*X1 + w2_next*X2 - y).sum() delta_w0 = -eta*grad_w0 grad_w1 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X1).sum() delta_w1 = -eta*grad_w1 grad_w2 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X2).sum() delta_w2 = -eta*grad_w2 w0_next = w0_next + delta_w0 w1_next = w1_next + delta_w1 w2_next = w2_next + delta_w2 delta_w0_epochs.append(delta_w0) delta_w1_epochs.append(delta_w1) delta_w2_epochs.append(delta_w2) w0_epochs.append(w0_next) w1_epochs.append(w1_next) w2_epochs.append(w2_next) #     sse_epochs = [] for i in range(len(w1_epochs)): sse = sse_(X1, X2, y, w0_epochs[i], w1_epochs[i], w2_epochs[i]) sse_epochs.append(sse) #print('epoch=%d, w0=%f, w1=%f, w2=%f, SSE=%f, SSE/2=%f' % # (i, w0_epochs[i], w1_epochs[i], w2_epochs[i], sse, sse/2)) sse_epochs = np.array(sse_epochs) #  -      η (--) plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, η=%s'%eta) plt.xlabel(u'epoch (η=%s)'%eta) plt.ylabel(u'J(w)') plt.legend(loc='upper right') plt.show() 

12 :

70 :

, , : 6-12- , 70- — 70- , 30-, 40- 200-, , , , .

Conclusión

ADALINE (adaptive linear neuron — ) — . scikit-learn ADALINE ( - , ) , , - « 80-» (ADALINE 60-), .

«Python » ( scikit-learn) , - .

ADALINE .

-, — , : , , , .

-, () , , , ( , , $$$y$) — , scikit-learn.

PS , ADALINE . , , , , ADALINE - , . , ADALINE . , - .