Solo división, o cómo crear una teoría matemática y ganar $ 400K con ella. Serie dos, penúltima

En la serie anterior , examinamos números fraccionarios que no incluían números racionales. Hoy, es precisamente esta parte, no considerada, la que nos espera, y también nos prepararemos para una parte final un poco más complicada sin usar términos como anillos de clases de residuos o módulo de comparación con logaritmo discreto. También en la tercera parte de los interesados, están esperando premios de $ 400K. ¿Por qué en el tercero? Porque sin una introducción al tema, no siempre es fácil entender las razones por las cuales los premios no son tan fáciles de obtener. Y después de leer: solo suerte y alguna actividad decidida, paciente, pero no muy difícil, eso es todo lo que necesita.

Estrellas racionales

Para responder las preguntas anteriores sobre números racionales, nuevamente necesitamos una pequeña digresión. Primero, recuerde que en el proceso de dividir por la "esquina" constantemente obtenemos el resto de dividir una cierta parte del número divisible por el divisor. En este caso, toda la parte de la división se escribe en el resultado, y el resto de la división se multiplica por la base del sistema de números, después de lo cual se repite el procedimiento de división con el resto hasta que se detecta el período o se reducen todos los factores del divisor y obtenemos la fracción final.

Se ve así:

5 | 3 ------ 1.66(6) 3 20 18 20 18 2 ... 

Aquí, el resto de restar 18 de 20 siempre es igual a dos, que luego multiplicamos por la base del sistema de números decimales.

Ahora pensemos en cómo la división de 5 por 3 difiere de, por ejemplo, la división de 1 por 3. La respuesta es simple: la presencia de la parte entera como resultado. Pero nos preguntamos sobre el período y la parte que va antes del período (llamado pre-período), pero no está incluido en la parte completa del resultado. Por lo tanto, no necesitamos considerar toda la parte. Por lo tanto, en este ejemplo, todos los números mayores que 3 o iguales pueden excluirse de la consideración. Y lo que es aún más interesante: las leyes de división se manifiestan en muchos aspectos sin ningún otro número, excepto uno. Es decir, es suficiente estudiar la división de una unidad en una serie de enteros, grandes, y entenderemos cómo responder a todas las preguntas formuladas, y al mismo tiempo nos encontraremos con un número muy decente de nuevas estrellas.

Mientras tanto, no hemos comenzado un estudio serio del tema, algunos trucos. ¿Sabes que compartir se puede hacer "viceversa"? No como estamos acostumbrados desde la escuela, sino comenzando desde el final. Demostremos esto en otro ejemplo, en el que tomamos el último resto y, a partir de él, calculamos el período de fracción. Recuerde que el resto al dividir 5 entre 3 fue igual a 2. ¿Cuál fue el último número que restamos para obtener un deuce? No necesitamos recordar, porque sabemos que siempre restamos los números del resto anterior multiplicado por 10, es decir, el último dígito de la disminución siempre es igual a 0. Esto significa que es suficiente ordenar los productos del triple por números del 1 al 9, = (3,6 , 9,12,15,18,21,24,27), para ver, entre ellos, solo uno termina con 8 y, en total con el resto 2, da cero en el último dígito del decrementado. Entonces, antes de obtener el resto de 2, restamos 18 de 20. ¿Por qué de 20? Porque cualquier otro número con cero en el último dígito dará a la diferencia X0-18 más de tres o menos de cero. De la misma manera, calculamos todos los otros números:

2 - residuo conocido
18 - adición al número con cero, mostrando simultáneamente el valor del siguiente dígito como resultado - 6 (6 * 3 = 18)
20 es un número adecuado con cero
2 - un número con cero antes de multiplicar por 10 (= 20/10)
18 - adición al número con cero
20 es un número adecuado con cero
...

Como resultado, obtenemos exactamente la misma secuencia que cuando se divide por una esquina, pero "por otro lado". Por lo tanto, puede calcular "desde el final" el período de cualquier fracción periódica. Y cuál es el período anterior (y la irrelevancia de su cálculo para este caso en la forma que se muestra) veremos más adelante. La parte completa del resultado siempre es cero cuando se usa la unidad como dividendo, por lo que nuevamente nos vemos privados de la necesidad de calcular otra cosa, excepto el período.

Ahora recuerda cómo dividimos la unidad en tres: $$$1/3 = 0.3 (3)$ . Aquí todo es simple, el período es corto, no hay pre-período, parece no ser nada notable. Pero intentemos multiplicar el resultado de la división nuevamente por tres: $$$0.3 (3) * 3 = 0.9 (9)$ eso es $$$0.9 (9) /3=0.3 (3)$ . Y al principio fue así: $$$1/3 = 0.3 (3)$ . ¿No notas la diferencia? Había uno en la entrada, y después de acciones directas e inversas, obtenemos ... ¿Cómo podría llamarlo más fácil? Es decir, si rastreamos toda la cadena de nueves hasta el infinito, entenderemos que tenemos una unidad, pero aún así no es así, ¿puedes encontrarla? Bueno, no como el original, y eso es todo. Los matemáticos dirán que estas son solo dos formas de notación del mismo número, pero la comprensión cotidiana de los "mismos" se rebela un poco en contra de tales definiciones. En principio, es difícil estar en desacuerdo con los matemáticos, porque muchos nueves después del punto decimal difieren de la unidad por algo completamente efímero, infinitamente pequeño y tienden a cero en el límite. Pero específicamente, ¿puedes abarcar con tu mente todo este conjunto de infinitos? Un número infinito de nueves, una diferencia infinitamente pequeña, que tiende a cero cuando se mueve a lo largo de una serie de nueves al infinito. Y ahora compare esto con tal registro: 1. Una señal, y todo está claro para nosotros. ¿Y cuántos signos hubo en las discusiones sobre la igualdad de un número infinito de nueves a uno? Es decir, ¿todavía hay una diferencia? ¿O su cerebro ignora fácilmente tales pequeñeces en un conjunto de diferencias? Pero si no vamos a la interminable mirada mental en la lista de nueves, entonces, en el lugar donde nos detenemos, inmediatamente habrá una diferencia que incluso los matemáticos reconocerán como significativa: si no ve todos los otros nueve, entonces no somos ninguno. Por lo tanto, surge la pregunta: ¿puedes ver las profundidades de todo el infinito? En general, lo que quieras, los matemáticos han ordenado que este fenómeno se considere el mismo número. Por lo tanto, después de considerar esta estrella (con la franqueza, un brillo extraño), pasamos a la siguiente.

Una conclusión interesante se desprende del hecho de detectar un número infinito de nueves: si el divisor de la unidad es un primo mayor que 3, entonces el período resultante siempre se divide por 9 y, por supuesto, por 3, y también con su longitud de más de un carácter, por 11, y cuando incluso más personajes: 13, 37, 101, etc. Y todo esto es independientemente del divisor de la unidad, si solo fuera simple y más de tres. Puede verificarlo usted mismo, por ejemplo, divida el período 1/7 igual a 142857 por 3, 9, 11, 13, 37.

Bueno, antes de los montones hacemos una pregunta simple: ¿es posible construir el período usted mismo? Si puedes. Por ejemplo, queremos obtener el período 0123456789, ¿podemos encontrar un dividendo y un divisor que den algo similar? Usted puede! Pero sin el número 8. Entonces será 1/81. Y para que el número 8 aparezca en el lugar que le corresponde, necesitaremos agregar al número 81 bastantes dígitos después del punto decimal, o sin un punto decimal, pero luego habrá muchos ceros en el período.

Otra regularidad: para algunos divisores de unidades, no podemos calcular el período en absoluto, sino simplemente cambiarlo cíclicamente cuando multiplicamos el dividendo (unidad) por cualquier número. Por ejemplo: 1/7 = 0. (142857) y 2/7 = 0. (285714), 5/7 = 0. (714285), 3/7 = 0. (428571) y así sucesivamente. Si el dividendo es mayor que 7, entonces toda la parte del resultado de la división irá a la parte anterior al punto decimal, y el período seguirá consistiendo en los mismos seis dígitos, pero nuevamente desplazado cíclicamente: 25/7 = 3. (571428), 86/7 = 12. (285714) etc. Como te gusta eso ¡Cualquier número cuando se divide por 7 da un conjunto de los mismos números! Cualquiera! Absolutamente cualquiera. Y sí, estos "cualquier número" son un número infinito. Y el resultado siempre incluye 6 de los mismos números. Además, comprenderá por qué el mundo de los números está tan estructurado, pero por ahora, notamos que al dividir la unidad por 7, recibimos implícitamente toda la información necesaria para calcular el período a partir del resultado de que cualquier otro número sea siete, porque ahora sabemos que es suficiente solo cambiar cíclicamente uno El único resultado de la división. Es decir, una vez más se confirma que no hay necesidad de lidiar con la división de cualquier número, excepto uno, por el número elegido para el estudio. Es cierto que puede ser necesario multiplicar por algunos números y recordar resultados intermedios, pero más sobre eso más adelante.

Ahora para una vista más general, mostraremos el "mapa de batalla". Se dibuja un mapa para dividir la unidad por el número en estudio, mientras que la división se realiza en todos los sistemas de números con una base menor que el número en estudio. El mapa no incluye el resultado de la división, es decir, el período de la fracción en cuestión, sino que contiene los residuos obtenidos en cada etapa de división por la "esquina". Así es como se ve:


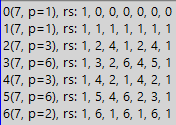
En la tabla anterior puede ver las líneas, de 0 a 6. 0 también es la base del sistema numérico. ¿No estas de acuerdo? Tratemos de convencer. ¿Qué es un sistema numérico? Esta es la base, multiplicada por un cierto valor, y luego agregada al resultado, que al principio es cero. Entonces todos los números se obtienen, por ejemplo, en el sistema de números decimales. ¿Y si la base es cero? Entonces, todos los términos multiplicados por cero también serán iguales a cero. ¿Pero qué cambia eso? ¿Hemos violado la regla de construir números en el sistema numérico elegido? Por lo tanto, para la generalidad de la imagen en el mapa de batalla, utilizamos todos los sistemas de números, del 0 al 6 en el caso de estudiar el número 7. Pero además de la generalidad, la línea con ceros tendrá un propósito adicional.

Pero, ¿qué significan todas estas líneas? Cada fila nos muestra la secuencia de residuos al dividir la unidad por siete en el sistema de números, que está firmado en la columna más a la izquierda. Es decir, al dividir 1/7 en un sistema con una base de 0, tenemos un resto inicial de 1 (la unidad que dividimos). Además, como siempre hacíamos al dividir por una esquina, multiplicamos el primer resto por la base del sistema numérico. Tenemos cero. Ahora cero es el resto actual. Por lo general, al calcular el cociente después de recibir el resto igual a cero, y si no hay dígitos adicionales en el número divisible, la división se detiene (ya que se obtiene el resultado). Pero en nuestro caso, completamos una tabla que no tolera el vacío, y además de la impaciencia, tiene propiedades adicionales que también requieren la presencia de cualquier número en todas las celdas. Por lo tanto, continuamos dividiendo y dividiendo el resto de 0 entre 7. Por lo general, mientras que el resto es más pequeño que el divisor, se multiplica por la base del sistema numérico, pero multiplicar por cero muchas veces es inútil, por lo que simplemente escribimos que después de multiplicar por cero el resto vuelve a ser cero nuevamente, y Ahora póngalo en la tabla en la celda siguiente. Luego repita el procedimiento. Y así llenamos todas las celdas en la primera fila con ceros. Y luego complete la segunda línea. Pero ya tiene otra base del sistema de números: una unidad. Después de dividir 1 entre 7, tenemos el primer resto, uno. Luego multiplicamos por la base del sistema numérico, es decir, por uno. Obtenemos nuevamente 1. Escribimos en la celda apropiada. Nuevamente multiplicamos por 1, nuevamente obtenemos 1, escribimos nuevamente. Y así sucesivamente hasta que se complete la segunda línea. Pero después de estas dos líneas maravillosas en todos los aspectos, finalmente llegamos a una división más significativa: en el sistema binario (y el significado de los dos primeros sistemas se aclarará más adelante). Primero tenemos la misma unidad. Escribe la unidad en la tercera línea. Luego multiplicamos por la base del sistema numérico (por 2). Obtenemos 2. 2 menos que siete, todavía no podemos restar, así que escribimos el resto 2 en la tabla. Nuevamente, multiplicamos por 2, obtenemos 4, que nuevamente es menor que 7, así que nuevamente va a la tabla sin cambios. Pero en el siguiente paso obtenemos 8, que es más de 7, por lo que debemos restar. El resultado es 1. Escribimos en la tabla. Pero antes ya teníamos una unidad, por lo que todos los demás pasos serán los mismos, por lo que agregaremos la tercera línea al final. Y de la misma manera agregaremos el resto de las líneas, pero sin olvidar que necesitamos multiplicar por otra base del sistema numérico.

Entonces, cuando finalmente obtuvimos la tabla completa, podemos sacar algunas conclusiones. Primero, preste atención a las repeticiones. Para el sistema binario, tenemos 1,2,4,1,2,4,1, es decir, dos veces 1,2,4 y luego una vez más 1. Aquí, la lista 1,2,4 corresponde al período de la fracción binaria resultante. Es decir, el período será de duración 3. Y aunque utilizamos los restos en lugar de los números del período, la duración no sufrió esto y, por lo tanto, toda la información se guarda. Y aún más: en la tabla hay realmente más sobras de información. Pero más sobre eso más adelante, pero por ahora, notamos que todas las líneas están hechas de la misma longitud para facilitar el estudio y debido a la presencia de tantas propiedades útiles. Entonces, las líneas comienzan y terminan con unidades, que distinguen bien las propiedades del número 7. Y si redujimos las líneas a la longitud del período, no podríamos disfrutar de la belleza de la visualización simétrica de la esencia del número 7.

Ahora sobre la información. Los saldos establecen inequívocamente el número en la posición correspondiente del período, por lo tanto, la información en esta representación no se pierde, pero dado que los saldos pueden ser mayores, por ejemplo, el máximo de una posición decimal (es decir, 9), la información con su participación se convierte en la más completa, porque una posición en el sistema El cálculo no puede decirnos que el resto fue, por ejemplo, 19, pero el resto 19 dirá claramente qué figura está en el período y de qué resto anterior restamos el producto del dividendo (recuerde el enfoque con la división "desde el final"). Y además, notamos de inmediato una cosa simple: no puede haber más residuos que $$$N-1$ donde $$$N$ - el número investigado por el cual dividimos la unidad. Este es un punto muy importante. Además, se puede demostrar fácilmente que si un residuo encontrado previamente se repite al dividirlo por una esquina, entonces se repetirá la secuencia completa de residuos que siguió al valor repetido anteriormente. Por lo tanto, no necesitamos tomarlo más, una vez que se encuentra el período. Si registramos solo los números del período, entonces repetir los números en el período no significa la finalización del cálculo. Por lo tanto, los saldos son más importantes que las cifras del período. Pero lo más interesante son los restos de todo. $$$N-1$ y, por lo tanto, los períodos son más largos $$$N-1$ no puede ser Entonces, aquí acabamos de encontrar el límite superior del número de dígitos en el período, pasando de los dígitos reales del período a los saldos. Como dicen, fácil movimiento de la mano y sin fraude. Este es el beneficio de una información más completa. Bueno, por lo tanto, el ancho de nuestro "mapa de batalla" para 7 partidos es de 6 + 1 columnas, es decir, 6 columnas para todos los residuos posibles y 1 columna para detectar la simetría de las unidades, que de ninguna manera es obligatoria para todos los números, y por lo tanto no es Vale la pena esconderse, ahorrando espacio debajo de una columna.

Bueno, ahora eche un vistazo al "mapa" anterior en términos de su utilidad. Puede notar de inmediato un conjunto de patrones simples. Cada línea comienza con una unidad y termina con ella. La segunda posición de cada línea indica la base del sistema de números, pero el centro de cada línea contiene N-1 o 1. Tenga en cuenta que no hicimos ningún esfuerzo para organizar los números en la tabla en el orden indicado, excepto por simplemente arreglar los resultados de la división en la tabla. Pero a pesar de que ignoramos cualquier orden (excepto la secuencia de pasos de división), el orden en sí surgió de la nada y nos sacó la letra P de las unidades, le puso una gorra de ceros (con una visera de uno), dividió la tabla por una columna central de unidades, y sus adiciones al número 7 (según la fórmula 7-1 = 6). Además, la orden misma colocó los sistemas numéricos en la segunda columna. Compárelo con los números en la primera columna de la izquierda, solo se agregan intencionalmente, para que sepamos exactamente dónde está el sistema de números. Bueno, nosotros mismos podemos calcular fácilmente el período de las fracciones resultantes, aunque por conveniencia se indica en la columna con valores de la forma p = X.

De hecho, ante ti hay algo así como una tabla periódica, pero no para la química, sino para la teoría de números. De la misma manera que Mendeleev, solo puede mirar la tabla para encontrar un cierto patrón, y luego, al igual que después de Mendeleev, la existencia de este patrón puede justificarse y demostrar que se repite para todos los números que satisfacen un cierto conjunto de condiciones. Y esto es lo más importante en tales tablas. Simplemente observando y observando patrones, puede descubrir leyes, por ejemplo, la teoría de números. Bueno, para los lectores más reflexivos, el camino hacia un ciclo completo se abre aquí: después de encontrar un patrón, debe probar (o refutar) su relevancia para todos los números o para los números de una clase determinada.

Como se señaló, esta tabla contiene información completa sobre el número primo 7. Pero de esta información podemos derivar hipótesis con respecto a todos los números primos. E incluso algunas de estas hipótesis ya se nos han demostrado, por lo que solo tenemos que verificar las conclusiones de los demás. La evidencia fue dada por personas tan famosas como, por ejemplo, Fermat y Euler. Farm nos dio esta fórmula $$$a ^ {(p-1)} \ pmod p = 1$ (aquí la operación de modificación toma el resto de dividir el valor de la izquierda por el valor de la derecha, en la programación generalmente se indica con el símbolo%), es decir, el resto de la división $$$a ^ {(p-1)}$ en p siempre es igual a uno para todos los primos (es decir, primos, esto es importante). Pero el número 7 también es primo. Y cada residuo en cada fila se puede calcular usando la siguiente fórmula: $$$b ^ i \ pmod N = r$ . Aquí b es la base del sistema numérico (de la base inglesa), i es el número de posición en la línea (del índice inglés), comenzando desde cero para la primera posición, N es el número bajo investigación (en este caso - 7), r es el resto (del recordatorio inglés) ) formado en el paso i-ésimo de dividir por una esquina y contenido en la columna i-ésima de la tabla. Comparemos la fórmula de Fermat y la fórmula para calcular el resto especificado por el índice i. Son idénticos para el último miembro de todas las secuencias de residuos. Y de acuerdo con la fórmula de Fermat, para cada resto en posición $$$N-1$ Tenemos igualdad para la unidad. Es decir, el patrón observado a simple vista en forma de una columna de unidades fue confirmado y probado en el tiempo de Fermat (aunque Fermat no nos dio pruebas, pero por lo general todas sus afirmaciones eran ciertas). Euler agregó a la fórmula de Fermat la capacidad de usarla no solo para números primos, sino también para números compuestos. Es cierto que necesita conocer todos los divisores de un número, pero para números pequeños esto no es un problema. Entonces, en la segunda tabla (a continuación) vemos la secuencia de residuos para el número 21, que es compuesto. Euler demostró que el resto de dividir un número arbitrario en el grado igual al número de números más pequeños y no tener divisores comunes con N también es igual a uno. Y es precisamente este hecho el que observamos en la tabla para el número 21, para cuál de los 20 números más bajos, 8 tienen un divisor común con 21 y 12 no. Por lo tanto, observamos en la columna 12 (al indexar desde cero) muchas unidades. Y estas unidades no están al final de las líneas, porque algunos de los números que son menores que 21 tienen divisores comunes con 21.Pero para los números primos, ningún número más pequeño tiene divisores comunes con ellos, por lo que el número de números sin divisores comunes en simple siempre es mayor que en compuesto. Y por lo tanto, los residuos unitarios en la tabla para los simples son más lejanos que para los compuestos. Pero tenga en cuenta que no todos los valores en la columna 12 de la tabla para 21 son iguales a uno. ¿Euler está equivocado? No, simplemente no tenía la intención de usar su fórmula para trabajar con números que se pueden reducir, y solo en las líneas que son múltiplos de 3 y 7 (divisores de 21) tenemos una discrepancia con la fórmula de Euler. En general, resulta que Fermat y Euler nos dieron fórmulas adecuadas útiles para comprender los problemas de divisibilidad de los números, y las tablas anteriores en todo su esplendor confirman los resultados de Euler y Fermat.


Aunque vale la pena señalar que ni Fermat ni Euler sabían sobre la tabla anterior. Y si lo sabían, entonces nadie se enteró de ella. Aunque, por otro lado, en sus días, las anotaciones decimales alternativas eran algo menos populares que en nuestro tiempo. Entonces, incluso no todos sabían sobre el sistema decimal, pero solo contaban con los dedos. Y por lo tanto, el Fermat deducido, y luego la fórmula extendida por Euler para vincular la base y el grado, no nos dan una explicación de las otras leyes de esta tabla. Por lo tanto, nos esperan más estrellas, y luego el período de apertura condicional de las capas electrónicas de los átomos, con la ayuda de los cuales los químicos finalmente explicaron las propiedades predictivas mágicas de la tabla periódica. Pero comencemos con la magia.

De las estrellas a la magia.

Los amantes de los rompecabezas conocen los llamados "cuadrados mágicos". Estas son tablas en las que necesita organizar los números de tal manera que las sumas a lo largo de las verticales, horizontales y dos diagonales sean iguales. Muchas personas extrañaron una y otra vez durante mucho tiempo poniendo números en el lecho Procrustean de restricciones sobre las cantidades, e incluso lograron llenar cuadrados bastante grandes. Pero hoy nos encontramos con una magia mucho más poderosa. Sí, la tabla periódica para la teoría de números contiene muchas más restricciones, e incluso un estudiante de primer grado que puede aprender a compartir la "esquina" puede llenarla. Piénselo: las personas más inteligentes llenaron los cuadrados mágicos, pero no encontraron un método común de relleno, o incluso avanzaron en tamaño a un miserable centenar de columnas. Y el niño de primer grado hará frente por completo incluso a mil millones, si solo tuviera suficiente tiempo disponible.Aquí hay una galaxia así, llena de estrellas hasta los globos oculares, esperándonos en cuadrados numéricos.

Comencemos enumerando los patrones obvios

Multiplicación Cualquier fila de la tabla se puede multiplicar por cualquier otra. El resultado será una serie cuyo número se calcula como el producto de los números de la serie multiplicada dividido por el resto por el número en estudio. Es decir, si multiplicamos la fila 2 de la tabla por 7 por la fila 3, entonces obtenemos la fila 6. Y si multiplicamos la fila 4 por la fila 6, obtenemos 24 mod 7 = 3, es decir, la tercera fila. Y la propiedad misma del módulo de división (es decir, con el resto) hace que todos los sistemas numéricos, más grandes que el número en estudio, sean innecesarios. Por lo tanto, no necesitamos un sistema de números con base 24, porque los valores de los residuos en él serán exactamente los mismos que en el sistema con base 3. En cualquier sistema de números que calculemos los restos de 1/7 de división, siempre obtenemos un resultado que ya es esta en la mesa. Interesante? Y esto es solo el comienzo.

Simetría Cada segunda columna contiene las partes superior e inferior, que son un reflejo de la otra. Y las columnas restantes contienen valores iguales al complemento del balance N reflejado. Es decir, en la segunda columna de la tabla para el número 7, el número 1 complementa 6 a 7, 2 suplementos 5 y 3 suplementos 4. Como resultado, la fórmula considerada anteriormente$$b i( modN ) = r se complementa con el siguiente sistema:$b^i \pmod N = r$

$$( N - j ) i( modN ) = r , para columnas impares$(N-j)^i \pmod N = r$
$$j i( modN ) = r , para columnas pares$j^i \pmod N = r$
$$j = N - b Aquí N es el número en estudio (por ejemplo 7), b es la base del sistema de números, i es el índice de la columna a partir de cero, r es el valor restante en la celda dada de b e i.$j=N-b$



La simetría horizontal se expresa mediante las columnas extremas de unidades mencionadas anteriormente y la columna central de unidades y su complemento a N. Esto funciona exactamente para los números primos, pero para los componentes hay desviaciones. Además (de nuevo solo para los números primos, pero a veces también para los componentes), la columna intermedia que se divide siempre comienza con una unidad del período de repetición de los residuos o da a la derecha una serie de adiciones a N para la mitad izquierda de la serie. Es decir, si la unidad está en la columna central, la parte izquierda se repite. Si hay una adición a N, entonces continúa el mismo lado izquierdo, pero después de restar de N. Por lo tanto, de toda la tabla (para números primos) puede dejar solo el cuadrado superior izquierdo con el lado$$( N - 1 ) / 2 (sin una fila cero), y todos los demás valores residuales se derivan inequívocamente en función de la información de dicho cuadrado. Aunque no debe olvidar que, en general, toda la tabla se deriva del conocimiento de un solo número: el divisor, mientras que el dividendo es una constante igual a 1.Ahora la suma. Básicamente para simple, pero a veces para compuesto, se siguen las reglas que se muestran a continuación. La suma horizontal (sin la última columna agregada para mayor claridad) es siempre un múltiplo del número bajo investigación. La suma vertical también es siempre un múltiplo del número bajo investigación. Las sumas de los saldos dentro del período de uno a uno (el período puede ser menor que el ancho de la tabla) son múltiples o iguales al número bajo investigación.$(N-1)/2$



Mayor divisibilidad. Las filas de residuos entre unidades (períodos de residuos) pueden ser de diferentes longitudes, pero todas las longitudes de las filas para números primos siempre dividen la longitud total de la tabla por un número entero. Es decir, si al menos una fila entre unidades no divide completamente la longitud total de la tabla, entonces este es un número compuesto (compare las tablas para 21 y 7).

Longitud y singularidad. Cada fila de longitud uniforme y más corta que el ancho de la tabla consta de dos partes: una serie de residuos en el medio, y después una serie de adiciones a N para la serie inicial de residuos. Además, todos los valores dentro del período son únicos, es decir, se repiten solo con la repetición del período, pero dentro del período nunca se repiten.

Multiplicación Si cada celda de la tabla se multiplica por un número entero, obtenemos un desplazamiento cíclico de residuos en el caso de una longitud de período igual al ancho de la tabla, o una nueva serie en los casos en que el período es más corto que el ancho de la tabla. Además, en el caso de períodos cortos, todos los valores en la nueva serie serán únicos, es decir, ninguno de ellos está en la serie obtenida dividiendo la unidad por el número en estudio, así como en la serie obtenida multiplicando por otros números y en la serie original, que multiplicado por una constante. En total, el número de períodos únicos es igual al ancho de la tabla dividido por la duración del período (para números primos). Y para los componentes en todos los períodos posibles no hay residuos "prohibidos", que, cuando se multiplican por filas que son divisibles por los divisores del número en estudio, dan un resto de cero, pero más sobre eso más adelante.

Como resultado de la multiplicación en serie, se puede obtener un cambio de período cíclico o un nuevo período. El nuevo período también se puede desplazar cíclicamente, multiplicándolo por otros valores. La regla general para elegir un turno o un nuevo período es simple: si en el período restante hay un número por el cual multiplicamos, obtendremos un cambio cíclico, y si no existe ese número, obtendremos una nueva serie. Y, por supuesto, esto se aplica directamente a las fracciones periódicas, más precisamente a sus períodos (es necesario distinguir los períodos de los saldos de los períodos de los números en el registro de fracciones, aunque generalmente la diferencia es clara desde el contexto). Entonces, en el ejemplo del número 7 que se mostró anteriormente, vimos que no importa cómo multiplique el resultado de dividir por 7, siempre obtenemos el mismo conjunto de dígitos en el período, pero cambiamos cíclicamente en relación con la división estándar 1/7. En el caso del número 7, tenemos un punto (en notación decimal) con una longitud,coincidiendo con el ancho de la tabla, por lo tanto, no se pueden obtener otros números en ella (no hay más saldos disponibles), pero solo son posibles los cambios cíclicos. Pero hay un punto más: compartimos en el sistema decimal, pero no existe esa línea en la tabla. Esto significa que para encontrarlo necesitamos dividir 10 entre 7 y obtener el resto - 3. Es el sistema de números con base 3 que repite completamente el comportamiento del sistema decimal con respecto a los restos, por lo tanto, es en la tercera fila donde vemos el período completo, es decir, con una longitud igual a El ancho de la mesa. Y para obtener el período en términos decimales de los saldos, puede tomar cualquier resto y comenzar a dividirlo por la esquina, luego como resultado habrá todos los dígitos del período de la fracción. El cambio del período durante la multiplicación se determina al encontrar el resto de la división del factor por N en la serie de residuos. El cambio será igual al índice del saldo encontrado,es decir, siempre necesitamos cambiar cíclicamente el período de derecha a izquierda por el número de dígitos igual al índice del resto encontrado.

Y algunas dependencias entre los diversos números estudiados:


Aquí vemos filas para números del 2 al 39 en el sistema binario. Presta atención a la fila inferior. De ella suben columnas de números 1,2,4,8,16,32. Después del número 32, vemos una columna de valores que aumenta en uno (25,26,27, ...). En la siguiente columna, los valores aumentan en tres. Luego el 6, 13, 26, etc. El aumento "cambia" después de alcanzar un valor que es mayor que el número bajo investigación (la columna a la izquierda entre paréntesis, antes de la duración del período). Entonces, el crecimiento por uno cambia al crecimiento por dos, luego por tres, etc. En general, todas esas columnas comienzan con$$2 i , donde i es el índice de la columna. Abajo$2^i$$$2 i el valor no cambia, pero arriba cambia de acuerdo con la fórmula$2^i$$$2 i / j , donde j es el incremento al desplazar una fila hacia arriba (mayor que cero). Es decir, mientras el número de fila está entre$2^i/j$$$$2^i/j$ y $$2 i / ( j + 1 ) , el incremento es igual a j. Después de cruzar la frontera$2^i/(j+1)$$$2 i / ( j + 1 ) , el incremento se vuelve igual$2^i/(j+1)$$$j + 1 , entonces el borde será$j+1$$$2 i / ( j + 2 ) , luego el incremento será$2^i/(j+2)$$$$j+2$ etc. , 10 ( ), , , 2 .

, , , , 11, 13, 17. , . - , !

Los propietarios de bolas de cristal tienden a predecir el futuro, pero también podemos predecir algo de nuestras tablas. Probablemente ya lo haya notado: las últimas columnas pares de unidades se encuentran solo en números primos. Es decir, un vistazo a la tabla es suficiente para comprender si un número es un número primo o no. Esta es la primera predicción para nuestra bola de cristal. La segunda predicción es el período de fracción en el sistema numérico.$$k ∗ N - 1 (aquí k es cualquier número entero mayor que cero) siempre es 2. El período de fracción en el sistema numérico$k*N-1$$$k ∗ N + 1 es siempre igual a 1 y todos los valores también son iguales a 1. Por ejemplo, para el número estudiado N = 11 con k = 1, tenemos$k*N+1$$$k ∗ N - 1 = 10 , es decir, en el sistema de números decimales$k*N-1=10$$$1 / 11 = 0. ( 09 ) , la longitud del periodo es igual a 2, como se predijo anteriormente. Ahora predecimos el complemento de las fórmulas de Euler y Fermat. Primero, recuerde que cada resto puede calcularse teniendo su número de posición y la base del sistema numérico usando la fórmula$1/11=0.(09)$

$$b i( modN ) , donde b es la base del sistema de números, i es la posición a partir de cero, N es el número bajo investigación. Esta fórmula corresponde a las fórmulas de Fermat y Euler, si en ella tomamos la posición igual a los valores propuestos por Fermat y Euler. Pero además del patrón$b^i \pmod N$$$a ( p - 1 )( modp ) = 1 que nos dio Fermat, la regularidad de la columna central nos da una fórmula similar:$a^{(p-1)} \pmod p = 1$$$a ( p - 1 ) / 2( modp ) = { 1 , p - 1 } , es decir, cualquier número a la potencia de un primo, menos uno dividido por 2, nos dará la unidad o p-1, donde p es un primo. La fórmula se puede extender al caso cuando el número de períodos de uno a uno dentro de toda la tabla es impar y la duración del período es par.$a^{(p-1)/2} \pmod p = \{1,p-1\}$ Entonces $$una k( modp ) = p - ( a ( p - 1 ) / 2 + k( modp ) ) , donde k es cualquier número entero, p es primo. Esta fórmula refleja la regularidad de la repetición de la segunda parte del período de duración par, pero con la resta del número estudiado, esta dependencia se describió un poco más alto. Para un número par de períodos de longitud par, también se puede expresar mediante la fórmula la dependencia de los residuos de la mitad derecha del período de los residuos de la mitad izquierda. Ahora predeciremos cómo encontrar todos los divisores de un número de dicha tabla. Para hacer esto, mire nuevamente en la tabla el número 21:$a^k \pmod p = p - (a^{(p-1)/2+k} \pmod p)$




Está claro de inmediato que muy pocas filas terminan con una unidad, esto indica la naturaleza compuesta del número. Como Euler mostró en su fórmula para comparar el grado de un número compuesto con el resto de 1, el exponente en este caso no puede ser igual al número compuesto menos uno (es decir, el valor que determina la posición extrema derecha en la tabla), por lo que en el caso del número 21 vemos la mayoría filas sin una unidad al final. Sin embargo, también vemos varias filas con unidades. ¿Por qué la fórmula de Euler no se cumple para ellos? Preste atención a su período, es igual a 2 o 1. Es decir, como es típico para muchas fórmulas, la fórmula de Euler nos da una solución del conjunto, y en este conjunto hay unidades garantizadas en exactamente las posiciones indicadas por la fórmula, es decir, antes del último lugar en la tabla, pero como el período es corto, entonces él,repitiendo muchas veces, a veces cabe con éxito en el ancho total de la tabla y obtenemos uno al final de algunas filas. Esta situación es típica para un conjunto completo de números, que se denominan pseudo-simples, porque suplantan a los simples, colocando unidades en la fila derecha en algunas filas. Pero esto no nos impide ver aquellas series en las que no hay una unidad al final y, por lo tanto, esta situación no afecta de ninguna manera la posibilidad fundamental de determinar la simplicidad o la naturaleza compuesta del número de acuerdo con la tabla propuesta. Aunque en realidad, los principios a menudo se encuentran con limitaciones de nuestras capacidades, pero más sobre eso más adelante.poniendo unidades a la derecha en algunas filas. Pero esto no nos impide ver aquellas series en las que no hay una unidad al final y, por lo tanto, esta situación no afecta de ninguna manera la posibilidad fundamental de determinar la simplicidad o la naturaleza compuesta del número de la tabla propuesta. Aunque en realidad, los principios a menudo se encuentran con limitaciones de nuestras capacidades, pero más sobre eso más adelante.poniendo unidades a la derecha en algunas filas. Pero esto no nos impide ver aquellas series en las que no hay una unidad al final y, por lo tanto, esta situación no afecta de ninguna manera la posibilidad fundamental de determinar la simplicidad o la naturaleza compuesta del número de acuerdo con la tabla propuesta. Aunque en realidad, los principios a menudo se encuentran con limitaciones de nuestras capacidades, pero más sobre eso más adelante.

Ahora los divisores del número 21. Sus períodos comienzan y terminan no por unidades, sino por los propios divisores. Lo mismo se aplica a todas las filas en posiciones que son múltiplos de divisores. Entonces, para el divisor 3, vemos que en la línea No. 3 el período comienza con un triple y termina con él. Lo mismo para la fila número 7 (a pesar de que la duración del período allí es igual a uno). Y de la misma manera, todos los múltiplos de los números de tres y siete filas se comportan de la misma manera. Es decir, la ausencia de una unidad en períodos es un signo de detectar el divisor del número en estudio, o un valor que es un múltiplo del divisor. Bueno, la unidad al comienzo de tales series nos informa sobre la duración del período anterior. Para un número compuesto, el preperíodo existe solo en sistemas numéricos que son múltiplos de los divisores del número. Entonces, si encuentra una fracción con un período anterior, debe saber que se obtuvo después de dividir el número compuesto.La longitud del preperíodo es igual al número de residuos al comienzo de la serie no incluidos en el período de residuos. Al dividir la unidad por el número estudiado, el preperíodo siempre consistirá en ceros. Si multiplicamos el resultado de dividir por otro número (o, de manera equivalente, dividimos el factor por N), entonces obtenemos el mismo período, cuyas reglas para la descripción se dan arriba, más la parte del resultado de multiplicar el factor por los bits más antiguos en el período anterior. Si el número multiplicado es mayor que N, parte de los bits más significativos irán a la parte entera del resultado, y el período anterior seguirá siendo la misma longitud.Las reglas para la descripción de las cuales se dan arriba, más la parte del resultado de multiplicar el factor por un período que desapareció por los dígitos más altos en el período anterior. Si el número multiplicado es mayor que N, parte de los bits más significativos irán a la parte entera del resultado, y el período anterior seguirá siendo la misma longitud.Las reglas para la descripción de las cuales se dan arriba, más la parte del resultado de multiplicar el factor por un período que desapareció por los dígitos más altos en el período anterior. Si el número multiplicado es mayor que N, parte de los bits más significativos irán a la parte entera del resultado, y el período anterior seguirá siendo la misma longitud.

Tenga en cuenta que si multiplicamos la tabla completa para un número compuesto por un múltiplo de cualquier divisor del número en estudio, obtenemos la degeneración de la tabla cuando se convierte casi en una copia de la tabla de otro número obtenido después de reducir el investigado por su divisor. Entonces, debajo hay una tabla para el número 21 veces 3, y debajo hay una tabla para el número 7 veces 3. Si las comparas, resulta obvio que tenemos casi una copia de la tabla para el siete, pero son tres veces más anchas y altura Una copia completa no funcionará, porque en la tabla para 21 números que son mayores que 7 son válidos, y en la tabla para 7, dichos números no son válidos. Pero si tomamos esto en cuenta y dividimos con el resto de los valores en la tabla para 21 por el número 7, entonces las tablas convergerán. Aunque el ejemplo de esta copia casi puede asegurar que fuera de la subtabla para 7, dentro de la tabla para 21,son, como se mencionó anteriormente, copias completas, que tiene sentido simplemente eliminar para facilitar la percepción.



Además, preste atención a las filas de ceros con las líneas No. 7 y No. 14. Nos dicen claramente sobre la divisibilidad del número 21, porque multiplicamos el resultado de dividir 1/21 por 3, que se reduce y da el resultado 1/7, pero la fila número 7 en este caso muestra el resultado de dividir 7/7, donde todos los restantes son 0. La fila número 14 es el resultado de la división 14/7, y allí el resto es igual a cero.

, 3 №7 14 , 7, , , , 21. , , , , , 3, №7 14, . , . 21 3 7, , 3 7 . , 3, , 3. , №7 14, , , . , 3 7 14. . 7 14? — 3 , 3. , . , , ( ) . . ? .

¿Por qué puedo usar las tablas descritas? Por ejemplo, nos dan la oportunidad de generar secuencias pseudoaleatorias. Y estas secuencias tienen una serie de propiedades útiles. Entonces, en cada secuencia de residuos no hay repeticiones. Si necesitamos repeticiones (para una imitación más completa de aleatoriedad), entonces tenemos a nuestra disposición valores del período de fracción, que a menudo se pueden repetir. La distribución de residuos del conjunto completo de secuencias para primos es siempre perfectamente uniforme. Los valores de varios residuos se mantienen automáticamente en el rango [1, N-1]. Para obtener secuencias, tenemos un número infinito de primos, lo que hace que el número de secuencias sea ilimitado. La longitud máxima de la secuencia no excede el valor de un número primo, lo que proporciona una manera simple de predecir este parámetro importante.La presencia de varias secuencias, con un período más corto que N, nos garantiza que no hay intersecciones de secuencias cuando se generan en paralelo, es decir, al cargar todos los núcleos del procesador, no tenemos que pensar en bloqueos, sincronizaciones, verificaciones de entrada y similares, lo que aumenta en gran medida la velocidad de la generación en paralelo. Además, el algoritmo de generación (división por esquina) está disponible para estudiantes de primaria, y también es extremadamente fácil de implementar mediante programación.Además, el algoritmo de generación (división por esquina) está disponible para estudiantes de primaria, y también es extremadamente fácil de implementar mediante programación.Además, el algoritmo de generación (división por esquina) está disponible para estudiantes de primaria, y también es extremadamente fácil de implementar mediante programación.

También puedes pensar en el cifrado. Puede predecir la secuencia de residuos conociendo el divisor de la unidad, el sistema numérico seleccionado y cualquier valor de la serie que cifra los datos (después de todo, puede cifrar omitiendo algunos residuos). Incluso cuando algunos métodos revelan algunos valores de la secuencia de cifrado, el criptoanalista aún tendrá que adivinar el número elegido y la base del sistema de números. Si selecciona dos parámetros de órdenes simples de una docena o dos mil millones (y para ellos, debido al tamaño modesto, es muy simple construir una tabla de sus períodos, lo que le permitirá cambiar instantáneamente el cifrado al menos cada segundo), luego, utilizando la fuerza bruta, tal cifrado solo puede descifrarse al no ordenar menos de 10 ^ 18 pares. Pero incluso si rompen un conjunto de datos,luego, después de un cierto intervalo (por ejemplo, cada mensaje tiene su propio par), el par de cifrado cambiará y todo debe comenzar de nuevo, lo que puede no funcionar debido a la incapacidad de obtener el valor de la secuencia de cifrado para cada mensaje (o incluso parte del mensaje, al cambiar la clave después de cuántos byte) Para una computadora normal, esta es una tarea irresoluble. Aunque aquí todo se basa en el descubrimiento de la teoría de la divisibilidad suficiente para tales fines (como en el caso del cifrado asimétrico generalizado).Aunque aquí todo se basa en el descubrimiento de la teoría de la divisibilidad suficiente para tales fines (como en el caso del cifrado asimétrico generalizado).Aunque aquí todo se basa en el descubrimiento de la teoría de la divisibilidad suficiente para tales fines (como en el caso del cifrado asimétrico generalizado).

En la próxima serie, hablaremos sobre la teoría de la divisibilidad y sobre los premios que esperan a los lectores interesados.