Análisis de entrevistas de trabajo de Google: búsqueda de relaciones

Bienvenido al siguiente artículo de una serie de acertijos que pregunté en las entrevistas de Google antes de que fueran prohibidos después de la filtración. Desde entonces, dejé de trabajar como ingeniero de software en Google y pasé al puesto de gerente de desarrollo en Reddit, pero todavía tengo algunos temas geniales. Hasta la fecha, hemos examinado la programación dinámica , elevando las matrices al poder y la sinonimia de las consultas . Esta vez una pregunta completamente nueva.

Pero primero, dos puntos. En primer lugar, el trabajo en Reddit fue increíble. Durante los últimos ocho meses, he creado y dirigido el nuevo equipo de Relevancia de anuncios y he establecido una nueva oficina de desarrollo en Nueva York. No importa cuán divertido pueda ser, desafortunadamente, descubrí que hasta hace poco no me quedaba tiempo ni energía para un blog. Me temo que abandoné un poco esta serie. Perdón por el retraso.

En segundo lugar, si siguió los artículos, después del último número, podría pensar que comenzaría a investigar las opciones sinónimas de las consultas. Aunque me gustaría volver a esto en algún momento, debo admitir que perdí el debido interés en este problema debido a un cambio de trabajo y hasta ahora decidí posponerlo. Sin embargo, ¡mantente en contacto! Me lo debo y tengo la intención de devolverlo. Solo, ya sabes, un poco más tarde ...

Descargo de responsabilidad rápido: aunque entrevistar a los candidatos es una de mis tareas profesionales, este blog presenta mis observaciones personales, historias personales y opiniones personales. No tome esto para ninguna declaración oficial de Google, Alphabet, Reddit o cualquier otra persona u organización.

Busca una nueva pregunta

En un artículo anterior, describí una de mis preguntas favoritas que usé durante mucho tiempo, antes de la inevitable filtración. Las preguntas anteriores eran fascinantes desde un punto de vista teórico, pero quería elegir un problema un poco más relevante para Google como empresa. Cuando se prohibió esta pregunta, quería encontrar un reemplazo, teniendo en cuenta la nueva restricción: simplificar la pregunta.

Ahora, esto puede parecer un poco sorprendente dado el infame proceso de entrevistas en Google. Pero en ese momento un problema más simple tenía sentido. Mi razonamiento consistió en dos partes. El primero es pragmático: los candidatos generalmente no respondían muy bien a las preguntas anteriores, a pesar de numerosas sugerencias y simplificaciones, y no siempre estaba completamente seguro de por qué. El segundo teórico: el proceso de la entrevista debe dividir a los candidatos en las categorías "vale la pena contratar" y "no vale la pena contratar", y tenía curiosidad por saber si esto podría hacerse un poco más fácil con la pregunta.

Antes de aclarar estos dos puntos, quiero señalar lo que no significan. "No siempre estoy seguro de por qué una persona tiene problemas" no significa la inutilidad de las preguntas y que quería simplificar la entrevista por este motivo. Incluso la pregunta más difícil, muchos se las arreglaron bien. Quiero decir, cuando los candidatos tenían problemas, me costaba entender lo que se estaban perdiendo.

Las buenas entrevistas dan una idea general de las fortalezas y debilidades del candidato. No es suficiente que el comité de contratación simplemente diga que "falló": el comité determina si el candidato tiene las cualidades específicas de la empresa que está buscando. Del mismo modo, las palabras "él es genial" no ayudan al comité a decidir sobre un candidato que sea fuerte en algunas áreas, pero dudoso en otras. He descubierto que los problemas más complejos a menudo separan a los candidatos en estas dos categorías. Desde este punto de vista, "No siempre estoy seguro de por qué una persona tiene problemas" significa "la incapacidad para avanzar en este tema no representa en sí una imagen de las habilidades de este candidato".

La clasificación de los candidatos como "vale la pena contratar" y "no vale la pena contratar" no significa que el proceso de entrevista deba separar a los candidatos estúpidos de los inteligentes. No puedo recordar a un solo candidato que no fuera inteligente, talentoso y motivado. Muchos venían de excelentes universidades, y el resto estaba claramente extremadamente motivado. Pasar por entrevistas telefónicas ya es un buen tamiz, e incluso negarse en esta etapa no es una señal de falta de capacidad.

Sin embargo, puedo recordar a muchos que no estaban lo suficientemente preparados para la entrevista o trabajaron muy lentamente, o requirieron demasiada supervisión para resolver el problema, o se comunicaron de una manera poco clara, o no pudieron traducir sus ideas al código, o ocuparon una posición que simplemente no conduciría su éxito a largo plazo, etc. La definición de "vale la pena contratar" es vaga y varía según la empresa, y el proceso de entrevista es determinar si cada candidato cumple con los requisitos de una empresa en particular.

Leí muchos comentarios de reddit quejándose de preguntas de entrevistas demasiado complejas. Tenía curiosidad si todavía era posible hacer una recomendación digna / indigna para una tarea más simple. Sospeché que esto daría una señal útil sin gritar innecesariamente los nervios del candidato. Te contaré mis conclusiones al final del artículo ...

Con estos pensamientos, estaba buscando una nueva pregunta. En un mundo ideal, esta es una pregunta lo suficientemente simple como para resolverla en 45 minutos, pero con preguntas adicionales para que los candidatos más poderosos muestren sus habilidades. También debe ser compacto en la implementación, porque muchos candidatos todavía escriben en la pizarra. Una gran ventaja si el tema está relacionado de alguna manera con los productos de Google.

Finalmente, resolví una pregunta que un maravilloso Google describió cuidadosamente e insertó en nuestra base de datos de preguntas. Ahora he consultado con antiguos colegas y me he asegurado de que la pregunta aún esté prohibida, por lo que definitivamente no se te preguntará en la entrevista. Lo presento en la forma en que me parece más efectivo, con una disculpa al autor original.

Pregunta

Habla sobre medir distancias. La mano es una unidad de medida de cuatro pulgadas comúnmente utilizada en países de habla inglesa para medir la altura de los caballos. Un año luz es otra unidad de medida igual a la distancia que recorre una partícula (¿u onda?) De luz en un cierto número de segundos, aproximadamente igual a un año terrestre. A primera vista, tienen poco en común entre sí, excepto que se usan para medir la distancia. Pero resulta que Google puede convertirlos con bastante facilidad:



Esto puede parecer obvio: al final, ambos miden la distancia, por lo que está claro que hay una transformación. Pero si lo piensas, es un poco extraño: ¿cómo calcularon esta tasa de conversión? Claramente, nadie realmente contó el número de manos en un año luz. En realidad, no necesitas tomar esto directamente. Simplemente puede usar conversiones conocidas:

• 1 mano = 4 pulgadas
  
• 4 pulgadas = 0.33333 pies
  
• 0.33333 pies = 6.3125e - 5 millas
  
• 6.3125e - 5 millas = 1.0737e - 17 años luz

El objetivo de la tarea es desarrollar un sistema que realice esta transformación. En particular:

En la entrada tiene una lista de factores de conversión (formateados en el idioma elegido) en forma de un conjunto de unidades iniciales de medida, unidades finales y factores, por ejemplo:

  ft 12
 yarda de pies 0.3333333
 etc. 

De modo que ORIGEN * MULTIPLICADOR = DESTINO. Desarrolle un algoritmo que tome dos valores unitarios arbitrarios y devuelva el factor de conversión entre ellos.

La discusión

Me gusta este problema porque tiene una respuesta intuitiva y obvia: ¡simplemente convierta de una unidad a otra, luego a la siguiente, hasta que encuentre el objetivo! No recuerdo a un solo candidato que se encontró con este problema y estaba completamente desconcertado sobre cómo resolverlo. Esto encaja bien con el requisito de un problema "más simple", ya que los anteriores generalmente requerían un estudio y una reflexión largos antes de encontrar al menos un enfoque básico de la solución.

Sin embargo, muchos candidatos no se dieron cuenta de su intuición como una solución de trabajo sin pistas obvias. Una de las ventajas de esta pregunta es que pone a prueba la capacidad del candidato para formular el problema (para enmarcar) para que se preste al análisis y la codificación. Como veremos, aquí hay una extensión muy interesante que requiere un nuevo salto conceptual.

Para el contexto, el encuadre es el acto de traducir un problema con una solución no obvia en un problema equivalente, donde la solución se deduce de forma natural. Si esto suena completamente abstracto e inexpugnable, lo siento, pero lo es. Explicaré a qué me refiero cuando presente la solución inicial a este problema. La primera parte de la solución será un ejercicio para desarrollar y aplicar conocimiento algorítmico. La segunda parte será un ejercicio de manipulación de este conocimiento para llegar a una optimización nueva y no obvia.

Parte 0. Intuición

Antes de profundizar, exploremos completamente la solución "obvia". La mayoría de las conversiones requeridas son simples y directas. Cualquier estadounidense que haya viajado fuera de los Estados Unidos sabe que la mayor parte del mundo usa la misteriosa unidad "kilómetro" para medir distancias. Para convertir, solo necesita multiplicar el número de millas por aproximadamente 1.6.

Nos hemos encontrado con tales cosas durante la mayor parte de nuestras vidas. Para la mayoría de las unidades, ya hay una conversión precalculada, por lo que solo debe verla en la tabla correspondiente. Pero si no hay conversión directa (por ejemplo, de manos a años luz), tiene sentido construir una ruta de conversión, como se indicó anteriormente:

• 1 mano = 4 pulgadas
  
• 4 pulgadas = 0.33333 pies
  
• 0.33333 pies = 6.3125e - 5 millas
  
• 6.3125e - 5 millas = 1.0737e - 17 años luz

¡Fue muy simple, se me ocurrió tal transformación usando mi imaginación y una tabla de transformación estándar! Sin embargo, quedan algunas preguntas. ¿Hay un camino más corto? ¿Qué tan preciso es el coeficiente? ¿La conversión es siempre posible? ¿Es posible automatizarlo? Desafortunadamente, aquí el enfoque ingenuo se rompe.

Parte 1. Decisión ingenua

Es bueno que el problema tenga una solución intuitiva, pero de hecho, esta simplicidad es un obstáculo para resolver el problema. No hay nada más difícil que tratar de entender de una manera nueva lo que ya entiendes, sobre todo porque a menudo sabes menos de lo que piensas. Para ilustrar, imagine que vino a una entrevista y que tiene este método intuitivo en su cabeza. Pero no permite resolver una serie de problemas importantes.

Por ejemplo, ¿qué pasa si no hay conversión ? El enfoque obvio no dice nada, es realmente posible convertir de una unidad a otra. Si me dan mil tasas de conversión, será muy difícil para mí determinar si es posible en principio. Si se me pide que haga una conversión entre unidades desconocidas (o inventadas) de un puntero y un jab , entonces no tengo idea por dónde empezar. ¿Cómo ayuda un enfoque intuitivo aquí?

Debo admitir que este es un tipo de escenario artificial, pero también hay uno más realista. Usted ve que mi declaración del problema incluye solo unidades de distancia. Esto se hace a propósito. ¿Qué sucede si le pido al sistema que convierta de pulgadas a kilogramos? Tanto usted como yo sabemos que esto no es posible porque miden diferentes tipos, pero la entrada no dice nada sobre el "tipo" que mide cada unidad.

Es aquí donde una formulación cuidadosa de la pregunta permite a los candidatos fuertes demostrar su valía. Antes de desarrollar el algoritmo, piensan en los casos extremos del sistema. Y tal declaración del problema les da a propósito la oportunidad de preguntarme si traduciremos diferentes unidades. Este no es un problema tan grande si ocurre en una etapa temprana, pero siempre es una buena señal cuando alguien me pregunta por adelantado: "¿Qué debería devolver el programa si la conversión no es posible?" Hacer la pregunta de esta manera me da una idea de las habilidades del candidato antes de que escriba al menos una línea de código.

Vista gráfica

Obviamente, el enfoque ingenuo no es adecuado, por lo que debemos pensar en cómo hacer tal conversión. La respuesta es considerar las unidades como un gráfico. Este es el primer salto de comprensión necesario para resolver este problema.

En particular, imagine que cada unidad es un nodo en un gráfico, y que hay un borde del nodo A al nodo B si A puede convertirse en B :



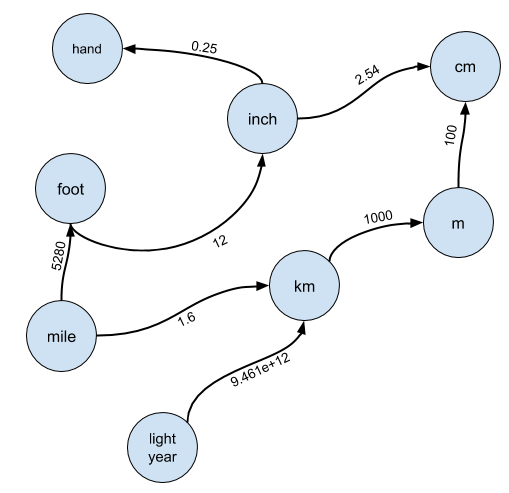
Los bordes están etiquetados con una tasa de conversión por la cual debes multiplicar A para obtener B

Casi siempre esperaba que el candidato presentara un marco así, y rara vez le daba pistas serias. Puedo perdonar al candidato que no se da cuenta de la solución al problema de usar conjuntos disjuntos o que no está muy familiarizado con el álgebra lineal para darse cuenta de una solución que se reduce a volver a elevar al poder de la matriz de adyacencia, pero los gráficos se enseñan en cualquier plan de estudios o curso de programación. Si el candidato no tiene el conocimiento apropiado, esta es una señal de "no contratación".

Como sea

Una representación gráfica reduce la solución al problema clásico de búsqueda de gráficos. En particular, dos algoritmos son útiles aquí: búsqueda amplia (BFS) y búsqueda profunda (DFS). Al buscar en ancho, examinamos los nodos de acuerdo con su distancia desde el origen:


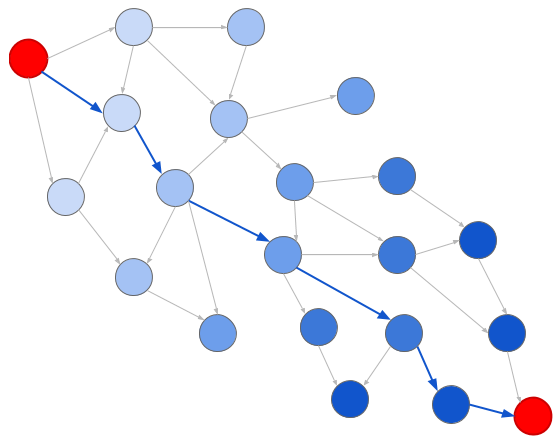El azul más oscuro significa generaciones posteriores

Y cuando buscamos en profundidad, examinamos los nodos en el orden en que ocurren:



El azul más oscuro también significa generaciones posteriores. Tenga en cuenta que en realidad no visitamos todos los sitios

Cualquiera de los algoritmos determina fácilmente si hay una conversión de una unidad a otra, es suficiente simplemente buscar en el gráfico. Comenzamos desde la unidad fuente y buscamos hasta encontrar la unidad de destino. Si no puede encontrar su destino (como si tratara de convertir pulgadas a kilogramos), sabemos que no hay manera.

Pero espera, falta algo. No queremos buscar una forma, ¡queremos encontrar una tasa de conversión! Aquí es donde el candidato debe dar el salto: resulta que puede modificar cualquier algoritmo de búsqueda para calcular la tasa de conversión simplemente guardando el estado adicional a medida que avanza. Ahí es donde las ilustraciones ya no tienen sentido, así que profundicemos en el código.

Primero, debe determinar la estructura de datos del gráfico, por lo que usamos esto:

 class RateGraph(object): def __init__(self, rates): 'Initialize the graph from an iterable of (start, end, rate) tuples.' self.graph = {} for orig, dest, rate in rates: self.add_conversion(orig, dest, rate) def add_conversion(self, orig, dest, rate): 'Insert a conversion into the graph.' if orig not in self.graph: self.graph[orig] = {} self.graph[orig][dest] = rate def get_neighbors(self, node): 'Returns an iterable of the nodes neighboring the given node.' if node not in self.graph: return None return self.graph[node].items() def get_nodes(self): 'Returns an iterable of all the nodes in the graph.' return self.graph.keys() 

Entonces comencemos con DFS. Hay muchas formas de implementarlo, pero, con mucho, la más común es una solución recursiva. Comencemos con esto:

 from collections import deque def __dfs_helper(rate_graph, node, end, rate_from_origin, visited): if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: rate = __dfs_helper(rate_graph, unit, end, rate_from_origin * rate, visited) if rate is not None: return rate return None def dfs(rate_graph, node, end): return __dfs_helper(rate_graph, node, end, 1.0, set()) 

En pocas palabras, este algoritmo comienza con un nodo, itera sobre sus vecinos e inmediatamente visita cada uno, haciendo una llamada recursiva a la función. Cada llamada de función en la pila guarda el estado de su propia iteración, por lo que cuando se devuelve una visita recursiva, su padre continúa inmediatamente la iteración. Evitamos visitar el mismo sitio nuevamente manteniendo un conjunto de sitios visitados en todas las llamadas. También calculamos el coeficiente asignando un factor de conversión entre cada nodo y la fuente. Por lo tanto, cuando nos encontramos con el nodo / bloque de destino, ya hemos creado el coeficiente de conversión del nodo de origen, y simplemente podemos devolverlo.

Esta es una gran implementación, pero adolece de dos fallas principales. En primer lugar, es recursivo. Si resulta que el camino deseado consiste en más de mil saltos, saldremos volando con una falla. Por supuesto, esto es poco probable, pero si hay algo inaceptable para un servicio a largo plazo, es un fracaso. En segundo lugar, incluso si completamos con éxito, la respuesta tiene algunas propiedades indeseables.

De hecho, ya di una pista al comienzo de la publicación. ¿Has notado cómo Google muestra la tasa de conversión de 1.0739e-17 , pero mi cálculo manual da 1.0737e-17 ? Resulta que todas estas multiplicaciones de coma flotante ya hacen pensar en difundir el error. Hay demasiados matices para este artículo, pero la conclusión es que debe minimizar la multiplicación de coma flotante para evitar errores que se acumulan y causan problemas.

DFS es un gran algoritmo de búsqueda. Si existe una solución, la encontrará. Pero carece de una propiedad clave: no necesariamente encuentra el camino más corto. Esto es importante para nosotros porque una ruta más corta significa menos saltos y menos errores debido a las multiplicaciones de coma flotante. Para resolver el problema, recurrimos a BFS.

Parte 2. Solución BFS

En esta etapa, si un candidato implementa con éxito una solución DFS recursiva y se detiene en ella, generalmente doy al menos una recomendación débil sobre la contratación de este candidato. Entendió el problema, eligió el marco apropiado e implementó una solución de trabajo. Esta es una decisión ingenua, por lo que no insisto en contratarlo, pero si se las arregló bien con otras entrevistas, no recomendaré negarse.

Vale la pena repetir esto: si tiene dudas, ¡escriba una solución ingenua! Incluso si no es completamente óptimo, la presencia de código en el tablero ya es un logro, y a menudo se puede encontrar la solución correcta sobre la base. Diré de manera diferente: nunca trabajes por nada. Lo más probable es que haya pensado en una solución ingenua, pero no quería ofrecerla, porque sabe que no es óptima. Si está listo para diseñar la mejor solución en este momento, está bien, pero si no, entonces registre el progreso realizado antes de pasar a cosas más complejas.

De ahora en adelante, hablemos sobre las mejoras al algoritmo. Las principales desventajas de una solución DFS recursiva son que es recursiva y no minimiza el número de multiplicaciones. Como veremos pronto, BFS minimiza el número de multiplicaciones, y también es muy difícil implementarlo de forma recursiva. Desafortunadamente, tendremos que abandonar la solución DFA recursiva, porque para mejorarla tendremos que reescribir completamente el código.

Sin más preámbulos, presento un enfoque iterativo basado en BFS:

 from collections import deque def bfs(rate_graph, start, end): to_visit = deque() to_visit.appendleft( (start, 1.0) ) visited = set() while to_visit: node, rate_from_origin = to_visit.pop() if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: to_visit.appendleft((unit, rate_from_origin * rate)) return None 

Esta implementación es funcionalmente muy diferente de la anterior, pero si se mira de cerca, hace más o menos lo mismo, con un cambio significativo: mientras DFS recursivo guarda el estado de la ruta adicional en la pila de llamadas, implementando efectivamente la pila LIFO, la solución iterativa la almacena en la cola FIFO

Esto implica la propiedad "ruta más corta / menor número de multiplicaciones". Visitamos los nodos en el orden en que ocurren, y de esta manera obtenemos generaciones de nodos. El primer nodo inserta a sus vecinos, y luego los visitamos en orden, pegándolos todo el tiempo y así sucesivamente. La propiedad de ruta más corta se deriva del hecho de que los nodos se visitan en el orden de su distancia desde la fuente. Por lo tanto, cuando encontramos un destino, sabemos que no hay una generación anterior que pueda conducir a él.

En este momento, casi hemos terminado. Primero debe responder algunas preguntas, y se ven obligados a volver a la formulación original del problema.

Primero, ¿lo más trivial si la unidad original no existe? Es decir, no podemos encontrar el nodo con el nombre dado. En la práctica, debe hacer algo de normalización de las cadenas para que la Libra, Libra y lb apunten al mismo nodo "libra" (o alguna otra representación canónica), pero esto está más allá del alcance de nuestra pregunta.

En segundo lugar, ¿qué pasa si no hay conversión entre las dos unidades? Recuerde que en los datos iniciales solo hay conversiones entre unidades, y no da ninguna indicación de si es posible obtener otro de una unidad en particular. Esto se reduce al hecho de que las transformaciones y las rutas son directamente equivalentes, por lo que si no hay una ruta entre dos nodos, entonces no hay transformación. En la práctica, terminas con islas de unidades no relacionadas: una para distancias, otra para pesos, otra para monedas, etc.

Finalmente, si observa de cerca el gráfico anterior, resulta que no puede convertir entre manos y años luz con esta solución. La dirección de las conexiones entre los nodos significa que no hay forma de pasar de la mano a años luz. Sin embargo, esto es bastante fácil de solucionar, porque las transformaciones se pueden revertir. Podemos cambiar nuestro código de inicialización del gráfico de la siguiente manera:

 def add_conversion(self, orig, dest, rate): 'Insert a conversion into the graph. Note we insert its inverse also.' if orig not in self.graph: self.graph[orig] = {} self.graph[orig][dest] = rate if dest not in self.graph: self.graph[dest] = {} self.graph[dest][orig] = 1.0 / rate 

Parte 3. Evaluación

Hecho Si el candidato ha llegado a este punto, lo más probable es que lo recomiende para contratarlo. Si estudió ciencias de la computación o tomó un curso de algoritmos, puede preguntar: "¿Es esto realmente suficiente para obtener una entrevista con este tipo?", A lo que responderé: "Esencialmente, sí".

Antes de decidir que la pregunta es demasiado simple, veamos qué debe hacer un candidato para llegar a este punto:

• Comprende la pregunta
  
• Construya una red de transformaciones en forma de gráfico
  
• Comprenda que los coeficientes se pueden comparar con los bordes del gráfico
  
• Vea la posibilidad de usar algoritmos de búsqueda para lograr esto.
  
• Elija su algoritmo favorito y cámbielo para seguir las probabilidades
  
• Si implementó DFS como una solución ingenua, reconozca sus debilidades.
  
• Implementar BFS
  
• Para dar un paso atrás y estudiar casos extremos:
  
  • ¿Qué pasa si nos preguntan sobre un nodo que no existe?
    
  • ¿Qué pasa si el factor de conversión no existe?
• Reconocer que las transformaciones inversas son posibles y probablemente necesarias

Esta pregunta es más fácil que las anteriores, pero también es difícil. Como en todas las preguntas anteriores, el candidato debe dar un salto mental de una pregunta formulada de manera abstracta a un algoritmo o estructura de datos que abre el camino a una solución. Lo único es que el algoritmo final está menos avanzado que en otros temas. Fuera de este material algorítmico, se aplican los mismos requisitos, especialmente con respecto a casos extremos y corrección.

“¡Pero espera!” Puedes preguntar. - ¿No está Google obsesionado con la complejidad del tiempo de ejecución? Ni siquiera preguntó sobre la complejidad temporal o espacial de este problema. ¡Oh bien! También puede preguntar: "Espere un minuto, le dio la calificación" muy recomendable para contratar "? ¿Cómo conseguirlo? Muy buenas preguntas, ambas. Esto nos lleva a nuestra ronda de bonificación extra final ...

Parte 4. ¿Es posible hacerlo mejor?

En este punto, me gustaría felicitar al candidato con una buena respuesta y dejar en claro que todo lo demás es solo una ventaja. Cuando la presión desaparece, podemos comenzar a crear.

Entonces, ¿cuál es la dificultad de ejecutar BFS? En el peor de los casos, debemos considerar cada nodo y borde individual, lo que da una complejidad lineal O(N+E) . Esto se suma a la misma complejidad de la construcción del gráfico O(N+E) . Para un motor de búsqueda, esto probablemente sea bueno: mil unidades de medida son suficientes para las aplicaciones más razonables, y hacer una búsqueda de memoria para cada consulta no es una sobrecarga.

Sin embargo, uno puede hacerlo mejor. Para motivar, considere cómo se inserta este código en la cadena de búsqueda. Las conversiones de algunas unidades no estándar son un poco más comunes, por lo que las calcularemos una y otra vez. Cada vez que se realiza una búsqueda, se calculan los valores intermedios, etc.

A menudo se sugiere simplemente almacenar en caché los resultados del cálculo. Cada vez que se calcula una conversión de unidad, siempre podemos agregar una ventaja entre las dos conversiones. Como beneficio adicional, obtenemos la transformación inversa, ¡y gratis! ¿Ya terminaste?

De hecho, esto nos dará un tiempo de búsqueda asintóticamente constante, pero costará el almacenamiento de bordes adicionales. En realidad, esto se vuelve bastante costoso: con el tiempo, buscaremos un gráfico completo, ya que todos los pares de transformaciones se calculan y almacenan gradualmente. El número de aristas posibles en el gráfico es la mitad del cuadrado del número de nodos, por lo que para mil nodos necesitamos medio millón de aristas. Por diez mil nodos, unos cincuenta millones, etc.

Yendo más allá del alcance del motor de búsqueda, para un gráfico de un millón de nodos, nos esforzamos por medio billón de bordes. Esta cantidad es simplemente irrazonable de almacenar, además pasamos tiempo insertando bordes en el gráfico. Debemos hacerlo mejor.

Afortunadamente, hay una manera de lograr un tiempo constante para buscar coeficientes, sin crecimiento de espacio cuadrático. De hecho, casi todo lo que necesitamos está justo debajo de nuestras narices.

Parte 4. Tiempo constante

Por lo tanto, el almacenamiento en caché total está realmente cerca de la solución óptima. En este enfoque, (en última instancia) obtenemos bordes entre todos los nodos, es decir, nuestra transformación se reduce a encontrar un borde. Pero, ¿es realmente necesario almacenar las conversiones de cada nodo a cada nodo? ¿Qué pasa si solo guardamos los factores de conversión de un nodo a todos los demás?

Eche otro vistazo a la solución BFS:

 from collections import deque def bfs(rate_graph, start, end): to_visit = deque() to_visit.appendleft( (start, 1.0) ) visited = set() while to_visit: node, rate_from_origin = to_visit.pop() if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: to_visit.appendleft((unit, rate_from_origin * rate)) return None 

Veamos qué sucede aquí: comenzamos desde el nodo fuente, y para cada nodo que encontramos, calculamos el coeficiente de conversión desde la fuente a este nodo. Luego, tan pronto como llegamos al destino, devolvemos el coeficiente entre los puntos inicial y final y descartamos los coeficientes intermedios.

Estas relaciones intermedias son clave. ¿Pero qué pasa si no los tiramos? ¿Qué pasa si los escribimos en su lugar? Todas las búsquedas más complejas e incomprensibles se vuelven simples: para encontrar la relación de A a B, primero encuentre la relación de X a B, luego divídala por la relación de X a A, ¡y listo! Visualmente, se ve así:


Tenga en cuenta que entre dos nodos no más de dos aristas

Resulta que para calcular esta tabla, casi no necesitamos cambiar la solución BFS:

 from collections import deque def make_conversions(graph): def conversions_bfs(rate_graph, start, conversions): to_visit = deque() to_visit.appendleft( (start, 1.0) ) while to_visit: node, rate_from_origin = to_visit.pop() conversions[node] = (start, rate_from_origin) for unit, rate in rate_graph.get_neighbors(node): if unit not in conversions: to_visit.append((unit, rate_from_origin * rate)) return conversions conversions = {} for node in graph.get_nodes(): if node not in conversions: conversions_bfs(graph, node, conversions) return conversions 

La estructura de transformación está representada por un diccionario de la unidad A en dos valores: la raíz del componente asociado de la unidad A y el coeficiente de conversión entre la unidad raíz y la unidad A. Como insertamos una unidad en este diccionario en cada visita, podemos usar el espacio clave de este diccionario como un conjunto de visitas en lugar de usar Un conjunto dedicado de visitas. Tenga en cuenta que no tenemos un nodo final, y en su lugar iteramos sobre los nodos hasta que hayamos terminado.

Fuera de este BFS, hay una función auxiliar que itera sobre los nodos en un gráfico. Cada vez que encuentra un nodo fuera del diccionario de traducción, inicia BFS a partir de ese nodo.Por lo tanto, tenemos la garantía de colapsar todos los nodos en sus componentes relacionados.

Cuando necesite encontrar la relación entre las unidades, simplemente usamos la estructura de transformación que acabamos de calcular:

 def convert(conversions, start, end): 'Given a conversion structure, performs a constant-time conversion' try: start_root, start_rate = conversions[start] end_root, end_rate = conversions[end] except KeyError: return None if start_root != end_root: return None return end_rate / start_rate 

La situación "no existe tal unidad" se maneja escuchando una excepción al acceder a la estructura de las transformaciones. La situación "no hay tales transformaciones" se maneja comparando las raíces de dos cantidades: si tienen raíces diferentes, entonces se detectan a través de dos llamadas BFS diferentes, es decir, están en dos componentes conectados diferentes y, por lo tanto, no hay manera entre ellos. Finalmente, realizamos la conversión.

Ahí tienes! La solución actual tiene una complejidad de preprocesamientoO(V+E)(no peor que las soluciones anteriores), pero también busca con tiempo constante. Teóricamente, duplicamos los requisitos de espacio, pero la mayoría de las veces ya no necesitamos el gráfico original, por lo que podemos eliminarlo y usar solo este. Además, la complejidad espacial es en realidad menor que el gráfico original: requiere O(V+E)porque necesita almacenar todos los bordes y vértices, y esta estructura requiere solo O(V)porque ya no necesitamos bordes.

Resultados

Si ha ido tan lejos, puede recordar que una de las preguntas fue originalmente para verificar si un problema más simple podría seguir siendo útil para elegir candidatos dignos y si podría dar una mejor idea de las habilidades. Me gustaría dar una respuesta científica definitiva, pero solo tengo historias de mi experiencia personal. Sin embargo, noté algunos resultados positivos.

Si dividimos la solución de este problema en cuatro obstáculos (discusión del encuadre, elección del algoritmo, implementación, discusión de la ejecución por un tiempo constante), al final de la entrevista casi todos los candidatos alcanzaron la "elección del algoritmo". Como sospechaba, la discusión sobre el encuadre era un buen filtro: los candidatos mostraban inmediatamente un gráfico o no podían acceder a él de ninguna manera, a pesar de las sugerencias significativas.

Esta es una señal útil de inmediato. Puedo entender cuando una persona no conoce estructuras de datos avanzadas u oscuras, porque seremos honestos, rara vez tiene que implementar conjuntos disjuntos. Pero los gráficos son una estructura de datos fundamental y se enseñan como parte de casi cualquier curso introductorio sobre este tema. Si el candidato tiene dificultades para comprenderlos o no puede aplicarlos fácilmente, probablemente sea difícil para él tener éxito en Google (al menos en mi tiempo allí, no sé cómo hoy).

Por otro lado, la elección del algoritmo no fue una fuente de señal particularmente útil. Las personas que pasaron por la etapa de encuadre generalmente llegaron al algoritmo sin ningún problema. Sospecho que esto se debe al hecho de que los algoritmos de búsqueda casi siempre se enseñan junto con los propios gráficos, por lo que si alguien está familiarizado con uno, entonces conoce el otro.

La implementación no fue fácil. Muchas personas no tuvieron problemas con la implementación recursiva de DFS, pero, como mencioné anteriormente, esta implementación no es adecuada para la producción. Para mi sorpresa, las implementaciones iterativas de BFS y DFS no parecen ser muy familiares para las personas, e incluso después de pistas obvias, a menudo surgieron en el tema.

En mi opinión, cualquiera que haya pasado por la fase de implementación ya me ha ganado la recomendación de "Contratar", y la discusión sobre el tiempo de entrega constante es simplemente una ventaja. Aunque analizamos la solución en detalle en el artículo, en la práctica, una discusión oral en lugar de escribir código suele ser más productiva. Muy pocos candidatos podrían tomar una decisión de inmediato. A menudo tenía que dar pistas sustanciales, e incluso entonces muchas personas no podían encontrarlo. Esto es normal: como se esperaba, una calificación altamente recomendada es difícil de obtener.

¡Pero espera, eso no es todo!

Básicamente, examinamos todo el problema, pero si está interesado en estudiarlo más a fondo, hay varias extensiones en las que no profundizaré. Dejo los siguientes ejercicios para el lector:

Primero, calentamiento: en la solución por el tiempo constante que presenté, elegí arbitrariamente el nodo raíz de cada componente conectado. En particular, uso el primer nodo componente que encontramos. Esto no es óptimo, porque para todos los valores conocidos elegimos algún nodo, aunque algún otro nodo puede estar más cerca del centro con rutas más cortas a todos los demás nodos. Su tarea es reemplazar esta elección arbitraria con una que minimice el número de multiplicaciones requeridas y minimice la propagación del error de coma flotante.

En segundo lugar, en todos los argumentos se supuso que todas las rutas iguales a través del gráfico son iguales inicialmente, lo cual no siempre es el caso. Una de las opciones interesantes para este problema es la conversión de divisas: los nodos son divisas, y las aristas de A a B y viceversa son los precios de oferta / demanda de cada par de divisas. Podemos reformular el tema de la conversión de unidades como una cuestión de arbitraje de divisas: implementar un algoritmo que, dado el gráfico de conversión de divisas, calcule un ciclo a través del gráfico que le dará al comerciante más dinero que la cantidad inicial. No incluya ninguna tarifa de transacción.

Finalmente, una verdadera joya: algunas unidades se expresan como una combinación de diferentes unidades base. Por ejemplo, un vatio se define en el sistema SI como kg • m² / s³. La tarea final es expandir este sistema para admitir la conversión entre estas unidades, teniendo en cuenta solo las definiciones de las unidades SI básicas.

Si tiene alguna pregunta, no dude en ponerse en contacto conmigo en reddit .

Conclusión

Cuando comencé a hacer esta tarea en las entrevistas, esperaba que fuera un poco más fácil que las anteriores. El experimento fue en gran medida exitoso: si el candidato vio de inmediato la solución, entonces usualmente hizo frente a la tarea rápidamente, por lo que tuvimos mucho tiempo para hablar sobre una solución avanzada con tiempo constante. Las personas que experimentaron dificultades, por regla general, tropezaron en otros lugares además del salto conceptual algorítmico: el candidato no pudo formular completamente el problema de una manera adecuada o esbozó una buena solución, pero no pudo traducirlo en un código de trabajo. No importa dónde o cuándo tuvieron dificultades, descubrí que podía obtener información significativa sobre las fortalezas y debilidades de los candidatos.

Espero que hayas encontrado útil este artículo. Entiendo que puede que no haya tantas aventuras con algoritmos como en algunos artículos anteriores. En las entrevistas a los desarrolladores, es costumbre discutir abundantemente los algoritmos. Pero la verdad es que surgen dificultades significativas cuando se utiliza incluso un método simple y conocido. Todo el código está en el repositorio de esta serie de artículos .