Solo división, o cómo crear una teoría matemática y ganar $ 400K con ella. Serie tres, final

En series anteriores, observamos números fraccionales desde varios ángulos inusuales. En esta serie, después de la introducción y algunas bases teóricas , intentaremos recopilar todo de forma conveniente y aprovechar la información disponible.

Búsqueda simple

Habiendo hablado sobre las propiedades de la tabla de residuos, podemos tratar de aplicar el conocimiento sobre la ganancia. Entonces, muchos en el mundo encuentran útil buscar números primos grandes. E incluso hay organizaciones listas para dar mucho dinero a alguien que encuentra un número primo grande. Pero el tema de la computación cuántica también es popular en el mundo. Por qué Porque promete hackear un sistema criptográfico conocido. Este, por así decirlo, es el eslogan publicitario de la computación cuántica, que permite convencer a cualquier gerente de toma de decisiones de asignar dinero para una lección tan interesante. Por lo tanto, también hablaremos sobre este tema.

Primero, le mostraremos cómo buscar números primos. El principal problema aquí es la cantidad. Para números grandes, simplemente no hay algoritmos que le permitan verificar rápidamente si hay un número primo frente a nosotros o uno compuesto. Por lo tanto, el tiempo de inactividad máximo para hoy es de menos de 25 millones de decimales de longitud. Esto es solo 10 megabytes, en tales matrices los procesadores modernos muestran tiempos de procesamiento de milisegundos, pero para verificar si hay un número primo en nuestra matriz, un procesador moderno consumirá electricidad y zumbará con un ventilador durante décadas. Es decir, técnicamente, el tamaño del procesador no es bueno, pero el número de operaciones en algoritmos conocidos para números tan grandes es simplemente enorme. ¿Por qué es esta situación?

Para las pruebas de simplicidad, por ejemplo, se utiliza la enumeración de divisores. Pero, ¿cuántos divisores necesitas iterar durante un número de diez megabytes de largo? La respuesta es que incluso los átomos con electrones en todo el universo serán suficientes solo para una pequeña parte de este valor. Es decir, necesitamos un gran número de universos, solo para colocar todos estos divisores allí. Demasiado? Por lo tanto, la enumeración de divisores para números de diez megabytes se aplica de forma limitada (sí, el universo nos decepcionó ...), pero afortunadamente existen otros algoritmos. Podemos distinguir algoritmos que no utilizan la enumeración de divisores y, al mismo tiempo, se garantiza que darán una respuesta, simple frente a nosotros o compuesta. Pero estos son algoritmos muy lentos. Es decir, ellos, por supuesto, son capaces de moler números de cien a doscientos bits de esa manera, pero diez megabytes para ellos es la muerte de una vez. Por lo tanto, tienes que salir de las formas difíciles.

Pero el problema con todos los trucos es que aún no han llegado a una teoría completa de la divisibilidad. Después de todo, si estuviera completo, encontraríamos rápidamente la respuesta, primo o no. Más precisamente, una teoría nos daría rápidamente un algoritmo de prueba que no nos mantendría esperando hasta la muerte térmica del universo. Es por eso que otorgan bonificaciones a aquellos que crean un algoritmo lo más rápido posible y, lo mejor de todo, una teoría completa para proporcionar algoritmos para todas las ocasiones.

Mientras tanto, tenemos a nuestra disposición una prueba específica de Luc-Lemer, que utiliza la conexión de números de Mersenne muy específicos con una secuencia determinada, pero no el resto de la división, como observamos recientemente, sino la suma de los grados de algunos números irracionales. Es decir, la prueba de simplicidad se hizo desde un lado, digamos, no del todo obvio, aunque algunos aquí pueden recoger comparaciones más complicadas. Pero, ¿por qué los grados de números irracionales resultaron estar más cerca de las pruebas de simplicidad que todos los otros logros de la teoría de números? Aparentemente porque las matemáticas no conocen soluciones simples. Y como resultado, se usó un método, aunque no es obvio pero sigue funcionando, desde la región no más cercana a los cálculos enteros, más o menos cómo la transición de coordenadas cartesianas a polares ayuda a usar métodos adicionales que son muy difíciles de implementar en coordenadas cartesianas.

Además de la prueba de Luc-Lemer, también hay pruebas probabilísticas. Ayudan a eliminar los números compuestos garantizados. Entonces, una de las pruebas probabilísticas utilizadas activamente es una prueba basada en la fórmula de Fermat, de la que hablamos recientemente. Como trabaja el Muy simple: ¿recuerda la columna de unidades a la derecha en la tabla restante? Este es un signo garantizado de simplicidad de número. Para explicar el cheque usando la fórmula de Fermat, los matemáticos usan una terminología específica que pocas personas entienden excepto por ellos, por lo que no entraremos en estas selvas matemáticas, sino que explicaremos todo con los dedos, o más bien, de la tabla de residuos. Para comprender cuál será el resto en la última columna, debe dividir por una columna y alcanzar el resto en la posición que contiene 1, o calcular este resto utilizando la fórmula que le permite obtener el resto por el número de posición y la base del sistema de números. La primera opción para números de diez megabytes requerirá un tiempo casi infinito, porque el ancho de la tabla es N-1, lo que significa que para un número del orden de un millón, la tabla tendrá al menos un millón de columnas. Por mil millones, mil millones. Por un billón, un billón. Pero un billón, son solo 12 decimales. Y estamos interesados ​​en un número en el que menos de 25 millones de caracteres. Incluso un billón de residuos por el método de dividir la columna, tenemos que calcular apenas menos de media hora, y esto es solo 12 decimales. Total! En comparación con 25 millones. ¿Crees que tienes tiempo suficiente para esperar el resultado de esta manera? Por eso es mejor calcular inmediatamente el valor deseado usando la fórmula. Y solo la fórmula de Fermat corresponde a la fórmula para calcular el resto en la última posición de la tabla. Además, si el período es más corto que el ancho de la tabla, las matemáticas aún no saben cómo calcularlo, lo que significa que, en cualquier caso, debemos elegir la última columna. Los matemáticos en la prueba simplemente verifican si el resto en la última columna es igual a uno para el sistema numérico que eligen (aunque los matemáticos no usan la noción de sistema numérico, para ellos solo hay una base elevada a una potencia). Si el resto no es igual a uno, se garantiza que el número sea compuesto. Como vimos en el ejemplo de la tabla para el número 21, es la ausencia de una unidad al final de muchas líneas lo que lo distingue de las tablas para números primos. Pero hay un problema. En algunas líneas, todavía puede haber unidades, que también podríamos verificar con el ejemplo de la tabla para 21. Es por eso que los matemáticos llaman a la prueba basada en la fórmula probabilística de Fermat. Es decir, no saben si el número es primo si la prueba de Fermat encontró un resto igual a uno, porque tales unidades falsas están en la tabla para el número 21, y en muchas otras tablas, incluso para números de diez megabytes. Por lo tanto, debe verificar todas las líneas seguidas, lo cual es muy largo, porque las líneas para un número de diez megabytes, como se señaló anteriormente, son mucho más que todo lo que conocemos en el universo, o simplemente decir: es probable que este número sea primo. Aquí está el último método y los matemáticos han elegido. Afortunadamente, hay pocas líneas que terminan con uno en la mayoría de los números compuestos. Es cierto que también están los llamados números de Carmichael, en los que todas las líneas, excepto los múltiplos de los divisores de dicho número, terminan en uno. Entonces, en los números de Carmichael, la prueba probabilística de la fórmula de Fermat está prácticamente garantizada que es incorrecta, porque para eliminar el error es necesario ingresar en un múltiplo del divisor, y diez megabytes de divisores pueden tener solo dos, y su valor puede ser muy grande, y por lo tanto la probabilidad de obtener está en una línea tal que, con una elección aleatoria de la base del sistema numérico, es prácticamente cero. Pero, por otro lado, los números de Carmichael son relativamente pequeños, lo que nos permite esperar una prueba probabilística. Solo cuando se buscan números primos, se excluye la esperanza de probabilidad. Es por eso que, después de seleccionar candidatos para los simples con la ayuda de las pruebas de probabilidad, se aplica la prueba Luc-Lemer.

Agregue un poco sobre los números de Carmichael. Son notables no solo por su capacidad de imitar a los simples. Entonces, la red tiene un sitio web donde puedes aprender diferentes secuencias de números . Si ingresa el número 561 (el número mínimo de Carmichael) en el campo de búsqueda, puede encontrar que participa en una gran cantidad de secuencias. ¿De qué está hablando esto? Aparentemente, sobre algunas propiedades estructurales aún desconocidas de números similares que son muy comunes en nuestro mundo. Hecho muy entretenido.

Pero volvamos a las pruebas de simplicidad. A pesar de un buen coeficiente de filtrado con pruebas probabilísticas, la humanidad pasa años buscando el próximo número primo máximo. Por qué Porque la dependencia del tiempo de ejecución de la prueba con el tamaño del número es cuadrática. Es decir, para números pequeños todo se dispara y no hay problemas, pero cuando los números aumentan un millón de veces, el tiempo para los cálculos aumenta un billón de veces. Por lo tanto, en un solo núcleo de procesador, consideraríamos la prueba de Luc-Lemer durante décadas. Pero incluso una prueba con la fórmula de Fermat, también consideraríamos lo mismo. Es decir, en ambos enfoques, el número de cálculos ha alcanzado los límites de las capacidades humanas. Tienes que hacer algo con esto, ¿no?

¿Cuáles pueden ser las alternativas a un desperdicio informático tan derrochador en el calentamiento del aire durante muchos años? Muy simple: debe predecir la simplicidad por la naturaleza del número, por su pertenencia a una clase en particular. Por lo tanto, los números de Mersenne se convirtieron en líderes en los tamaños alcanzados de números primos probados precisamente por su pertenencia a una clase específica. La prueba de Luke-Lemer funciona específicamente para una clase tan específica. Los números de otras clases están rezagados debido a la falta de una prueba tan costosa como la prueba de Luc-Lemer para números de diez megabytes (aunque para algunos, esta prueba está adaptada). Por lo tanto, necesitamos una clasificación de números que nos permita encontrar pruebas simples de simplicidad, así que Dios me perdone por ese juego de palabras.

¿Cómo crear tal clasificación? Tampoco es tan difícil: debe estudiar diferentes números e identificar características comunes entre ellos. En general, esto es exactamente lo que los matemáticos están tratando de hacer, pero hasta ahora no ha salido una flor de piedra. Por lo tanto, intentaremos ayudarlos.

El enfoque descrito anteriormente para analizar números basado en tablas de residuos esencialmente explora la divisibilidad de los números de la forma 1000 ... 000. Es decir, los ceros a la derecha se asignan constantemente a la unidad, multiplicándola por la base de cada uno de los sistemas numéricos presentes en la tabla restante. Como resultado del análisis, encontramos que diferentes números dividen los números de la forma 1000 ... 000 de diferentes maneras. Entonces los números primos generalmente no pueden dividir uno con ceros. Pero los componentes, e incluso, por ejemplo, de dos y cinco años, están completamente divididos. A continuación se muestra la tabla para el número 8:



Como puede ver, en él, en líneas que son múltiplos de 2, después de alguna entrada de residuos distintos de cero, solo queda uno ceros. Así es exactamente como se ven todos los números relacionados con la clase de divisores de unidades con ceros, y la presencia de ceros nos dice en qué sistemas numéricos tendremos éxito. Pero aquí está el problema: desde el punto de vista de encontrar números primos, una unidad con ceros no nos interesa en absoluto, porque se garantiza que se divide por la base del sistema de números, que nos da todos estos ceros después de uno. Entonces, necesitas estudiar la divisibilidad de otras clases de números. ¿Es lógico? Esto es exactamente lo que haremos.

¿Podemos probar la teoría de la divisibilidad?

Anteriormente, nos familiarizamos con las regularidades de las tablas restantes para la operación de división, que nos es relativamente familiar. Los patrones resultaron ser entretenidos, pero aún tienen el mismo problema: no nos dan un algoritmo rápido para verificar la simplicidad. Para tal prueba, nosotros, como en la prueba de acuerdo con la fórmula de Fermat, tendremos que elevar los números en un grado muy grande y luego encontrar el resto de dividir el resultado por el número en estudio. O simplemente repita todos los restos utilizando el método de "esquina" (antes de la muerte térmica del universo, por supuesto). Aquí están los datos: la operación de elevar a una potencia con la búsqueda del resto lleva 15 minutos en un núcleo para los números de pedido $$$2 ^ {100000}$ . Con un aumento en el tamaño del número en 1000 veces, obtenemos un aumento cuadrático (más logaritmos, pero esto no es tanto) al menos 1,000,000 de veces, pero en realidad, muchos millones de veces. Supongamos que, como resultado, tenemos un millón de horas para una prueba. Esto es aproximadamente 40,000 días o notablemente más de cien años. Si optimizamos la ejecución de la prueba hasta sus oídos, realícela teniendo en cuenta todas las características de la arquitectura del procesador, entonces quizás en lugar de cien años obtengamos 10. En 10 núcleos - 1 año. Por 1000 núcleos - 4 días. Pero esto es solo una prueba probabilística, porque hay máscaras como simples números compuestos. Entonces todavía necesita verificar dos veces. Pero lo más importante es el hecho de que el número de candidatos es de millones. Después de todas las posibles filtraciones, también habrá muchas. Por lo tanto, el mundo todavía está jugando con números de diez megabytes.

Pero tenemos una herramienta. La tabla restante también funciona para otros tipos de números. Por ejemplo, tome los números de Mersenne. En binario, es solo una secuencia de unidades. ¿Qué nos impide explorar una secuencia de unidades en lugar de una secuencia de ceros? Sí, nada lo impide. Y resulta que para tal secuencia, nuestro método funciona bastante bien y se conservan varios patrones previamente identificados. Aquí está el resultado para el número 7:



Como podemos ver, el número primo 7 en todos los sistemas numéricos (excepto los múltiplos de siete) es un divisor de números de Mersenne. Es decir, casi todas las líneas contienen un cero que nos informa sobre la divisibilidad de los números de la forma 111 ... 111 (en el sistema binario) por 7. Entonces, cuando trabajamos con el sistema de números binarios, vemos que el número 7 divide todos los números de Mersenne, la longitud que es un múltiplo de 3. Este resultado es obvio incluso sin una tabla restante: el número 7 en forma binaria consta de tres unidades (111), por lo que dividirá el número binario de tres unidades. Y si hay más unidades, la división se ve así:

111111 | 111 ------ 111 1001 111 111 111 

Es decir, simplemente ponemos siete (en forma binaria) debajo del dividendo. Y cuántas veces caben los siete, tantas unidades triples en un número divisible. Si en él el número de unidades no es un múltiplo de tres, entonces dicho número no es divisible por 7. Pero todo esto es obvio siempre que estudiemos números con una estructura idéntica (7 y 63, como en el ejemplo). Y si la estructura de los números es más complicada, una tabla de residuos nos ayudará. Entonces, para todos los simples obtenemos un resultado similar, pero con un período de división ligeramente más largo. A continuación se muestra un ejemplo del número 11 (el número ya está en decimal):



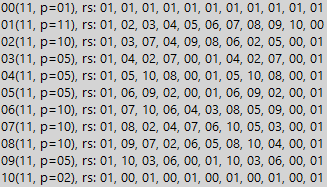
Vemos que en el sistema binario la distancia a cero (período de divisibilidad) para el número 11 es 10. Es decir, cualquier número de Mersenne que contenga 10k unidades, donde k es un número entero mayor que cero, es necesariamente divisible por 11. Se puede demostrar fácilmente que el resto son simples los números se comportan exactamente igual, excepto por el tamaño del período, por supuesto. Pero para el compuesto, la situación es nuevamente menos armoniosa. A continuación vemos un ejemplo para el número 8:



Aparentemente, 8 no puede dividir los números de Mersenne en forma binaria. Aquí en el ternario, por favor, pero los números de Mersenne consisten en unidades solo en forma binaria. La situación es similar con otros números compuestos: tienen todo de diferentes maneras. La imagen esbelta y simétrica para los números primos no se repite para los compuestos. Pero para nosotros es precisamente lo simple lo que importa, porque si el número se divide en un primo, entonces no hay absolutamente ningún problema si también se dividirá en un compuesto que incluya este simple. Pero si el número no se divide en uno simple, entonces será imposible dividirlo en un compuesto con uno tan simple. Entonces, deberíamos estar interesados ​​solo en los números primos.

Ahora resumamos. Sabemos que los números de Mersenne se dividen en números primos y que para la divisibilidad, los números de Mersenne necesitan una cantidad de unidades que sea un múltiplo del período de divisibilidad del número en estudio. Pero también sabemos que los candidatos para los números primos de Mersenne son solo aquellos en los que el número de unidades también es un número primo. Es decir, esta cantidad no se divide en nada más que una unidad y en sí misma. De ahí la conclusión: necesitamos un número primo cuyo período de divisibilidad sea igual a la longitud del número de Mersenne. Si durante algún tiempo del número de Mersenne no encontramos un divisor con un período adecuado, tenemos ante nosotros un número primo de Mersenne. Parece simple

Pero comienzan otras dificultades. ¿Cómo encontrar un número cuyo período coincida con la longitud del número de Mersenne? Para responder a esta pregunta, debe resolver una tarea modesta: encontrar una manera por medios simples para averiguar el período de un número primo arbitrario. Por ahora, solo podemos compartir una esquina o empujar en algún lugar específico usando una fórmula con grandes grados. Pero si pudiéramos calcular el período sin la necesidad de cálculos largos, encontraríamos rápidamente el divisor correcto o nos aseguraríamos de que no haya ninguno en la naturaleza. Exactamente la misma tarea modesta nos espera en el caso del estudio de la divisibilidad de los números de la forma 1000 ... 000. Por lo tanto, el período de divisibilidad es muy importante en todos los aspectos.

¿Cómo encontrar un período?

Aquí, las computadoras cuánticas corren en nuestra ayuda. Érase una vez, en algún momento inmemorial, un cierto conocedor de la física cuántica con el nombre de Shor, sugirió encontrar el período precisamente con la ayuda de una computadora cuántica. De hecho, una computadora cuántica solo da un valor intermedio, del cual una computadora ordinaria recibe un período, pero el punto no es ese, sino que sin una computadora cuántica, las matemáticas no pueden calcular el período. Pero al calcular el período, tenemos la oportunidad de calcular con precisión el valor del resto estrictamente en la mitad del período. ¿Por qué se necesita esto? Por el hecho de que puede obtener factores que necesariamente contienen un cierto valor que es un múltiplo del divisor del número en estudio. Esto se hace sumando al resto de la unidad y restando la unidad. Los dos números resultantes se pueden omitir a través de un algoritmo rápido para encontrar el divisor común más grande con el número en estudio. En al menos un caso, obtenemos el divisor del número bajo investigación. Es cierto, no todo es tan perfecto, porque como vimos en el ejemplo de la tabla para números primos, en el medio de la fila a menudo hay una adición al número que se está investigando (N-1), de esta forma obtenemos:

$$

$$N-1 + 1 = N$$

$$

$$N-1-1 = N-2$$

De ello se deduce que en un caso tenemos el número estudiado en sí mismo, y no tiene sentido calcular el máximo factor común, y en el segundo caso, hemos garantizado que no tiene divisores comunes con el número estudiado. No hay divisores comunes porque este número es solo 2 menos que el número investigado, lo que significa que no importa qué número se ajuste al número entero estudiado varias veces (sería su divisor), restándolo del número estudiado obtenemos un menor garantizado valor que $$$N-2$ , o usando las fórmulas:

$$

$$N / x = k$$

$$

$$(N-x) / x = k-1$$

$$

$$N-x <N-2 \ Flecha derecha x> 2 \; \ & \; (N-2) / x \ ne m$$

Aquí N es un número de prueba impar (impar porque un múltiplo de dos es divisible por dos, y no necesitamos dividirlo por nada), x es un divisor de N, k es el resultado total de la división $$$N / x$ , m es todo el resultado de la división $$$(N-2) / x$ . Es decir, a veces tenemos que cambiar el sistema de números y pedirle a la computadora cuántica que encuentre un nuevo período, con la esperanza de que en el medio haya un número más adecuado. Una limitación más es la paridad obligatoria del valor de duración del período. Pero esto no es tan aterrador, porque en cualquier caso, una computadora cuántica calculará la longitud que necesitamos (o varias longitudes) mucho más rápido que la muerte térmica del universo, a diferencia de otros algoritmos.

Aunque calcular el período para obtener divisores de números es una tarea ligeramente diferente de encontrar simples. Sin embargo, podemos agregar algo aquí usando las tablas sobrantes. Por lo tanto, las tablas muestran que la mitad de las filas de longitud par suele ser un número que cumple la siguiente condición:

$$

$$r ^ 2 \ pmod N = 1$$

Aquí r es el resto deseado, y N es el número bajo investigación. Por lo tanto, resulta que no hay necesidad de buscar un período para obtener divisores de un número, porque se busca un período para encontrar el resto r, y luego sumar y restar uno. Es decir, puede encontrar inmediatamente este resto que satisfaga la condición anterior. Es cierto que la búsqueda de este valor tampoco es trivial. ¿Pero tal vez una computadora cuántica puede ser encarcelada por tal cosa? Los expertos en computación cuántica necesitan comprender cuántos qubits se necesitan para esto (los qubits son esos loros que miden la "potencia" de una computadora cuántica). Aunque, tal vez, puedas prescindir de una computadora cuántica. Para hacer esto, solo necesita comprender qué patrones serán útiles. Algunos de los patrones son visibles en las tablas de residuos, pero el resto de los lectores tendrán que resolverlos por su cuenta, y luego definitivamente descifrará la criptografía basada en RSA. Es cierto, hay un par de dificultades: primero necesita encontrar estos patrones útiles, bueno, y luego ... Luego, es posible que no le paguen dinero. Primero, los premios se otorgan por números primos grandes, no por piratear RSA. Y en segundo lugar, bueno, piense usted mismo cuántas organizaciones serias en el mundo están interesadas en interceptar los datos de otras personas de esta manera. Y algunos FSB (CIA, Mossad, Mi-5, solo la mafia) descubrieron que sabes algo. ¿Adivina qué te pasará? Por lo tanto, usted actúa únicamente bajo su propio riesgo y riesgo.

Es cierto que el tema cuántico en sí es bastante interesante porque contiene incertidumbre cuántica, fluctuaciones de vacío y otros darwinismos cuánticos. ¿Cómo se puede explicar todo esto? Para ser sincero, no lo sé, pero veo una analogía con las tablas restantes. Por ejemplo, cuando alguien observa los valores en la tabla residual y no conoce los patrones mencionados anteriormente, entonces para él solo hay algo de ruido en la tabla donde los números se cambian entre sí de manera aleatoria, como algunas fluctuaciones en el vacío. Pero si comprende que solo estamos aplicando el mismo algoritmo a diferentes pares de "secuencia - número bajo investigación", entonces toda esta papilla hirviendo de los números instantáneamente se vuelve comprensible. Y de la misma manera, queda claro por qué, entre el gran conjunto de valores posibles para llenar la tabla, solo quedan estrictamente definidos los valores estrictamente definidos. Pero hasta que obtengamos la "interacción" de la secuencia con el número estudiado, no podemos predecir el contenido de la tabla. Más precisamente, cualquier relleno será igualmente probable. Pero después de la "interacción", todo se volverá estrictamente lógico, de lo igualmente probable nacerá una sola probabilidad para una sola opción. Y no porque cierto darwinismo funcione, sino solo por la aplicación de cierto algoritmo a datos de entrada específicos. Si no conoce el algoritmo, puede parecer que las filas de la tabla son de estilo Darwin. Y si lo sabes, todo es muy simple. ¿Quizás en la física cuántica es necesario buscar no solo partículas, sino también un algoritmo para su "división"?

Y nuevamente sobre el período

Sin embargo, el período es muy importante para nosotros. Sí, así es como le responderán en la línea directa sobre los problemas candentes de las matemáticas. Como se muestra arriba, el conocimiento del período permite comprender si un número tiene divisores o, de otra manera, si es primo. Por lo tanto, continuamos sobre el período. Hasta ahora, conocemos varias propiedades de período (unicidad de valores, simetría con una longitud par, etc.), pero no sabemos cómo determinar su longitud. Aunque hay un límite superior e inferior: el período no puede ser más largo que el número bajo investigación menos uno, y tampoco puede ser más corto que el período de crecimiento de la base del sistema numérico hasta que se exceda el número en estudio (para siete es 3, para 11 es 4, etc. .). Puede intentar aplicar las leyes conocidas de las tablas estudiadas y derivar otras nuevas, pero hasta ahora hay bastantes instrucciones aquí, la mayoría de las cuales no conducen al éxito, aunque hasta que pruebe cada una, no lo sabrá.

Por lo tanto, la forma más prometedora es crear una teoría mejorada de la divisibilidad. En base a las secuencias características de los residuos, es posible revelar las leyes de divisibilidad de muchas clases de números. Hasta ahora, solo se han mostrado dos clases (números de Mersenne y números iguales a los grados del sistema de números), pero en realidad hay un número infinito de ellos. ¿Cómo procesar el conocimiento en todas las clases de números? Solo en trabajo paralelo masivo, y no en forma de calentadores de aire de hierro, sino en forma de personas que trabajan juntas en una tarea tan grande. El resultado ideal sería la creación de una teoría general de la divisibilidad de todas las clases de números. Esto es para empezar, y luego desaparecerá la divisibilidad de los polinomios y otros álgebra. ¿Pero deberíamos esperar una concentración tan maravillosa de mentes humanas sobre la tarea de encontrar números primos? Sospecho que no. Por lo tanto, lamentablemente, nuevamente necesitamos otras formas.

Teóricamente, existe tal forma

Si estudiamos secuencias divisibles alternativas, que incluyen valores diferentes, encontramos que el período de división de tales secuencias aumenta un múltiplo de la longitud de los fragmentos repetidos de las secuencias. A continuación se muestra un ejemplo de una secuencia divisible de la forma 1010 ... 1010, donde cero y uno cambian periódicamente. La secuencia dada siempre se divide en la base del sistema de números, pero en este caso, la simplicidad del ejemplo de estudiar los números de la clase periódica es importante solo para nosotros, por lo que no prestamos atención a la divisibilidad por construcción.





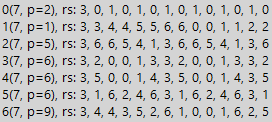
Aquí vemos dos tablas para el número 7 y la secuencia anterior, una es normal y la segunda tabla se multiplica por 3. De los patrones previamente identificados en este ejemplo, hay aún menos, pero, sin embargo, para los sistemas de números en las bases 1 y 6, vemos aumentar la duración del período a $$$2 * N-2$ . Y para multiplicado por 3 tablas, vemos una pérdida de divisibilidad para las bases de los sistemas numéricos 2 y 5, lo cual es bastante entretenido en sí mismo (la propiedad de divisibilidad ha cambiado de la multiplicación). Pero más importante que eso. Es importante comprender la posibilidad de aplicar tablas de divisibilidad a cualquier secuencia. Pero, ¿por qué necesitamos alguna secuencia? Por ejemplo, para aumentar el período mínimo de divisibilidad.

Si el período mínimo puede alargarse, esto nos permite proceder simplemente a la construcción de números primos. Sí, los números primos no pueden calcularse, sino construirse matemáticamente. Cuando el período es largo, un número pequeño divide uno grande, lo que significa que si todos los números tienen períodos grandes, para los números grandes los divisores solo pueden ser números pequeños. Que da Esto hace posible encontrar todos los divisores de un gran número mediante una simple búsqueda. Dado que los números pequeños dividen los números grandes, el tamaño de estos números pequeños ayuda a nuestras computadoras a resolver el problema que no pueden resolver con divisores grandes. Por lo tanto, la dirección adicional de la búsqueda de números primos se vuelve clara: necesitamos encontrar una secuencia que nos proporcione períodos mínimos grandes. ¿Por qué el mínimo? Debido a que todavía no sabemos cómo calcular un período sin enumerar todos los residuos o elevar a una potencia, y por lo tanto no podemos simplemente encontrar un período suficientemente largo si es mayor que el mínimo, bueno, sabemos el período mínimo simplemente por el análisis de las tablas restantes, es decir, no necesitamos calcularlo . Bueno, cuando encontramos la secuencia que necesitamos (y solo para esto podemos usar el análisis de muchas clases de tales secuencias), simplemente seleccionamos la longitud de la secuencia que no se ajustará a ninguno de los períodos mínimos que conocemos. Es decir, recogeremos un número tan grande, que obviamente no tiene divisores. Y si su tamaño es grande, nos espera un premio. Al mismo tiempo, no nos interesarán más que los períodos mínimos, porque ya dividen números muy grandes, a los que llegaremos más adelante.

Todo lo que queda es encontrar la secuencia correcta. ¿Quién lo tomará? Pero incluso si no lo encontramos, entonces, para el cifrado mencionado anteriormente, trabajar con secuencias alternativas permitirá agregar otro término al cifrado que aumente la fuerza criptográfica; ahora los descifradores deberán adivinar la secuencia que hemos elegido, que puede ser infinita en número. Además, para generar secuencias pseudoaleatorias, obtenemos la repetibilidad de los valores en la serie de residuos, y no solo en la serie del período de fracción.

Y finalmente, ¡los premios!

Electronic Frontier Foundation está listo para pagarle a cualquiera primero $ 150k, y luego otros $ 250k. En total - $ 400k . ¿No te molestaría eso? Entonces al punto! Pero la cosa es simple: necesitas encontrar un número primo de cien millones de decimales. Esto es aproximadamente 300 millones de bits, o 40 megabytes. Solo queda por superar el récord actual 4 veces. Y luego necesitas mil millones de dígitos decimales de largo. Esto ya es de 400 megabytes. Y todo, por dos números: 400 mil dólares verdes para siempre.

De hecho, estas no son figuras tan terribles. Ahora, si pudiéramos evitar calcular el resto de la división de grandes grados por el número en estudio ... Para secuencias simples de la forma 100 ... 00 y 111 ... 111, el grado está necesariamente presente. ¿Pero tal vez hay secuencias para las cuales la fórmula para calcular el i-ésimo miembro de una serie de residuos será más simple? O realmente puede encontrar una secuencia con un período mínimo grande. Después de todo, ¿qué período necesitamos? Solo 300 millones (en forma binaria). Si cierta secuencia nos da un período mínimo de la forma 100 * N, donde N es el número bajo investigación, entonces hasta 3 millones de números serán suficientes para que podamos encontrar un número de 150k $. Y hasta 30 millones por un número de $ 250k. Y ahora, cuando puede pasar un período corto en un número muy grande (para las secuencias 100..00 y 111 ... 111), no tenemos ninguna posibilidad simple de encontrarlo. Pero hay esperanza y todo depende de la elección exitosa de la dirección de la búsqueda. Iterar las secuencias de una en una aparentemente no es realista para una persona, pero puedes probar la multitud.

Bueno, cuando encuentras los números requeridos, te espera una pequeña burocracia. Primero tendrá que publicar un artículo en una revista matemática en los EE. UU. O Inglaterra o Canadá o Australia, y la revista debe pertenecer a la lista indicada por la Electronic Frontier Foundation (EFF) (estas son revistas de buena reputación). En el artículo, debe demostrar que su método realmente hace posible encontrar el número primo deseado. Luego, envía una carta de felicidad al EFF (a una dirección específica), donde señala el artículo publicado y luego espera las órdenes del EFF. Los pedidos pueden estar relacionados con verificar todo lo que hizo para encontrar el número. No debe haber secretos ni acciones ilegales o dudosas. Y eso es todo, después de eso, tu premio.

¿Qué emboscadas te pueden esperar en tu camino? Bueno, para empezar, para encontrar un número primo y no cometer errores al buscarlo. A continuación, debe escribir en un diario sólido. Como la revista es sólida, la reacción habitual de los editores a la carta del próximo inventor de la máquina de movimiento perpetuo es esta:

- que? Otro monstruo? A la canasta!

Pero es posible que tenga experiencia en la redacción de artículos y que pueda hacer frente fácilmente a este problema. Y luego encontrarás un cheque. No sé cuál será su evidencia estudiada por EFF, pero escriben que pueden estar interesados ​​en todo, cualquier cosa. Será especialmente interesante si los objetivos del FEP no coinciden con el resultado que proporciona. Por lo tanto, declaran el objetivo de desarrollar métodos para usar computadoras personales para ponerlas en uso remoto temporal para computación de terceros.El premio anterior se otorgó solo por la creación y promoción del programa, que los voluntarios descargaron y, por lo tanto, proporcionaron los terrenos necesarios para obtener números primos. Cómo se relaciona EFF con el cálculo de una prima sin terraflops masivos, no lo sé. Teóricamente, no hay restricciones en sus requisitos, por lo que el éxito es completamente posible.

Eso es todo, después de pasar por las dos etapas indicadas (y sin olvidar encontrar los números necesarios en la etapa cero), usted indica el banco y el número de cuenta donde le corresponde el premio. Una gran suma Usted maneja el impuesto a su propio costo.

En lugar de un epílogo

Érase una vez, Pierre Fermat, que no era matemático, descubrió muchos patrones para la teoría de números. El hombre se preguntaba, bueno, había tiempo libre disponible. Y aquí tienes los logros que aún se recuerdan. Otro ejemplo es Evarist Galois. Estudió matemáticas a la edad de 16 años, y a los 20 años murió en un duelo. Durante 4 años trató de interesar a muchos matemáticos con sus hallazgos, pero no tuvo éxito. Sin embargo, después de la muerte, su trabajo fue apreciado y es a ellos a quienes debemos la creación de una rama de las matemáticas como la teoría de grupos, así como el desarrollo del álgebra. Una vez más, fue interesante para una persona encontrar las estrellas, pero organizar los trabajos de acuerdo con las reglas no era para él. Pero afortunadamente, su trabajo fue formalizado por otros. Y otro ejemplo: George Cantor, reflexionando sobre los conceptos bien conocidos del conjunto y su elemento, dedujo la teoría a fines del siglo XIX,que destacados matemáticos acordaron considerar dignos de convertirse en la base de la reina de las ciencias.

¿Por qué todas estas historias? Como solía decir el Sr. Obama, "¡Puedes!" Sí, este eslogan estadounidense es muy adecuado para personas entusiastas. A pesar del desarrollo de la ciencia en la actualidad, no está completo, no es perfecto y hay lugares en los que el pie de un verdadero científico no ha pisado. Así que encienda nuestra curiosidad e intentemos buscar caminos sin trabas, y ¿qué pasa si tiene éxito?