La nueva prueba resuelve la aproximación de números como pi

Los antiguos griegos estaban interesados ​​en si es posible expresar aproximadamente números irracionales en fracciones. Para probar la antigua hipótesis de Duffin-Schaffer , dos matemáticos dieron una respuesta exhaustiva.

La notación binaria π es infinita. Pero un número infinito de fracciones puede acercarse a este número con una precisión cada vez mayor.

Las inmersiones profundas en la recta numérica no son tan inexpugnables como podría parecer. Esta es una de las consecuencias de la nueva evidencia significativa de cómo los números complejos se prestan a aproximaciones simples.

La prueba resuelve el problema de hace casi 80 años, conocido como la hipótesis de Duffin-Shaffer. Por lo tanto, da una respuesta final que ha ocupado a los matemáticos desde la antigüedad: ¿bajo qué condiciones es posible representar números irracionales que duran infinitamente largos, como pi, con fracciones simples del tipo 22/7? La prueba establece que la respuesta a esta pregunta bastante general se encuentra como resultado de un solo cálculo.

"Hay un criterio simple para determinar si puedes aproximar casi cualquier número o prácticamente ningún número", dijo James Maynard de la Universidad de Oxford, coautor de la prueba que hizo con Dimitris Cuculopoulos de la Universidad de Montreal.

Los matemáticos han estado sospechando durante varias décadas, este criterio simple es clave para entender cuándo se puede obtener una buena aproximación, pero no pudieron probarlo. Cuculopoulos y Maynard pudieron hacer esto solo después de reformular este problema de números en términos de las conexiones entre puntos y líneas del gráfico, un cambio cardinal en perspectiva.

"Diría que tenían la confianza suficiente (y eso obviamente estaba justificado) para tomar el camino elegido", dijo Jeffrey Waaler, de la Universidad de Texas en Austin, quien participó en los primeros resultados relacionados con la hipótesis de Duffin-Schaffer. "Gran trabajo".

Éter aritmético

Con números racionales, todo es simple. Incluyen números para contar objetos y todos los demás números que se pueden escribir en fracciones.

Debido a esta capacidad de anotarse, los números racionales nos son más conocidos. Sin embargo, entre todos los números reales, los racionales son realmente muy pocos. La mayoría de los números son irracionales , con notación decimal infinita, y no se pueden escribir en fracciones. Algunos de ellos resultaron ser lo suficientemente importantes como para merecer una notación simbólica: pi, e, √2. El resto ni siquiera puede ser llamado. Están en todas partes, pero son inalcanzables, como un éter aritmético.

Quizás, por lo tanto, será natural pensar: si no podemos expresar con precisión los números irracionales, ¿qué tan cerca podemos llegar a ellos? Esta es un área de aproximación racional. Los matemáticos de la antigüedad se dieron cuenta de que la esquiva relación de circunferencia a diámetro puede aproximarse bastante bien usando la fracción 22/7. Más tarde, los matemáticos descubrieron una aproximación comprimida aún más precisa y casi la misma a pi: 355/113.

"Escribir pi es muy difícil", dijo Ben Green de Oxford. "La gente trató de encontrar la aproximación más precisa a pi, y una de las formas comunes de hacerlo era usar números racionales".



En 1837, el matemático Peter Gustav Lejeune de Dirichlet descubrió una regla que nos dice con qué precisión se pueden aproximar los números irracionales usando números racionales. La aproximación es fácil de encontrar si no establece el valor exacto del error. Pero Dirichlet demostró la existencia de una relación clara entre fracciones, números irracionales y los errores que los separan.

Probó que para cualquier número irracional hay infinitas fracciones que se le acercan cada vez más. Más precisamente, el error de cada fracción no será más de 1 dividido por el cuadrado del denominador. Por ejemplo, la fracción 22/7 expresa aproximadamente pi con una precisión de 1/7 ² , o 1/49. La fracción 355/113 no está más lejos de pi que 1/113 ² , o 1/12 769. Dirichlet demostró que hay infinitas fracciones, acercándose cada vez más a pi con un denominador creciente.

"Una cosa sorprendente y notable es la capacidad de expresar aproximadamente un número real a través de una fracción, con un error que no exceda uno dividido por el cuadrado del denominador", dijo Andrew Granville, de la Universidad de Montreal.


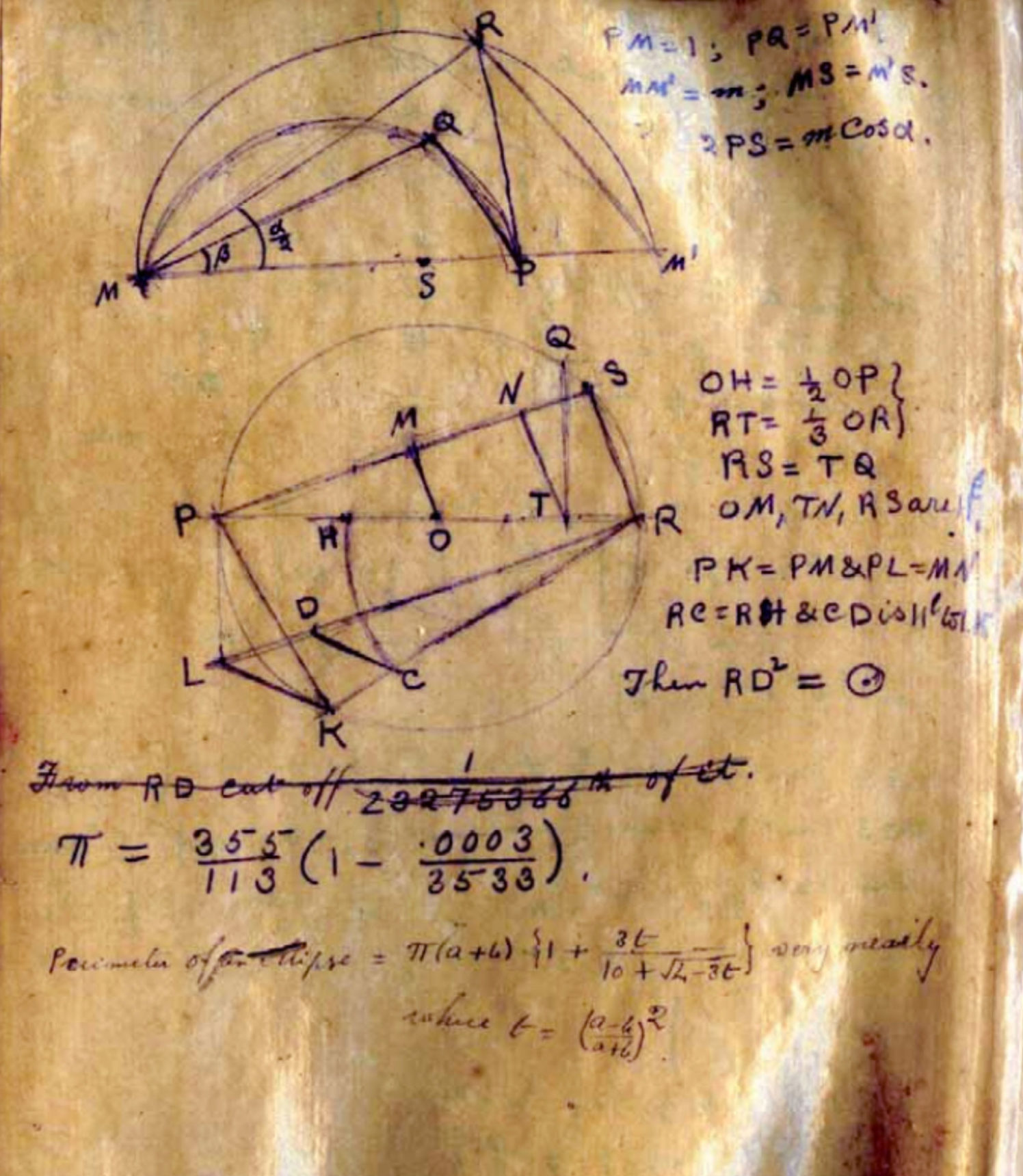En el manuscrito de 1913, el matemático Srinivasa Ramanujan Iyengor utilizó la fracción 355/113 como una aproximación racional de pi.

El descubrimiento de Dirichlet fue una afirmación limitada sobre la aproximación racional. Dice que para cualquier número irracional puedes encontrar infinitas fracciones acercándose a él, si puedes usar cualquier número entero como denominador, y estás satisfecho con el error en el tamaño de su cuadrado inverso. Pero, ¿qué sucede si desea que los denominadores pertenezcan a algún subconjunto (infinito) de enteros, por ejemplo, al conjunto de primos o al conjunto de cuadrados completos ? ¿Qué sucede si desea que el error de aproximación sea 0.00001 o que tenga algún otro valor? ¿Serás capaz de encontrar infinitas fracciones aproximadas precisamente en tales condiciones?

La hipótesis de Duffin-Shaffer es un intento de crear la plataforma más generalizada para trabajar con aproximaciones racionales. En 1941, los matemáticos R.D. Duffin y A.S. Schafer presentó el siguiente escenario. Primero, elija una lista interminable de denominadores. Puede ser todo lo que desee: números impares, números divisibles por 10, números primos.

Luego, para cada número de la lista, seleccione con qué precisión necesita aproximar el número irracional. La intuición nos dice que si elegimos errores suficientemente grandes, tendremos más oportunidades de aproximación. Si elige un tamaño de error pequeño, será más difícil. "Cualquier secuencia servirá si queda suficiente espacio", dijo Kukulopoulos.

Ahora, dados los parámetros seleccionados, una secuencia de números y un cierto error, surge la pregunta: ¿es posible encontrar infinitas fracciones que se aproximen a todos los números irracionales?

La hipótesis proporciona una función matemática para evaluar esta pregunta. Sus parámetros actúan como entrada. El resultado puede ser una de dos opciones. Duffin y Schaffer sugirieron que estas dos opciones corresponden precisamente a si su secuencia puede aproximar casi todos los números irracionales con la precisión requerida, o prácticamente ninguno de ellos (se menciona "prácticamente" porque para cualquier conjunto de denominadores siempre habrá un número pequeño números irracionales aislados que pueden o no pueden aproximarse lo suficientemente bien).

“Obtienes casi todo o casi nada. No hay opciones intermedias ”, dijo Maynard.

Esta fue una declaración extremadamente general, tratando de caracterizar la aproximación por números racionales a lo largo y ancho. El criterio propuesto por Duffin y Schaffer parecía correcto para los matemáticos. Sin embargo, para demostrar que la salida binaria de la función contiene todo lo que necesita para comprender si su aproximación funciona o no, fue mucho más difícil de hacer.

Doble recuento

La prueba de la hipótesis de Duffin-Schaffer es comprender qué beneficio obtiene de cada uno de los denominadores disponibles para usted. Para sentir esto, será útil considerar una versión más pequeña de esta tarea.

Suponga que desea aproximar todos los números irracionales en un segmento del 0 al 1. Imagine que todos los números naturales del 1 al 10 están disponibles como denominadores. La lista de fracciones posibles es bastante grande. Primero 1/1, luego 1/2 y 2/2, luego 1/3, 2/3 y 3/3, y así sucesivamente, hasta 9/10 y 10/10. Sin embargo, no hay beneficio de ellos.

Por ejemplo, 2/10 es lo mismo que 1/5, y 5/10 es lo mismo que 1/2, 2/4, 3/6 y 4/8. Antes de la aparición de la hipótesis de Duffin-Schaffer, el matemático soviético Alexander Y. Khinchin formuló una hipótesis de una aproximación racional similar en amplitud. Sin embargo, su teorema no tuvo en cuenta el hecho de que las fracciones equivalentes deberían contarse solo una vez.


Dimitris Cuculopoulos (izquierda) y James Maynard en la presentación de su evidencia en una conferencia en Italia

"Típicamente, las matemáticas para el primer grado no deberían afectar la resolución de problemas", dijo Granville. "Pero en este caso, sorprendentemente, ella influyó".

Por lo tanto, la hipótesis de Duffin-Shaffer tiene un término que cuenta el número de fracciones únicas (o fracciones reducidas) para cada denominador. Este miembro se llama la función φ de Euler en honor de su inventor, el matemático del siglo XVIII, Leonard Euler. φ (10) es 4, porque entre 0 y 1 solo hay cuatro fracciones reducidas con un denominador de 10: 1/10, 3/10, 7/10 y 9/10.

El siguiente paso es calcular cuántos números irracionales se pueden aproximar usando cada una de las fracciones dadas. Depende del error de tamaño que esté dispuesto a aceptar. La hipótesis de Duffin-Shaffer nos permite elegir un error para cada uno de los denominadores. Por ejemplo, para fracciones con un denominador de 7, puede tomar un error permisible de 0.02. Para el denominador 10, puede tomar el error 0.01.

Una vez identificados los denominadores y los términos de los errores, es hora de poner las redes en números irracionales. Construya sus fracciones en una recta numérica entre 0 y 1, y dibuje errores en forma de redes que se extiendan desde la fracción a cada lado. Podemos decir que todos los números irracionales que entran en la red están "satisfactoriamente aproximados" para los términos dados. La pregunta es: ¿cuántos números irracionales has atrapado?



En cualquier intervalo de la recta numérica contiene un número infinito de números irracionales, por lo que no se puede escribir el número exacto de números irracionales capturados. En cambio, los matemáticos hablan sobre la proporción del número total de números irracionales capturados por cada fracción. Evalúan estas proporciones utilizando un concepto como la "medida" de un subconjunto de números: es algo así como estimar el número de peces capturados por peso en lugar de la cantidad.

La hipótesis de Duffin-Schaffer sugiere sumar todas las medidas de los subconjuntos de números irracionales capturados por cada una de las fracciones aproximadas. Ella representa este número como una gran suma aritmética. Luego hace su predicción principal: si esta suma llega al infinito, entonces aproximaste casi todos los números irracionales; si solo da el valor final, independientemente de cuántas medidas haya resumido, entonces no pudo aproximar casi ningún número irracional.

Una pregunta similar, si la suma "diverge" al infinito o "converge" a un valor finito, surge en muchas áreas de las matemáticas. La afirmación principal de la hipótesis de Duffin-Shaffer es que si desea comprender si puede aproximar casi todos los números irracionales utilizando un conjunto dado de denominadores y errores, entonces solo necesita saber una cosa: la suma infinita de medidas diverge al infinito, o converge al valor final

"Al final, no importa cómo decida evaluar la aproximación para cada denominador, su éxito depende completamente de una sola cosa: si la secuencia interminable diverge o no", dijo Waaler.

Toma de decisiones

Quizás se pregunte: ¿qué pasa si los números aproximados por una fracción se cruzan con los números aproximados por otra? ¿No los tendremos en cuenta dos veces al calcular las medidas?

Para algunas secuencias de aproximación, el doble conteo no importa. Los matemáticos hace varias décadas demostraron que esta hipótesis es válida para las secuencias de aproximación que consisten en números primos. Pero para muchas otras secuencias de aproximación, el doble conteo es un problema. Por lo tanto, los matemáticos no pudieron abordar esta hipótesis durante 80 años.

El grado en que diferentes denominadores capturan conjuntos de números irracionales que se cruzan se refleja en el número de divisores simples comunes a todos los denominadores. Considere los números 12 y 35. Los divisores primos de 12 son 2 y 3. Los divisores primos de 35 son 5 y 7. En otras palabras, los factores primos comunes de 12 y 35 no lo hacen, como resultado, hay muchos números irracionales que pueden aproximarse por fracciones de Los denominadores 12 y 35 no se cruzan particularmente.

¿Qué pasa con los denominadores 12 y 20? En 20, los divisores simples son 2 y 5 que se cruzan con los divisores 12. De la misma manera, los números irracionales que se pueden aproximar por fracciones con un denominador de 20 se cruzan con los que se pueden aproximar por fracciones con un denominador de 12. La hipótesis de Duffin-Shaffer es la más difícil de demostrar en tales situaciones, cuando los números en la secuencia de aproximación tienen muchos divisores primos pequeños comunes, y se produce la intersección de muchos subconjuntos de números que cada uno de los denominadores se aproxima.

"Cuando muchos de los denominadores de los que eliges tienen muchos divisores simples pequeños, comienzan a interferir entre sí", dijo Sam Chau de Oxford.

La clave para resolver la hipótesis fue encontrar una manera de calcular con precisión las superposiciones mutuas de subconjuntos de números irracionales, que se aproximan por denominadores que tienen divisores primos comunes. Durante 80 años, nadie ha logrado hacer esto. Cuculopoulos y Maynard tuvieron éxito, encontrando un punto de vista completamente nuevo sobre el problema.


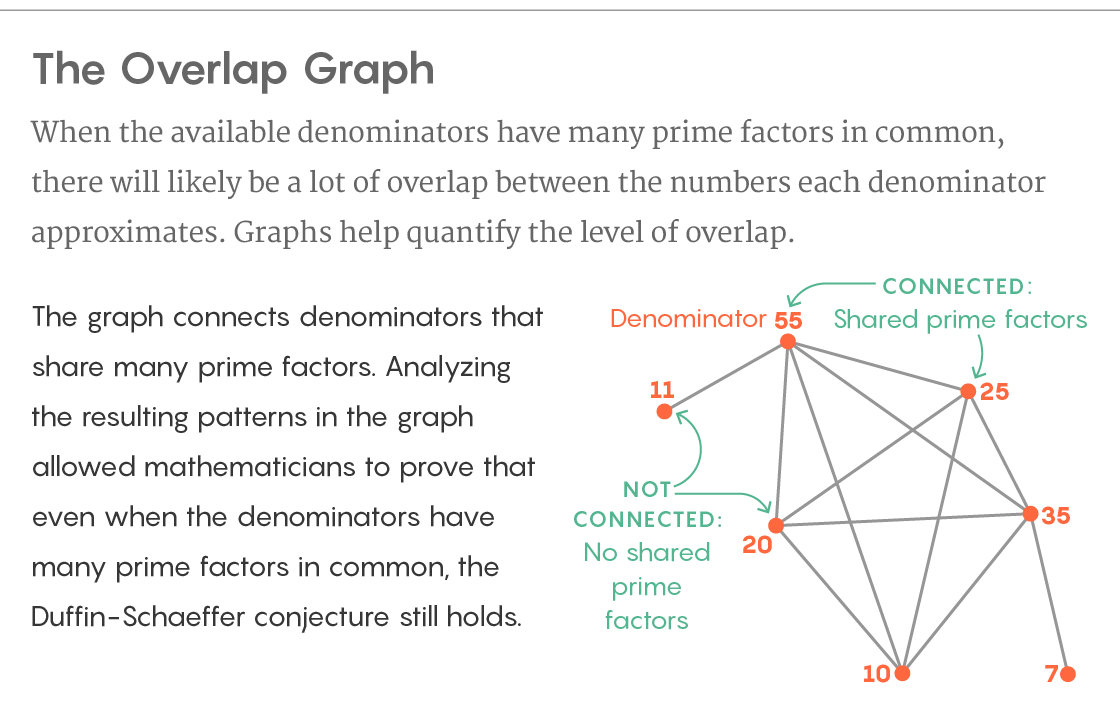Recuento de superposición mutua

En su nueva prueba, construyen una gráfica a partir de sus denominadores. Los construyen como vértices del gráfico y conectan los vértices con un borde si tienen muchos divisores primos comunes. La estructura del gráfico describe la superposición de los subconjuntos de números irracionales que cada uno de los denominadores aproxima. Y aunque esta superposición es difícil de investigar directamente, Cuculopoulos y Maynard encontraron una manera de analizar la estructura del gráfico utilizando herramientas de la teoría de gráficos, y la información que necesitaban se encontró de esta manera.

"El gráfico ayuda a comprender visualmente la tarea, es un lenguaje hermoso en el que puedes reflexionar sobre el problema", dijo Kukulopulos.

Cuculopoulos y Maynard demostraron que la hipótesis de Duffin-Shaffer es cierta: si se le proporcionó una lista de denominadores con errores válidos, puede determinar si es posible aproximar casi todos los números irracionales, o no se puede hacer simplemente comprobando si la suma de medidas correspondiente diverge al infinito o converge a un valor finito.

Esta es una prueba elegante, que toma la amplia pregunta de la naturaleza de la aproximación por números racionales y la reduce a un solo valor calculado. Tras demostrar la universalidad de las pruebas, Cuculopoulos y Maynard hicieron una de las mejores cosas para las matemáticas: dieron la respuesta final a una pregunta fundamental en su campo.

"Su prueba se ha convertido en un resultado necesario y suficiente", dijo Green. "Supongo que marca el final del próximo capítulo en matemáticas".