La agrupación en clúster es una parte importante del proceso de aprendizaje automático para resolver problemas científicos y empresariales. Ayuda a identificar conjuntos de puntos estrechamente relacionados (una cierta medida de distancia) en la nube de datos que podrían ser difíciles de determinar por otros medios.

Sin embargo, el proceso de agrupamiento en su mayor parte se relaciona con el campo del aprendizaje automático sin un maestro , que se caracteriza por una serie de dificultades. No hay respuestas o consejos sobre cómo optimizar el proceso o evaluar el éxito de la capacitación. Este es un territorio desconocido.

Por lo tanto, no es sorprendente que el método popular de agrupamiento por el método k-promedio no responda completamente a nuestra pregunta: "¿Cómo descubrimos primero el número de grupos?" Esta pregunta es extremadamente importante, porque la agrupación a menudo precede al procesamiento posterior de grupos individuales, y la cantidad de recursos informáticos puede depender de la evaluación de su número.

Las peores consecuencias pueden surgir en el campo del análisis empresarial. Aquí, la agrupación se utiliza para la segmentación del mercado, y es posible que el personal de marketing se asigne de acuerdo con el número de agrupaciones. Por lo tanto, una estimación errónea de esta cantidad puede conducir a una asignación no óptima de recursos valiosos.

Método del codo

Cuando se agrupa con el método k-means, el número de grupos se estima con mayor frecuencia utilizando el "método del codo" . Implica la ejecución cíclica múltiple del algoritmo con un aumento en el número de grupos seleccionables, así como el aplazamiento posterior del puntaje de agrupamiento en el gráfico, calculado en función del número de grupos.

¿Cuál es esta puntuación, o métrica, que se retrasa en el gráfico? ¿Por qué se llama el método del codo ?

Un gráfico típico se ve así:



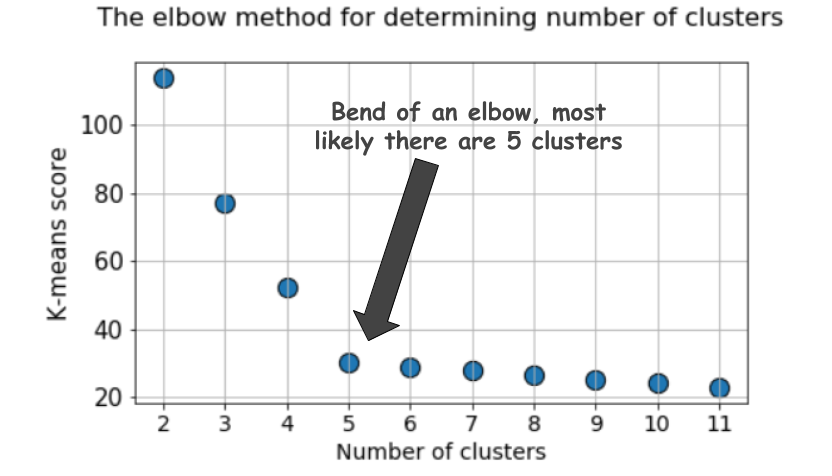
El puntaje, como regla, es una medida de los datos de entrada para la función objetivo de k-medias, es decir, alguna forma de la relación entre la distancia intragrupo y la distancia entre grupos.

Por ejemplo, este método de puntuación está disponible de inmediato en la herramienta de puntuación k-means en Scikit-learn.

Pero eche otro vistazo a este gráfico. Se siente algo extraño. ¿Cuál es el número óptimo de grupos que tenemos, 4, 5 o 6?

No está claro, ¿verdad?

La silueta es una mejor métrica

El coeficiente de silueta se calcula utilizando la distancia promedio dentro del clúster (a) y la distancia promedio al grupo más cercano (b) para cada muestra. La silueta se calcula como (b - a) / max(a, b) . Permítanme explicar: b es la distancia entre b el grupo más cercano al que a no pertenece. Puede calcular el valor de silueta promedio para todas las muestras y usarlo como una métrica para estimar el número de grupos.

Aquí hay un video que explica esta idea:


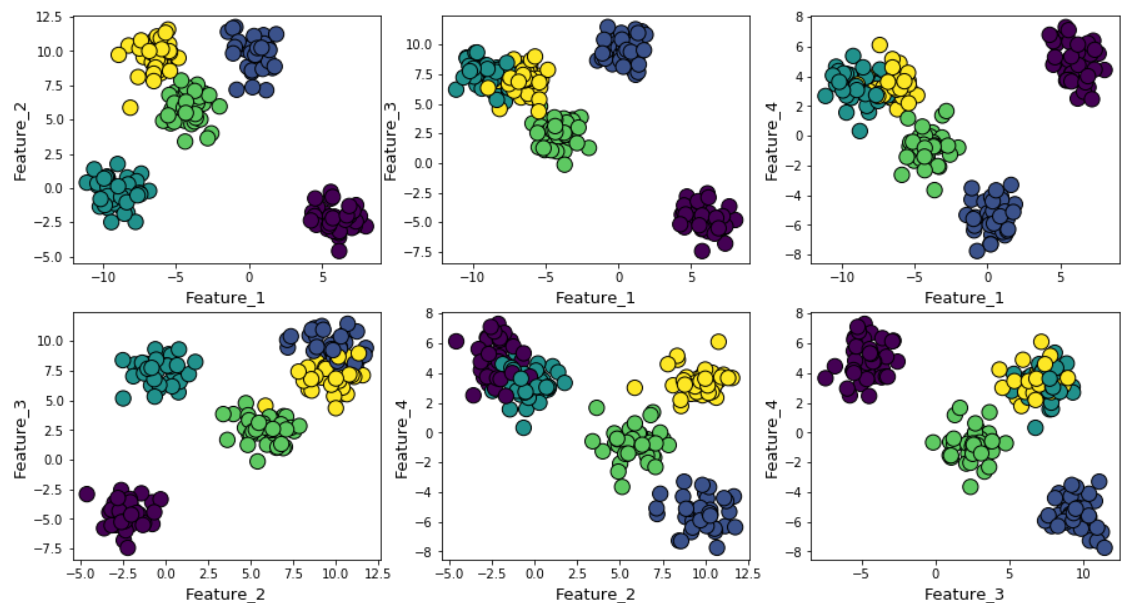
Supongamos que generamos datos aleatorios usando la función make_blob de Scikit-learn. Los datos se encuentran en cuatro dimensiones y alrededor de cinco centros de clúster. La esencia del problema es que los datos se generan alrededor de cinco centros de clúster. Sin embargo, el algoritmo k-means no sabe sobre esto.

Los grupos se pueden mostrar en el gráfico de la siguiente manera (signos por pares):



Luego ejecutamos el algoritmo de k-medias con valores de k = 2 a k = 12, y luego calculamos la métrica predeterminada para k-medias y el valor de silueta promedio para cada carrera, con los resultados mostrados en dos gráficos adyacentes.



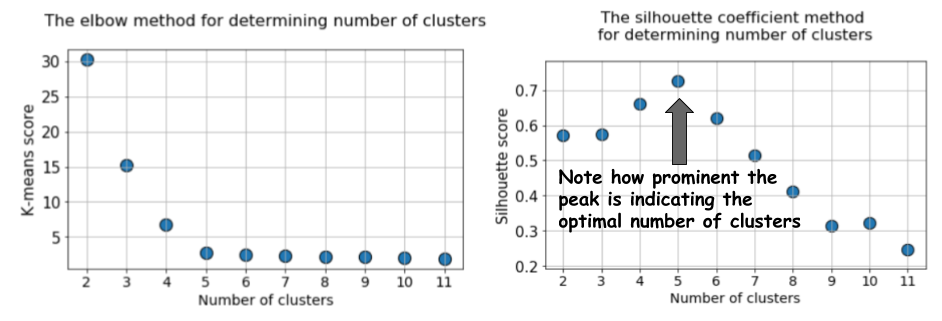
La diferencia es obvia. El valor promedio de la silueta aumenta a k = 5, y luego disminuye bruscamente para valores más altos de k . Es decir, obtenemos un pico pronunciado en k = 5, este es el número de grupos generados en el conjunto de datos original.

El gráfico de silueta tiene un carácter de pico, en contraste con el gráfico suavemente curvado cuando se utiliza el método del codo. Es más fácil de visualizar y justificar.

Si aumenta el ruido gaussiano durante la generación de datos, los grupos se superpondrán más fuertemente.



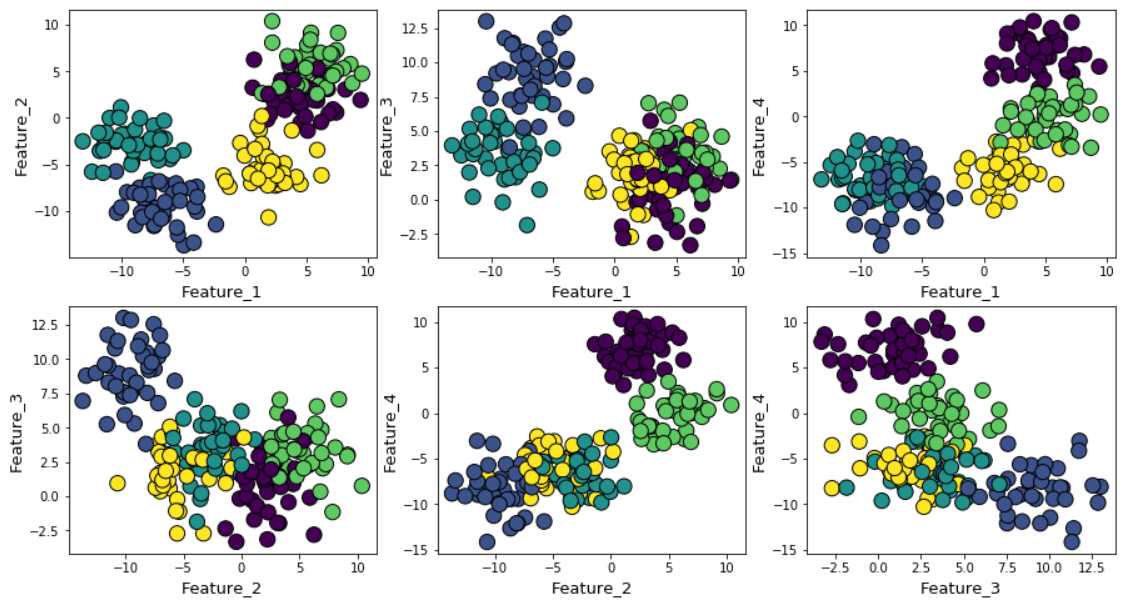
En este caso, calcular las medias k predeterminadas utilizando el método del codo da un resultado aún más incierto. A continuación se muestra un gráfico del método del codo, en el que es difícil elegir un punto adecuado en el que la línea se doble realmente. ¿Es 4, 5, 6 o 7?



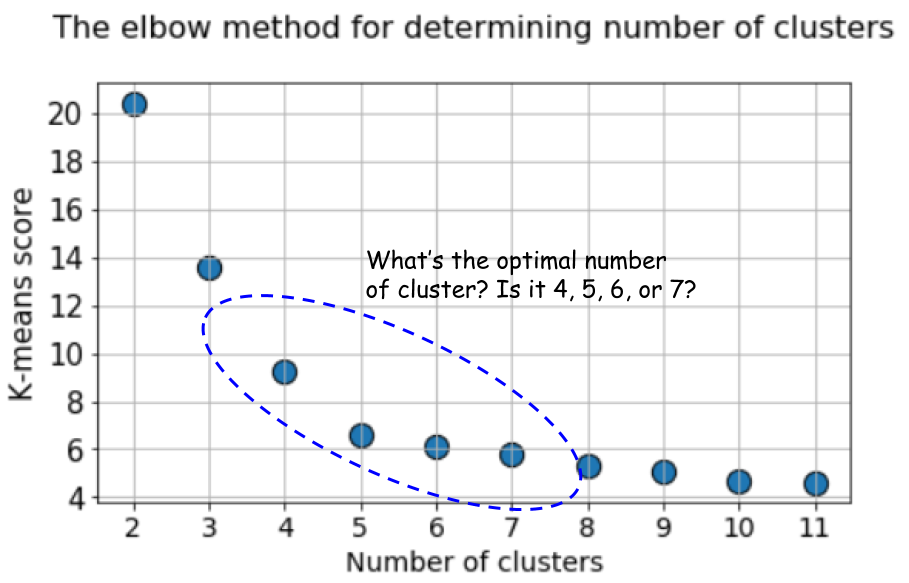
Al mismo tiempo, el gráfico de silueta todavía muestra un pico en la región de 4 o 5 centros de agrupación, lo que facilita enormemente nuestras vidas.

Si observa que los clústeres se superponen entre sí, verá que, a pesar del hecho de que generamos datos alrededor de 5 centros, debido a la alta dispersión, solo se pueden distinguir estructuralmente 4 grupos. La silueta revela fácilmente este comportamiento y muestra el número óptimo de grupos entre 4 y 5.

Puntaje BIC con modelo de mezcla de distribución normal

Existen otras excelentes métricas para determinar la verdadera cantidad de clústeres, como el Criterio de información bayesiano (BIC). Pero solo se pueden aplicar si necesitamos cambiar del método k-means a una versión más generalizada, una mezcla de distribuciones normales (Modelo de mezcla gaussiana (GMM)).

GMM ve la nube de datos como una superposición de numerosos conjuntos de datos con una distribución normal, con valores medios y variaciones por separado. Y luego GMM usa un algoritmo para maximizar las expectativas para determinar estos promedios y variaciones.

BIC para regularización

Es posible que ya haya encontrado BIC en el análisis estadístico o al usar la regresión lineal. BIC y AIC (Criterio de información de Akaike, criterio de información de Akaike) se utilizan en regresión lineal como técnicas de regularización para el proceso de selección de variables.

Una idea similar se aplica a BIC. Teóricamente, los grupos extremadamente complejos se pueden modelar como superposiciones de una gran cantidad de conjuntos de datos con una distribución normal. Para resolver este problema, puede aplicar un número ilimitado de tales distribuciones.
Pero esto es similar a aumentar la complejidad del modelo en regresión lineal, cuando se puede usar una gran cantidad de propiedades para unir datos de cualquier complejidad, solo para perder la posibilidad de generalización, ya que un modelo demasiado complejo corresponde al ruido y no a un patrón real.

El método BIC multa numerosas distribuciones normales e intenta mantener el modelo lo suficientemente simple como para describir un patrón dado.

Por lo tanto, puede ejecutar el algoritmo GMM para una gran cantidad de centros de clúster, y el valor BIC aumentará hasta cierto punto y luego comenzará a disminuir a medida que crezca la multa.

Resumen

Aquí está el cuaderno Jupyter para este artículo. Siéntase libre de bifurcar y experimentar.

Nosotros en Jet Infosystems discutimos un par de alternativas al popular método del codo en términos de elegir el número correcto de grupos cuando se aprende sin un maestro usando el algoritmo k-means.

Nos aseguramos de que en lugar del método del codo, es mejor usar el coeficiente de "silueta" y el valor BIC (de la extensión GMM para k-medias) para determinar visualmente el número óptimo de grupos.