Hola

Aquí describimos el trabajo de cierto campo y luego hacemos un par de características hermosas (todo es MUY simple aquí).

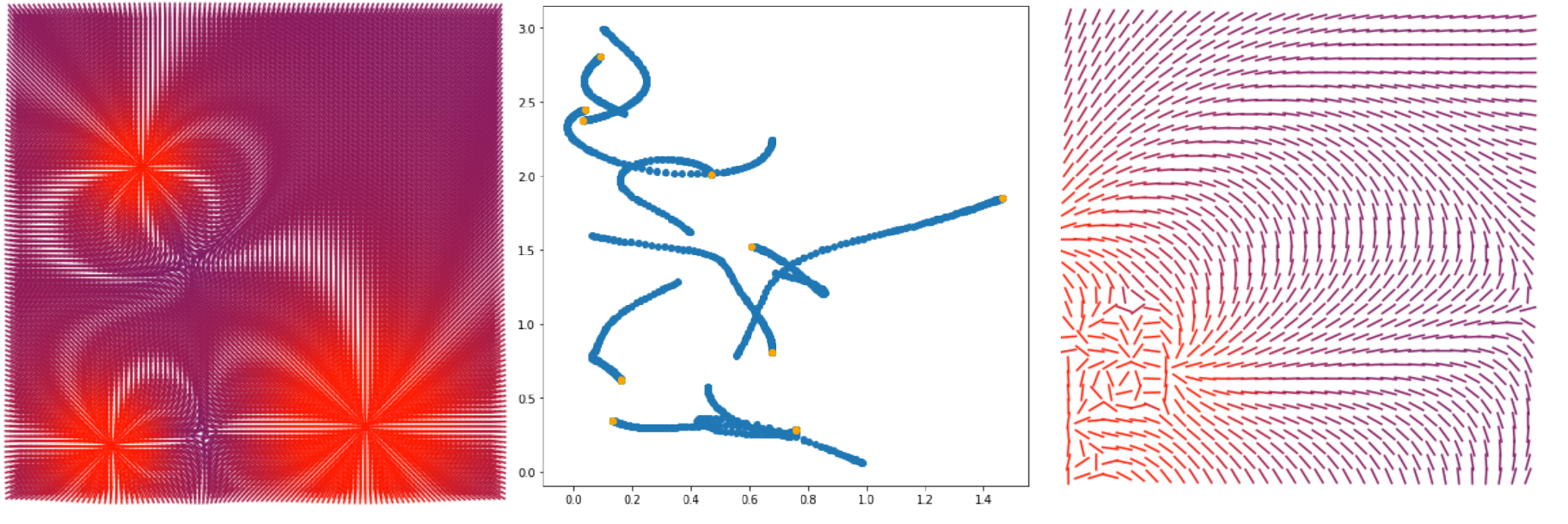
Lo que sucederá en este artículo.

Caso general:

Describimos la base, a saber, trabajar con vectores (una bicicleta para aquellos que no tienen numpy a mano)
Describimos el punto material y el campo de interacción.

Caso especial (basado en general):

Hagamos una visualización del campo vectorial de la intensidad del campo electromagnético (primera y tercera imagen)
Visualizaremos el movimiento de partículas en un campo electromagnético.

Nos vemos bajo el corte!

Programación teórica de fondo

Vector

La base de todos los fundamentos es un vector (especialmente en nuestro caso). Por lo tanto, es con la descripción del vector que comenzaremos. Que necesitamos Operaciones aritméticas en un vector, distancia, módulo y un par de cosas técnicas. El vector que heredaremos de la lista. Así es como se ve su inicialización:

class Vector(list): def __init__(self, *el): for e in el: self.append(e)

Es decir, ahora podemos crear un vector con

 v = Vector(1, 2, 3)

Establezcamos la operación aritmética además:

 class Vector(list): ... def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other

Genial:

 v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 + v2 >>> [3, 59, 26.2]

Definimos de manera similar todas las operaciones aritméticas (el código completo del vector será menor). Ahora necesitas la función de distancia. Podría hacer un dist rústico (v1, v2), pero esto no es hermoso, así que redefina el operador%:

 class Vector(list): ... def __mod__(self, other): return sum((self - other) ** 2) ** 0.5

Genial:

 v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 % v2 >>> 58.60068258988115

También necesitamos un par de métodos para una generación de vectores más rápida y una salida hermosa. Aquí no hay nada complicado, así que aquí está el código completo de la clase Vector:

Todos los códigos de clase de vectores

 class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)])

Punto material

Aquí, en teoría, todo es simple: el punto tiene coordenadas, velocidad y aceleración (por simplicidad). Además, ella tiene una masa y un conjunto de parámetros personalizados (por ejemplo, para un campo electromagnético, una carga no nos hace daño, pero nadie te molesta para establecer un giro).

La inicialización será la siguiente:

 class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop])

Y para mover, inmovilizar y acelerar nuestro punto, escribiremos los siguientes métodos:

 class Point: ... def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): #        self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0

Bien hecho, el punto en sí está hecho.

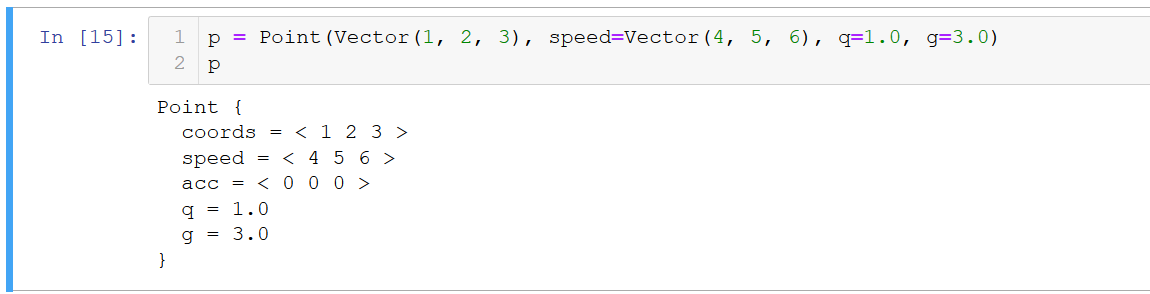
Código de punto (con buena salida)

 class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self))

Resultado:

Campo de interacción

Llamamos al campo de interacción un objeto que incluye el conjunto de todos los puntos materiales y ejerce fuerza sobre ellos. Consideraremos un caso especial de nuestro maravilloso universo, por lo que tendremos una interacción personalizada (por supuesto, esto es fácil de expandir). Declara un constructor y agrega un punto:

 class InteractionField: def __init__(self, F): # F -   , F(p1, p2, r), p1, p2 - , r -    self.points = [] self.F = F def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs))

Ahora la parte divertida es declarar una función que devuelve "tensión" en ese punto. Aunque este concepto se refiere a la interacción electromagnética, en nuestro caso es un vector abstracto a lo largo del cual moveremos el punto. En este caso, tendremos la propiedad del punto q, en el caso particular: la carga del punto (en general, lo que queramos, incluso el vector). Entonces, ¿qué es la tensión en el punto C? Algo como esto:

v e c E (v e c C) = s u m v e c F_{i} (v e c C)

$\ vec E (\ vec C) = \ sum {\ vec F_i (\ vec C)}$

Es decir, la tensión en el punto

v e c C

$\ vec C$ igual a la suma de las fuerzas de todos los puntos materiales que actúan sobre algún punto unitario.

 class InteractionField: ... def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) #       (   ,       F,      ) for p in self.points: if coord % p.coords < 10 ** (-10): #      ,        ,   ,     (  ) continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) #    -  proj = proj + (coord - p.coords) / d * fmod #  return proj

En este punto, ya puede dibujar un campo vectorial, pero lo haremos al final. Ahora demos un paso en nuestra interacción

 class InteractionField: ... def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt)

Todo es simple aquí. Para cada punto, determinamos la tensión en estas coordenadas y luego determinamos la fuerza final sobre el punto material de la ETU:

v e c F = v e c E * q

$\ vec F = \ vec E * q$

Definir las funciones que faltan.

Todo el código InteractionField

 class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points]

Un caso especial. Movimiento de partículas y visualización del campo vectorial.

Entonces llegamos a lo más interesante. Comencemos con ...

Modelado del movimiento de partículas en un campo electromagnético.

 u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)

De hecho, el coeficiente k debería ser igual a algún tipo de billones (9 * 10 ^ (- 9)), pero dado que se extinguirá cuando t -> 0, inmediatamente decidí convertirlos en números adecuados. Por lo tanto, en nuestra física k = 300'000. Y con todo lo demás, creo que está claro.

r ** 2 + 0.1

- esta es la forma de evitar dividir por 0. Nosotros, por supuesto, podríamos estar confundidos, resolver un gran sistema de difours, pero en primer lugar no existe una ecuación de movimiento para más de 2 cuerpos, y en segundo lugar esto claramente no está incluido en el concepto de "artículo para principiantes"

Luego, agregamos diez puntos (espacio bidimensional) con coordenadas de 0 a 10 a lo largo de cada eje. Además, le damos a cada punto un cargo de -0.25 a 0.25. Ahora haga un bucle y dibuje puntos de acuerdo con sus coordenadas (y trazas):

 X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show()

Lo que debería haber sucedido:

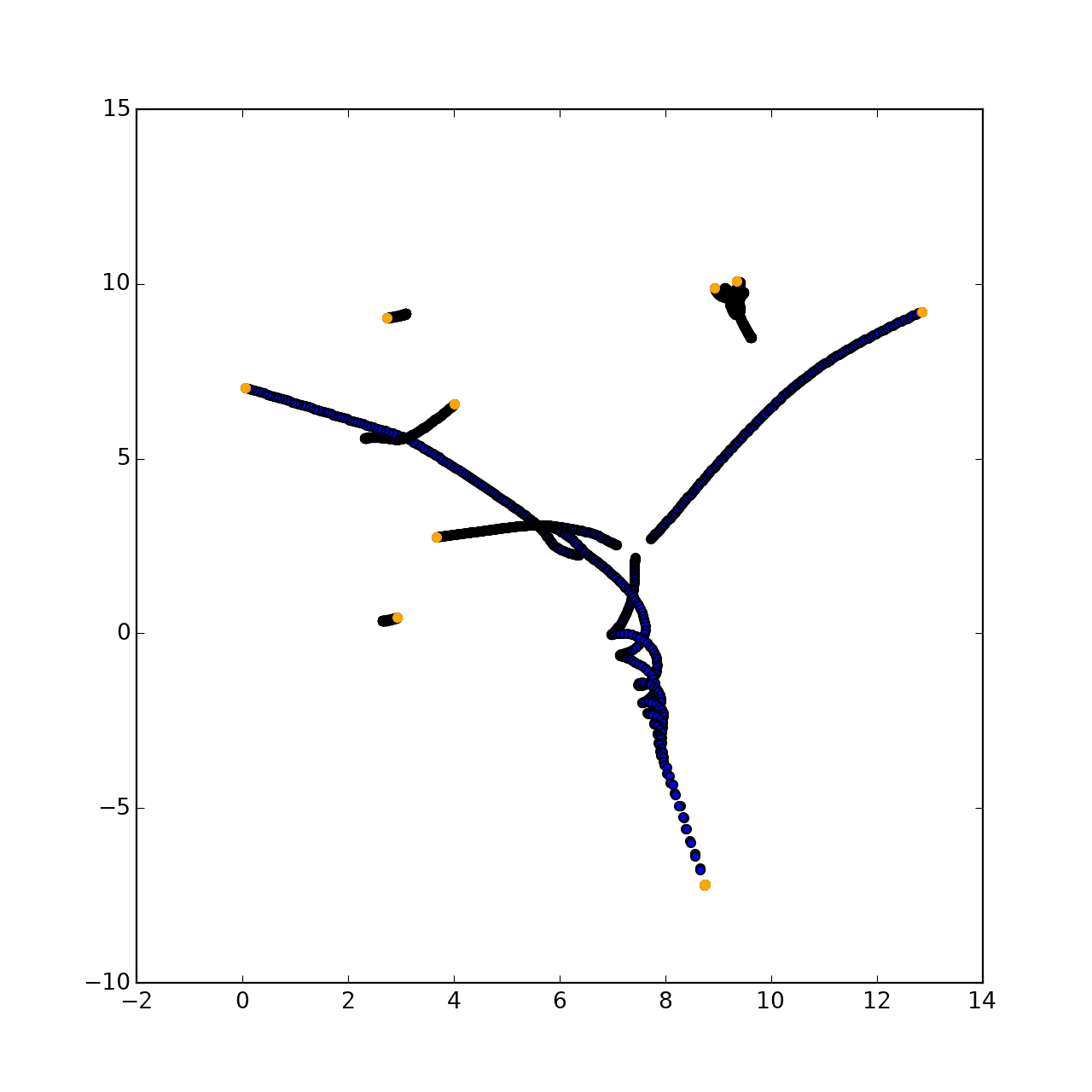
De hecho, el dibujo allí será completamente aleatorio, porque la trayectoria de cada punto es impredecible en el momento del desarrollo de la mecánica.

Visualización de campo vectorial

Todo es simple aquí. Necesitamos recorrer las coordenadas con algún paso y dibujar un vector en cada una de ellas en la dirección correcta.

 fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 4 #     res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F)) for r in res: plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) #        plt.show()

Aproximadamente esta conclusión debería haberse obtenido.

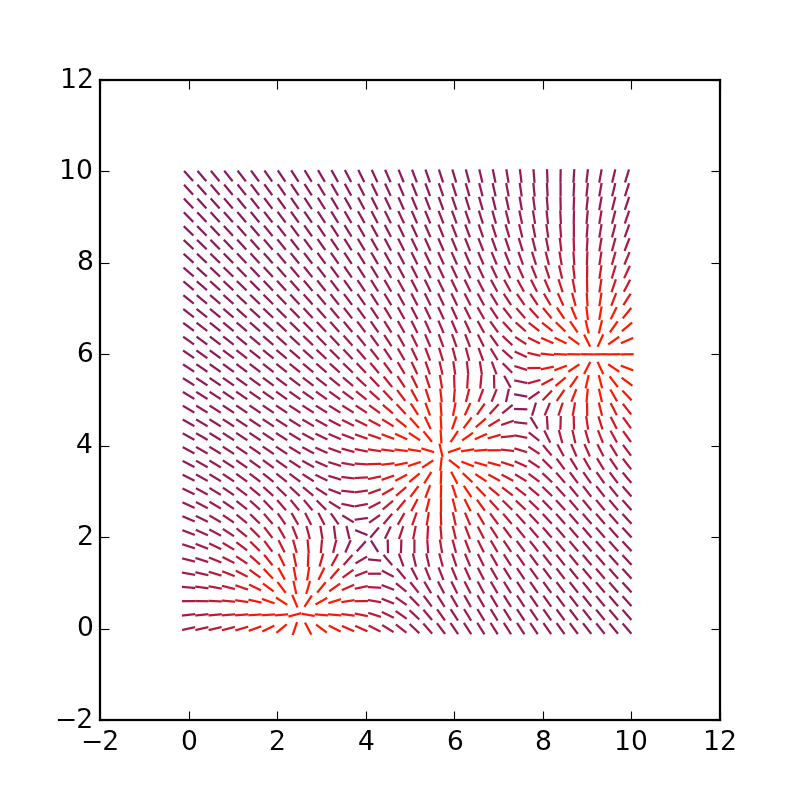
Puede alargar los propios vectores, reemplazar * 4 con * 1.5:

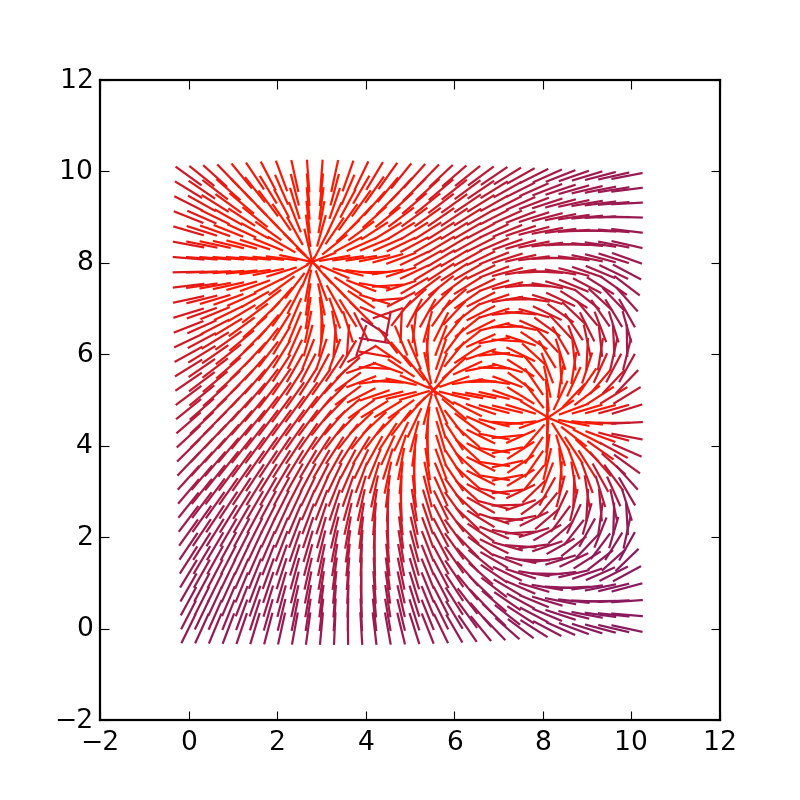
Jugamos con la dimensionalidad y el modelaje.

Cree un espacio de cinco dimensiones con 200 puntos y una interacción que no dependa del cuadrado de la distancia, sino del cuarto grado.

 u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)

Ahora todas las coordenadas, velocidades, etc. están definidas en cinco dimensiones. Ahora modelemos algo:

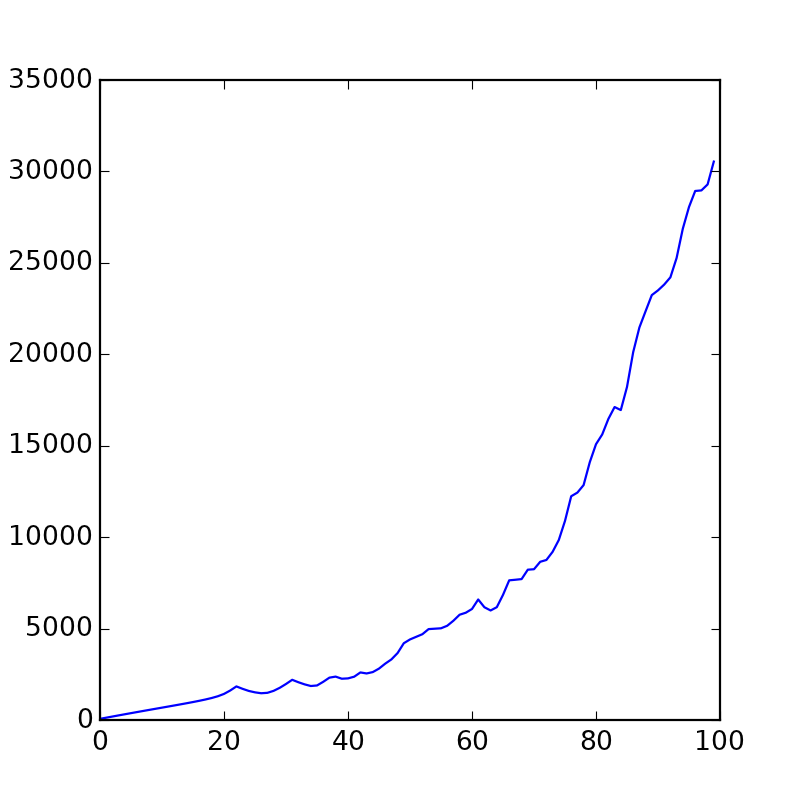
 velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points]) #       velocities.append(velmod) plt.plot(velocities) plt.show()

Este es un gráfico de la suma de todas las velocidades en un momento dado. Como puede ver, con el tiempo se aceleran lentamente.

Bueno, esa fue una breve instrucción sobre cómo hacer algo tan simple. Pero qué pasa si juegas con flores:

Todo el código con demo

 import random class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)]) class Point: def __init__(self, coords, mass=1.0, q=1.0, speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self)) class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points] #  import matplotlib.pyplot as plt import numpy as np import time #     if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(10): u.append(Vector.randvec(2) * 10, q=(random.random() - 0.5) / 2) X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show() def sigm(x): return 1 / (1 + 1.10 ** (-x/1000)) #    if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5) fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 1.5 res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F)) for r in res: plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) plt.show() #    5-  if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5) velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points]) velocities.append(velmod) plt.plot(velocities) plt.show()

El próximo artículo probablemente será sobre modelos más complejos, y tal vez los fluidos y las ecuaciones de Navier-Stokes.
UPD: un artículo escrito por mi colega aquí

Gracias a MomoDev por ayudar a renderizar el video.

Simulación elemental de interacción física personalizada en python + matplotlib