Y, sin embargo, por qué Posit es una alternativa digna a IEEE 754

El Mes de Posit sobre Habré ha sido declarado abierto, lo que significa que no puedo pasar por alto e ignorar las críticas que han caído sobre ellos. En series anteriores:

Un nuevo enfoque puede ayudarnos a deshacernos de los cálculos de coma flotante
Posit-aritmética: derrotando un punto flotante en su propio campo. Parte 1
Posit-aritmética: derrotando un punto flotante en su propio campo. Parte 2
Desafíos de posición adulta

Creo que muchos de ustedes pueden recordar inmediatamente al menos un caso de la historia cuando las ideas revolucionarias en el momento de su formación se vieron rechazadas por una comunidad de expertos. Como regla general, la culpa de tal comportamiento es el gran bagaje de conocimiento ya acumulado que no permite mirar el viejo problema bajo una nueva luz. Por lo tanto, la nueva idea pierde en términos de características a los enfoques establecidos, porque se evalúa solo por aquellas métricas que se consideraron importantes en la etapa anterior de desarrollo.

Este es precisamente el tipo de aversión que enfrenta el formato Posit hoy en día: los críticos a menudo simplemente "miran en la dirección equivocada" e incluso usan el Posit en sus experimentos de la manera incorrecta. En este artículo intentaré explicar por qué.

Las ventajas de Posit ya se mencionaron bastante: elegancia matemática, alta precisión en valores con un exponente bajo, una amplia gama de valores, solo una representación binaria de NaN y cero, la ausencia de valores subnormales, la lucha contra el desbordamiento / desbordamiento. Las críticas se han expresado bastante: precisión inútil para valores muy grandes o muy pequeños, un formato de representación binario complejo y, por supuesto, falta de soporte de hardware.

No quiero repetir los argumentos que ya he dicho; en cambio, trataré de centrarme en el aspecto que, por regla general, se pasa por alto.

Las reglas del juego han cambiado

El estándar IEEE 754 describe los números de coma flotante implementados en el Intel 8087 hace casi 40 años. Según los estándares de nuestra industria, este es un momento increíble; todo ha cambiado desde entonces: rendimiento del procesador, costo de memoria, volúmenes de datos y escala de cálculos. El formato Posit se desarrolló no solo como la mejor versión de IEEE 754, sino como un enfoque para trabajar con números que cumple con los nuevos requisitos de la época.

La tarea de alto nivel se ha mantenido igual: todos necesitamos cálculos efectivos sobre el campo de los números racionales con una pérdida mínima de precisión. Pero las condiciones bajo las cuales se resuelve la tarea cambian radicalmente.

Primero, las prioridades para la optimización han cambiado. Hace 40 años, el rendimiento de la computadora dependía casi por completo del rendimiento del procesador. Hoy, el rendimiento de la mayoría de la informática descansa en la memoria. Para verificar esto, solo observe las áreas clave de desarrollo de procesadores de las últimas décadas: almacenamiento en caché de tres niveles, ejecución especulativa, canalización de cálculos, predicción de ramificaciones. Todos estos enfoques están destinados a lograr un alto rendimiento en las condiciones de computación rápida y acceso lento a la memoria.



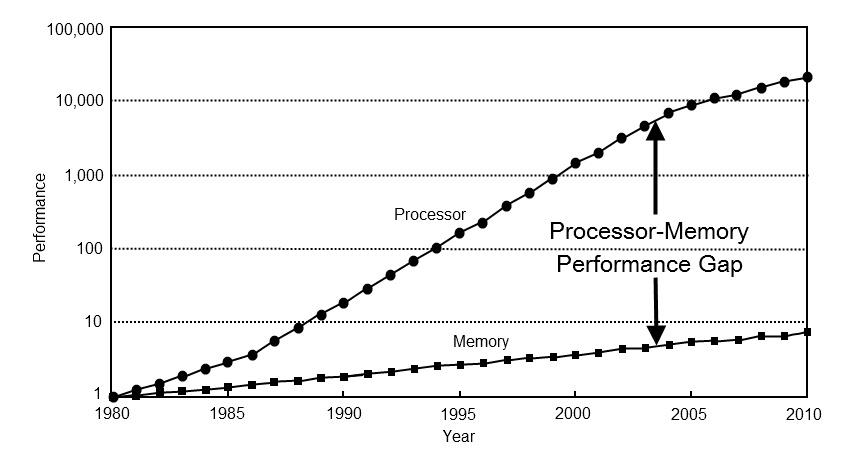
En segundo lugar, ha surgido un nuevo requisito: el consumo efectivo de energía. En las últimas décadas, la tecnología de escala horizontal de la informática ha avanzado tanto que comenzamos a preocuparnos no tanto por la velocidad de estos cálculos, sino por la factura de la electricidad. Aquí debo enfatizar una parte importante para entender. Desde el punto de vista de la eficiencia energética, los cálculos son baratos, porque los registros del procesador están muy cerca de sus computadoras. Será mucho más costoso pagar la transferencia de datos, tanto entre el procesador y la memoria (x100), como a largas distancias (x1000 ...).



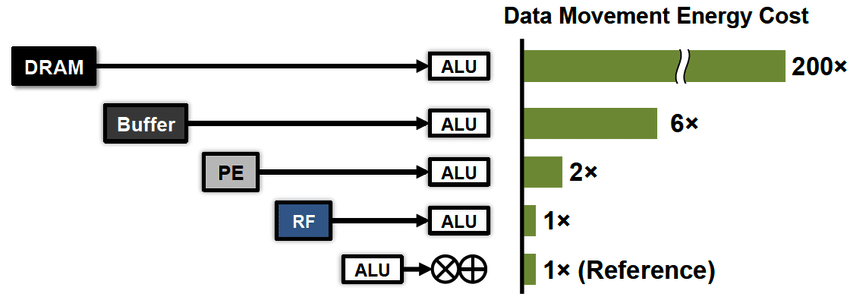
Aquí hay solo un ejemplo de un proyecto científico que Posit planea usar:



Esta red de telescopios genera 200 petabytes de datos por segundo, cuyo procesamiento toma el poder de una pequeña planta de energía: 10 megavatios . Obviamente, para tales proyectos, la reducción de datos y consumo de energía es crítica.

Hasta el principio

Entonces, ¿qué ofrece el estándar Posit? Para comprender esto, debe volver al comienzo de la discusión y comprender qué se entiende por la precisión de los números de coma flotante.

En realidad, hay dos aspectos diferentes relacionados con la precisión. El primer aspecto es la precisión de los cálculos : cuánto se desvían los resultados de los cálculos durante varias operaciones. El segundo aspecto es la precisión de la presentación : cuánto se distorsiona el valor original en el momento de la conversión del campo de números racionales al campo de números de coma flotante de un formato particular.

Ahora habrá un momento importante para la conciencia. Posit es principalmente un formato para representar números racionales, no una forma de realizar operaciones en ellos. En otras palabras, Posit es un formato de compresión racional con pérdida. Es posible que haya escuchado la afirmación de que Posit de 32 bits es una buena alternativa a Float de 64 bits. Entonces, estamos hablando de reducir a la mitad con precisión la cantidad requerida de datos para almacenar y transmitir el mismo conjunto de números. Dos veces menos memoria: casi 2 veces menos consumo de energía y alto rendimiento del procesador debido a las menores expectativas de acceso a la memoria.

Segundo extremo del palo

Aquí debe tener una pregunta lógica: ¿cuál es el punto de representar eficientemente números racionales si no permite que los cálculos se realicen con alta precisión?

De hecho, hay una manera de hacer cálculos exactos, y se llama Quire. Este es otro formato para representar números racionales, inextricablemente vinculados con Posit. A diferencia de Posit, el formato Quire está diseñado específicamente para cálculos y para almacenar valores intermedios en registros, y no en la memoria principal.



En resumen, el Quire no es más que una batería entera ancha (aritmética de punto fijo). La unidad, como representación binaria de Quire, corresponde al valor positivo mínimo de Posit. El valor máximo de Quire corresponde al valor máximo de Posit. Cada valor Posit tiene una representación única en Quire sin pérdida de precisión, pero no todos los valores de Quire pueden representarse en Posit sin pérdida de precisión.

Los beneficios de Quire son obvios. Le permiten realizar operaciones con una precisión incomparablemente más alta que Float, y para las operaciones de suma y multiplicación no habrá pérdida de precisión en absoluto. El precio que debe pagar por esto son registros de procesador amplios (la posición de 32 bits con es = 2 corresponde a Quire de 512 bits), pero esto no es un problema grave para los procesadores modernos. Y si hace 40 años la computación de enteros de más de 512 bits parecía un lujo inaceptable, hoy es más bien una alternativa adecuada al amplio acceso a la memoria.

Armar el rompecabezas

Por lo tanto, Posit ofrece no solo un nuevo estándar en forma de una alternativa a Float / Double, sino más bien un nuevo enfoque para trabajar con números. A diferencia de Float, que es una representación única que trata de encontrar un compromiso entre la precisión y la eficiencia del almacenamiento y la eficiencia computacional, Posit ofrece dos formatos de presentación diferentes, uno para almacenar y transmitir números: Posit y el otro para los cálculos y sus intermedios. Valores - Quire.

Cuando resolvemos problemas prácticos utilizando números de coma flotante, desde el punto de vista del procesador, trabajar con ellos se puede representar como un conjunto de las siguientes acciones:

1. Leer los valores de los números de la memoria.
2. Realizar alguna secuencia de operaciones. A veces el número de operaciones es bastante grande. En este caso, todos los valores intermedios de los cálculos se almacenan en registros.
3. Escribe el resultado de las operaciones en la memoria.

Con Float / Double, se pierde precisión en cada operación. Con Posit + Quire, la pérdida de precisión durante el cálculo es insignificante. Se pierde solo en la última etapa, al momento de convertir el valor de Quire a Posit. Es por eso que la mayoría de los problemas de "acumulación de errores" para Posit + Quire simplemente no son relevantes.

A diferencia de Float / Double, cuando usamos Posit + Quire, generalmente podemos permitirnos una representación más compacta de los números. Como resultado, un acceso más rápido a los datos desde la memoria (mejor rendimiento) y un almacenamiento y transmisión de información más eficientes.

Ratio de Mueller

Como demostración visual, daré solo un ejemplo: la clásica relación de recurrencia de Muller, inventada específicamente para demostrar cómo la acumulación de errores en los cálculos de coma flotante distorsiona radicalmente el resultado de los cálculos.



En el caso de utilizar la aritmética con precisión arbitraria, la secuencia de recurrencia debe reducirse al valor de 5. En el caso de la aritmética de coma flotante, la pregunta es solo en qué iteración los resultados del cálculo comenzarán a tener una desviación inadecuadamente grande.

Realicé un experimento para IEEE 754 con precisión simple y doble, así como para Posit + Quire de 32 bits. Los cálculos se realizaron en aritmética Quire, pero cada valor de la tabla se convirtió en Posit.


Como puede ver en la tabla, Float de 32 bits ya se entrega en el séptimo valor, y Float de 64 bits duró hasta la decimocuarta iteración. Al mismo tiempo, los cálculos para Posit usando Quire devuelven un resultado estable de hasta 58 iteraciones.

Moraleja

Para muchos casos prácticos y cuando se usa correctamente, el formato Posit realmente le permitirá ahorrar en memoria, por un lado, comprimiendo los números mejor que Float y, por otro lado, proporcionará una mejor precisión de cálculo gracias a Quire.

¡Pero esto es solo una teoría! Cuando se trata de precisión o rendimiento, siempre realice pruebas antes de confiar ciegamente en un enfoque u otro. De hecho, en la práctica, su caso particular resultará excepcional con mucha más frecuencia que en teoría.

Bueno, no olvide la primera ley de Clark (interpretación libre): cuando un experto respetado y experimentado afirma que una nueva idea funcionará, es casi seguro que tiene razón. Cuando afirma que la nueva idea no funcionará, es muy probable que se equivoque. No me considero un experto experimentado para permitirle confiar en mi opinión, pero le pido que tenga cuidado de criticar incluso a las personas experimentadas y respetadas. Después de todo, el diablo está en los detalles, e incluso las personas experimentadas pueden extrañarlos.