Cantidad de problema

En la famosa tarea con monedas, que necesitan contar el cambio, como saben, hay dos problemas .
- el primero es el número de denominaciones de monedas,
- el segundo es el número de dígitos que representan el cambio.
Y ambas cantidades tienen un efecto exponencial en la carga de la máquina Turing, que en realidad está involucrada en el cálculo.
Reconocer que una persona tiene dos dependencias a la vez no se acepta ni siquiera en la sociedad de alcohólicos. Por lo tanto, decidí ir a lo seguro y deshacerme de uno de estos problemas de antemano. La forma en que será el número de denominaciones de monedas.

En pocas palabras, la esencia del problema se describe de la siguiente manera: dependencia exponencial. Es decir, el lanzamiento de un nuevo tipo de monedas de una denominación inexistente implica un doble aumento en el número de combinaciones de monedas. Otra denominación: el doble, y así hasta el infinito condicional. Con la inflación galopante, cuando se emiten nuevas monedas / billetes con la frecuencia suficiente, tendrá que comprar una computadora más potente para resolver el problema. ¿Y dónde obtener el dinero en una inflación galopante?

Entonces, una solución que en realidad es bastante simple.
Si imagina un segmento de cero a C (cambio) con los puntos correspondientes a las denominaciones de monedas, cualquier persona inteligente verá aproximadamente la siguiente imagen:

Bueno, tal vez en diferentes colores.
Entonces, ¿qué podemos decir sobre los puntos rojos? Por supuesto, el hecho de que el número correspondiente a cualquiera de estos puntos es la cantidad que podemos dar en forma de cambio. Y con una moneda. Quizás alguien vio algo más, pero yo, como artista, invertí precisamente este significado. Y, como artista, dibujaré otro punto en esta imagen que corresponde a la suma del primer punto (de izquierda a derecha) con el mismo punto (todo es correcto: duplicará el valor nominal). Dibujo en el mismo color, porque un nuevo punto significa lo mismo: esta cantidad también puede ser un cambio.

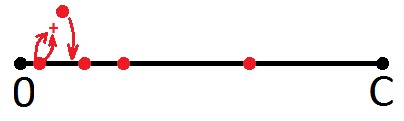
Luego, tomo el primer punto y resumo con el segundo, incluso si el segundo punto es la cantidad anterior (esto no importa, porque todos los puntos son iguales aquí). Voy a poner un nuevo punto en el segmento nuevamente.

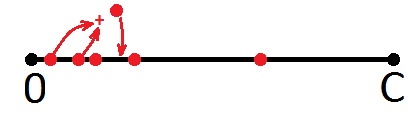
Si el nuevo punto va más allá de los límites del segmento, entonces no dibujamos nada, sino que volvemos al comienzo del segmento y tomamos el siguiente punto, es decir, el segundo. Más adelante lo mismo (de izquierda a derecha).
En realidad, cuando el punto C (les recuerdo, esto es cambio) se vuelve rojo, podemos suponer que se ha encontrado una solución. Y puede pasar por el ciclo completo y encontrar la solución óptima, de modo que el número de monedas sea mínimo.

Desde el punto de vista de la programación, hay dos ciclos. El primero es de 0 a C / 2 (no es necesario tomar el primer punto de mayor C / 2, ya que el segundo punto siempre es más grande que el primero y en total irán más allá de los límites del segmento). El segundo ciclo está integrado en el primero, comienza desde el mismo punto al que apunta el ciclo externo y hasta que la suma abandona los límites del segmento.
De hecho, esto es un fracaso: no perdemos una sola opción, y tenemos la garantía de encontrar la solución óptima, o concluiremos que no hay solución.

Vamos a contar la cantidad de iteraciones dentro de nuestros bucles. En el ciclo externo es C / 2, en el interno es casi lo mismo. Multiplicar C / 2 * C / 2 = (C ^ 2) / 4. Redondear a C al cuadrado. Esta es la peor opción cuando todo nuestro segmento consiste simplemente en puntos rojos. Si hay espacios entre los puntos, el número de iteraciones disminuirá significativamente.
Como puede ver, al determinar la dificultad de resolver el problema, no utilizamos el número de denominaciones de monedas. Este valor no afecta directamente la complejidad de la solución. Los valores de estas denominaciones afectan, digamos una moneda de 1 centavo y hacen que este segmento sea completamente rojo. Por lo tanto, es mejor no tener en cuenta esta moneda y, al final de la decisión, tomar el punto rojo más cercano a C y dibujar en la parte superior de un centavo. Pero este ya es el momento de la optimización del algoritmo, y está más allá del alcance de este artículo.

Eso es todo lo que me gustaría decir. Puede encontrar una versión funcional del programa aquí: enlace github

1. En el archivo init.h, configure COINS_NUMBER - el número de denominaciones de monedas, y AMOUNT - la cantidad de cambio.
2. En el archivo coinc.c especifique las denominaciones de monedas en la matriz de monedas.
3. En Linux, ejecute make_sh.
4. Ejecute el programa de aplicación para su ejecución


Déjame darte un ejemplo divertido. Imagine que en algún país los matemáticos llegaron al poder y pusieron en circulación 32 denominaciones de monedas: 2, 3, 5, 7, 11, 13, 17, 19 ... 131. Para la conveniencia de contar, solo se eligieron números primos (bueno, ¿no es gracioso? ?) Y para asegurarse de que la reforma monetaria fue exitosa, enviaron un mensajero en la tienda del mensajero para intercambiar una factura 5333 (también un número primo). El cajero de una solución antigua de un solo núcleo resolvió el problema: 39 monedas con un valor nominal de 131 Pitágoras, una moneda 127 y una 97. El cálculo tomó 3 segundos y un poco más de un megabyte de memoria. El gobierno fue informado de que la gente está satisfecha con la reforma, cree rápidamente.


Y un ejemplo que es un poco más difícil de verificar. Monedas, cien denominaciones en una secuencia tan extraña: 0101, 0202, 0303 ... 9898, 9999, 100100. Cantidad de cambio: 101010. La búsqueda de una solución tomó 1 segundo y un poco más de un megabyte de memoria. Pero la decisión, de hecho, no es, es decir, es imposible recolectar tal cantidad con tales monedas. Con las mismas monedas, un cheque de 1 millón tomará 26 megabytes y cientos de segundos, lo que indica una dependencia exponencial de la cantidad, pero no del número de denominaciones de monedas.